LoginSignup
5
3
天文学Advent Calendar 2019Day 9
@phyblas(雛星 φυβλας)

非負値行列因子分解（NMF）で、星周円盤探索

Last updated at Posted at 2019-10-19

はじめに

この前は系外惑星探索について説明しました。
https://qiita.com/phyblas/items/52dc1bd113aff3745a8d

そして機械学習の技術である主成分分析（PCA）をこれに使う方法も紹介しました。
https://qiita.com/phyblas/items/84e35629f7c308128f1c

今回はPCAと同じく機械学習でよく使う特徴量抽出方法である非負値行列因子分解（NMF、non-negative matrix factorization）を使います。

ただし、今回の目標は系外惑星ではなく、星周円盤（circumstellar disc）にします。

星周円盤は、恒星の周りに円盤の姿に集まっている物質で、ガスや塵や微惑星や小惑星やその他、色々なものからできています。

若い恒星には原始惑星系円盤（protoplanetary disk）が、主系列星には残骸円盤（debris disks）があります。

惑星と同じように、恒星からの光が写っているため姿は見えるが、恒星と比べたら暗いものなので、惑星と同じようにADIの方法を使って観測することが多いです。

詳しくはwikipediaを参考に。

非負値行列因子分解（NMF）とは

qiitaにもにNMFに関する記事が充実なので、参考になれる記事を紹介する姿で、NMFの説明は省略します。

この記事ではNMFの概念と簡単なpythonでの実装方法（sklearnなしでnumpyで0から）
https://qiita.com/sumita_v09/items/d22850f41257d07c45ea

NMFの概念とsklearnでの実装はこれらの記事がいいです。
https://qiita.com/mamika311/items/d920be626c343bcb423a
https://qiita.com/mine820/items/3d0c261192d51b87d95e

この記事はNMFの概念の説明だけでなく、例としてラーメンの人気度を予測することにNMFを使う方法も紹介されます。
https://qiita.com/ogi-iii/items/fa0e9f244c9e35daab02

この記事はNMFとK-meansとの比較。（意外と比べられるものでした）
https://qiita.com/Riku-Sasaki/items/c1fb5e3669055c4b6716

NMFの使うところ

実はNMFの使い方と使うところはほぼこの前の記事で紹介したPCAと同じなので、ここでは色々なところは省略します。

任彬等(ren et al. 2018)の研究によると、円盤の観測の場合はPCA（KLIP）よりもNMFを使う方が円盤の姿がよく保たれるそうです。

なので、今回はPCAではなく、NMFで星周円盤の姿を明かそうとします。

使うデータ

今回で使うデータはこの前と同じくVLT（Very Large Telescope）のSPHEREのIRDISによって撮影された恒星の写真です。

データはこのサイトからダウンロード http://archive.eso.org/eso/eso_archive_main.html

SPHERE/IRDISのデータでは円盤を持っている星がたくさんありますが、自分でデータをダウンロードして処理してみたら、円盤の姿がよく見えるのは

円盤のある星の情報はこのサイトから検索できます
https://webdisks.jpl.nasa.gov/index.php

例としてここではまずHD141569を使います。他の結果も下に置いてあります。

系外惑星探索の紹介する記事と同じ方法で行きます。

まずはastroqueryで、使えるデータを検索します。

from astroquery.eso import Eso

eso = Eso()
eso.ROW_LIMIT = 10000
cf = {
    'target': 'HD141569',
    'dp_type': 'OBJECT',
    'dp_tech': 'IMAGE%',
    'seq_arm': 'IRDIS'
}
df = eso.query_instrument('sphere',column_filters=cf).to_pandas()
df = df.set_index('DP.ID')
print(df)

結果

                              Release Date  ... DIMM Seeing-avg
DP.ID                                       ...                
SPHER.2015-05-16T04:12:03.063   2017-05-16  ...     0.74 [0.01]
SPHER.2015-05-16T04:16:30.784   2017-05-16  ...     0.77 [0.01]
SPHER.2015-05-16T04:20:59.439   2017-05-16  ...     0.81 [0.01]
SPHER.2015-05-16T04:25:25.567   2017-05-16  ...     0.72 [0.01]
SPHER.2015-05-16T04:29:50.785   2017-05-16  ...     0.79 [0.01]
                                   ...  ...             ...
SPHER.2017-06-16T03:07:14.386   2019-06-16  ...     0.49 [0.01]
SPHER.2017-06-16T03:13:46.391   2019-06-16  ...     0.47 [0.01]
SPHER.2017-06-16T03:20:18.388   2019-06-16  ...     0.42 [0.01]
SPHER.2017-06-16T03:26:50.488   2019-06-16  ...     0.39 [0.01]
SPHER.2017-06-16T03:33:21.708   2019-06-16  ...     0.42 [0.01]

[129 rows x 33 columns]

SPHEREのデータの中にはHD141569が色々ありますが、今回は2015-05-16のデータを使うことにします。

サイトにログインしてretrieve_data()を使ってDP.IDを入力してダウンロードすることができます。

eso.login('ユーザー名', store_password=True)
data = eso.retrieve_data(['SPHER.2015-05-16T04:12:03.063'],destination='保存するフォルダ',with_calib='raw')

それとも、http://archive.eso.org/cms/eso-data/eso-data-direct-retrieval.html でDP.IDを入力してダウンロードするのです。

截屏2019-10-19上午10.00.49.png

ダウンロードしたら解凍してfitsファイルの中身を調べます。

from astropy.io import fits
import pandas as pd
from glob import glob1
import os

fd = 'データが保存されているフォルダ'
dpr = pd.DataFrame(index=['type','x,y,n','露出時間'])
for f in sorted(glob1(fd,'SPH*.fits')):
    hd = fits.getheader(os.path.join(fd,f))
    dpr[f] = [hd['hierarch eso dpr type'],'%d,%d,%d'%(hd['naxis1'],hd['naxis2'],hd['naxis3']),hd['exptime']]
dpr = dpr.T
print(dpr)

                                               type         x,y,n 露出時間
SPHER.2015-05-16T04:06:34.391.fits    OBJECT,CENTER   2048,1024,2   64
SPHER.2015-05-16T04:09:24.888.fits    OBJECT,CENTER   2048,1024,2   64
SPHER.2015-05-16T04:12:03.063.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T04:16:30.784.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T04:20:59.439.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T04:25:25.567.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T04:29:50.785.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T04:34:16.007.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T04:38:41.349.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T04:43:07.100.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T04:47:32.459.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T04:51:56.611.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T04:56:21.757.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T05:00:47.008.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T05:05:12.217.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T05:09:37.420.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T05:14:02.677.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T05:18:27.868.fits           OBJECT   2048,1024,4   64
SPHER.2015-05-16T05:26:54.661.fits      OBJECT,FLUX  2048,1024,30    4
SPHER.2015-05-16T05:30:05.932.fits              SKY   2048,1024,1   64
SPHER.2015-05-16T05:31:25.078.fits              SKY   2048,1024,1   64
SPHER.2015-05-16T05:32:42.897.fits              SKY   2048,1024,1   64
SPHER.2015-05-16T10:20:56.973.fits     LAMP,DISTORT   2048,1024,1    1
SPHER.2015-05-16T10:28:44.682.fits             DARK   2048,1024,1    1
SPHER.2015-05-16T11:12:31.312.fits             DARK   2048,1024,1   64
SPHER.2015-05-16T11:37:45.388.fits             DARK   2048,1024,1   16
SPHER.2015-05-16T11:59:13.127.fits  DARK,BACKGROUND   2048,1024,1   64
SPHER.2015-05-16T12:31:05.187.fits        FLAT,LAMP   2048,1024,1    2
SPHER.2015-05-16T12:31:38.306.fits        FLAT,LAMP   2048,1024,1    4
SPHER.2015-05-16T12:35:20.180.fits        FLAT,LAMP   2048,1024,1    6
SPHER.2015-05-16T12:36:34.223.fits        FLAT,LAMP   2048,1024,1    8
SPHER.2015-05-16T12:39:58.817.fits        FLAT,LAMP   2048,1024,1   10
SPHER.2015-05-18T13:29:02.779.fits  DARK,BACKGROUND   2048,1024,1    1

生データが揃ったら次はrawフォルダに入れて、vltpfで解析します。

解析した後、productsフォルダに解析完了のデータが置かれます。この中のscience_cube.fitsとscience_parang.fitsを使います。

実装

流れを纏めると、

  • 中心の部分を除外
  • 画像データを二次元のnn行mm列の行列にする
  • 最低値をひいて全ての値からマイナスを無くす
  • 残る成分の数を指定して、NMFを行う
  • データを変換し残る成分だけでデータを再構成、それを元のデータからひく
  • 全ての画像を視差角によって回転し、最後に中央値を求める

実はほぼPCAと同じですが、PCAでは平均値を0にするのが条件であるのに対し、NMFの場合は全ての値はマイナスではないってことが条件です。

画像は明るさのデータなので基本的にマイナスがないはずですが、解析した後の画像は矯正によってマイナスになる部分があります。

なので、最低値をひいて全てをマイナスでない値にする必要があります。

それと、PCAと同じく、中心の部分を除外する方がいい結果になることもありますが、今回はその段階を省略します。

NMFの計算はsklearnを使います。

ここでまずは成分の数を4にします。

import numpy as np
import matplotlib.pyplot as plt
from astropy.visualization import ZScaleInterval,ImageNormalize
from astropy.io import fits
from sklearn.decomposition import NMF
from skimage.transform import rotate
import os

folder = 'HD-141569_2015-05-16/products/'
path_sc = os.path.join(folder,'science_cube.fits')
path_parang = os.path.join(folder,'science_parang.fits')
z = fits.getdata(path_sc)[0] # 画像データ
parang = fits.getdata(path_parang) # 視差角

z -= z.min() # 最低値をひく
shape = z.shape
z = z.reshape(shape[0],-1) # 二次元の画像を一次元に変形する
nmf = NMF(4)
zp = nmf.inverse_transform(nmf.fit_transform(z)) # データを変換し残る成分だけでデータを再構成
z -= zp # 再構成された結果を元のデータからひく
z = z.reshape(*shape) # データ形を二次元の画像に戻す

# 視差角による回転
for i,parang_i in enumerate(parang):
    z[i] = rotate(z[i],-parang_i,cval=np.nan)
res = np.median(z[:,150:-150,150:-150],0) # 中央値

# 結果を描く
plt.figure(figsize=[6,5])
norm = ImageNormalize(res,interval=ZScaleInterval())
plt.imshow(res,origin='bottom',norm=norm,cmap='magma')
plt.colorbar(pad=0.01,aspect=40)
plt.tight_layout()
plt.show()

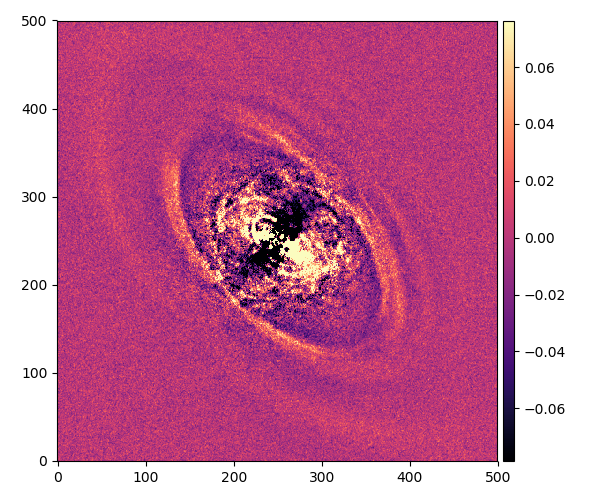
結果はこうなります。

HD141569_nmf04.png

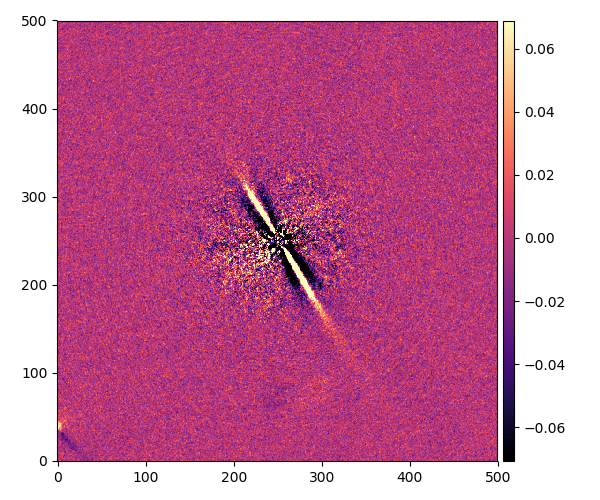
この星の円盤は地球から見れば角度は51°だからこんな風にちょうど綺麗に傾いているように見えます。

その他の結果

HD141569と同じ流れで、他の星もNMFを行うと円盤の姿が見えるものがあります。

使うデータセットは以下

星 データセット 露出時間 (秒) フレーム数 波長 (nm)
AU Mic SPHER.2016-06-04T07:32:34.958 16 320 1245/1245
HD 15115 SPHER.2015-10-29T04:36:26.900 16 192 1625/1625
HD 32297 SPHER.2016-12-19T03:19:45.454 64 56 1625/1625
HD 61005 SPHER.2015-03-30T00:11:47.635 64 64 2110/2251
HD 97048 SPHER.2016-03-28T02:02:54.758 64 80 1593/1667
HD 106906 SPHER.2015-05-09T01:05:58.831 16 256 1625/1625
HD 107146 SPHER.2016-03-19T04:37:10.292 16 160 1593/1667
HD 111520 SPHER.2016-05-15T01:45:56.568 32 128 1593/1667
HD 114082 SPHER.2017-05-17T02:00:14.618 64 96 1593/1667
HD 129590 SPHER.2016-05-04T04:06:43.971 32 80 1593/1667
HD 141569 SPHER.2015-05-16T04:12:03.063 32 56 1593/1667
HD 142527 SPHER.2016-06-14T02:22:54.969 0.8 3136 2110/2251
HIP 79977 SPHER.2017-04-29T05:45:51.542 64 80 2110/2251
KR Mus SPHER.2015-05-29T22:54:32.238 16 384 1593/1667
NZ Lup SPHER.2017-04-30T05:13:00.831 64 80 1593/1667
RX J1615.3-3255 SPHER.2015-05-15T05:19:25.602 64 64 1593/1667

成分の数の違いで結果は多少違うので、以下の結果は色んな値で試して、その中の一つだけ選んだのです。画像毎に使われた成分の数が違うのでそれぞれの使う数を表記します。

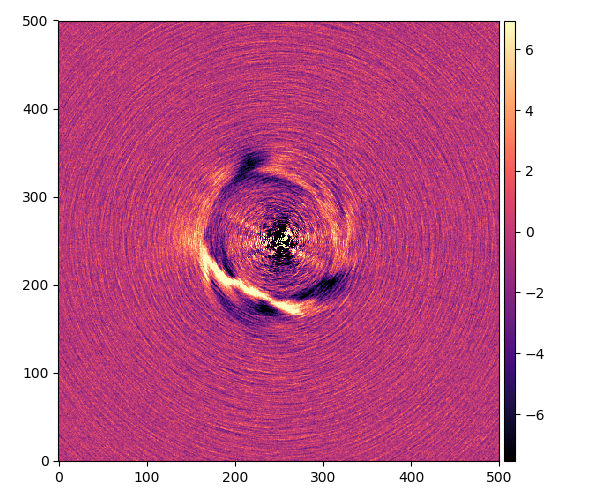
HD142527

成分の数：20
角度：30°

HD142527_nmf20.png

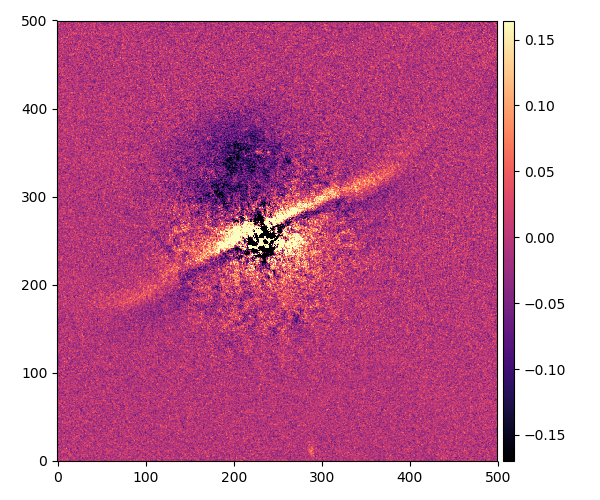
これは0.8という短い露出時間で3千枚以上撮ったデータ結果で、一番はっきりと円盤が見える星です。

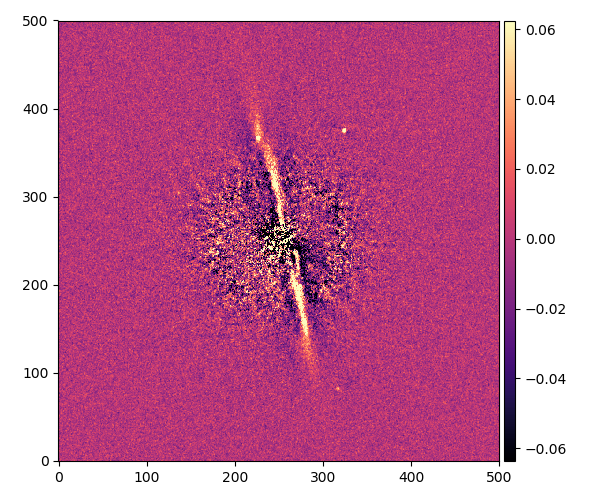
RXJ1615.3-3255

成分の数：4
角度：41°

RXJ1615.3-3255_nmf04.png

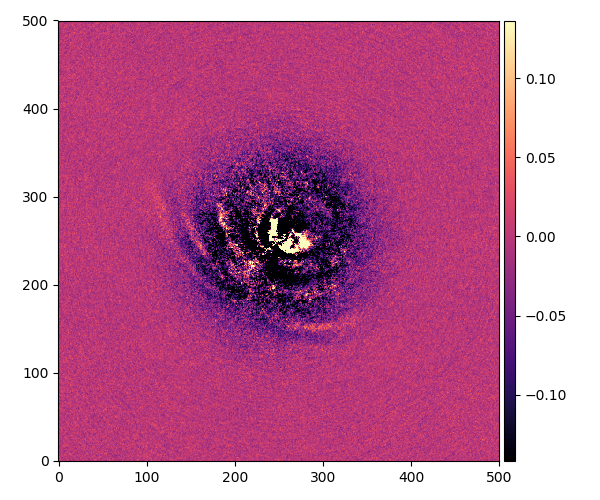
HD 97048

成分の数：2
角度：43°

HD97048_nmf02.png

これはちょっと見えにくいが、成分の数が少ないほうがはっきり見えます。

はえ座KR星（HD 100546）

成分の数：8
角度：43°

HD100546_nmf51.png

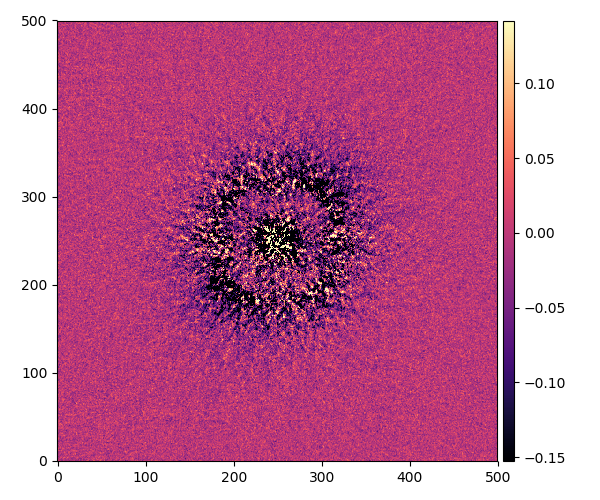
HD107146

成分の数：19
角度：18°

HD107146_nmf19.png

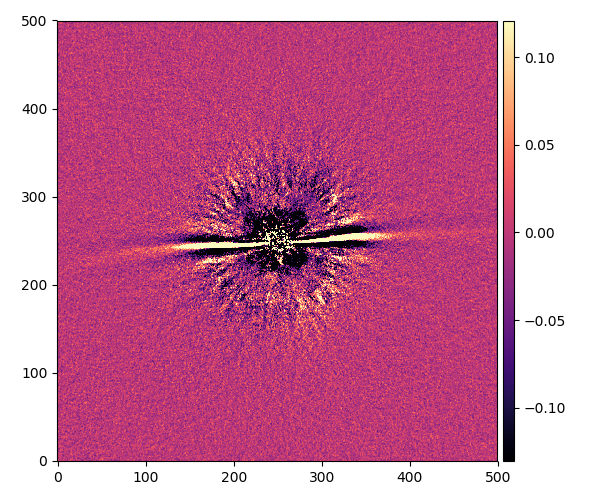
この星の円盤は角度が18°だからほぼ正面から見ているということです。こう見ると内側と外側の円盤がはっきり見えます。その中間は暗く見えます。

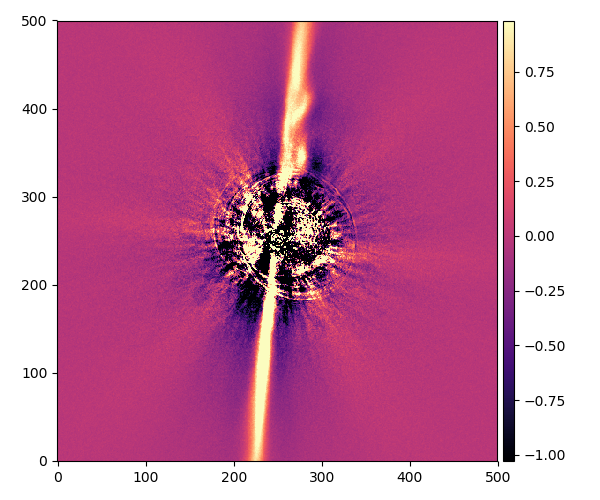
けんびきょう座AU星（HD 197481）

成分の数：11
角度：90°

AU Mic_nmf11.png

この星の円盤の角度は90°だから。ただの棒のように見えますね。

HD 15115

成分の数：13
角度：80°

HD15115_nmf13.png

HD 32297

成分の数：13
角度：90°

HD32297_nmf13.png

HD 61005

成分の数：4
角度：85°

HD61005_nmf04.png

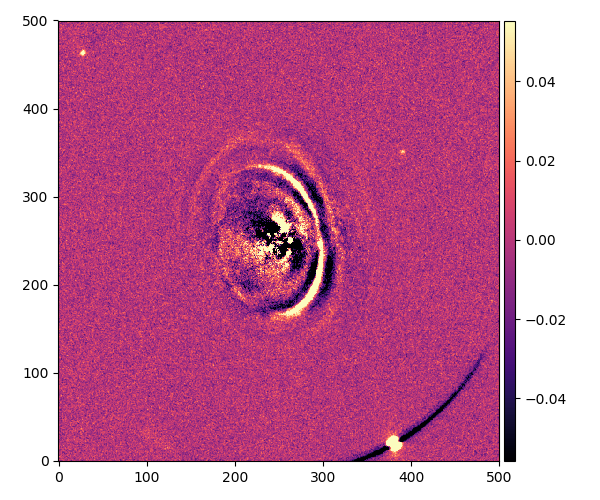
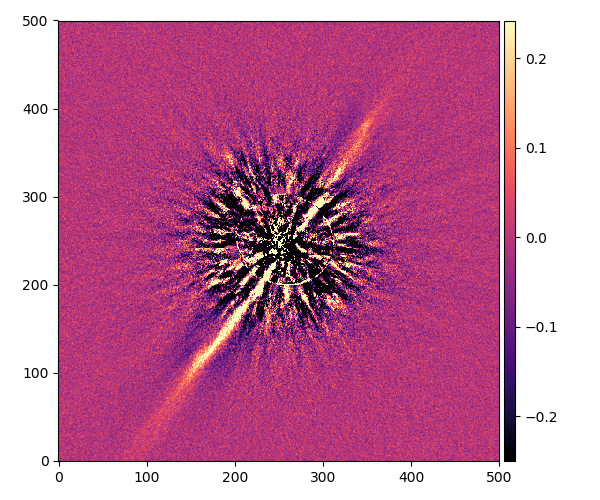
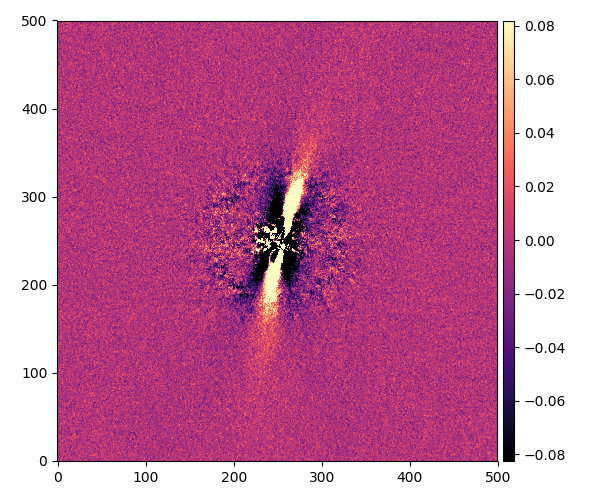
HD 114082　

成分の数：3
角度：83°

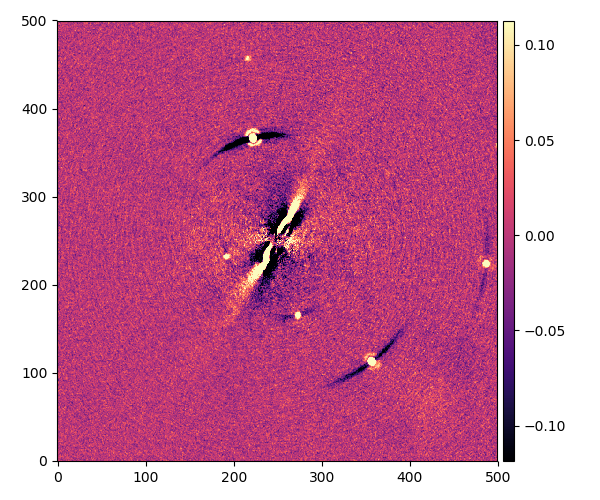
HD114082_nmf03.png

周りに小さな星がたくさん見えますが、これは惑星ではなく、遠く背景にある恒星です。

HD 111520

成分の数：6
角度：88°

HD111520_nmf06.png

HD129590

成分の数：8
角度：74.56°

HD129590_nmf08.png

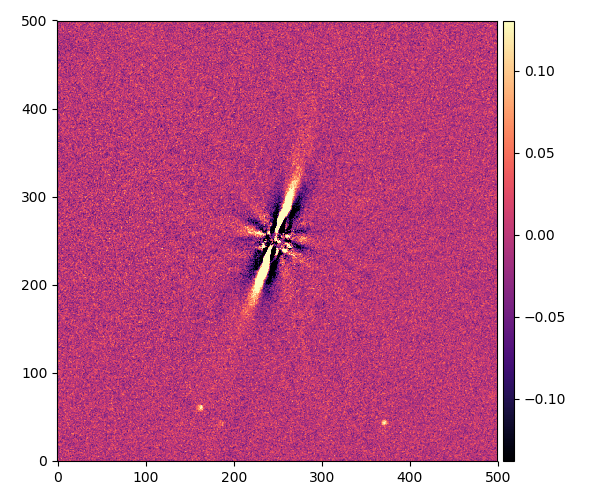
HIP 79977

成分の数：7
角度：84°

HD146897_nmf07.png

背景にある星は2つあります。

おおかみ座NZ星（HD 141943）

成分の数：10
角度：85°

NZ Lup_nmf10.png

終わりに

以上はADIにNMFを使って円盤の姿を捉える方法でした。

大体は円盤の角度が90°に近いものが多いから、円盤というより鉄亜鈴の姿のように見えるかもしれません。これの方が目撃しやすいから。

これらのデータセットにNMFの代わりにPCAを行っても似ているような結果ができるはずですが、NMFを使う方が円盤の姿がはっきり見えるようです。

5
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
5
3