みなさん、NMF(Non-negative Matrix Factorization:非負値行列因子分解)って知ってますか?
知ってましたか...では、何に使ってますか?
今回、とあるシーンで使ってみたところ、意外と使えました。
でもやっぱり目で見て感動したかったので、画像の分解で使ってみました。
NMFとは
アチラコチラで説明はいっぱい書かれていますので、詳しい解説は省略します。
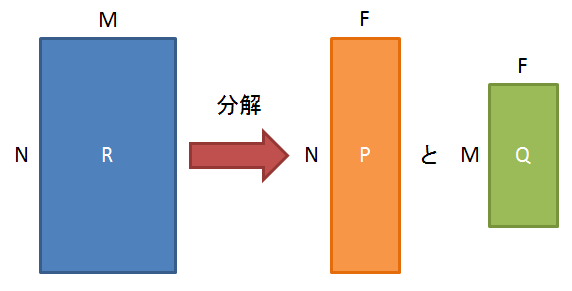
ざっくりとした説明ですが、ある行列を2つの行列に分解します。
このとき、分解される行列をR(MxNの行列)とし、分解後の2つの行列をP(FxNの行列)とQ(FxMの行列)とします。
このとき、「F」が分割数になり、いわゆる「特徴」を表すことになります。
「次元圧縮」とも言われたりします。
でも、数学をやっている人的には違和感がある図ですので、ちゃんと式にしてみます。
R \approx P \times Q^{T}
※実際には正確に分解できるわけではないので、「=」にはなりません
画像に適用すると?
これを画像に使ってみます。
といっても、Rは一枚の画像を表すわけではなく、複数枚の画像を表します。
つまり画像を2次元から1次元に変換し、画像枚数で2次元化します。
例えばMNISTの場合だと、28x28の画像ですので784になり、これを60,000枚使ったとすると、行列Rは
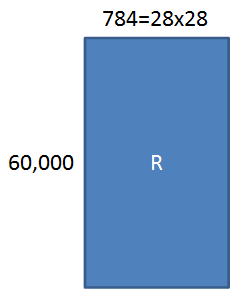
となります。
これを使ってNMFを実行すると、Pはどうでもいいとして、Qには60,000枚の画像データを学習して抽出したF枚の「特徴画像」が出来上がります。
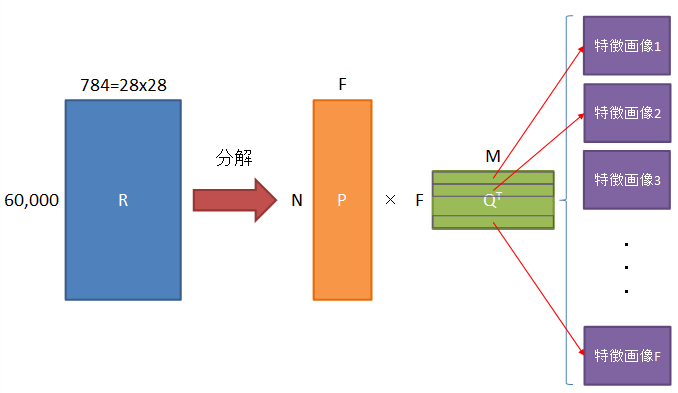
今回はそれを眺めて感動(笑)したいと思います。
MNISTで試してみる
MNISTとは...はいいですね ^^;
0~9の手書き文字のデータセットです。
ちなみに、開発・実行はJupyter Notebook上で行っています。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import NMF
import keras
from keras.datasets import mnist
まずはこんな感じでモジュールを読み込みます。
MNISTデータはkerasで読み込み、NMFはscikit-learnを使いたいと思います。
特徴画像はmatplotlibで表示します。
# MNISTデータの取得
(x_train, _), (_, _) = mnist.load_data()
x_train = x_train.reshape(-1, 784) # 2次元配列を1次元に変換
x_train = x_train.astype('float32') # int型をfloat32型に変換
x_train /= 255 # [0-255]の値を[0.0-1.0]に変換
print(x_train.shape[0], 'train samples')
MNISTデータを読み込みます。
テスト用とかカテゴリとかはいらないので読み込みません。
また、numpy配列にしてから、0.0~1.0に変換しています。
# 分解数
n_components = 4
# 分解
model = NMF(n_components=n_components, init='random', random_state=0) # n_componentsで特徴の次元を指定
P = model.fit_transform(x_train) # 学習
Q = model.components_
NMFで分解します。
とりあえずここでは4つに分解してみました。
最後の「Q」を使用します。
# 28x28の画像に変換
Q_image = Q.reshape(n_components, 28, 28)
# 画像の表示
fig = plt.figure(figsize=(18, 12))
for i in range(0, n_components):
ax = fig.add_subplot(1, n_components, i+1)
ax.imshow(Q_image[i])
plt.show()
Qを28x28になおして、画像を表示してみると、こうなりました。
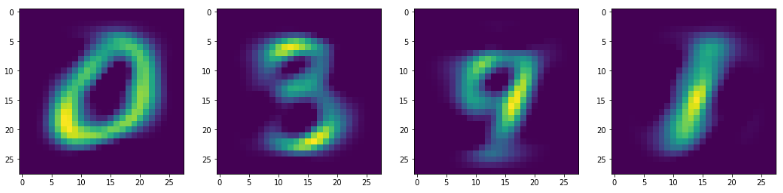
0~9の数字は、「0」「3」「9」「1」で表せるようです(嘘)
正直、もうちょっとぐちゃぐちゃな画像になるかと思ったので、意外でした。
もっと試してみる
では「10個に分割したら、ちゃんと0~9になるんじゃね?」ということで、試してみました。

世の中、そんなに甘くはないです。
もっと別の特徴を見つけ出してくれたようです。
ということは、10進法はベストな数字の分割数ではないのかもしれませんね...
※形状だけでのお話ですが ( ̄ー ̄)ニヤリ
そんな中でも、「3」「6」「7」「9」あたりは特徴的な形状のようです。
使ってみての感想
非常に簡単に特徴抽出できるのは嬉しいのですが、固定値で分割数を指定しなくてはいけないのが、ちょっと気持ち悪いですね~