Go to Qiita Advent Calendar Top
LoginSignup
1
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@phyblas(雛星 pʰyblas)

MATLABスクリプトで実行するSimulink入門

Last updated at Posted at 2025-11-06

この記事では、MATLABスクリプトを使用してGUI操作を介さずに直接Simulinkモデルを作成・実行する方法について説明します。

はじめに

最近制御工学に興味を持ち、関連する記事も執筆しました。

普段はPythonを使用しており、それで十分便利なのですが、複雑な制御モデルを構築する際には、GUI操作でブロック線図を確認しながら作成する方が簡単です。

そのような用途に適したツールがSimulinkです。Simulinkは様々なシステムのモデリングによく使用され、制御工学の業界では圧倒的な人気を誇っています。

Simulinkモデルを作成する方法には、直接GUIを操作する方法と、MATLABスクリプトで操作する方法があります。本記事で紹介するのは後者です。

この記事ではSimulink操作のための関数について説明しますが、配列やグラフなどMATLABの基礎知識については割愛します。

MATLABの入門記事も以前執筆しているので、そちらも参考にしていただければと思います。

今回の例で使用する制御システム

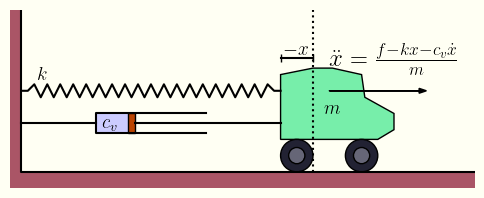
今回の例として実装したいのは、バネとダンパーが取り付けられた車の運動モデルです。これは制御工学の基礎でよく用いられるため、多くの方に馴染みがあるでしょう。

詳細については伝達関数の記事を参照してください。ここでは方程式のみを取り出して使用します。

運動方程式は以下の通りです。

m\ddot{x}(t) = f(t) - kx(t) - c\dot{x}(t)

これをラプラス変換すると、次の伝達関数が得られます。

G(s) = \frac{1}{ms^2 + cs + k}

簡単なサンプルコード

まず、以下のコードをMATLABで実行してみましょう。予めSimulinkを起動しておく必要がありません。詳細は後ほど説明します。

% 必要な変数を定義
m = 1;   % 質量
c = 0.2; % 粘性減衰係数
k = 1;   % バネ定数

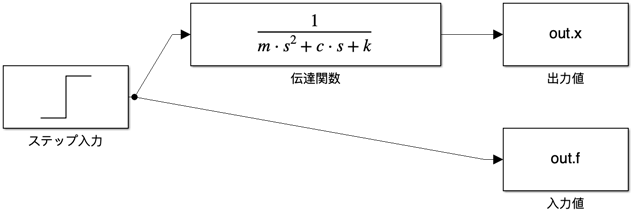
new_system('simo1') % モデル作成
open_system('simo1') % モデルのGUIウィンドウを開く

% モデルのソルバーに関するパラメーターを設定
set_param('simo1', ...
    StopTime='50', ...
    Solver='ode1', ...
    FixedStep='0.01')

% ステップ入力ブロックを追加
add_block('simulink/Sources/Step', ...
    'simo1/ステップ入力', ...
    Position=[50 100 150 150], ...
    Time='2', ...
    After='5')

% 伝達関数ブロックを追加
add_block('simulink/Continuous/Transfer Fcn', ...
    'simo1/伝達関数', ...
    Position=[200 50 400 100], ...
    Denominator='[m c k]')

% 力の値を出力するブロックを追加
add_block('simulink/Sinks/To Workspace', ...
    'simo1/入力値', ...
    Position=[450 150 550 200], ...
    SaveFormat='Array', ...
    VariableName='f')

% 位置の値を出力するブロックを追加
add_block('simulink/Sinks/To Workspace', ...
    'simo1/出力値', ...
    Position=[450 50 550 100], ...
    SaveFormat='Array', ...
    VariableName='x')

% 各ブロックを線で接続
add_line('simo1', 'ステップ入力/1', '伝達関数/1')
add_line('simo1', 'ステップ入力/1', '入力値/1')
add_line('simo1', '伝達関数/1', '出力値/1')

% モデルを実行して結果を取得
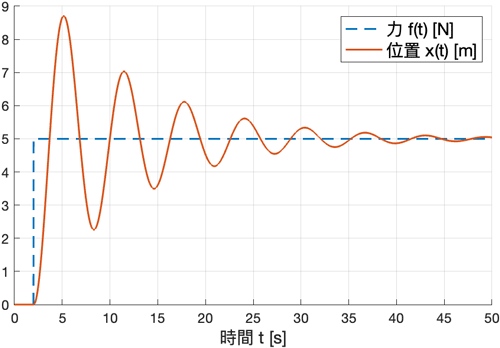
sout = sim('simo1');

% 結果をグラフ表示
figure(Position=[100 100 500 300])
hold on
plot(sout.tout, sout.f, DisplayName='力 f(t) [N]', LineWidth=1.5, LineStyle='--')
plot(sout.tout, sout.x, DisplayName='位置 x(t) [m]', LineWidth=1.5)
xlabel('時間 t [s]', FontSize=14)
legend(FontSize=14)
grid

save_system('simo1') % モデルを保存

実行すると、SimulinkのGUI内に以下のような4つのブロックで構成されたシンプルなモデルが作成されます。

qsimo01.png

結果のグラフは以下のように描画され、予想通りの減衰振動が確認できます。

qsimo02.png

Simulinkモデルの設計は自由度が高く自由に行えますが、業務で使用する際はガイドラインに従う必要がある場合が殆どです。例えば日本の自動車業界ではJMAABの基準（Japan MATLAB Automotive Advisory Board）が存在します。

今回の例のようにブロック名を日本語にすることはJMAABでは推奨されていません。不具合の原因となりやすいため、通常はASCII文字のみを使用します。

ただし今回は学習用として分かりやすくするため、ブロック名を日本語にしています。個人利用の場合は自由に設定して構いません。

よく使う主な関数の説明

new_system

まずnew_system関数で新しい空のモデルを作成します。モデル名のみを指定すればよく、この名前は後続の操作で使用するため重要です。既に同じ名前のモデルが開いている場合はエラーになります。名前を指定しない場合、自動的に「untitled」という名前になります。

この関数の戻り値は「数値ハンドル」と呼ばれる浮動小数点数です。

h = new_system('hoge');
h % 152.0391 など

後でモデルを操作する際にこの数値を使用することもできますが、今回は分かりやすさのためモデル名を使用します。

open_system

new_systemで作成したモデルはすぐには表示されません。モデルウィンドウを開くにはopen_system関数を使用する必要があります。モデル名又は数値ハンドルを指定します。

又、この関数は保存済みのモデルを開くためにも使用します。

後述するload_system関数と似ており混同しやすいですが、違いについてはload_systemの項で説明します。

set_param

次にパラメーターを設定します。ここでset_param関数を使用します。今回の例ではソルバー関連のパラメーターのみ設定しましたが、Simulinkモデルには他にも多数のパラメーターがあります。

・StopTime='50'：50秒までシミュレーション
・Solver='ode1'：ソルバーにode1（単純なオイラー法）を指定
・FixedStep='0.01'：固定ステップ0.01秒で計算

ソルバーのデフォルトは可変ステップですが、仕様が複雑で不具合の原因となりやすいため、通常は固定ステップのode1（オイラー法）、ode2（台形公式）、ode4（ルンゲ＝クッタ法）が一般的です。

又、この関数はモデルのパラメーター設定だけでなく、ブロックやサブシステムなどの設定にも使用します。使用例は後述します。

get_param

set_paramがあるため、パラメーター値を取得するget_paramも当然存在します。

例えば、シミュレーション開始時間とソルバーの種類を取得します。

start_time = get_param('simo1', 'StartTime') % '0.0'
solver_type = get_param('simo1', 'SolverType') % 'Fixed-step'

今回の例ではソルバーをode1に設定したため、ソルバーの種類は自動的に固定ステップになります。

又、ObjectParametersパラメーターにはオブジェクトの全パラメーター名が含まれるため、存在するパラメーターを確認したい場合はこれを調べることもできます。

param_list = get_param('simo1', 'ObjectParameters')

add_block

new_systemでモデルを作成すると最初は空のモデルが表示されますが、その後ブロックを追加していきます。ブロックの追加にはadd_blockを使用します。

使用方法

add_block(ソース, 絶対パス, パラメーター1, パラメーター2, ...)

ソースは追加するブロックの種類です。例えば今回使用したのは以下の3つです。

  • Step（simulink/Sources/Step）：ステップ関数の入力を生成するブロック
  • TransferFcn（simulink/Continuous/Transfer Fcn）：伝達関数ブロック
  • ToWorkspace（simulink/Sinks/To Workspace）：値をワークスペースに出力するブロック

絶対パスはモデル名/ブロック名の形式で、モデル名とそのブロック自身の名前を含みます。これは後でこのブロックを参照する際に使用されるため重要です。

パラメーター設定は同時に行うことも、後でset_param関数を使用して設定することもできます。例えば：

set_param('simo1/ステップ入力', Time='2')

ただし、ブロックのパラメーターは文字列として指定する必要がある場合が多いです。数値や配列であっても同様です。ただしPositionなどは直接配列として指定できるため注意が必要です。

Positionの指定は[左 上 右 下]の座標です。

TransferFcnブロックにDenominator='[m c k]'を指定すると、分母が$ms^2 + cs + k$になります。ここで変数m、c、kはワークスペースの変数を使用するため、事前に定義する必要があります。分子はNumeratorパラメーターですが、デフォルトは[1]であるため今回は設定不要です。

add_line

ブロック間を接続する線を追加するにはadd_line関数を使用します。

使用方法

add_line(モデル名, 出力, 入力)

出力と入力はブロック名/ポート番号の形式で指定します。ポートが1つのみの場合は/1を指定します。

線は指定した出力と入力の間に引かれます。

これでモデル自体は完成です。次はモデルの実行です。

sim

Simulinkモデルを実行するにはsim関数を使用します。この関数には様々な使用方法がありますが、まずは最も簡単な使用方法を紹介します。実行したいモデル名を指定するだけです。

sout = sim('simo1');

戻り値にはシミュレーション結果の各種データが含まれます。

sout = 

  Simulink.SimulationOutput:

                      f: [5001x1 double] 
                   tout: [5001x1 double] 
                      x: [5001x1 double] 

     SimulationMetadata: [1x1 Simulink.SimulationMetadata] 
           ErrorMessage: [0x0 char]

デフォルトでは.toutにシミュレーション時間の配列が格納されます。今回は0.01秒ステップで0-50秒のため、長さ5001になります。その他にToWorkspaceブロックで指定した出力の種類があります。今回はSaveFormat='Array'にしたため、できる値も配列になっていますが、デフォルトではtimeseries（時系列）オブジェクトです。これについては後述しますが、今回の例では配列の方が扱いやすいです。

結果を使用してグラフを描画したり、保存したりすることができます。

又、戻り値を取得しなくても、実行後にoutという変数に同じシミュレーション結果が格納されているはずです。ただしこれはモデル設定によって異なるため、戻り値を使用する方が安全です。

この例では単純にモデルをそのまま実行しましたが、simのより複雑な使用方法については後述します。

save_system

モデルをファイルとして保存するにはsave_system関数を使用します。基本的にモデル名を指定するだけで、ファイルには拡張子.slxが付きます。

別の名前で保存する場合は以下のようにします。

save_system(モデル名, 新しいモデル名)

ただし、この場合モデル名も変更され、元の名前では使用できなくなるため、以降は新しい名前を使用する必要があります。

モデル名とファイル名は基本的に一致します。

これでサンプルコードで使用した関数の説明は完了です。他にも関連する関数が多数あるため、引き続き紹介します。

close_system

close_systemは使用しないモデルを閉じるために使用します。

使用方法は、閉じたいモデル名を指定するだけです。ただし、モデルが変更され保存されていない場合、エラーが発生します。その場合は第2引数に0を指定することで保存せずに閉じることができます。

close_system(モデル名, 0)

一方、保存してから閉じたい場合は1を指定します。

close_system(モデル名, 1)

別の名前で保存したい場合はその名前を指定することもできます。

close_system(モデル名, モデルの新しい名前)

close_systemでモデルを閉じることは、モデルGUIウィンドウを手動で閉じるのとほぼ同じです。ただし、ウィンドウが表示されていないモデルもclose_systemで閉じることができます。

GUIウィンドウ自体は表示されていないが実際には開いているモデルは、主にopen_systemを使用せずnew_systemで作成したモデルや、次に紹介するload_system関数で開いた場合です。

load_system

load_systemはファイルに保存されたモデルを開くために使用します。ただしGUIウィンドウは表示されません。

open_systemでもファイルからモデルを読み込むことができますが、open_systemは同時にGUIウィンドウを開きます。

モデルを実行して結果を取得するだけならGUIウィンドウは不要なため、open_systemよりもload_systemを使用した方が高速です。

ただし使用後はclose_systemで閉じる必要があります。

find_system

モデル内のコンポーネントを検索するにはfind_systemを使用します。戻り値は該当する全ての絶対パスのcell配列です。使用方法は様々です。例えば指定した種類のブロックを検索したい場合はBlockTypeを使用します。

find_system('simo1', BlockType='ToWorkspace')

結果

    {'simo1/入力値'}
    {'simo1/出力値'}

ブロック名（モデル名を含まない）から検索することもできます。

find_system('simo1', Name='伝達関数')

結果

    {'simo1/伝達関数'}

モデル名のみを指定すると、そのモデルを含む全てのブロックが返されます。

find_system('simo1')

結果

    {'simo1'           }
    {'simo1/ステップ入力'}
    {'simo1/伝達関数'   }
    {'simo1/入力値'     }
    {'simo1/出力値'     }

gcb

gcb（get current blockの略）関数は最後に操作したブロックの絶対パスを返します。

gcb % 'simo1/出力値'

delete_block

delete_block関数は指定した絶対パスのブロックを削除します。cell配列を指定すると複数削除できます。

例えば全てのブロックを削除したい場合は以下のようにします。

delete_block(find_system('simo1', Type='block'))

delete_line

delete_line関数で線を削除できます。

ただし線には通常名前がないため、削除する際は接続されている2つのブロック名を使用します。入力方法はほぼadd_lineと同じです。例えば：

delete_line('simo1', 'ステップ入力/1', '伝達関数/1')

ただし、両端がブロックに接続されていない線はこの方法では削除できません。代わりに線が配置されている点を指定して削除することもできます。

片側のみ接続されている場合はget_param関数でPortConnectivity（入出力の接続）の値を取得して使用できます。

pcp = get_param('simo1/ステップ入力', 'PortConnectivity').Position;
pcp % 155   125
delete_line('simo1', pcp)

又は数値ハンドルを入力することもできます。この場合、複数削除できます。

例えば全ての線を削除したい場合は以下のようにします。

delete_line(find_system('simo1', findall='on', Type='line'))

尚、find_systemはデフォルトではモデル自身とブロックのみを返しますが、findall='on'を指定すると線も含まれます。この場合、戻り値は絶対パスではなく数値ハンドルになります。ここでType='line'を指定すると線のみに絞り込まれ、これをdelete_lineの入力として使用できます。

simulink.blockdiagram.arrangesystem

上述の例では各ブロックの位置を手動で指定しましたが、ブロック数が多いと面倒です。Positionを指定せずに追加すると適当な場所に配置され、わかりにくいことがあります。

この問題はsimulink.blockdiagram.arrangesystem関数を使用することで解決できます。この関数は自動的に適切な位置に配置し、分かりやすいレイアウトにします。

試しに上述の例のモデルに適用してみます。

Simulink.BlockDiagram.arrangeSystem('simo1')

すると以下のようになります。

qsimo03.png

実行の様々な設定

変更した設定でモデル実行

モデルを異なる設定で実行したい場合は、sim関数を呼び出す際に設定オブジェクトを指定できます。

まず使用例を示します。上述で作成したモデルを読み込み、設定を変更して実行します。

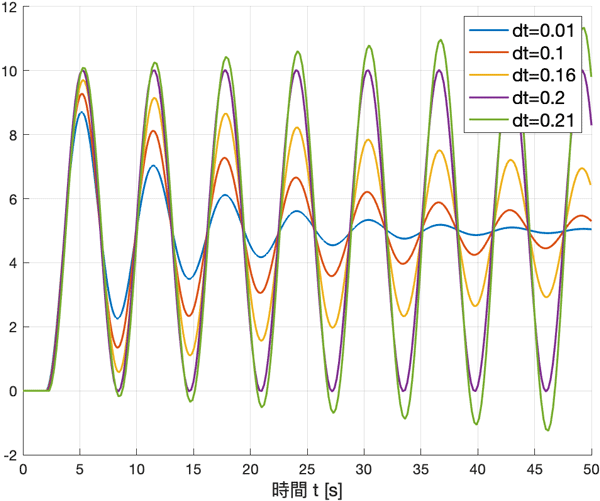
今回検証するのはステップ間隔の影響です。FixedStepパラメーターを変更しながら違いを比較します。

m = 1; c = 0.2; k = 1;
load_system('simo1')
config = copy(getActiveConfigSet('simo1'));

figure
hold on
for fs = [0.01 0.1 0.16 0.2 0.21]
    set_param(config, FixedStep=num2str(fs))
    sout = sim('simo1', config);
    plot(sout.tout, sout.x, DisplayName="dt="+fs, LineWidth=1.5)
end
xlabel('時間 t [s]', FontSize=14)
legend(FontSize=14)
grid
close_system('simo1')

qsimo04.png

同じモデルでも結果が全く異なりますね。もちろんステップ間隔が小さい方がより正確です。ステップが大きくなると誤差が大きくなり、最終的には減衰振動ではなく発散することさえあります。

尚、今回はload_systemを使用してウィンドウを開かずに実行しました。ただしこの場合、close_systemで閉じることを忘れないでください。

本題に戻ります。ここでgetActiveConfigSet関数を使用することで、そのモデルのSimulink.ConfigSetオブジェクトを取得できます。これをcopy関数でコピーし、set_param関数で一部設定を変更してsim関数に渡すと、今回のみ変更した設定でモデルを実行できます。

この場合、元のモデルの設定パラメーターは実際には変更されません。うっかりモデルを変更してしまう心配がなく便利です。ただしここでcopy関数を使用せずconfig = getActiveConfigSet('simo1');と記述すると、set_paramを使用した際にモデルの設定も実際に変更されるため注意が必要です。

又setModelParameterを使用する方法もあります。この方法については次の項目で合わせて説明します。

指定した変数でモデル実行

sim関数にはモデル名を指定する他に、Simulink.SimulationInputオブジェクトを指定することもできます。この方法を使用すると、様々なパラメーターや変数を設定変更した上で実行できます。

例えば上述のsetModelParameterを使用してモデルのパラメーターを変更できます。これによりワークスペースで定義した変数の代わりに使用されます。

その他にもsetVariableを使用してモデル内で使用される変数を設定できます。

いずれもその実行のみの設定であり、元のモデルや変数に影響はありません。

モデル内で変数を使用したい場合、寧ろこの方法をお勧めします。ワークスペースの変数は当該モデルの実行だけでなく他のモデルにも影響を与えるため、不具合の原因となりやすいからです。setVariableを使用して実行時のみの変数設定にすると安全に実行できます。

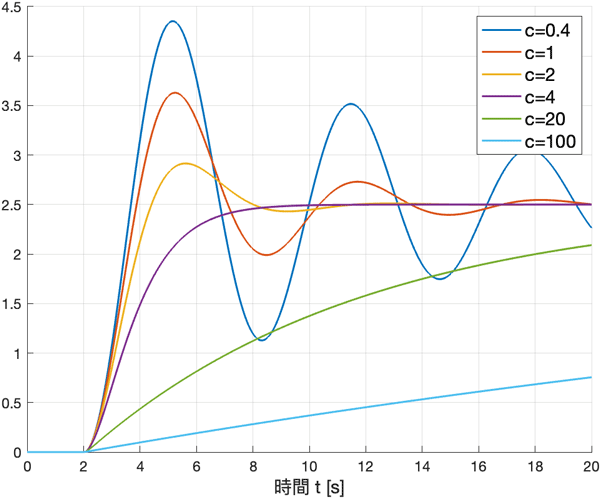
粘性減衰係数$c$を調整して結果を比較してみましょう。

load_system('simo1')
simin = Simulink.SimulationInput('simo1');
simin = setModelParameter(simin, StopTime='20');
simin = setVariable(simin, k=2);
simin = setVariable(simin, m=2);

figure
hold on
for c = [0.4 1 2 4 20 100]
    simin = setVariable(simin, c=c);
    sout = sim(simin);
    plot(sout.tout, sout.x, DisplayName="c="+c, LineWidth=1.5)
end
xlabel('時間 t [s]', FontSize=14)
legend(FontSize=14)
grid
close_system('simo1')

qsimo05.png

理論通り$c$が大きすぎると過減衰となり振動が見られなくなりますね。

パラメーターを更新したブロックでモデル実行

モデル設定のパラメーターはsetModelParameterを使用しますが、ブロック内のパラメーターを変更したい場合はsetBlockParameterを使用します。

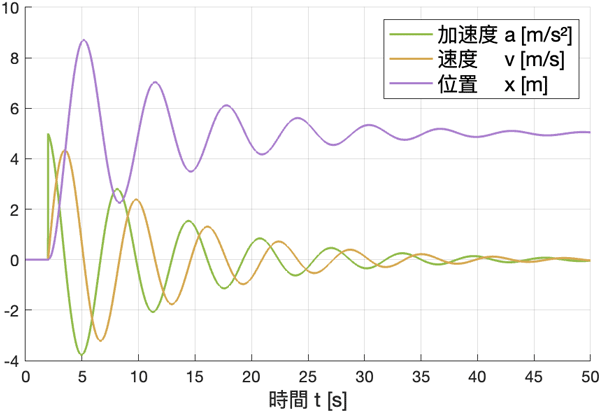
例えば上述のモデルの伝達関数$G(s) = \frac{1}{ms^2 + cs + k}$は位置を出力しますが、$s$を掛けて$G(s) = \frac{s}{ms^2 + cs + k}$とすると速度に、さらに$s$を掛けて$G(s) = \frac{s^2}{ms^2 + cs + k}$とすると加速度になります。

ではブロックの分子部分を少し変更し、加速度と速度を出力するように変更して実行してみましょう。

m = 1; c = 0.2; k = 1;
load_system('simo1')
simin = Simulink.SimulationInput('simo1');

figure(Position=[100 100 500 300])
hold on

% 加速度
simin = setBlockParameter(simin, 'simo1/伝達関数', Numerator='[1 0 0]');
simin = setBlockParameter(simin, 'simo1/出力値', VariableName='a');
sout = sim(simin);
plot(sout.tout, sout.a, DisplayName='加速度 a [m/s²]', LineWidth=1.5, Color='#93bc4d')

% 速度
simin = setBlockParameter(simin, 'simo1/伝達関数', Numerator='[1 0]');
simin = setBlockParameter(simin, 'simo1/出力値', VariableName='v');
sout = sim(simin);
plot(sout.tout, sout.v, DisplayName='速度　 v [m/s]', LineWidth=1.5, Color='#d6aa54')

% 又本来のモデルで実行して位置を得て一緒にグラフに入れる
sout = sim('simo1');
plot(sout.tout, sout.x, DisplayName='位置　 x [m]', LineWidth=1.5, Color='#ac82cf')

xlabel('時間 t [s]', FontSize=14)
grid
legend(FontSize=14)
close_system('simo1')

qsimo06.png

入力のInportと出力のOutport

上述の例ではモデル内で準備した入力を使用しましたが、Inport（simulink/Quick Insert/Ports & Subsystems/Inport）ブロックを使用すると外部から入力することもできます。

又、出力はToWorkspaceブロックの他にOutport（simulink/Quick Insert/Ports & Subsystems/Outport）ブロックを使用する方法もあります。

これら2つはよく併用されるため、合わせて使用例を示します。

上の例と似た伝達関数のモデルを作成しますが、今回は入出力にInportとOutportを使用します。

t = 0:0.2:14;
f = 20*sin(t); % 入力の力を正弦波にする
ft = timeseries(f, t, Name='f(t)'); % 時系列オブジェクトを作る
ft.DataInfo.Interpolation = 'zoh'; % 補間をゼロ次ホールドにする

new_system('simo2')
open_system('simo2')

set_param('simo2', ...
    StopTime='20', ...
    Solver='ode4', ...
    FixedStep='0.01')

add_block('simulink/Quick Insert/Ports & Subsystems/Inport', ...
    'simo2/入力')

add_block('simulink/Continuous/Transfer Fcn', ...
    'simo2/伝達関数', ...
    Position=[50 50 200 100], ...
    Denominator='[0.1 0.02 10]')

add_block('simulink/Quick Insert/Ports & Subsystems/Outport', ...
    'simo2/出力', ...
    SignalName='x(t)')

add_line('simo2', '入力/1', '伝達関数/1')
add_line('simo2', '伝達関数/1', '出力/1')

Simulink.BlockDiagram.arrangeSystem('simo2')

simin = Simulink.SimulationInput('simo2');
sida = Simulink.SimulationData.Dataset;
sida = sida.addElement(ft);
simin = setExternalInput(simin, sida);
% simin = setExternalInput(simin, ft); % 入力が1つのみの場合はこれでも可
sout = sim(simin);

figure(Position=[100 100 600 450])
tiledlayout(2, 1, TileSpacing='compact', Padding='compact')

nexttile
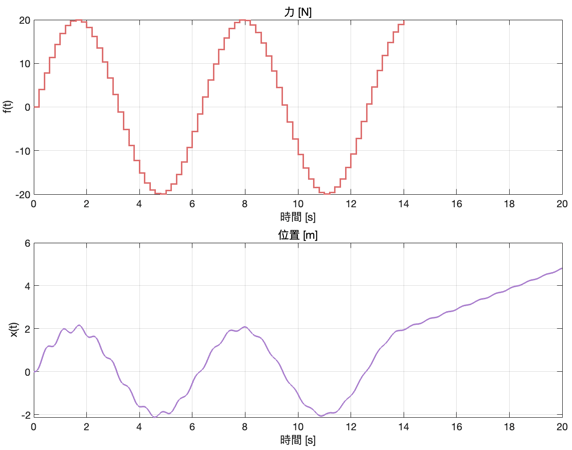
plot(ft, LineWidth=1.5, Color='#de7272')
title('力 [N]')
xlabel('時間 [s]')
xlim([0 20])
grid

nexttile
plot(sout.yout{1}.Values, LineWidth=1.5, Color='#ac82cf')
title('位置 [m]')
xlabel('時間 [s]')
xlim([0 20])
grid

実行すると、以下のようなシンプルなモデルが作成されます。

qsimo07.png

結果のグラフは以下の通りです。

qsimo08.png

Inportブロックへの入力データにはtimeseriesクラスを使用します。これは時系列データを扱うためのクラスです。Simulink内部で流れるデータは基本的に時系列形式です。Outportブロックからの出力も同様に時系列データとなります。ToWorkspaceブロックを使用する場合もデフォルトでは時系列形式ですが、SaveFormat='Array'を設定することで通常の配列形式に変換できます。

時系列データには、値そのものに加えて対応する時間情報も含まれています。

入力として使用する時系列データは、モデルのソルバー時間と完全に一致する必要はありません。Simulinkが適切に補間と外挿を行います。今回の例では入力データは14秒までですが、それ以降の値は自動的に外挿されました。

.DataInfo属性には追加情報が格納されています。例えば.DataInfo.Interpolationは補間方法を指定します。デフォルトはlinear（線形補間）ですが、zoh（ゼロ次ホールド）を指定すると段階的な定数値になります。この違いはグラフ描画時にも確認できます。

今回は

ft.DataInfo.Interpolation = 'zoh';

と設定しているため、ギザギザの入力波形になっています。

plot関数でグラフを描画する際、時系列オブジェクトを指定するだけで、時間がx軸、値がy軸として自動的にプロットされます。

時系列オブジェクトには名前を付けることができ、この名前はグラフのy軸ラベルとして表示されます。Outportブロックを使用する場合、SignalNameパラメーターで指定した名前が出力時系列の名前になります。

Inportブロックに入力値を入れる方法は少し面倒です。まずは時系列を作って、Simulink.SimulationData.Datasetオブジェクトに入れます。そしてaddElementメソッドで時系列を追加してからsetExternalInput関数でSimulink.SimulationInputに入れて、これをsim関数に入れて実行します。追加したい時系列が複数ある場合はただ次々とaddElementで追加するだけです。

ただし、入力が1つのみの場合は、Simulink.SimulationData.Datasetを使用せずに時系列オブジェクトを直接setExternalInputに渡すこともできます。今回の例では入力がftのみであるため、以下のように記述しても問題ありません。

simin = setExternalInput(simin, ft);

Outportからの出力は、ポート番号順に戻り値の.yout属性に格納されます。データはセル配列形式で格納されているため、{1}のようにしてアクセスします。ただし、ここに格納されている値はSimulink.SimulationData.Signalというデータ型です。.Values属性にアクセスすることで、時系列データを取得できます。そのため、今回は以下のようにして時系列データを取得しています。

sout.yout{1}.Values

サブシステム

サブシステムとは、モデル内のブロックをグループ化したものです。大規模で複雑なモデルを作成する場合、サブシステムに分割することで理解しやすくなります。

サブシステムもブロックの一種であるため、add_block関数で追加できます。ブロックの種類はSubSystem（simulink/Ports & Subsystems/Subsystem）です。追加後、その内部にブロックを配置することができます。

サブシステム内部のブロック操作は基本的にモデル内での操作と同じですが、絶対パスにはモデル名に加えてサブシステム名も含め、モデル名/サブシステム名/ブロック名という形式になります。

新しく作成されたサブシステムは空っぽではなく、常にInportブロックとOutportブロックが付属しています。

qsimo09.png

これらのInportとOutportブロックはモデルレベルのものと同じ種類ですが、サブシステム内ではそのサブシステムブロックの入力と出力となります。必要な数に応じてポートを追加することもできます。

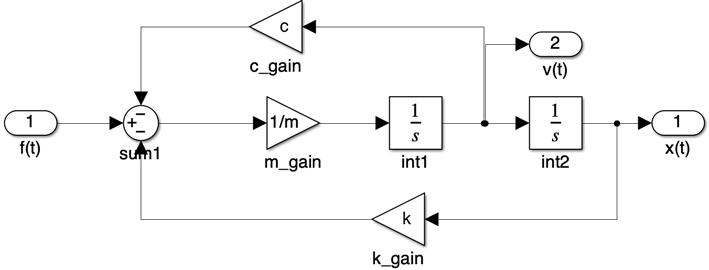
ここでサブシステムの使用例を紹介します。今回はTransferFcnブロックを使用せずに、バネとダンパーが付いた車のモデルをサブシステムとして作成します。

m = 8;
c = 20;
k = 200;

new_system('simo3')
open_system('simo3')

set_param('simo3', ...
    StopTime='50', ...
    Solver='ode2', ...
    FixedStep='0.05')

add_block('simulink/Ports & Subsystems/Subsystem', ...
    'simo3/サブシ', ...
    Position=[50 50 300 200])

add_block('simulink/Math Operations/Sum', ...
    'simo3/サブシ/sum1', ...
    IconShape='round', ...
    Inputs='-+-')

add_block('simulink/Math Operations/Gain', ...
    'simo3/サブシ/m_gain', ...
    Gain='1/m')

add_block('simulink/Math Operations/Gain', ...
    'simo3/サブシ/c_gain', ...
    Orientation='left', ...
    Gain='c')

add_block('simulink/Math Operations/Gain', ...
    'simo3/サブシ/k_gain', ...
    Orientation='left', ...
    Gain='k')

add_block('simulink/Continuous/Integrator', ...
    'simo3/サブシ/int1')

add_block('simulink/Continuous/Integrator', ...
    'simo3/サブシ/int2')

add_block('simulink/Quick Insert/Ports & Subsystems/Outport', ...
    'simo3/サブシ/v(t)')

inp1 = find_system('simo3/サブシ', BlockType='Inport');
set_param(inp1{1}, Name='f(t)')

outp1 = find_system('simo3/サブシ', BlockType='Outport');
set_param(outp1{1}, Name='x(t)')

delete_line('simo3/サブシ', 'f(t)/1', 'x(t)/1')

add_line('simo3/サブシ', 'f(t)/1', 'sum1/2')
add_line('simo3/サブシ', 'sum1/1', 'm_gain/1')
add_line('simo3/サブシ', 'm_gain/1', 'int1/1')
add_line('simo3/サブシ', 'int1/1', 'int2/1')
add_line('simo3/サブシ', 'int1/1', 'c_gain/1')
add_line('simo3/サブシ', 'c_gain/1', 'sum1/1')
add_line('simo3/サブシ', 'int2/1', 'k_gain/1')
add_line('simo3/サブシ', 'k_gain/1', 'sum1/3')
add_line('simo3/サブシ', 'int1/1', 'v(t)/1')
add_line('simo3/サブシ', 'int2/1', 'x(t)/1')

add_block('simulink/Sources/Pulse Generator', ...
    'simo3/パルス入力', ...
    Amplitude='240', ...
    Period='16', ...
    PulseWidth='50')

add_block('simulink/Sinks/To Workspace', ...
    'simo3/入力の力', ...
    SaveFormat='Array', ...
    VariableName='f')

add_block('simulink/Sinks/To Workspace', ...
    'simo3/出力の速度', ...
    SaveFormat='Array', ...
    VariableName='v')

add_block('simulink/Sinks/To Workspace', ...
    'simo3/出力の位置', ...
    SaveFormat='Array', ...
    VariableName='x')

add_line('simo3', 'パルス入力/1', 'サブシ/1')
add_line('simo3', 'パルス入力/1', '入力の力/1')
add_line('simo3', 'サブシ/1', '出力の位置/1')
add_line('simo3', 'サブシ/2', '出力の速度/1')

Simulink.BlockDiagram.arrangeSystem('simo3')
Simulink.BlockDiagram.arrangeSystem('simo3/サブシ')

sout = sim('simo3');

figure(Position=[100 100 600 600])
tiledlayout(3, 1, TileSpacing='compact', Padding='compact')
nexttile
plot(sout.tout, sout.f, LineWidth=1.5, Color='#de7272')
ylabel('力 f(t) [N]', FontSize=14)
xticklabels([])
grid
nexttile
plot(sout.tout, sout.v, LineWidth=1.5, Color='#d6aa54')
ylabel('速度 v(t) [m/s]', FontSize=14)
xticklabels([])
grid
nexttile
plot(sout.tout, sout.x, LineWidth=1.5, Color='#ac82cf')
ylabel('位置 x(t) [m]', FontSize=14)
xlabel('時間 t [s]', FontSize=14)
grid

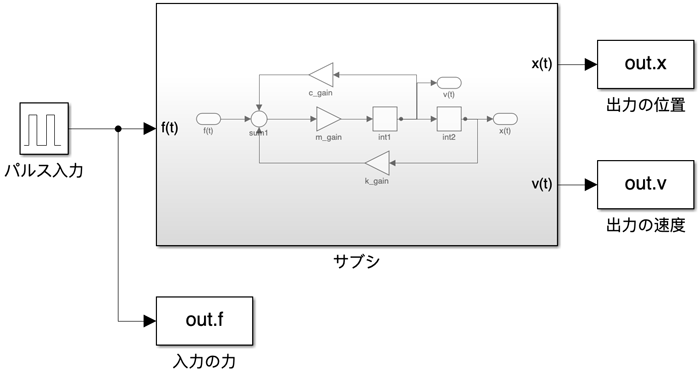
実行すると、以下のようなモデルが作成されます。

qsimo10.png

サブシステムを展開すると以下のようになります。これは前回の例で使用した伝達関数ブロックと同等の機能を持っていますが、速度$v(t)$も同時に出力している点が異なります。伝達関数ブロックをそのまま使用した場合、このように複数の出力を同時に取得することはできません。

qsimo11.png

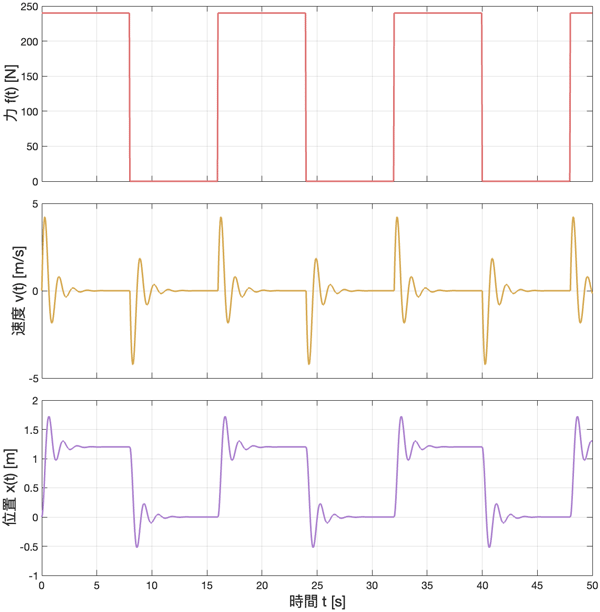
モデル実行の結果を用いて描画したグラフは以下の通りです。

qsimo12.png

これまでに説明したブロックに加え、今回のモデルで使用したブロックは以下の通りです。

終わりに

以上、MATLABスクリプトを使用してSimulinkモデルを操作する方法を紹介しました。

この方法はGUI操作よりも柔軟性が高く、様々な設定を自由に変更できます。また繰り返し実行やバッチ処理にも適しています。

ただし、GUI操作でブロック線図を確認しながら作成する方が直感的で分かりやすいこともあります。両方の方法を組み合わせて使用するのが良いでしょう。

参考

1
1
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?