本家ブログ(実践ケモインフォマティクス)もよろしくお願いします。
概要
-
回帰分析:目的変数と説明変数の関係をモデル化し、説明変数によって目的変数がどれだけ説明できるのかを定量的に分析すること。
(説明変数が一つなら単回帰分析、複数なら重回帰分析と呼ぶ) - Multiple Linear Regression(MLR)、Ordinary Least Squares(OLS)、Classical Linear Regression(CLS)などと呼ばれる
- 説明変数同士の相関が強い(多重共線性)がある場合は、回帰係数が不安定になるなど、正則化や次元削減といった対策が必要
単回帰分析
回帰分析の最も単純(説明変数が一つの場合)について考える。
$N$個のデータ($x_i$, $y_i$, $i=1,2,...,N$)がある時、これらのデータに対する近似直線
は実測値と予測値の差の二乗(二乗誤差|式2)が最も小さくなるような $w_0$, $w_1$ を求めるできる。
$$ y = w_0 + w_1 x_1 \qquad (1) $$
$$ \sum_{i=1}^{N} \{ y_i - (x_0+w_1x_1 ) \} ^2 \qquad (2)$$
重回帰分析
単回帰分析では1つだった説明変数が複数になった場合の各変数の重み(係数)を求める。
つまり、下式 $w_0$~$w_n$を求めることで、説明変数 $x$ が変化した時に目的変数がどれだけ変化するか(≒寄与の度合い)を求めることが、できたり、ある説明変数の組みが与えられたときの目的変数の値を予測することができる。
$$ y = w_0 + w_1 x_1 + \cdots + w_nx_n \qquad (3) $$
その他算出できる統計量など
- 偏回帰係数:各係数のこと。
-
標準偏回帰係数:説明変数及び目的変数を標準化したデータから算出される偏回帰係数のこと。各変数のスケールが揃っているため、各標準化偏回帰係数同士の大小を比較することができる。
(標準化:変数の平均値が0、分散が1になるように変数を変換すること) - 係数の標準誤差(SE|Std.Error):係数の推定値の標準誤差。小さいほど精度の高い推定といえる。
-
t 統計量:各偏回帰係数(定数項も含む)が0であるか検定するための統計量。
帰無仮説は「偏回帰係数=0」として、下式から求めたt値が自由度$(n-k-1)$の $t$分布に従うとして検定を行う。
($n$:サンプルサイズ、$k$:説明変数の数、$\hat{\beta_i}$:偏回帰係数、$se(\hat{\beta_i})$:変数 $i$ の係数の標準誤差)
$$ t_i = \frac{\hat{\beta_i} - 0}{se(\hat{\beta_i})}$$
- (t検定基づく) p 値:自由度$(n-k-1)$の $t$分布において、$t$ 値が上記で求めた値となる確率のこと。一般的にp値が5%または1%以下の場合に帰無仮説を棄却する。
-
偏回帰係数の信頼区間:自由度$(n-k-1)$の$t$分布を使い、下記式から偏回帰係数 $\hat{\beta}$ の $(100(1-\alpha)$%の信頼区間を求めることができる。
($n$:サンプルサイズ、$k$:説明変数の数、$t_{\frac{\alpha}{2}}(n-k-1)$:自由度が$(n-k-1)$の$t$分布における上側確率 $\frac{\alpha}{2}$ がとなる値 $t$ 値)
$$ \hat{\beta_i} - t_{\frac{\alpha}{2}}(n-k-1) \times se(\hat{\beta_i})\, \leq \, \hat{\beta_i} \, \leq \,\hat{\beta_i} + t_{\frac{\alpha}{2}}(n-k-1) \times se(\hat{\beta_i})$$
- 決定係数(R-squared):「目的変数のばらつきのうち、説明変数で説明できる割合」であり、回帰式の当てはまりの良さを表す。1が最も良い。
- 自由度修正済み決定係数(Adjusted R-squared):説明変数の数を考慮した上で当てはまりの良さを判断するのに用いる。
- F統計量(F-statistic):回帰式が意味があるかどうか(=「全ての係数がゼロである」という帰無仮説)を検定する統計量。
- (F検定に基づく) p 値:F統計量から算出できるp値。一般的にp値が5%または1%以下の場合に帰無仮説を棄却する。
コード
scikit-learnのワインのデータを使って重回帰分析を行ってみる。
アルコール濃度以外のデータを使って、アルコール濃度を回帰で求めてみる。
scikit-learn及び、StatsModelの2つのパターンを実施。
データの準備〜可視化まで
import pandas as pd
from sklearn import datasets
import seaborn as sns
import matplotlib.pyplot as plt
# load datasets
wine_data = datasets.load_wine()
df = pd.DataFrame(wine_data.data, columns=wine_data.feature_names)
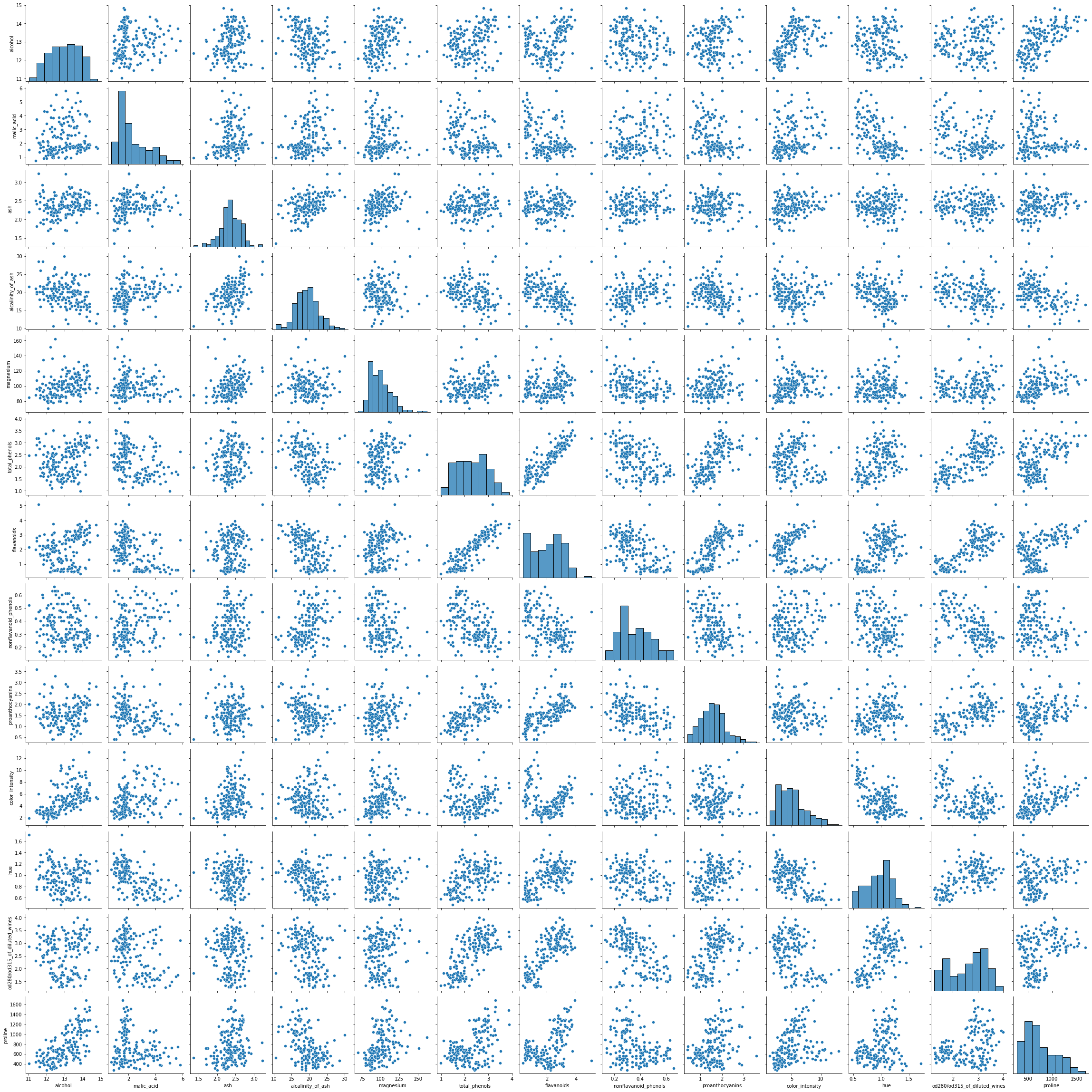
# 変数同士の関係性を見てみる。
graph = sns.pairplot(df)
graph.savefig('pairPlot.png')
plt.show()
scikit-learn を使った重回帰分析
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_absolute_error,mean_squared_error
import numpy as np
# 統計検定である"alcohol"を除いたデータセットと、アルコールだけのデータセットを作成
df_X = df.drop('alcohol', axis=1)
df_y = df['alcohol']
# 回帰
model = LinearRegression()
model.fit(df_X, df_y)
pred_y = model.predict(df_X)
print('決定係数(r2):{}'.format(round(r2_score(df_y, pred_y),3)))
print('平均誤差(MAE):{}'.format(round(mean_absolute_error(df_y, pred_y),3)))
print('RMSE:{}'.format(round(np.sqrt(mean_squared_error(df_y, pred_y)),3)))
"""output
決定係数(r2):0.594
平均誤差(MAE):0.408
RMSE:0.516
"""
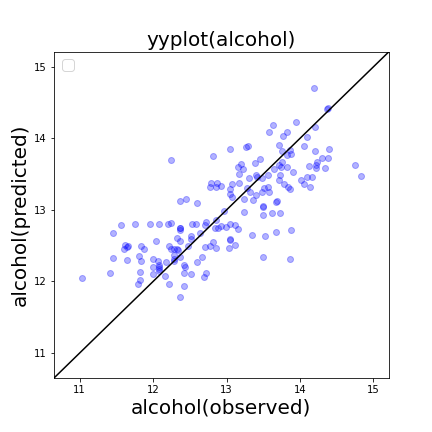
# 予測実測プロットの作成
plt.figure(figsize=(6,6))
plt.scatter(df_y, pred_y,color='blue',alpha=0.3)
y_max_ = max(df_y.max(), pred_y.max())
y_min_ = min(df_y.min(), pred_y.min())
y_max = y_max_ + (y_max_ - y_min_) * 0.1
y_min = y_min_ - (y_max_ - y_min_) * 0.1
plt.plot([y_min , y_max],[y_min, y_max], 'k-')
plt.ylim(y_min, y_max)
plt.xlim(y_min, y_max)
plt.xlabel('alcohol(observed)',fontsize=20)
plt.ylabel('alcohol(predicted)',fontsize=20)
plt.legend(loc='best',fontsize=15)
plt.title('yyplot(alcohol)',fontsize=20)
plt.savefig('yyplot.png')
plt.show()
print('回帰係数:',round(model.intercept_,3))
"""output
回帰係数: 11.072
"""
# 回帰係数を格納したpandasDataFrameの表示
df_coef = pd.DataFrame({'coefficient':model.coef_.flatten()}, index=df_X.columns)
# グラフの作成
x_pos = np.arange(len(df_coef))
fig = plt.figure(figsize=(6,6))
ax1 = fig.add_subplot(1, 1, 1)
ax1.barh(x_pos, df_coef['coefficient'], color='b')
ax1.set_title('coefficient of variables',fontsize=18)
ax1.set_yticks(x_pos)
ax1.set_yticks(np.arange(-1,len(df_coef.index))+0.5, minor=True)
ax1.set_yticklabels(df_coef.index, fontsize=14)
ax1.set_xticks(np.arange(-3,4,2)/10)
ax1.set_xticklabels(np.arange(-3,4,2)/10,fontsize=12)
ax1.grid(which='minor',axis='y',color='black',linestyle='-', linewidth=1)
ax1.grid(which='major',axis='x',linestyle='--', linewidth=1)
plt.savefig('coef_sklearn.png',bbox_inches='tight')
plt.show()
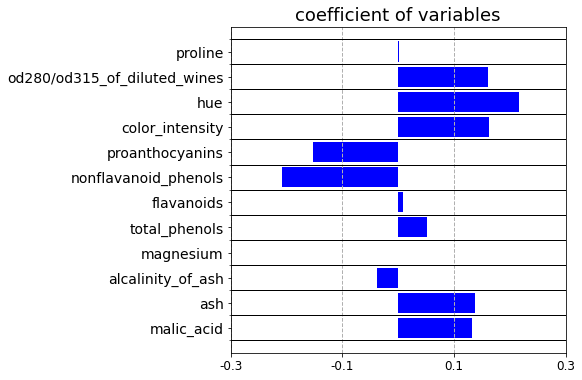
各回帰係数の可視化
StatsModelを使った重回帰分析
import statsmodels.api as sm
# 統計検定である"alcohol"を除いたデータセットと、アルコールだけのデータセットを作成
df_X = df.drop('alcohol', axis=1)
df_y = df['alcohol']
df_X = sm.add_constant(df_X)
model = sm.OLS(df_y, df_X)
result = model.fit()
print(result.summary())
"""output
OLS Regression Results
==============================================================================
Dep. Variable: alcohol R-squared: 0.594
Model: OLS Adj. R-squared: 0.564
Method: Least Squares F-statistic: 20.08
Date: Thu, 01 Jul 2021 Prob (F-statistic): 1.61e-26
Time: 22:23:20 Log-Likelihood: -134.83
No. Observations: 178 AIC: 295.7
Df Residuals: 165 BIC: 337.0
Df Model: 12
Covariance Type: nonrobust
================================================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------------------------
const 11.0718 0.596 18.567 0.000 9.894 12.249
malic_acid 0.1316 0.045 2.907 0.004 0.042 0.221
ash 0.1379 0.217 0.636 0.526 -0.290 0.566
alcalinity_of_ash -0.0378 0.018 -2.122 0.035 -0.073 -0.003
magnesium 4.179e-06 0.003 0.001 0.999 -0.007 0.007
total_phenols 0.0521 0.134 0.389 0.698 -0.212 0.317
flavanoids 0.0091 0.107 0.085 0.932 -0.202 0.220
nonflavanoid_phenols -0.2078 0.434 -0.479 0.632 -1.064 0.648
proanthocyanins -0.1525 0.098 -1.552 0.122 -0.346 0.041
color_intensity 0.1630 0.027 5.941 0.000 0.109 0.217
hue 0.2169 0.281 0.772 0.441 -0.338 0.772
od280/od315_of_diluted_wines 0.1608 0.110 1.466 0.145 -0.056 0.377
proline 0.0010 0.000 5.081 0.000 0.001 0.001
==============================================================================
Omnibus: 0.348 Durbin-Watson: 1.998
Prob(Omnibus): 0.840 Jarque-Bera (JB): 0.121
Skew: 0.025 Prob(JB): 0.941
Kurtosis: 3.118 Cond. No. 1.27e+04
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.27e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
"""
予測精度や各統計量などが表示できる。
各変数に着目してみると、p値が十分小さい変数は係数の95%信頼区間が0を通らないため、有意な変数であることが読み取れる。(例|変数malic_acid のp値は0.004で、95%信頼区間は0.042〜0.221)
一方で、p値が大きい変数は係数の95%信頼区間が0を通るため、有意でない変数(係数が0である可能性がある)であることが読み取れる(例|変数 ash のp値は0.526で、95%信頼区間は−0.290〜0.566)
その他の統計量の説明はこちらのHP参照。
詳細説明
重回帰分析・最小二乗法の解説
単回帰分析では1つだった説明変数が複数になった場合の各変数の重み(係数)を求める。
つまり式3の $w_0$~$w_n$を求める。
$$ y = w_0 + w_1 x_1 + \cdots + w_nx_n \qquad (3) $$
式3を行列の形にすると、式4となる。
(全ての説明変数の行列を$\boldsymbol{X}$、係数の行列を$\boldsymbol{w}$とおき、$x_0=1$とする)
y =
\begin{bmatrix}
x_0&x_1& x_2 & \cdots &x_n
\end{bmatrix}
\begin{bmatrix}
w_0 \\
w_1 \\
w_2 \\
\vdots \\
w_n \\
\end{bmatrix}
= \boldsymbol{X}\boldsymbol{w}
\qquad (4)
実測値 $\hat{y}$ と計算値の誤差の二乗和($E$)を計算し、それが最小値となるような係数$\boldsymbol{w}$ を求める。
この一連の流れを最小二乗法という。
$$ \begin{align} E = \sum_{i=1}^{n}(y-\hat{y})^2 &=(\boldsymbol{y}-\hat{\boldsymbol{y}})^{T}(\boldsymbol{y}-\hat{\boldsymbol{y}}) \\ &= (\boldsymbol{y}-\boldsymbol{Xw})^{T}(\boldsymbol{y}-\boldsymbol{Xw}) \\ &= (\boldsymbol{y}^{T}-(\boldsymbol{Xw})^{T})(\boldsymbol{y}-\boldsymbol{Xw}) \\ &= (\boldsymbol{y}^{T}-\boldsymbol{w}^{T}\boldsymbol{X}^{T})(\boldsymbol{y}-\boldsymbol{Xw}) \\ &= \boldsymbol{y}^{T}\boldsymbol{y}-\boldsymbol{y}^{T}\boldsymbol{X}\boldsymbol{w}-\boldsymbol{w}^{T}\boldsymbol{X}^{T}\boldsymbol{y}-\boldsymbol{w}^{T}\boldsymbol{X}^{T}\boldsymbol{X}\boldsymbol{w} \\ &= \boldsymbol{y}^{T}\boldsymbol{y}-2\boldsymbol{y}^{T}\boldsymbol{X}\boldsymbol{w}-\boldsymbol{w}^{T}\boldsymbol{X}^{T}\boldsymbol{X}\boldsymbol{w} \end{align} $$
$E$ は $\boldsymbol{w}$ の関数であり、二乗誤差が最も小さくなる点では、$E$ の傾きが0になるはずである。
二次形式とベクトルの微分の公式(以下2つ)を利用して二乗誤差$E$を$\boldsymbol{w}$について微分すると
$$
\frac{\partial\boldsymbol{w}^T\boldsymbol{x}}{\partial\boldsymbol{w}} = \boldsymbol{x} \ \frac{\partial\boldsymbol{w}^TX\boldsymbol{w}}{\partial\boldsymbol{w}} = (X + X^T)\boldsymbol{w}
$$
$$ \begin{align} \frac{\partial E}{\partial\boldsymbol{w}} &= -2\boldsymbol{X}^T\boldsymbol{y} + (\boldsymbol{X}\boldsymbol{X}^T + \boldsymbol{X}^T\boldsymbol{X})\boldsymbol{w} \\ &= -2\boldsymbol{X}^T\boldsymbol{y} + 2\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{w} \end{align}
$$
$$ \frac{\partial E}{\partial\boldsymbol{w}} = 0$$
となるためには、$$ \boldsymbol{X}^T\\boldsymbol{y} = \boldsymbol{X}^T\boldsymbol{X}\\boldsymbol{w} $$
よって、重み(係数) $\boldsymbol{w}$ は
$$ \boldsymbol{w} = (\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\\boldsymbol{y} $$
となる。上記式を解けば重み(係数) $\boldsymbol{w}$ がもとまるが、逆に言えば、$\boldsymbol{X}^T\boldsymbol{X}$ が正則でないと$\boldsymbol{w}$ は算出できない。
例えば、変数 $x$ 同士に強い相関がある場合、つまりどちらか一方のデータ列で別のデータ列が説明できる場合に正則にならない。
この状態を多重共線性、通称(マルチコ:multicollinearity)があるという。