はじめに
以前、「機械学習の分類」で取り上げたアルゴリズムについて、その理論とpythonでの実装、scikit-learnを使った分析についてステップバイステップで学習していく。個人の学習用として書いてるので間違いなんかは大目に見て欲しいと思います。
今回は単回帰分析を発展させ、「重回帰分析」をやってみたいと思います。参考にしたのは次のページです。
基本
単回帰分析では、平面上の$N$個の$(x, y)$に対する近似直線$$ y = Ax + B $$を引くための$A$と$B$を求めました。具体的には、直線と$i$番目の点の差の二乗の和$$\sum_{i=1}^{N} (y_i-(Ax+B))^2$$が最も小さくなるような$A$と$B$を求めました。
重回帰は、単回帰で1つだった変数(説明変数)を増やした場合の係数を求めるものです。
つまり、直線の式を$$ y=w_0x_0+w_1x_1+\cdots+w_nx_n$$とおいた場合($x_0=1$とする)の$ (w_0, w_1, \cdots, w_n)$を求めればよいことになる。
重回帰の解き方
ここからはほぼ参考にした記事のパクリに近くなってしまうのだが、できるだけわかりやすく書くよう努力します。
直線の式を行列の形にすると、
y = \begin{bmatrix} w_0 \\ w_1 \\ w_2 \\ \vdots \\ w_n \end{bmatrix} \begin{bmatrix} x_0, x_1, x_2, \cdots, x_n\end{bmatrix}
となる($x_0=1$)。
実測値$\hat{y}$との差の二乗和は$$ \sum_{i=1}^{n}(y-\hat{y})^2$$となるので、これを変形していく。なお、$(w_0, w_1, \cdots, w_n)$を$\boldsymbol{w}$、全ての説明変数を行列$\boldsymbol{X}$とする。
\sum_{i=1}^{n}(y-\hat{y})^2 \\
= (\boldsymbol{y}-\hat{\boldsymbol{y}})^{T}(\boldsymbol{y}-\hat{\boldsymbol{y}}) \\
= (\boldsymbol{y}-\boldsymbol{Xw})^{T}(\boldsymbol{y}-\boldsymbol{Xw}) \\
= (\boldsymbol{y}^{T}-(\boldsymbol{Xw})^{T})(\boldsymbol{y}-\boldsymbol{Xw}) \\
= (\boldsymbol{y}^{T}-\boldsymbol{w}^{T}\boldsymbol{X}^{T})(\boldsymbol{y}-\boldsymbol{Xw}) \\
= \boldsymbol{y}^{T}\boldsymbol{y}-\boldsymbol{y}^{T}\boldsymbol{X}\boldsymbol{w}-\boldsymbol{w}^{T}\boldsymbol{X}^{T}\boldsymbol{y}-\boldsymbol{w}^{T}\boldsymbol{X}^{T}\boldsymbol{X}\boldsymbol{w} \\
= \boldsymbol{y}^{T}\boldsymbol{y}-2\boldsymbol{y}^{T}\boldsymbol{X}\boldsymbol{w}-\boldsymbol{w}^{T}\boldsymbol{X}^{T}\boldsymbol{X}\boldsymbol{w}
$\boldsymbol{w}$に無関係なものは定数なので、それぞれ$\boldsymbol{X}^{T}\boldsymbol{X}=A$、$-2\boldsymbol{y}^{T}\boldsymbol{X}=B$、$\boldsymbol{y}^{T}\boldsymbol{y}=C$とおくと、最小二乗和$L$は、$$ L = C-B\boldsymbol{w}-\boldsymbol{w}^{T}A\boldsymbol{w}$$となる。
$L$は$\boldsymbol{w}$の二次関数であるため、$L$が最小となる$\boldsymbol{w}$は、$L$を$\boldsymbol{w}$で偏微分した式が0になる$\boldsymbol{w}$を求めればよいことになる。
\begin{split}\begin{aligned}
\frac{\partial}{\partial {\boldsymbol{w}}} L
&= \frac{\partial}{\boldsymbol{w}} (C + B\boldsymbol{w} + \boldsymbol{w}^T{A}\boldsymbol{w}) \\
&=\frac{\partial}{\partial {\boldsymbol{w}}} (C) + \frac{\partial}{\partial {\boldsymbol{w}}} ({B}{\boldsymbol{w}}) + \frac{\partial}{\partial {\boldsymbol{w}}} ({\boldsymbol{w}}^{T}{A}{\boldsymbol{w}}) \\
&={B} + {w}^{T}({A} + {A}^{T})
\end{aligned}\end{split}
これを0にしたいので、
\boldsymbol{w}^T(A+A^T)=-B \\
\boldsymbol{w}^T(\boldsymbol{X}^{T}\boldsymbol{X}+(\boldsymbol{X}^{T}\boldsymbol{X})^T)=2\boldsymbol{y}^{T}\boldsymbol{X} \\
\boldsymbol{w}^T\boldsymbol{X}^{T}\boldsymbol{X}=\boldsymbol{y}^T\boldsymbol{X} \\
\boldsymbol{X}^{T}\boldsymbol{X}\boldsymbol{w} = \boldsymbol{X}^T\boldsymbol{y} \\
この形は連立一次方程式の形で、$\boldsymbol{X}^{T}\boldsymbol{X}$が正則でないと連立方程式が解けません。どこかの$x$に強い相関がある場合、つまりどちらか一方のデータ列で別のデータ列が説明できる場合に正則になりません。この状態を多重共線性、通称(マルチコ:multicollinearity)があると言います。
正則であると仮定すると、
(\boldsymbol{X}^{T}\boldsymbol{X})^{-1}\boldsymbol{X}^{T}\boldsymbol{X}\boldsymbol{w}=(\boldsymbol{X}^{T}\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y} \\
\boldsymbol{w}=(\boldsymbol{X}^{T}\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}
これで$\boldsymbol{w}$が求まりました。
ptyhonで愚直に実装してみる
データはscikit-learnの糖尿病データ(diabetes)を使います。ターゲット(1年後の進行状況)とBMI、S5(ltg:ラモトリオギン)のデータがどう関連しているか調べてみましょう。
まずはデータを眺める
まずはデータをプロットしてみる。説明変数が2つとターゲットなので3次元データになる。3次元をこえるとグラフはかけないですね。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns
%matplotlib inline
diabetes = datasets.load_diabetes()
df = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
fig=plt.figure()
ax=Axes3D(fig)
x1 = df['bmi']
x2 = df['s5']
y = diabetes.target
ax.scatter3D(x1, x2, y)
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_zlabel("y")
plt.show()
結果は次のグラフで、なんとなく斜面のような感じになっています。
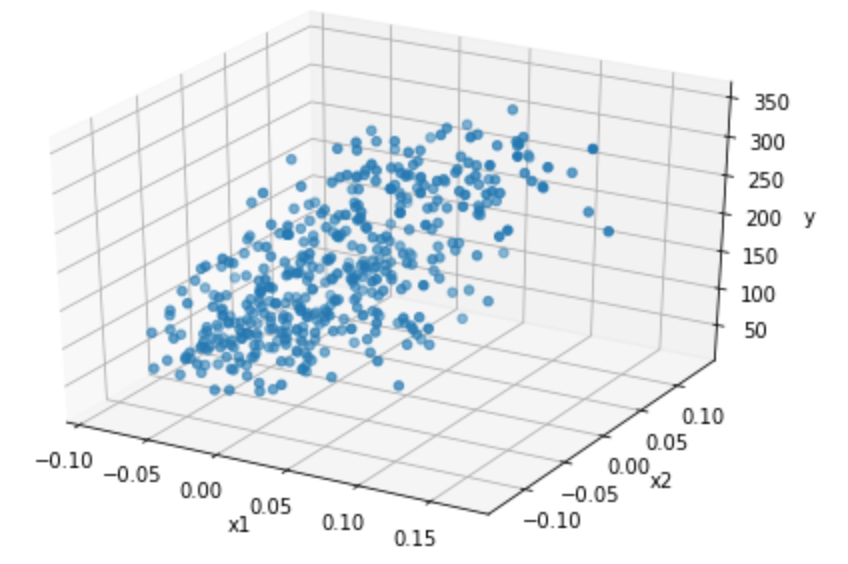
計算してみる
$ \boldsymbol{w} $を求める式は次のような式でした。正規方程式と言うらしいです。
$$ \boldsymbol{w}=(\boldsymbol{X}^{T}\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y} $$これをそのままコードにしてみます。
X = pd.concat([pd.Series(np.ones(len(df['bmi']))), df.loc[:,['bmi','s5']]], axis=1, ignore_index=True).values
y = diabetes.target
w = np.linalg.inv(X.T @ X) @ X.T @ y
結果:[152.13348416 675.06977443 614.95050478]
pythonの行列計算は直感的でいいですね。ちなみに、説明変数が1つの場合は単回帰と同じ結果になります。説明変数n個で一般化したから当然ですね。
X = pd.concat([pd.Series(np.ones(len(df['bmi']))), df.loc[:,['bmi']]], axis=1, ignore_index=True).values
y = diabetes.target
w = np.linalg.inv(X.T @ X) @ X.T @ y
print(w)
[152.13348416 949.43526038]
説明変数が2つのときの計算値をもとに、グラフを描いてみます。
fig=plt.figure()
ax=Axes3D(fig)
mesh_x1 = np.arange(x1.min(), x1.max(), (x1.max()-x1.min())/20)
mesh_x2 = np.arange(x2.min(), x2.max(), (x2.max()-x2.min())/20)
mesh_x1, mesh_x2 = np.meshgrid(mesh_x1, mesh_x2)
x1 = df['bmi'].values
x2 = df['s5'].values
y = diabetes.target
ax.scatter3D(x1, x2, y)
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_zlabel("y")
mesh_y = w[1] * mesh_x1 + w[2] * mesh_x2 + w[0]
ax.plot_wireframe(mesh_x1, mesh_x2, mesh_y, color='red')
plt.show()
結果は下記の図のようになりました。ちゃんとできてるようなできてないようなw
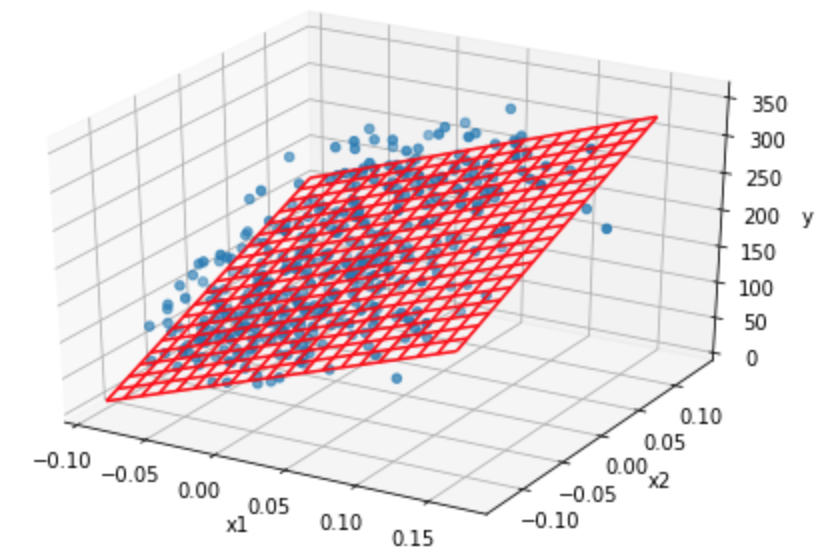
評価
平面の一致度を決定係数で評価してみる。
決定係数$R^2$は、「全変動」と「回帰変動」を求める必要がある。
- 全変動:実測値と全体の平均値の差
- 回帰変動:予測値と全体の平均の差
決定係数は、説明変数が目的変数をどれくらい説明しているか、つまり「回帰変動が全変動に対してどれだけ多いか」を求める。全変動と回帰変動の二乗和(分散)を用い、
R^2=\frac{\sum_{i=0}^{N}(\hat{y}_i-\bar{y})^2}{\sum_{i=0}^{N}(y_i-\bar{y})^2}
全変動は回帰変動と全差変動(予測値と実測値)の和なので、
R^2=1-\frac{\sum_{i=0}^{N}(y_i-\hat{y}_i)^2}{\sum_{i=0}^{N}(y_i-\bar{y})^2}
これをpythonで書いて、先ほどの決定係数を算出する。
u = ((y-(X @ w))**2).sum()
v = ((y-y.mean())**2).sum()
R2 = 1-u/v
print(R2)
0.4594852440167805
という結果になりました。
正規化、標準化
さて、今回の例では「BMI」と「ltg」の値を使いましたが、もっと変数が増えたりすると例えば$10^5$オーダの数字と$10^{-5}$オーダのデータが混在する可能性もあります。こうなってしまうと計算がうまくいかないことがおきます。元のデータを保ったままデータを揃えることを正規化(normalization)といいます。
Min-Maxスケーリング
Min-Maxスケーリングは最小値が-1、最大値が1となるように変換します。つまり、$$ x_{i_{new}}=\frac{x_i-x_{min}}{x_{max}-x_{min}} $$を計算します。
標準化(standardization)
標準化は、平均が0、分散が1となるように変換します。つまり、$$ x_{i_{new}}=\frac{x_i-\bar{x}}{\sigma} $$を計算します。
以下のページに詳しく書いています。
pythonで標準化してみる
pythonで計算してみようとしたんですが、どうもscikit-learnのdiabetesデータはすでに正規化されてるみたいで意味がありませんでしたw
scikit-learnで計算してみる
重回帰はscikit-learnのLinearRegressionを使い、学習データでfitさせるだけです。
from sklearn import linear_model
clf = linear_model.LinearRegression()
clf.fit(df[['bmi', 's5']], diabetes.target)
print("coef: ", clf.coef_)
print("intercept: ", clf.intercept_)
print("score: ", clf.score(df[['bmi', 's5']], diabetes.target))
coef: [675.06977443 614.95050478]
intercept: 152.1334841628967
score: 0.45948524401678054
これだけです。結果はscikit-learnを使わない結果と一緒になりましたね。
まとめ
単回帰から重回帰に発展させました。正規方程式
$$ \boldsymbol{w}=(\boldsymbol{X}^{T}\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y} $$に一般化させることで、複数の説明変数に拡張することができました。複数の説明変数はスケールを揃える必要があるので、標準化という手法で粒度を揃えて計算する必要があります。
これで線形近似は理解できましたね。