StatsModelsによる重回帰解析

StatsModelsを使って、Boston Housingデータセットを重回帰解析します。
scikit-learnを用いた重回帰解析の例はよく見られますが、ここでは、StatsModelsを用いて重回帰解析を行います。
StatsModelsを使うと、解析の結果得られた重回帰式の精度を表す各指標を表示することが可能です。

$$y = w_0x_0 + w_1x_1 + ... + w_mx_m = \sum_{i=0}^{m}w_ix_i=w^Tx$$

データの準備

Housingデータセットの特徴量

• CRIM：犯罪発生率
• ZN：25,000兵法フィールド以上の住宅区画の割合
• INDUS：非小売業の土地面積の割合（人口単位）
• CHRS：チャールズ川沿いかどうか
• NOX：窒素酸化物の濃度（pphm単位）
• AGE：1940年よりも前に建てられた家屋の割合
• DIS：ボストンの主な5つの雇用圏までの重み付きの距離
• RAD：幹線道路へのアクセス指数
• TAX：10,000ドル当たりの所得税率
• PTRATIO：教師当たりの生徒数（人工単位）
• B：$1000(Bk-0.63)^2$として計算、$Bk$はアフリカ系アメリカ人居住者の割合（人口単位）
• LSTAT：低所得者の割合
• MDEV：住宅価格の中央値（単位1,000ドル）

データのダウンロード

import pandas as pd

df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data',
                 header=None, sep='\s+')
df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
              'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
df.head()

CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT	MEDV
0	0.00632	18.0	2.31	0	0.538	6.575	65.2	4.0900	1	296.0	15.3	396.90	4.98	24.0
1	0.02731	0.0	7.07	0	0.469	6.421	78.9	4.9671	2	242.0	17.8	396.90	9.14	21.6
2	0.02729	0.0	7.07	0	0.469	7.185	61.1	4.9671	2	242.0	17.8	392.83	4.03	34.7
3	0.03237	0.0	2.18	0	0.458	6.998	45.8	6.0622	3	222.0	18.7	394.63	2.94	33.4
4	0.06905	0.0	2.18	0	0.458	7.147	54.2	6.0622	3	222.0	18.7	396.90	5.33	36.2

データセットの可視化

散布図行列

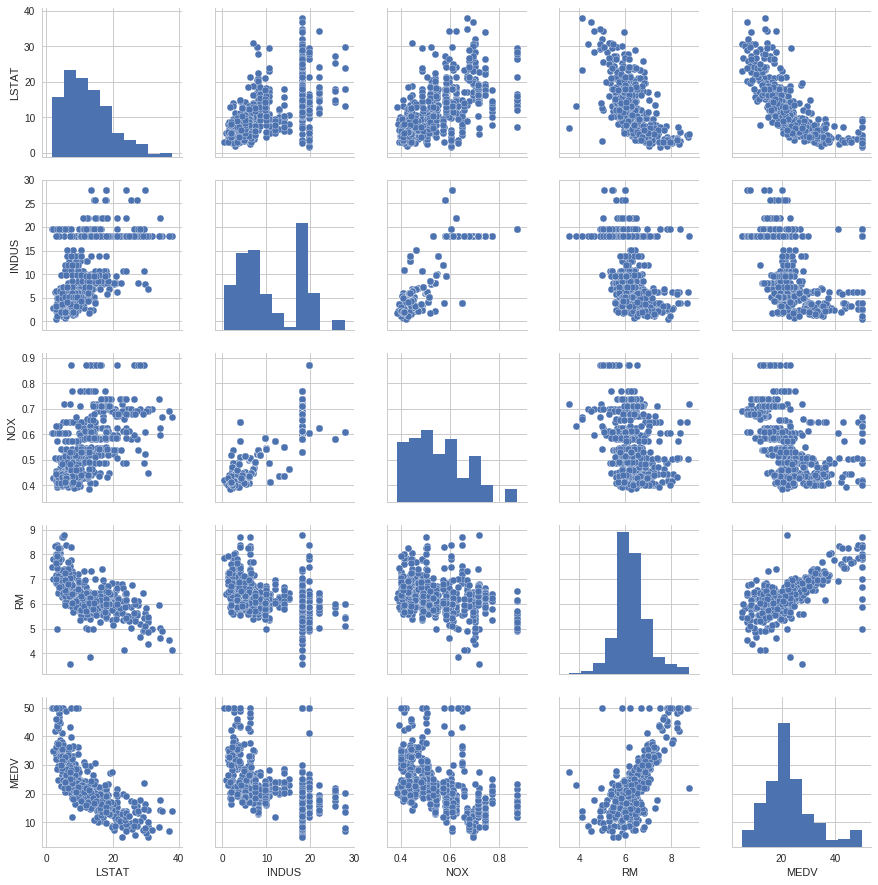
全変数を対象とすると、図が小さくなってしまうので、ここでは、LSTAT、INOUS、NOX、RMとMEDVを対象に散布図行列を作っています。

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns

sns.set(style='whitegrid', context='notebook')
cols = ['LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']
sns.pairplot(df[cols], size=2.5)
plt.show()

相関行列のヒートマップ

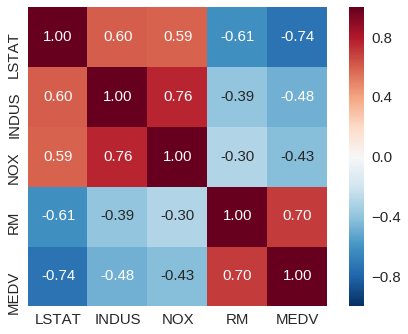
import numpy as np

cm = np.corrcoef(df[cols].values.T)
sns.set(font_scale=1.5)
hm = sns.heatmap(cm,
                 cbar=True,
                 annot=True,
                 square=True,
                 fmt='.2f',
                 annot_kws={'size': 15},
                 yticklabels=cols,
                 xticklabels=cols)
plt.show()

相関係数が1に近づくほど、正の相関が高く、-1に近づくほど、負の相関が高くなるとされています。0は、無相関を表します。

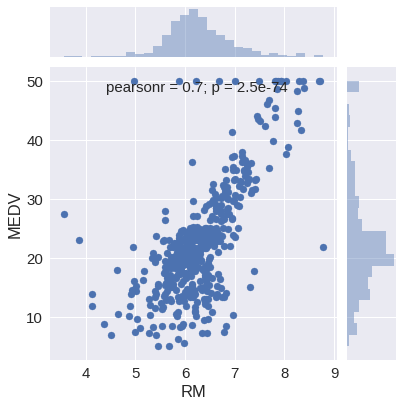
部屋数と価格の散布図とヒストグラム

sns.jointplot('RM', 'MEDV', data=df)
plt.show()

重回帰解析

import statsmodels.api as sm

X = df.drop('MEDV', 1)
X = sm.add_constant(X)
Y = df['MEDV']
model = sm.OLS(Y, X)
result = model.fit()
result.summary()

OLS Regression Results
Dep. Variable:	MEDV	R-squared:	0.741
Model:	OLS	Adj. R-squared:	0.734
Method:	Least Squares	F-statistic:	108.1
Date:	Mon, 13 Aug 2018	Prob (F-statistic):	6.72e-135
Time:	08:41:48	Log-Likelihood:	-1498.8
No. Observations:	506	AIC:	3026.
Df Residuals:	492	BIC:	3085.
Df Model:	13
Covariance Type:	nonrobust

	coef	std err	t	P>t	[0.025	0.975]
const	36.4595	5.103	7.144	0.000	26.432	46.487
CRIM	-0.1080	0.033	-3.287	0.001	-0.173	-0.043
ZN	0.0464	0.014	3.382	0.001	0.019	0.073
INDUS	0.0206	0.061	0.334	0.738	-0.100	0.141
CHAS	2.6867	0.862	3.118	0.002	0.994	4.380
NOX	-17.7666	3.820	-4.651	0.000	-25.272	-10.262
RM	3.8099	0.418	9.116	0.000	2.989	4.631
AGE	0.0007	0.013	0.052	0.958	-0.025	0.027
DIS	-1.4756	0.199	-7.398	0.000	-1.867	-1.084
RAD	0.3060	0.066	4.613	0.000	0.176	0.436
TAX	-0.0123	0.004	-3.280	0.001	-0.020	-0.005
PTRATIO	-0.9527	0.131	-7.283	0.000	-1.210	-0.696
B	0.0093	0.003	3.467	0.001	0.004	0.015
LSTAT	-0.5248	0.051	-10.347	0.000	-0.624	-0.425

Omnibus:	178.041	Durbin-Watson:	1.078
Prob(Omnibus):	0.000	Jarque-Bera (JB):	783.126
Skew:	1.521	Prob(JB):	8.84e-171
Kurtosis:	8.281	Cond. No.	1.51e+04

scikit-learnだと、解析結果のサマリーが取得できないようです。

• 決定係数（R-squared）：0.741
• 自由度調整済み決定係数（Adj. R-squared）：0.734
• 有意F（Prob (F-statistic)）：6.72e-135
• 各係数のP値：-0.1080, 0.0464, 0.0206, -17.7666, ...

StatsModelsの場合、以下のように個々の指標を取得することもできます。

print('重決定R2:{:.4f}, 補正R2:{:.4f}, 有意F:{:.4f}, 切片:{:.4f}, 係数1:{:.4f}, P値1:{:.4f}, 係数2:{:.4f}, P値2:{:.4f}, ...'.format(
    result.rsquared, result.rsquared_adj, result.f_pvalue,
    result.params[0], result.params[1], result.pvalues[1], result.params[2], result.pvalues[2]))

重決定R2:0.7406, 補正R2:0.7338, 有意F:0.0000, 切片:36.4595, 係数1:-0.1080, P値1:0.0011, 係数2:0.0464, P値2:0.0008, ...

Excelでの検証

!pip install -U -q PyDrive

from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from google.colab import auth
from oauth2client.client import GoogleCredentials

auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)

df.to_excel('housing.xlsx')

upload_file_2 = drive.CreateFile()
upload_file_2.SetContentFile('housing.xlsx')
upload_file_2.Upload()

Excelでの解析結果

StatsModelsで得られた数値がExcelで得られた数値と一致しています。

回帰統計
重相関 R	0.860605987
重決定 R2	0.740642664
補正 R2	0.733789726
標準誤差	4.745298182
観測数	506

分散分析表
	自由度	変動	分散	観測された分散比	有意 F
回帰	13	31637.51084	2433.65468	108.0766662	6.72E-135
残差	492	11078.78458	22.51785483
合計	505	42716.29542

	係数	標準誤差	t	P-値	下限 95%	上限 95%	下限 95.0%	上限 95.0%
切片	36.45948839	5.103458811	7.144074193	3.28E-12	26.43222601	46.48675076	26.43222601	46.48675076
CRIM	-0.108011358	0.032864994	-3.286516871	0.00108681	-0.172584412	-0.043438304	-0.172584412	-0.043438304
ZN	0.046420458	0.013727462	3.381576282	0.00077811	0.019448778	0.073392139	0.019448778	0.073392139
INDUS	0.020558626	0.061495689	0.334310042	0.738288071	-0.100267941	0.141385193	-0.100267941	0.141385193
CHAS	2.686733819	0.861579756	3.118380858	0.00192503	0.993904193	4.379563446	0.993904193	4.379563446
NOX	-17.76661123	3.819743707	-4.651257411	4.25E-06	-25.27163356	-10.26158889	-25.27163356	-10.26158889
RM	3.809865207	0.417925254	9.1161402	1.98E-18	2.988726773	4.63100364	2.988726773	4.63100364
AGE	0.000692225	0.013209782	0.052402427	0.958229309	-0.02526232	0.026646769	-0.02526232	0.026646769
DIS	-1.475566846	0.199454735	-7.398003603	6.01E-13	-1.867454981	-1.08367871	-1.867454981	-1.08367871
RAD	0.306049479	0.06634644	4.612899768	5.07E-06	0.175692169	0.436406789	0.175692169	0.436406789
TAX	-0.012334594	0.003760536	-3.28000914	0.001111637	-0.019723286	-0.004945902	-0.019723286	-0.004945902
PTRATIO	-0.952747232	0.130826756	-7.282510564	1.31E-12	-1.209795296	-0.695699168	-1.209795296	-0.695699168
B	0.009311683	0.002685965	3.466792558	0.000572859	0.004034306	0.01458906	0.004034306	0.01458906
LSTAT	-0.524758378	0.050715278	-10.3471458	7.78E-23	-0.624403622	-0.425113133	-0.624403622	-0.425113133

参考

• Python 機械学習プログラミング 達人データサイエンティストによる理論と実践
• Tables Generator