本記事はWACUL Advent Calendar 2017の12/25の記事になります。
こんにちは、株式会社WACULで、データ分析の仕事をしている@onhrsです。
現在、機械学習エンジニアをしておりますが、数学や物理などが好きなので（できるとは言ってません）、今でも重力波を解析したり、量子アニーリングのイジングモデルを計算したりしております。
今回は、徐々に浸透してきた量子コンピュータについて、最近の動向を含め個人的に勉強しまとめてみました。とりあえず量子コンピュータは何か、量子アルゴリズムとは何かっていうのがわかってもらえたらと思います。
はじめに
今回参考にした書籍です
全体な流れは量子コンピューター
量子コンピュータとは何か (ハヤカワ文庫NF―数理を愉しむシリーズ)
量子アルゴリズムについては
量子コンピュータ―超並列計算のからくり (ブルーバックス)
どちらも10年以上前の書籍で、少々古いものでしたが、直感で理解するのにはちょうどいい書籍であると思います。ブルーバックスの方は数式も出てきて少し難しいものだと思うので、数式を使わず理解したい方はハヤカワ文庫の方から読むことをお勧めします。
##量子コンピューターとは何か
量子コンピューティングは、重ね合わせと絡み合い（エンタングルメント）などに代表される量子力学的現象を用いたコンピューターのことです。ここでいうエンタングルメント（量子エンタングルメント）とは、粒子のペアまたはグループが生成されたり相互作用し合って、各粒子の量子状態を他の粒子とは独立して記述できない物理的現象のことです。
具体的に説明していきます。
#扱える情報量が飛躍的に増加する
従来のコンピューターの演算は電流が流れる時に1に対応させて、電流が流れない時に0の2つの状態のみで、それらを組み合わせることで複雑な計算をしておりましたが、量子コンピュータの演算は0と1の間の状態の状態を扱えると言われております。正しい解釈ではないかもしれませんが、矢印の上向きを1、矢印の下向きを0に対応させた場合、その間の向きは無数存在します。量子コンピュータとは、量子の重ね合わせ状態というものを作ることで、この無数の状態を作り出し、演算に活かすコンピューターのことをいいます。
#数式を使わない量子力学入門
##2重スリット実験（物質は粒子と波の性質を持っている）
ダムや川に2箇所穴が空いていた場合をイメージして見てください。
穴を抜けた段階で、新たな波が生成され、各スリットから発せられた波は互いに干渉し、大きい波同士がぶつかった時はさらに大きくなることで図のようにすることがわかります。
https://web2.ph.utexas.edu/~coker2/index.files/diff.htm
粒子の世界でも原子サイズまで小さくする時、上記と同様の現象が起こります。
上のように電子銃からいくつかの電子を発射する場合を想定します。
このような状態でも川の流れの時と同様に干渉した結果スクリーンには飛び飛びの粒子が出てくることが実験により証明されたのです。
http://gscim.com/phy/Quantum_Mechanics/double_slit_experiment.html
なぜこのようなことが起きるのでしょう。この現象をより深く学ぶため、物質の最小単位の電子1個（これ以上分割できない物質）をぶつけた場合を考えましょう。
なんと1つずつ発射したにもかかわらず、先ほどと同じような干渉パターンができたのです。
以上のことから、電子1つでも波として干渉する可能性が考えられます。
##波束の集束（観測時に物質の状態はきまる）
今度は、粒子がどちらを通ったかわかるようにスリットのところに物質がいくつ通るかわかるように観測機を設置します。
このように設置した結果、左右ともに同じ数の粒子を観測することができましたが、驚くことに、この時に結果の干渉縞は観測されないで粒子としての性質が現れます。
https://phys-and-program.com/entry/doubleslitexperiment
まだ核心には迫っておりませんが、以上の不思議な現象を用いて、演算するコンピューターが量子コンピューターの正体なのです。
この不思議な現象が一般の人にとって、量子力学をわからなくする原因であり、量子コンピュータはこの現象を用いて高速演算を可能にしているのです。
2重スリットについて、より詳しく知りたい方は、以下が分かり易かったです。
2重スリットの実験の解説動画
人知を超えた量子力学の世界。2重スリット実験がヤバイ・・・ｗｗｗ
二重スリット実験・観測問題を宇宙一わかりやすく物理学科が解説する
#量子エンタングルについて
観測することによって状態が変わるということは、厳密な証明は今だに解明されていないようですが、現代の量子論では様々な理論や、それを証明する実験結果から、現在では当たり前のものとして考えられています。
2重スリットの実験において、一つしか電子を照射していないにも関わらず、その一粒が上にも下にも通る事が可能で、それは観測するまで決定されませんでした。つまりは電子が上にも下にも通る確率があり、それは観測される瞬間に初めて決定され、観測されなければ、それまで状態が決して決まらないというのです。ややこしいですが、このことが、量子の絡み合い、エンタングルメントの正体なのです。
この具体例としては、シュレディンガーの猫の話がとても有名です。シュレディンガーの猫とは「ランダムの確率で毒ガスの出る装置とともに猫を箱の中に閉じ込めたとき、次に箱を開けた時まで、猫が死んだ可能性と生きている可能性は重なり合っている」とし、量子力学の奇妙さを指摘したものです。（シュレディンガーの猫 (しゅれーでぃんがーのねこ)とは【ピクシブ百科事典】より）
箱を開く前にも、箱の中で猫が死んでいるかどうか決定しているというふうに考えるのが普通ですが、2重スリットの実験同様に、"箱を開ける"という観測が行われない限り、あくまで猫は死んでいる状態と生きている状態が重なり合っているのです。
このことをネタとして面白く説明したものに、とある大学生のレポート期日に関してのコメントが有名です。
このようにして、どんな単純な状態（上を通ったor下を通った、生きているor死んでいるみたいな2つの状態）について、量子状態では、粒子のペアのグループが互いに相互作用し合います。繰り返しになりますが、これが量子エンタングルなのです。
#量子アルゴリズムについて
この重ね合わせの状態を用いてコンピュータの演算に用いるのが量子コンピューターなのですが、ここで量子コンピュータ実現のために、代表的なアルゴリズムであるショアのアルゴリズム、グローバーのアルゴリズムについて解説します。
##ショアのアルゴリズム
ショアのアルゴリズムは、素因数分解問題を高速に（多項式時間で）解くことができるアルゴリズムのことであります。（wikipediaより）
素因数分解は大きい数字になれば果てしなく難しいらしいです。（150～300桁の素数を用いた場合は、現時点で世界最速のコンピューターを使ったとしても、P×QからPとQの値を求めるのに何億年・何兆年とかかるそうです。）
図は[ＲＳＡ暗号について](http://www.comm.tcu.ac.jp/~math/hnakai/infomath/rsa.html)を参考に作成
従来では、この計算（暗号）を解くために、私たちの生きている以上の時間を有してしまうためにクレジット情報や口座情報などの安全性が担保されていましたが、ショアのアルゴリズムはこの暗号が解かれてしまうかもしれないと言われています。
ショアのアルゴリズムの詳細につきましては
量子コンピュータで因数分解が高速に解ける？〜 ショアのアルゴリズム 〜
に詳しく記述されております。
ここでは直感的にわかるように参考にした書籍に沿って説明します。
ショアのアルゴリズムの計算手順は（厳密ではありませんが）、以下の通りになります。
(1). 素因数分解したい数字をとってきます（yとする）
(2). 因数分解したい数より小さい数を適当に用意する（$x$とする）
(3). 2で選んだ数の1乗、2乗、3乗....と計算します（$x$,$x^2$,$x^3$,....）
(4). 3で得られた数字をそれぞれ1の素因数したい数字で割ったあまりを出します
(5). ここで面白いことに数字のパターンが存在します（周期が$T$とする）
(6). $z=x^{\frac{T}{2}}$を計算
(7). $z-1$,$z+1$とyの最大公約数をとるとそれが欲しい素数になる
一度に列挙してしまい申し訳ありませんでしたが、具体的に数を入れれば簡単に理解することができると思います。
たとえば素因数分解したい数を$y=15$、それより低い値で任意の値$x=7$と設定します。簡単な計算ですが、Pythonで表すと。
#素因数分解したい数を15
y=15
#それより低い値で任意の値を7
x=7
pattern_list=[]
#とりあえず16乗まで計算します
for i in range(16):
x_n=x**i
amari=x_n%y #あまりの計算
pattern_list.append(amari)
pattern_listに格納されたパターンは
[1, 7, 4, 13, 1, 7, 4, 13, 1, 7, 4, 13, 1, 7, 4, 13]
であることが確認できます。ここで周期Tが4（1,7,4,13の繰り返し）であることがわかるはずです。（厳密に周期がいくつであるかというのはなかなか難しい話ですが）
$z=x^{\frac{T}{2}}$を計算を計算し、z+1,z-1と素因数分解したい数字yの最大公約数を計算すると。
T=4 #周期
z=x**(T/2)
#z+1,z-1のとy=15の最大公約数を計算します
#最大公約数の計算は以下の関数で計算できます。（データ構造とアルゴリズムの勉強をされた方は当たり前だと思いますが）
#詳しくはhttp://cocodrips.hateblo.jp/entry/2014/03/05/143623
def gcd(a, b):
while b:
a, b = b, a % b
return a
#結果を出力
print(gcd(z+1,y))
print(gcd(z-1,y))
以上により3と5を求めることができます。（実際に3*5=15なのであってます）
今回はうまくいくようにわざと、素因数分解したい数字を15、それ以下の任意の数字を7をしましたが、実際一つずつ求めていくよりもこの方法により少し早く求まるらしいです
また、sympyというものをもう少し簡単に求められます。
インストール方法は以下の通りです
http://docs.sympy.org/latest/install.html
from sympy.physics.quantum.shor import shor
shor(15)
先ほどの7という数字は人為的にいれましたが、うまくいかないこともあるようです。なので、うまく素数が求まるかどうかは確率的に決まり、運が良ければ求まります。この計算では片方しか求まりませんが、片方が求まればもう片方も求めることができます。
運が良ければ
got lucky with rand
3
運が悪ければTypeErrorとなってしまいます。
以上がショアのアルゴリズムですが、これ方法でも大きな素因数では計算できません（この計算自体、量子コンピュータではなく私の手元のMacで計算したため）、この方法と量子の重ね合わせ状態と、量子フーリエ変換という操作から計算回路を作ることで初めて、1発で周期を求め、大きな数の素因数分解ができると理論的に言われています。（この辺は直感的ではなく、数式をたくさん記述しなければならないので割愛します。）
##グローバーのアルゴリズム
グローバーのアルゴリズムとは探索するアルゴリズム(例えば携帯の名前から電話番号を探索するようなもの）で、この法則により量子力学の法則を使えば、従来より高速に探索したい答えを求めることができると言われています。
グローバーのアルゴリズムについては、以下のサイトが実演も含め非常にわかりやすく説明されていましたので、以下の参考の図を用いて説明します。
IBM Quantum Computing で計算してみよう
従来の探索アルゴリズムではソートされている、電話帳などであれば、例えば"相原"さんなら電話帳の上の方にありますし、"和田"さんだと下の方にあるみたいに簡単に検索することができましすが、ソートできない場合を想定した場合に一つずつしらみつぶしに探していくと、最悪の場合、電話帳の最後に欲しい人の電話番号が見つかるということがあります。
https://www.ibm.com/developerworks/jp/cloud/library/cl-quantum-computing/index.html
100件ソートされていない電話帳なら100番目に見つけたいデータが見つかることがあるということです。ビッグ・オー記法でO(n)と表します。nはこの場合100で最悪の場合100番目という意味です。
電話帳やソートできるものであれば、ソートしたり、ほかのアルゴリズムでいいと思いますが、例えば「世界中の中から(70億人から)、お互い顔も性格も全てが合う、まさしく運命の人がこの世界に1人だけいる場合」を想定してください。（この辺の話は今度こそわかる量子コンピューター (今度こそわかるシリーズ)の13章に記載されております）
お互い実際会って、話した時に運命にひとかわかるとした場合で、最悪の場合は70億番目に最も適した運命の人に出会うことになります。
このような場合を想定した時でも、グローバーのアルゴリズムによればO記法でO($\sqrt{n}$)で計算できるようになります。
実際計算すると約83666人なのでだいぶ現実的な数字で探すことができるようです。
[図は全く関係ありませんが](https://miror.jp/press/column/844)
話は逸れましたが、一般に量子ビットは重ね合わせのおかげで、n個のビットで$2^n$個の状態を一度に表現できます。$2^n$で計算できるおかげで、実際に観測に必要な観測はO($\sqrt{n}$)ですむというのです。ただ、実際は測定すると重ね合わせ状態は壊れてしまうので、実際には量子ゲート回路と、折り返し量子回路というものを組み合わせて欲しい値の状態の確率振幅を大きくし、その結果、遅くてもO($\sqrt{n}$)で計算が完了するというのです。
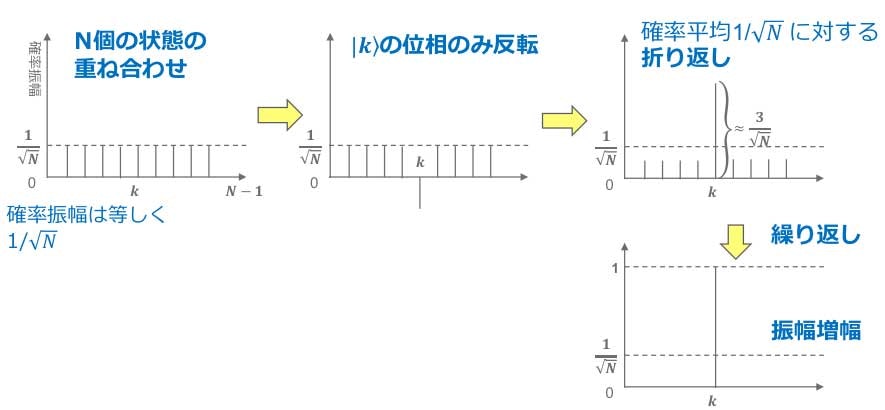
https://www.ibm.com/developerworks/jp/cloud/library/cl-quantum-computing/index.html
このO($\sqrt{n}$)を求める辺りから、線形代数や量子力学の計算知識（ブラ、ケットなど）が必要になります。私も自分でまだ計算していませんので、自分で計算してみて、余力があれば、計算結果も踏また記事などをかければと思っております。
#量子コンピューターの方式
現在様々な量子コンピューターの方式がありますが、大きく分けて量子ゲート方式と、量子アニーリング方式があります。【初心者向け】量子ゲート方式と量子イジングモデル方式の違いにて説明されているように、ショアのアルゴリズム、グローバーのアルゴリズムなどの量子アルゴリズムに沿って演算をする方式のことを、量子ゲート方式といい、イジングモデルという、物理モデルを解くことでそのエネルギーの最小値を求めることで、実際の最適化問題を解く方式のことを量子アニーリング方式と言います。
量子アニーリング方式については今回は扱っておりませんでしたが、、直感的な概要は、私が昨年書いた「量子コンピュータが人工知能を加速する」を読んで、数式を使わずにPythonでその概要を説明してみたに記載されておりますので、是非ご覧ください。
#最近の出来事
最近の研究では、量子ビット50個以上からなる量子コンピュータが、開発されておりさらなる研究開発が加速すると考えられます。（https://news.mynavi.jp/article/20171211-555233/）
また、2017年は、量子コンピュータの様々なツールが各社より発表されて
・IBMの誰でも使える量子コンピューター「IBMQ」
・Microsoftの量子コンピュータ言語「Q＃」
・googleの量子化学計算パッケージ「OpenFermion」
2018年以降も様々なツールが出るのではないかと期待しています。
#今後は（個人的な意見ですが）
量子コンピュータで興味深いのレビューが公開されておりました。量子コンピューターはもはや未来の夢のコンピューターではなく、近い将来、なにかしらの形で実現すると考えられます。競争が激しくなる量子コンピュータ開発の中で、日本も取り残されないようにしなくてはならないと思います。
記念特集 2-8 エレクトロニクス技術を変革する量子情報技術
開発が進むにつれて、現在では自動運転エンジニアが優遇されているのと同じように、機械学習、深層学習と量子コンピュータの融合、つまり、量子コンピューターとデータサイエンス両方の知識があるエンジニアが市場価値が活発化するのではないかと個人的に考えています。
#この先私が勉強したい資料や、勉強法
##記事、書籍
qiitaなどの記事（特に量子コンピュータ Advent Calendar 2017）をみて、記事を読みながら計算はもちろん、sympyやIBMQなど実際に自分で動かしてみる。
全体のまとめとして
・ITエンジニアのための量子コンピュータ入門
・概念誕生から35年、本格量子コンピュータ実現への道のり
など
数式は出てしまうが、わかりやすそうな教科書として
・今度こそわかる量子コンピューター (今度こそわかるシリーズ)
などがありました。
##授業、動画
日本語の講義ビデオとして
有料ですが以下の講座もございます
・量子コンピュータとは何か？(crash.academy)
##twitterで最新の動向をチェック
量子コンピューターの開発者や、研究者などをフォローして最新情報をキャッチアップすると色々な知見が得られると思っております。
##勉強会に参加してみる
都内が中心になってしまいますが、昨年から量子コンピューターについての勉強会が増えていて、募集されても開始直後に満員になっている状況です。この分野について、徐々に注目され始めていることがわかります。
なので、この分野に興味がある人は、自分で記事や書籍、動画で勉強する以外に、イベント管理しているcompassから勉強会に参加してみましょう。（募集開始後、一瞬で埋まってしまうので気をつけてください。また、早いもの順だからといって登録だけしておいて、当日行かなかったり直前でキャンセルするのは極力控えましょう。）
2017年12月25日現在で
・量子情報・量子コンピューターを学ぶ - OpenQL Project -
・量子情報勉強会
・量子コンピュータアプリ（ゲートモデル＆アニーリングモデル）
私も、来年は上記の勉強会にいくつか参加したいと考えております。
#最後に
いかがだったでしょうか、量子コンピューターは最近やっと注目されるようになってきましたが、量子力学という難解な学問を理解しなければいけないために大変だったと思います。最初はわからなくて当然だと思いますので、長い目でコツコツ勉強して行くことをお勧めします。
私は学生時代に量子系の研究をしておりましたが、ショアのアルゴリズムやグローバーのアルゴリズムについて無知だったので引き続き勉強していきたいです（恥ずかしながら「アダマール変換、なにそれ？ブラ・ケット懐かしい〜」って感じです（笑））。それと同時に、様々なツール（IBMQ、Q＃など）が公開されておりますので、自分でも色々動かして最新情報をどんどんキャッチアップしたいと考えております。