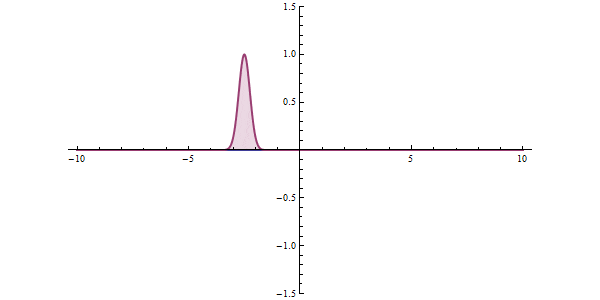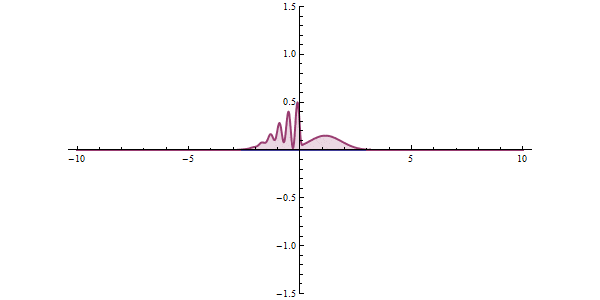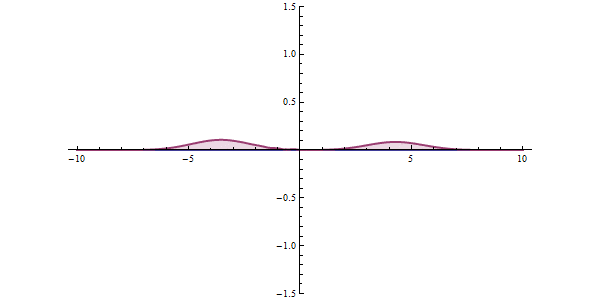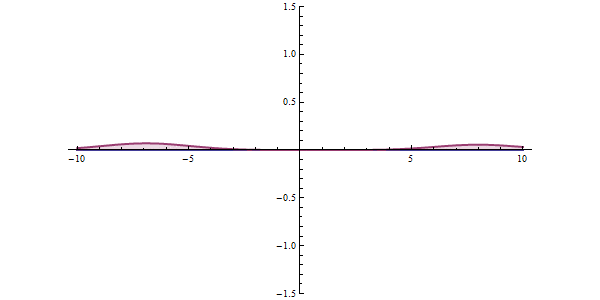本記事はWACUL Advent Calendar 2016の12/21の記事になります。
こんにちは、WACULのデータサインエンスチームで、データ分析の仕事をしている@onhrsです。
直近では自然言語処理やその他、機械学習にかかわるデータ分析のお仕事をやらせていただいています。
今回、西森秀稔先生、大関真之先生の量子コンピュータが人工知能を加速するを読みましたので、書籍の内容に沿う形で人工知能 × 量子コンピューターの実態についてお話ししたいです。(物理や数学がわからない人にも理解していただけることを目指しました。)
また、Pythonを使って、数式を使わずに概要を説明してみました。詳細がよくわからなくても、視覚的に見えるようにして理解できるように心がけました。
Advent Calendar以外で記事を投稿しようという意欲が出るため、是非、"いいね"してくれると嬉しいです。(笑)
本記事の対象者
・量子コンピューター、量子アニーリングについて知りたい方
・量子コンピューターの現状、将来性を知りたい方
・量子コンピュータと人工知能の関係を知りたい方
・Pythonでデータサイエンスに入門したい方
想定される環境
言語:Python3
NumPyやSciPy,matplotlibなど必要だが、Anacondaを入れれば大丈夫です。
エディター:Jupyter(もちろん他のエディターでもいいです。)
キーワードとして
難解な単語、聞きなれない用語が出てくると思います。予習と、後で見返すように重要単語、キーワードとその簡単な概要をここでまとめて紹介します。(この時点で理解できない言葉があっても大丈夫です。その時は読み飛ばしてください)
※順番は適当です。
※厳密な定義ではございません、むしろ分かりやすさを追求するあまり、嘘をついているところもございますが、そこは各自、理解した後で再構築してください。(笑)ちゃんとした理解をするためには、統計力学と量子力学の理解が必須です。
機械学習
こういう単語ほど簡単に説明するのが難しいのですが、要するに、統計的手法を用いて、そこから得られるパターンを見つけ出すことです。現在のビックデータ分析には欠かせない手法です。
深層学習(またはディープラーニング)
脳を模倣した方法(ニューラルネットワーク)を用いて、機械学習を行う手法のこと。
画像判定を始め、データがすごくある時に大活躍します。
※厳密には多層構造であることや、必ずしも深層学習がニューラルネットワークの構造である必要があるとは限りませんが…。
量子コンピューター
従来の'0'と'1'の二進数で演算をしていたコンピューターと違い、量子力学という、原子や分子など微視的(すごく拡大すること)な世界で生じる'波'の性質を使ったコンピューターのこと。
量子アニーリング
最適化問題という、すべての経路を計算していたらすごく時間のかかる計算を、上記の量子力学の波の現象を用いて高速に計算する手法のこと。量子焼きなまし法ともいう。
量子ビット
通常のビットは'0'と'1'しか表せないのに対し、量子ビットは上記で挙げたように、波なので、重ね合わせて表現することができます。1であり0でもあるという曖昧なものを表現できます。(詳しい内容は量子エンタングルを理解すればわかると思います。)
量子エンタングル
上記の重ね合わせの量子状態そのもののことです。
物質も量子の世界では波なので、重ね合わせられるので、その状態そのもののことです。(多分、こういう理解であっていると思います。)
※難しく言うと、二つの粒子(波)を考えた時に、相互に受ける相関の事で、片方の状態が決まれば、もう片方の状態も決まります。量子テレポーテーションはこの現象を用いています。
シミュレーティド・アニーリング
金属を高温にした状態で、ゆっくり温度を下げていくと、結晶構造が綺麗になる現象の「焼きなまし」から由来していて、結晶のエネルギーを最小にするこの手法を数値計算に置き換えて、最適化問題を古典的に解く方法です。
量子ゲート方式
量子ビットを半導体に組み込んで、演算させる方式のこと。従来の量子コンピュータといえば、むしろこっちの方式を指す場合が多かったが、量子アニーリングの量子コンピュータ出現によって、立場が逆転してしまった。
この量子ゲート方式の量子コンピュータは、量子状態は崩れやすくなかなかうまくいかなかった。
トンネル効果
量子状態では物質を波として考えられ、その波というものは確率的に決まる波であって、ある特定の状況で、エネルギーの障壁を乗り越えるのではなく、"すり抜ける"状況が起こります。
スピン
磁石の最小単位のことです。
電流の最小単位である電子は回転の性質を持っています。この回転することです。(上向き、下向き)とか(右回り、左回り)と表現します
~~そろそろ素粒子を専門にしている方に本気で怒られそうですが(笑)~~気にせず進みましょう
イジングモデル
量子アニーリングを実現するためのモデルで、上記のスピンのエネルギー状態を最小にする状態を最適化問題の解となるようにすることが可能。
D-Wave
量子アニーリングを提唱した、西森先生の理論を実用化し、世界で初の商用量子コンピュータを製作した企業。
スーパーコンピューターでも解けない巡回セールスマン問題について
巡回セールスマン問題を考えるにあたって、あるセールスマンが、複数の都市を巡回するときに最も距離が最小になる経路を考えます。
例えば3つの都市(例えば東京と名古屋と大阪)は
東京→大阪→名古屋→東京と東京→名古屋→大阪→東京ですが、
逆向きに巡るのは同じものとみなすらしいので、3つの都市の場合は1です。

[量子コンピュータ1]突然商用化した夢のマシン (3/6)より抜粋
一般化すると
\frac{(n-1)!}{2}通り
です。
なのでPythonで書くと(わざわざ書く必要もないと思いますが)
# 巡回セールスマン問題
import math
def travelingSales(n):
return math.factorial(n-1)/2
これを使って、
8都市なら
travelingSales(8)
2520
15都市なら
travelingSales(15)
43589145600.0(453億)
20都市なら
travelingSales(20)
6.0822550204416e+16
30都市なら
travelingSales(30)
4.420880996869851e+30
…
となります。
20都市までなら、スーパーコンピュータで数秒で解いてくれますが、30都市だと1400万年と時間がかかりすぎてしまいます。
以上が巡回セールスマン問題の概要になります。
参考 :[量子コンピュータ1]突然商用化した夢のマシン:ITpro
それではどのようにすればいいのか
実際の所、上記の問題を解くために様々な近似を計算する方法はいくつかありますが、量子アニーリングに関係ある、シミュレーティド・アニーリングに的を絞って説明します。
まず、現状を端的に整理すると、人間が見れば、単純な最短経路なんて見ればわかりそうですが、コンピューターはわざわざ全ての経路の組み合わせを考慮した上で最短経路を計算しなればならないために、仮に都市が30ほどでもその経路自体は無数に存在するために解くことはできないものでした。
具体的な例を説明するために、Scipyの公式ドキュメントを参考にして解説します。
「最適化問題とは、最小値や等式の数値解を見つける問題のことです。
scipy.optimize モジュールは関数の(スカラーや多次元)関数の極小化や曲線の曲線のフィッティング,
そして根の探索ための便利なアルゴリズムを提供しています。」(公式ドキュメントより)
最適化問題をBFGSアルゴリズムを使ったoptimize.fmin_bfgsを用いてプロットし、実際に計算します。
以下の関数を定義して、実際に最適化問題を解いてみます。
f(x)=x^2+15sin(1.2x) \\ (-10\leqq x\leqq10)
from scipy import optimize
def minfunc(x):
return x**2+ 15*np.sin(1.2*x)
x = np.arange(-10, 10, 0.1)
plt.plot(x, minfunc(x))

optimize.fmin_bfgs(関数,初期値,disp=0)とすればいいので簡単に求まって、
# disp=0で最小値だけ出す
optimize.fmin_bfgs(minfunc, 0,disp=0)
得られる値は
array([-1.19776296])
確かに目視でもわかるような最小値が得られました。
しかし、optimize.fmin_bfgsの2つ目の引数に仮に
# 初期値をx=-5に設定
optimize.fmin_bfgs(minfunc, -5, disp=0)
array([-5.94383045])
# 初期値をx=3に設定
optimize.fmin_bfgs(minfunc, 3, disp=0)
array([ 3.58552219])
# 初期値をx=10に設定
optimize.fmin_bfgs(minfunc, 10, disp=0)
array([ 8.20653212])
とすると、上記のようになってしまいます。
初期値から微分係数が0(決められた場所からボールを転がしたら凹みにトラップされる場所)の時のyの値しか求めることができません。

巡回セールスマン問題に当てはめると、先ほどのグラフの縦方向を都市を巡回した距離、横軸を都市を巡回するパターン数だと仮定すると(少し強引な気がしますが)、$(-10\leqq x\leqq10)$の全てで、optimize.fmin_bfgsを例にとり、様々な初期値で試して、その中で最も値が低いものを最小値(つまり都市を巡回した距離の最小値)となるのです。
しらみつぶしに探したら、結局のところ、巡回セールスマン問題のように30パターンもの量になってくるとなかなか解くことができなくなってしまします。
以上の問題を解くため、シミュレーティド・アニーリングという手法があります。
シミュレーティド・アニーリングでは、確率的な分布をもたせて、その分布をはじめは大きくとってから、徐々に確率の分布を狭めるため(この作業が、従来の"焼きなまし"の温度を徐々に下げる部分に該当するのだと思う)に、上記の例でトラップされたまま(微分係数が0)のものも、その時点で計算を終えずに最終的な最小値を探しに行きます。
しかし、このやり方でも、しらみつぶしに計算することよりは計算が少なくなるようですが、複雑な問題の場合、膨大な計算量を強いられることになりますし、トラップを脱出するために、大きなエネルギーを必要とします。
 <左の図が一般のシミュレーティド・アニーリング、右が量子アニーリング効果>
<左の図が一般のシミュレーティド・アニーリング、右が量子アニーリング効果>
これを量子アニーリングでは量子現象であるトンネル効果によって解決します。
シミュレーティド・アニーリングの確率的な探索に加えて、量子状態である波で探索することによって、トラップされた位置からトンネル効果を起こして簡単に最小値まで移動することができるのです。
以上のようにして、従来のシミュレーティド・アニーリングに量子の効果を用いることによって、巡回セールスマン問題などの計算を可能にすることができるようです。(「量子コンピュータが人工知能を加速する」の中には"一億倍"になると書いてありました。)
※トンネル効果はある条件を満たすと確率的に粒子の波が染み出すというもので、そう簡単に、トンネルして最適解に落ちるということは考えにくいが、なぜそうなるのかということは、個人の宿題として、後日調べたいと考えています。
実際に量子アニーリングを可能にするイジングモデル
では、実際に、量子アニーリングを可能にする状況下で、最適解を解くモデルとして"イジングモデル"というものがあります。
原子サイズで見た時に、磁石の最小単位であるスピンという性質が出てきます。実際は小さいしバラバラなので普段は見えないのだが、ある特殊な状態でスピンが揃い、その結果として磁石としての性質が生まれます。(※磁石の分野である"磁性"という学問はめちゃくちゃ難しい!!)
このスピンという性質は上向きと下向きの2つの状態しかもてません。(知っている人に言えば、量子化された状態のエネルギー状態は、離散的な値しか取れません。)
この小さい時に見える"スピン"という性質を用いて、計算するモデルがイジングモデルです。(相互作用の話やイジングモデルを計算する式自体は難しいので省きます。)
ここまでの説明で何を言っているのかわからないと思うので、具体的に見てみましょう。
計算を簡単にするためには、次元を減らして、2次元で議論します。(要するに、奥行きのないアニメの世界で議論しようということ。)
元ネタはIsing Modelを平易に解説してみる
とMonte Carlo Simulation of the Ising Model using PythonにPythonでイジングモデルを実装しているので、そちらを参考にして(特に、前者のコードを解説と改良しました。)
アニメーションにするために、matplotlibのArtistAnimationを使って配列imsに複数のイメージを記録してそれをArtistAnimationで実際に動かしています。
http://qiita.com/yubais/items/c95ba9ff1b23dd33fde2
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from pandas import Series, DataFrame
from numpy.random import randint, randn, rand
import math
import matplotlib.animation as animation
# Jupyter上でmatplotlibのアニメーションを再生する
%matplotlib nbagg
# 原子の数
Size = 50
# Jはスピン間の相互作用を表す定数
J = 1
# 磁場
H = 0
# 温度[K]
Temp = 0
# スピンが反転するか
def spin_direction(field, x, y):
energy = H
'''
周期的境界条件
(端っこに位置している原子は4つの原子に接していないために、
その場合のみ並行移動している。)
'''
for dx, dy in [(-1,0), (1,0), (0,-1), (0,1)]:
if x + dx < 0:
dx += Size
if y + dy < 0:
dy += Size
if x + dx >= Size:
dx -= Size
if y + dy >= Size:
dy -= Size
#エネルギー計算
energy += J * field.iloc[x + dx, y + dy]
if Temp == 0:
#np.signは各要素について、正の場合1、負の場合-1、ゼロの場合は0を返す。
p = (np.sign(energy) + 1) * 0.5
else:
#スピンが温度とエネルギーで反転する確率(T=0の時は除いている)
p = 1/(1+np.exp(-2*(1/Temp)*energy))
#上記で計算したスピンが反転する確率が0〜1の浮動小数点の乱数より上かどうか
if rand() <= p:
spin = 1
else:
spin = -1
return spin
# ギブスサンププリングについてはあんまりわかっていません。
def run_gibbs_sampling(field, iternum=5):
for _ in range(iternum):
lattice = DataFrame([(y,x) for x in range(Size) for y in range(Size)])
#reindexはindex振りなおす、適当に原子の位置を取るようにする
lattice = lattice.reindex(np.random.permutation(lattice.index))
#lattice.valuesは各格子点の位置。例えば、[0,0]であれば縦に0番目、横に0番目
for x, y in lattice.values:
#スピンが反転するか計算
field.iloc[x, y] = spin_direction(field, x, y)
fig = plt.figure()
field = DataFrame(randint(2,size=(Size,Size))*2-1)
temps = [0.,.5,1.,1.5,2.,2.5,5.0,10.0][::-1]
ax1=fig.add_subplot(1,2,1)
ax2=fig.add_subplot(1,3,3)
ax2.axis(xmin=-1,xmax=10.5)
ax2.set_xlabel("time")
ax2.set_ylabel("T[K]")
ims = []
for i in range(1,9):
Temp = temps[i-1]
run_gibbs_sampling(field)
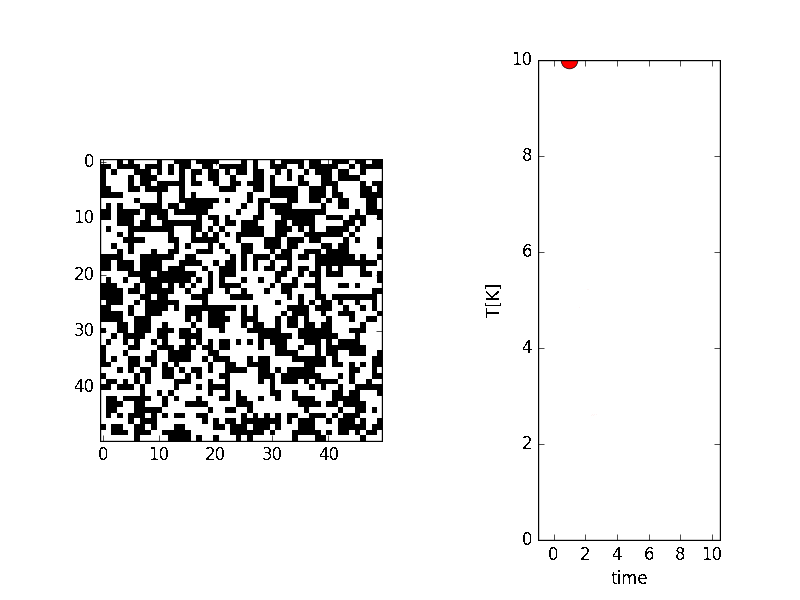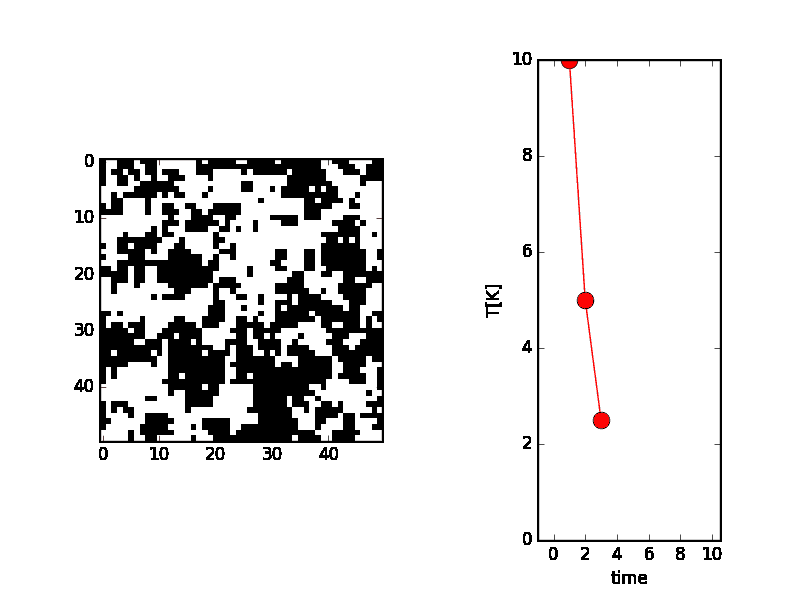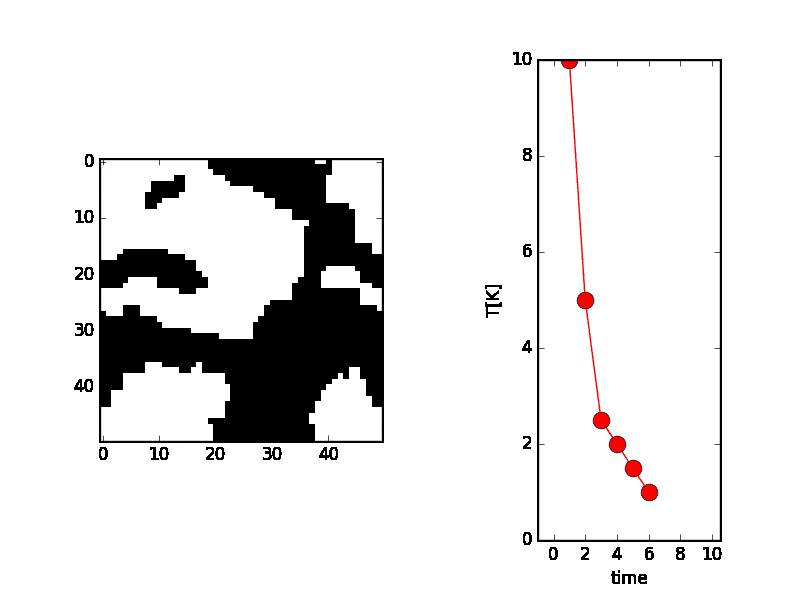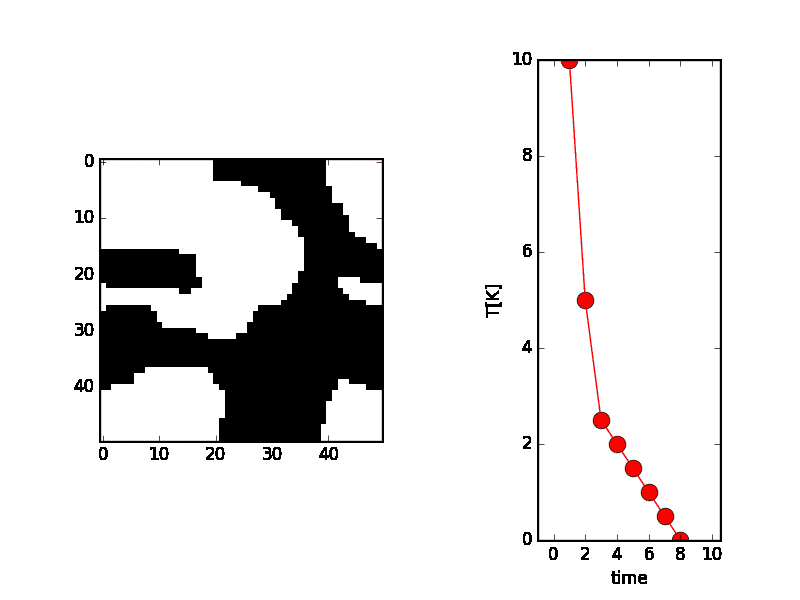
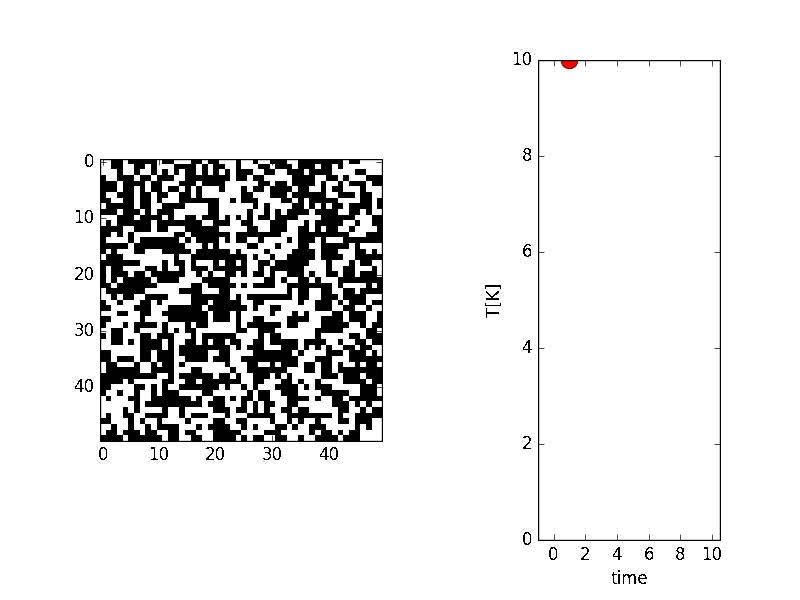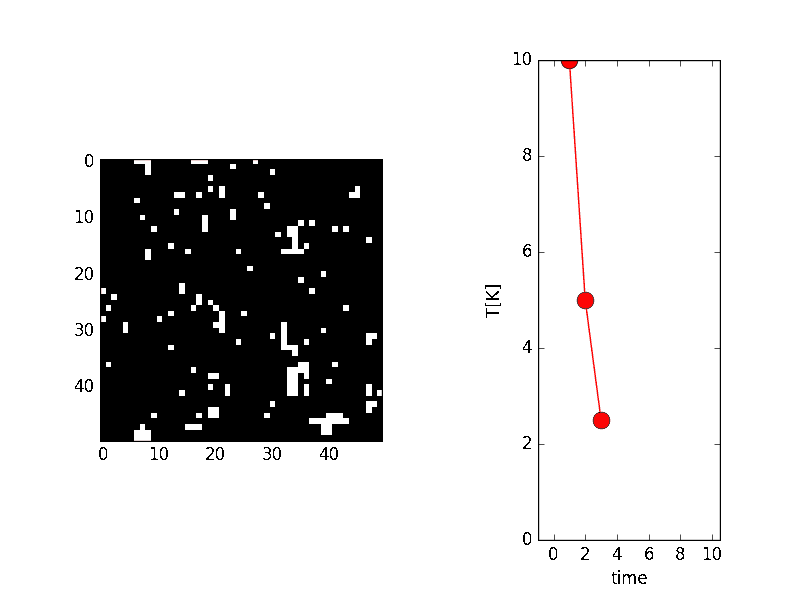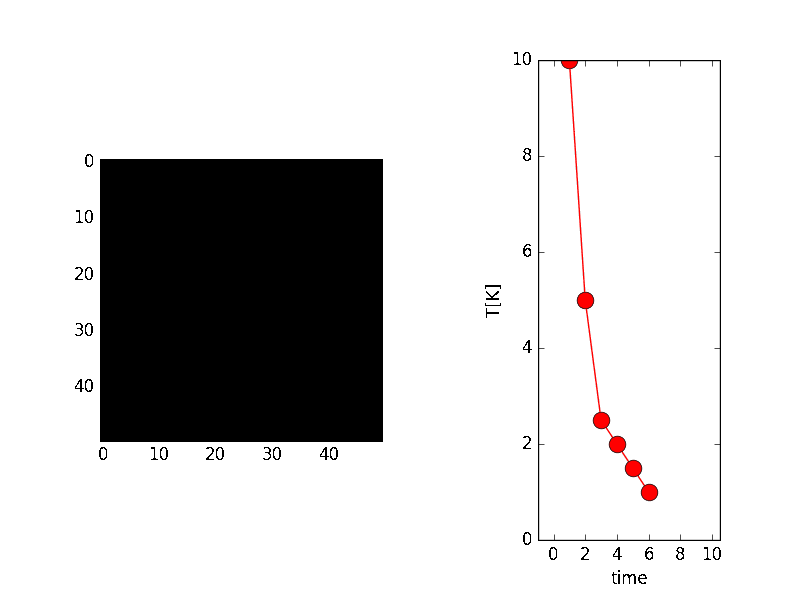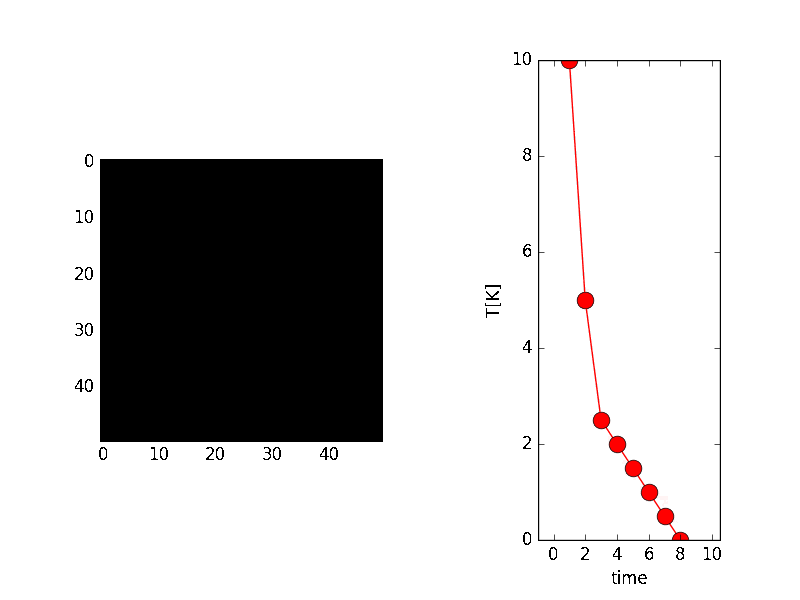
im1 = ax1.imshow(field.values, vmin=-1, vmax=1,cmap=plt.cm.gray_r, interpolation='nearest')
x=np.arange(1, 9, 1)
im2,=ax2.plot(x[0:i], temps[0:i],marker="o",markersize=12,color = "red")
ims.append([im1,im2])
ani = animation.ArtistAnimation(fig, ims, interval = 1000)
# 保存先(必要であれば)
# ani.save("ising.gif")
plt.show()
温度が0K(絶対温度と言って−273.15${}^\circ\mathrm{C}$を0Kとする)に近づくにつれて、バラバラだったスピンの状態が、安定状態(つまりエネルギーの低い状態)になって、上向きと下向きが局在した形になる様子が伺えます。
本当の安定状態は、すべてが上向きか、下向きなのですが、確率的にバラバラ(正確に言えば、温度による原子の振動によってバラバラ)であったために、温度が低くなった時にたまたま、隣り合ったスピンは同じ向きを向く性質があるために、一部は局在したものとなっております。
※スピンの相互作用はJの大きさで決まってきます。
磁場をかけた場合(磁石を近づけた場合を想定していただければいいです。)は(上記のコードにH=0.5)で実行するだけでいい。
こちらは磁場の力によってT=2K付近で全て同一方向を向いたものとなる。
さっきのように、たまたま局在していたものも、磁場のアシストによって、局在する前に全て同一方向に向く様子がわかります。
ここまでで、2次元のインジングモデルについての解説でした。(長かった。)
このモデルに従い、実際に物質のスピンの安定した状態を最適化問題応用したものが量子アニーリングになります。
実際の量子コンピューターは、上記のイジングモデルを3次元に拡張したものです。
このモデルに拡張しても、スピンは不思議なことに上向きと下向きの2つの状態しか持ちません。
イジングモデルを3次元に拡張した物質に、横から磁場をかけることで、スピンの上向きと下向きの重ね合わせ状態(量子エンタングル状態)を作ります。
先ほど、温度を下げたのと同様にして、この横磁場を徐々に下げていくと、原子間のスピンの相互作用が大きくなり、横磁場が0の時のスピンのエネルギー状態が解きたい最小値を取るというのです。
以上のようにして、スピンの重ね合わせ(量子エンタングル)状態を実際の物質で行うことで、シミュレーティド・アニーリングでも、膨大な計算量が求められた最適化問題を、量子の現象(特にトンネル効果)によって実現しているのです。
自分で図を描こうとしましたが、力尽きました。詳しくは先ほども紹介したサイトで。(あとで編集して更新するかも)
http://itpro.nikkeibp.co.jp/article/COLUMN/20140514/556566/
機械学習、ディープラーニングとの関わりとか?
機械学習や深層学習(ディープラーニング)の分野でも応用が期待されていて、投資のポートフォーリオの最適化問題、画像認証、医療、法律、考古学など、近年急激に発展してきたAI(ないしは機械学習)の分野にも、今回の量子コンピュータはそれらを加速させることができそうです。また、D-waveの出現によって、googleがこの方式での本気で量子コンピューターを実現しようとしていることなど、量子アニーリングによる応用分野は非常に多岐に渡ると言えます。(この辺りの詳しい内容は西森先生の「量子コンピュータが人工知能を加速する」を是非参照してください。)
終わりに
後付けですが、私自身現在は、データサイエンティストとしてAI(機械学習、ないしは統計学のことですけどね)を用いてビックデータ(主にwebのデータ)の分析の仕事をしておりますが、大学院では、スピントランジスタという、量子ゲート方式の量子コンピューターを実現する素子の研究をしていました。
当時関係ないと思われていた、AIと、量子コンピューターが、近年では関わりを持ち始めており、真のAIの実現に量子コンピューターが重要な役割を担っているということは驚きでした。(大学の研究が無駄にならなかった。)
また、量子力学やイジングモデルなどまだまだ本当に奥が深く、これを機にもっと勉強しようと思いました。(今なら当時挫折したランダウの統計物理学を読めるはず。(笑))
スピンや量子力学や統計力学はミクロの世界を論じる学問であり、1日、2日でわかるはずがありません。これを機に、色々と勉強すれば、面白さや注目度がわかるはず。(元に、今回の本がamazonの物理のカテゴリーで1位になっていました。)
※個人の課題として
・トンネル効果よって、従来のシミュレーティド・アニーリングよりも簡単に最適解に行ける厳密な概要。
・ギブスサンププリングについて
以上のことを理解してまた記事を書きたいです(笑)
また、明らかな間違い、疑問点がございましたら是非教えてください。修正いたします。