重心を考慮して長方形を配置していきたい(訂正)
Q&A
先日質問させていただいてたコードや質問内容に誤りがあったためもう一度まとめなおさせていただきます。
解決したいこと
箱の左下から長方形を配置していくBottom-Left法を適応していく中で、長方形に重心を考慮して配置していきたいです。
今回は底辺の中心が他の長方形か箱の底辺に接していることを条件に積み上げていきます。
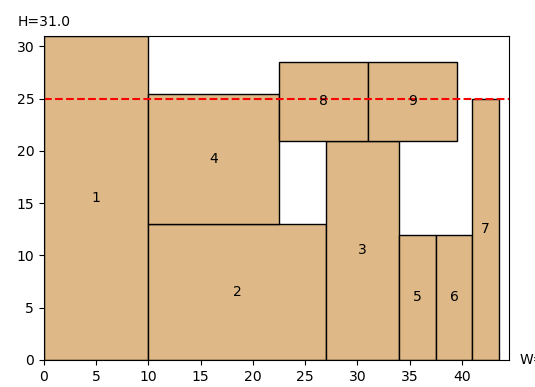
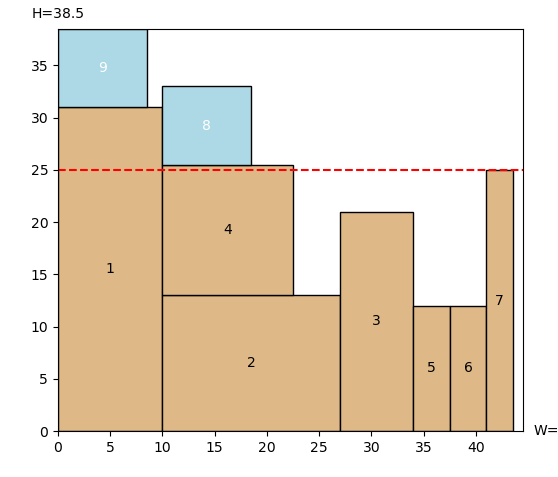
下の二つの図は8と9は中心が触れていないので次のBL点を探して配置されていることを表しています。
やりたいこと
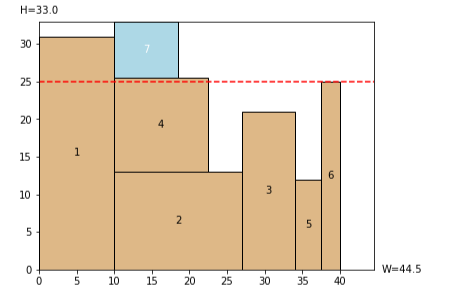
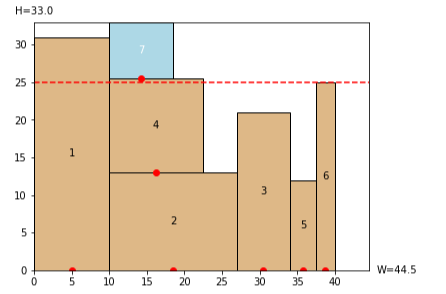
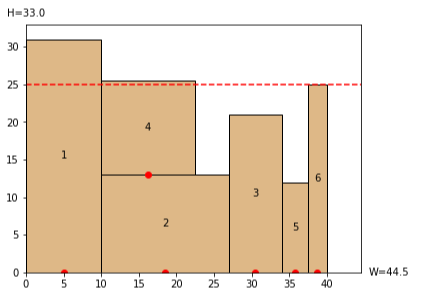
下図の7を配置する際、4に触れる形で3の上に配置しようとするのですが底辺の中心が触れていないため別のBL点を探して4の上に配置されています。この7を、6に接するように3の上に置く(底辺の中心は触れている)ことはできないでしょうか?赤点線を超えて配置をすると青色になるのですが、あまり青色を出したくありません。アドバイスをいただきたいです。
手順
配置する長方形はエクセルからランダムで持ってきます。持ってくる条件は重心を考慮しないで配置する際、底辺が赤線を超えないような数を持ってきています。
全コード
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import pandas as pd
import csv
import tkinter
import time
import numpy as np
import openpyxl
import random
# ファイルを開く
filename = "実行結果final2.xlsx"
workbook = openpyxl.load_workbook(filename)
# 利用可能なシート名のリストを取得
sheet_names = workbook.sheetnames
# ランダムにシートを選択
selected_sheet_name = random.choice(sheet_names)
sheet = workbook[selected_sheet_name]
# シートのデータを読み取る
data = []
for row in sheet.iter_rows(values_only=True):
data.append(row)
import pandas as pd
df = pd.DataFrame(data[1:], columns=data[0])
df
def intersection_NFP(p, q):
if q[0][0] < p[0][1] < q[0][1] and p[1][0] < q[1][1] < p[1][1]:
return (p[0][1], q[1][1])
if p[0][0] < q[0][1] < p[0][1] and q[1][0] < p[1][1] < q[1][1]:
return (q[0][1], p[1][1])
return False
#p=[(x1,x2),(y1,y2)] NFPとx軸の交点を求め、 BL点候補点とする。
def intersection_x(p):
if p[0][0] < 0:
return (0, p[1][1])
return False
#p=[(x1,x2),(y1,y2)] NFPとy軸の交点を求め、 BL点候補点とする。
def intersection_y(p):
if p[1][0] < 0:
return (p[0][1], 0)
return False
#p=(a,b) q=[(x1,x2),(y1,y2)] 点pが領域q内に含まれているか、いないか。(境界線は含まない)
def include_p(p, q):
return q[0][0] < p[0] < q[0][1] and q[1][0] < p[1] < q[1][1]
#p=(a,b) q=[(x1,x2),(y1,y2)] 点pが領域q内に含まれているか、いないか。(境界線は含む)
def include_p_e(p, q):
return q[0][0] <= p[0] <= q[0][1] and q[1][0] <= p[1] <= q[1][1]
#p=(a,b) q=[{(x1,x2),(y1,y2)},{(x3,x4),(y3,y4)},...]
#点pが領域配列qのいずれか1つに含まれているか、いないか。(境界線は含まない)
def include_p_n(p, q, n):
for i in range(n):
if include_p(p, q[i]) == True:
ans = True
break
ans = False
return ans
class Rect:
def __init__(self, x, y, w, h, weight,name):
self.x = x
self.y = y
self.w = w
self.h = h
self.weight=weight
self.name=name
#未配置の長方形jの高さhb横幅wb配列 既に配置されている長方形iの高さha横幅ba配列
def NFP(self, b):
return [(self.x-b.w, self.x+self.w), (self.y-b.h, self.y+self.h)]
#箱の中に収まる範囲 UBはHの上界値
def include_room(self, W, H):
return [(0, W-self.w), (0, H-self.h)]
#長方形nにおいて既存に配置されている長方形とのNFPを計算
def NFP_r2(self, rects_after):
cand = []
if not rects_after:
return cand
else:
for rect in rects_after:
p = Rect.NFP(rect, self)
cand.append(p)
return cand
#p=(a,b) [(x1,y1),(x2,y2),...(xn, yn)] 求めたBL候補点pが既に使われていないか。
def point_search(rects_after, p):
for rect in rects_after:
if p[0] == rect.x and p[1] == rect.y:
return True
return False
#既存にm個の長方形が配置されている状態に長方形nのBL点を求める
def BL_method(self, rects_after, W, UB):
if not rects_after:
return (0, 0)
BL_point = []
#print(f'{n}')
#print((w[n],h[n]))
a = self.NFP_r2(rects_after)
#print(a)
m = len(rects_after)
for i in range(m):
if not intersection_y(a[i]) == False \
and include_p_e(intersection_y(a[i]), self.include_room(W, UB)) == True \
and Rect.point_search(rects_after, intersection_y(a[i])) == False:
BL_point.append(intersection_y(a[i]))
if not intersection_x(a[i]) == False \
and include_p_e(intersection_x(a[i]), self.include_room(W, UB)) == True \
and Rect.point_search(rects_after, intersection_x(a[i])) == False:
BL_point.append(intersection_x(a[i]))
for j in range(i):
if not intersection_NFP(a[j], a[i]) == False \
and include_p_e(intersection_NFP(a[j], a[i]), self.include_room(W, UB)) == True \
and Rect.point_search(rects_after, intersection_NFP(a[j], a[i])) == False:
BL_point.append(intersection_NFP(a[j], a[i]))
BL_point = sorted(BL_point, key=lambda t:t[0])
BL_point = sorted(BL_point, key=lambda t:t[1])
#print('BL候補点')
#print(BL_point)
for BL in BL_point:
if include_p_n(BL, a, m) == False:
#中心の底辺を計算
bottom_center_x = BL[0] + self.w / 2
bottom_center_y = BL[1]
#他の長方形との重なりチェック
overlap = False
for rect in rects_after:
if rect.x <= bottom_center_x <= rect.x + rect.w and \
rect.y <= bottom_center_y <= rect.y + rect.h:
overlap = True
break
#箱の境界との重なりチェック
if bottom_center_x == 0 or bottom_center_x == W or \
bottom_center_y == 0 or bottom_center_y == UB:
overlap = True
if overlap:
p = (BL[0], BL[1])
return p
n=len(df)
W=44.5
sort_key="weight"
h = df['高さ'].values
print('高さ')
print(h[:n])
print('--------------------')
w=df['横幅'].values
print('横幅')
print(w[:n])
print('--------------------')
weight= df['重さ'].values
item=np.ones(n,dtype="int8")
print(item)
name=df['名前'].values
before_list = []
for i in range(len(item)):
for j in range(item[i]):
before_list.append((w[i], h[i], weight[i],name[i]))
n = len(before_list)
print('before sort')
print(before_list)
print('--------------------')
# UB=sum(h[i] for i in range(n))
UB=n*max(h)
rects_before=[]
for i in range(n):
new_rect = Rect(None, None, before_list[i][0], before_list[i][1],before_list[i][2],before_list[i][3])
rects_before.append(new_rect)
rects_before = sorted(rects_before, key=lambda t:t.h, reverse=True)
rects_before = sorted(rects_before, key=lambda t:t.w, reverse=True)
rects_before = sorted(rects_before, key=lambda t:t.weight, reverse=True)
print('配置前')
for rect in rects_before:
print(rect)
start = time.time()
rects_after = []
for rect in rects_before:
BL_point = Rect.BL_method(rect, rects_after, W, UB)
rect1 = Rect(BL_point[0], BL_point[1], rect.w, rect.h ,rect.weight,rect.name)
rects_after.append(rect1)
print('-----------------')
print('配置後')
for rect in rects_after:
print(rect)
H = max(rects_after[i].y+rects_after[i].h for i in range(n))
print(f'H={H}')
elapsed_time = time.time() - start
print("実行時間 = {:.3f} (秒)".format(elapsed_time))
%matplotlib inline
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(111,aspect='equal')
ax.set_xlim ([0,W])
ax.set_ylim ([0,H])
name = 0
for rect in rects_after:
name = name + 1
#ax.text(rect.x+rect.w/2, rect.y+rect.h/2, f'{name}', horizontalalignment="center", verticalalignment="center")
#rect1 = plt.Rectangle((rect.x,rect.y),rect.w,rect.h,fc="burlywood",ec="black")
#ax.add_patch(rect1)
if rect.y <= 24.9:
ax.text(rect.x+rect.w/2, rect.y+rect.h/2, f'{name}', horizontalalignment="center", verticalalignment="center")
rect_color = 'burlywood'
else:
ax.text(rect.x+rect.w/2, rect.y+rect.h/2, f'{name}', horizontalalignment="center", verticalalignment="center", color='white')
rect_color = 'lightblue'
rect1 = plt.Rectangle((rect.x,rect.y),rect.w,rect.h,fc=rect_color,ec="black")
ax.add_patch(rect1)
ax.plot(rect.x + rect.w / 2, rect.y, 'ro')
ax.text(0, H+1, f'H={H}', horizontalalignment="center")
ax.text(W+1, 0, f'W={W}', verticalalignment="center")
ax.axhline(y=25, color='red', linestyle='--')
# ...(プロットに関する他のコード)
plt.show()
試してみたこと
前回の質問でアドバイスいただいたUBの値に制限をかけるものですが試しにUB=32にしたところ以下のようになりました。
TypeError Traceback (most recent call last)
Input In [13], in <cell line: 183>()
183 for rect in rects_before:
184 BL_point = Rect.BL_method(rect, rects_after, W, UB)
--> 185 rect1 = Rect(BL_point[0], BL_point[1], rect.w, rect.h ,rect.weight,rect.name)
186 rects_after.append(rect1)
188 print('-----------------')
TypeError: 'NoneType' object is not subscriptable
ランダムでデータを持ってきているのでエラーが出るときと出ない時があります。高さが32を超えた長方形が表示されないです。よろしくお願いします。