サイコロの出目(全6面、各面の出現確率は均等に$\frac{1}{6}$)の様な乱数発生装置の分布を一様分布といいます。これが連続する場合の定義域xと値域y=f(x)の関係は以下。
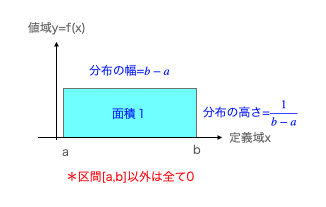
f(x)=
\left\{
\begin{array}{ll}
0 & (x<a) \\
\frac{1}{b-a} & (a≦x≦b) \\
0 & (x>b)
\end{array}
\right.
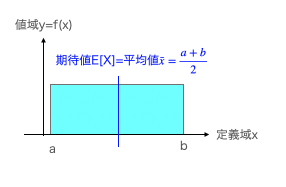
連続一様分布の期待値(平均)
平均(Mean)概念$\frac{a+b}{2}$には「真ん中だから全部足して2で割る」流のヒューステリックな解でも何とか到達可能ですが、後が続きません。
そこであえて$F^{\prime}(x)=f(x)$の場合における定積分の公式
\int_a^b f(x)dx=\left[F(x)\right]_a^b=F(b)-F(a)
を用いてきっちり解くと以下の様になります。
LoT用語辞典「ヒューステリック」
高校数学の美しい物語「一様分布の平均,分散,特性関数など」
E[X]=\int_a^b xf(x)dx=\int_a^b \frac{x}{b-a} dx
- ここで期待値の線形性E[aX]=aE[X]と冪算の積分公式$\int x^n dx=\frac{x^{n+1}}{n+1}$を用いて
\frac{1}{b-a}\left[\frac{x^2}{2}\right]_a^b=\frac{1}{b-a}(\frac{b^2-a^2}{2})
=\frac{1}{b-a}(\frac{(b+a)(b-a)}{2})=\frac{a+b}{2}
この考え方を用いれば分散(Variance)概念に連続してアプローチ可能となります。
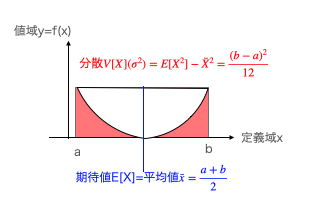
連続一様分布の分散
ここでは平均$\bar{x}を用いて$分散$V[X]=σ^2$を求めるのに公式$\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2$ではなく「二乗の平均と平均の二乗の差を求める」公式$E[X^2]-\bar{X}^2$の方を使います。とはいえ後者は前者を単純に変形した結果に過ぎません。
高校数学の美しい物語「分散の意味と2通りの求め方・計算例」
V[X]=E[(X-\bar{X})^2]=E[X^2-2X\bar{X}+\bar{X}^2]
- ここで期待値の線形性E[a+b]=E[a]+E[b],E[aX]=aE[X]を用いて
=E[X^2]-2E[X]\bar{X}+\bar{X}^2=E[X^2]-2\bar{X}^2+\bar{X}^2
=E[X^2]-\bar{X}^2
この公式を当てはめると…
高校数学の美しい物語「一様分布の平均,分散,特性関数など」
V[X]=E[X^2]-\bar{X}^2=\int_a^b x^2f(x)dx-(\frac{a+b}{2})^2
- ここで平均の場合同様に左項の定積分を解きつつ右項を展開し、かつ左項も三次式の公式$a^3-b^3=(a-b)(a^2+ab+b^2)$を用いて展開し、約分する。
=\frac{1}{b-a}(\frac{b^3-a^3}{3})-\frac{a^2+2ab+b^2}{4}
=\frac{1}{b-a}(\frac{(b-a)(b^2+ba+a^2)}{3})-\frac{a^2+2ab+b^2}{4}
=\frac{a^2+ab+b^2}{3}-\frac{a^2+2ab+b^2}{4}
=\frac{(4a^2+4ab+4b^2)-(3a^2+6ab+3^2)}{12}
=\frac{b^2-2ab+a^2}{12}=\frac{(b-a)^2}{12}
ここで$b^2-2ab+a^2$を$(b-a)^2$とも$(a-b)^2$とも変換可能なのが要注意ですね。そして標準偏差$σ=\frac{b-a}{2\sqrt{3}}$となります。
「ガウスの誤差関数」成立時点における分散概念の意味
こうして分散(Variance)の計算過程に注目するとその幾何学的意味合い(円錐座標系における位置付け)が浮かび上がってきたりします。
【Token】円錐座標系

そして分散V[X]$(σ^2)$の式形$E[X^2]-\bar{X}^2$から、以下の事がわかります。
- もし観測データXの値が均質ないしはそれに準ずる状態の場合($E[X^2]≒\bar{X}^2$)、分散V[X]$(σ^2)$の値は限りなく0に近付く。
- ほとんどのデータがこの状態にあるのに、特定のデータだけこの基準から際立って外れていてそのせいで分散幅がむやみやたらと大きくなっている場合、このデータを「外れ値」として除去する事によって上掲の状態に近付ける事ができる。
ガウスが当初誤差関数(ERF=ERor Fuction)概念に到達したのは「外れ値」に弱い最小二乗法の欠陥を補う為でした。要するに当初の目的はある種の「手ブレ除去」だったのです。
【数理的溢れ話12パス目】数聖ガウス「ムッツリスケベは濡れ衣」
- 乱数による「手ブレ」シミュレーション(n=2)

- 乱数による「手ブレ」シミュレーション(n=15)

- 乱数による「手ブレ」シミュレーション(n=30)

- 乱数による「手ブレ」シミュレーション(n=1200)

まるで(逃げ回る)卵子に群がる精子…数に任せて包囲網を狭め、最後は完全に逃げ場をなくす感じ? 中心極限定理(CLT=Central Limit Theorem)をまざまざと実感する好例といえましょう。
統計Web「17-3. 中心極限定理1」
さてかかる「手ブレ除去作業」、それまでの時代の観測者達は「それぞれがそれぞれの基準に従って好き放題に」遂行してきた訳ですが、ガウスはそのままではいつまで経っても観測精度(Observation Accuracy)が上がらないと考え、
- 小さな誤差ほど比較的観測され易い。
- 大きな誤差ほど比較的観測され難い。
- その分布は概ね以下の式で計算される。
erf(x)=\frac{1}{π}\int_0^xe^{-x^2}dt
と提唱したのでした。いわゆる「信頼区間(Confidence Interval)」概念の嚆矢であり、そもそも「全観測者が外れ値を切り捨てる基準を共有する事によって観測精度を引き上げる」計画の発想自体が天才的で、かつその分布認識も、(当時の制度における)観測の対象が天体や自然現象の様にある種の「絶対的単一性(Absolute Unity)」が期待し得る場合には必要にして十分という感じだったのです。
統計Web「19-3. 95%信頼区間のもつ意味」
ベータ分布やベータ関数との連続性
ところで、連続連続一様分布は$F^{\prime}(x)=f(x)$の場合においてF(x)=x,f(x)=1と書き表す事が出来ます。そして関数f(x)=1を定積分した結果得られる「b-a」をルベール測度(Lebesgue measure)と呼びます。
\int_a^b f(x)dx=\left[1\right]_a^b=b-a
①閉区間[a,b]の一次元ルベーグ測度はb−aである。
②開区間(a,b)の一次元ルベーグ測度も閉区間との差集合(つまり両端点のみからなる二元から成る集合 {a, b})の測度が0であることから、同じくb−aである。
③二次元集合Aが、一次元区間[a,b]と[c,d]の 直積集合(つまり辺が軸に平行な長方形)であれば、Aの二次元ルベーグ測度は、一次元ルベーグ測度の積(b−a)(d−c)に等しい。
ある種の面積概念の拡張で、②の考え方が、やはり「閉区間[a,b]の外側での事象発生率は0」と置く連続一様分布の定義と重なってきます。そしてかかる連続一様分布、実はベータ関数B(α,β)と密接な関係を有するβ分布(第一種ベータ分布)の以下の形での特殊例に過ぎないのです。
Wikipedia「ベータ関数」
Wikipedia「ベータ分布」
第一種ベータ分布f(x;α,β)=\frac{x^{α-1}(1-x)^{β-1}}{B(α,β)}
- B(α,β)はベータ関数、確率変数xの取る値は0≤x≤1、パラメータα,βはともに正の実数。ここでパラメーターα=β=1と置くと、ベータ関数はベータ分布の確率密度関数が積分して1となる定数項として導入されたものなのでB(1,1)=1となって区間[0,1]で連続一様分布と重なる。
確率密度関数f(x)=\frac{x^{1-1}(1-x)^{1-1}}{B(1,1)}=\frac{x^0(1-x)^0}{1}=1
- なお、この場合のベータ分布の期待値について調べると
\frac{α}{α+β}=\frac{θ}{1+1}=\frac{θ}{2}
- 分散について調べると
\frac{αβ}{(α+β)^2(α+β+1)}=\frac{θ^2}{(1+1)^2(1+1+1)}=\frac{θ^2}{4*3}=\frac{θ^2}{12}
そのまま連続一様分布の期待値$\frac{a+b}{2}$や分散$\frac{(b-a)^2}{12}$に対応しないのがもどかしいところ。詳しい考え方は分かりませんが、もしかしたらここ仮設定した変数θの制約a+b=b-aを満たすにはa=0と置かないといけないジレンマが、ベータ分布との対応が区間[0,1]に限られる理由なのかもしれません。
連続一様分布の累積分布関数
ここまで確率密度関数(PDF=Probability Density Function、)について目を向けてきました。
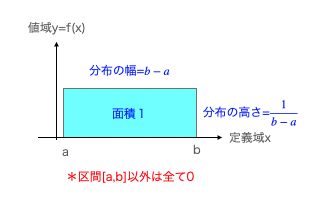
f(x)=
\left\{
\begin{array}{ll}
0 & (x<a) \\
\frac{1}{b-a} & (a≦x≦b) \\
0 & (x>b)
\end{array}
\right.
ここでは、それを積分した結果得られる累積分布関数(CDF=Cumulative Distribution Function)に目を向けたいと思います。
統計Web「15-3. 連続一様分布1」
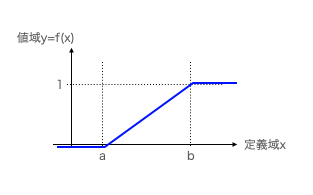
f(x)=
\left\{
\begin{array}{ll}
0 & (x<a) \\
\frac{x-a}{b-a} & (a≦x≦b) \\
1 & (x>b)
\end{array}
\right.
- x<aの場合…-∞≦X<xの範囲でf(t)=0となるのでf(x)=0。
f(x)=P(-∞≦X≦x)=\int_{-∞}^xf(t)dt=\left[0\right]_{-∞}^x=0
- a≦x<bの場合…求める範囲は-∞≦X<xだが、-∞≦x<aの範囲でf(x)=0となるのでa≦x≦xの範囲のみを考える。
f(x)=P(-∞≦X≦x)=P(a≦X≦b)=\int_a^xf(t)dt=\int_a^x\frac{1}{b-a}dt
=\left[\frac{1}{b-a}\right]_a^x=\frac{x-a}{b-a}
- x>bの場合…f(t)=0なのでf(x)=0。従ってa≦x≦bの区間についてのみ考える。
f(x)=P(-∞≦X≦x)=P(a≦X≦b)=\int_a^bf(t)dt=\int_a^b\frac{1}{b-a}dt
=\left[\frac{1}{b-a}\right]_a^b=\frac{b-a}{b-a}=1
「定積分とは何か」なる定義に迫る最も根本的な例題ともなってる訳ですね。ただしここで見掛け上(座標軸上)評価軸ax+bに沿って見える分布が「 「ガウスの誤差関数」成立時点における分散概念の意味」単元で検討した様に「外れ値の混入によって見掛け上分散幅が広がっているだけの水平評価軸$x≒\bar{X}$や垂直評価軸$y≒\bar{Y}$に沿った分布」である可能性を無闇に切り捨てる事は出来ません。そこに(ガウスの時代にはなかった)近代統計学特有のジレンマが存在する訳です。
連続一様分布の最尤量
この単元はほとんど以下の記事の引き写しとなります。
あつまれ統計の森「一様分布の不偏推定量・最尤推定量とその直感的な解釈」
連続一様分布とその確率密度関数と累積分布関数の再定義
①一様分布のU[0,θ]の確率密度関数f(x|θ)を下記のように考える。
f(x|θ)=
\left\{
\begin{array}{ll}
0 & (x<0) \\
\frac{1}{θ} & (0≦x≦θ) \\
0 & (x>θ)
\end{array}
\right.
上記において、θ>0は前提としたが、定義の話であるので単に「そのように定めた」と解釈すればよく、一般性は失われない。
②一様分布の累積分布関数をF(x)とすると、F(x)は下記のように表される。
f(x|θ)=
\left\{
\begin{array}{ll}
0 & (x<0) \\
\int_0^x\frac{1}{θ}dX & (0≦x≦θ) \\
0 & (x>θ)
\end{array}
\right.
③上記において$F(x)=\int_0^x\frac{1}{θ}dX$は下記のように計算される。
F(x)=\int_0^x\frac{1}{θ}dX=\left[\frac{1}{θ}\right]_0^x=\frac{x-0}{θ}=\frac{x}{θ}
確かにこの様に単純化して考えると随分と取り回しが良くなりますね。
標本からの一様分布の推定
母集団と標本を考えるとき、標本から母集団のパラメータを求めることを推定という。ここでは一様分布U[0,θ]に沿って、標本$X=(X_1,X_2,…,X_n)$が得られたと考える。
上記のように標本が得られた際に、母集団のパラメータθをどのように考えれば良いかを考えるときに、標本が複数であることを鑑みて標本の最大値に着目することがまず考えられる。たとえば標本$X=(X_1=3,X_2=2,X_3=6)$が得られたとき、Θの値を考えるにあたっては$X_3=6$に着目するのが良いと思われる。が、$\hat{θ}=6$のようにθを導出して良いかについては難しいところで、標本が母集団から小さな値が偶然に観測されたと考えることもできる。
そう考えると、「単に最大値に着目すること自体は理にかなっている一方で、そのまま最大値を用いて良いかについては議論の余地がある」というのが客観的な見解であると思われる。標本が多い場合は最大値に近い値がθである傾向が比較的大きく、標本が少ない場合はその限りでないかもしれない。
ここで尤度(likelihood)概念の原義に立ち返って考えてみましょう。
Wikipedia「尤度関数」
B = b であることが確定している場合に、 A が起きる確率(条件付き確率)をP(A|B=b)とする。このとき、逆に A が観察で確認されていることを基にして、上記の条件付き確率を変数bの関数として尤度関数(Likelihood Function)という。また一般には、それに比例する関数からなる同値類L(A|b)=αP(A|B=b)をも尤度関数という(ここでαは任意の正の比例定数)。
Wikipedia「条件付き確率(Conditional Probability)」
Wikipedia「同値類(Equivalence Class)」
具体例として挙げられているのは以下。
コインを投げるときに、表が出る('H')確率が$p_H$であれば、2回の試行で2回とも表が出る('HH')確率は$p_H^2$である。従って$p_H$=0.5ならば2回とも表が出る確率は0.25となる。このことを次のように示す:
$P(HH|P_H=0.5)=0.25$
これのもう1つの言い方として、「観察結果が'HH'ならば$p_H$=0.5の尤度は0.25である」、つまり
$L(P_H=0.5|HH)=P(HH|P_H=0.5)=0.25$
と言える。一般には
$L(P_H=x|HH)=P(HH|P_H=x)=x^2$
と書ける。 しかしこれを、「観察値が0.25ならば、1回投げて表の出る確率は pH = 0.5」という意味にとってはならない。
①極端な場合を例にとるなら「観察結果が'HH'ならば pH = 1 の尤度は1」ともいえるが、明らかに、観察値が1だからといって表の出る確率$p_H$=1ということはない。'HH'という事象は$p_H$の値が0より大きく1以下のいくつであっても起こり得るからである。
②$L(P_H=x|HH)$の値はxが1に近づくほど大きくなる(しかし現実にはpH はおよそ0.5である場合が多い)が、観察はたった2回の試行に基づくもので、それからとりあえず「$p_H$=1が尤もらしい」といっているにすぎない。
また尤度関数は確率密度関数ではなく、積分しても一般に1にはならない。上の例では$p_H$に関する[0, 1]区間の尤度関数の積分は$\frac{1}{3}$で、これからも尤度密度関数を$p_H$に対する確率密度関数としては解釈できないことがわかる。
要するに尤度に関する話題はすぐに「正規分布のパラメーターたる平均と分散の最適化問題」に帰着する傾向が見られますが…
【統計学】尤度って何?をグラフィカルに説明してみる。
一様分布の尤度については、例えば離散一様分布における「出目の総数が不明のサイコロ」の様に考えないといけないという事です。
- とりあえず、それまで出た最大の出目を最尤値θと想定し、それぞれの出目の出現確率を均等に$\frac{1}{θ}$と考える。
- もし違う情報が入ってきたら(例えばそれまでの最大値θを超える出目が出たり、出目の出現確率に優位な偏りが見出された場合には)その都度、最尤値θを更新する。
人間が考える「戦略」は大体こんな感じですが、これを数理的に表現すると…
あつまれ統計の森「一様分布の不偏推定量・最尤推定量とその直感的な解釈」
- 最尤法の考え方(Likelihood)を用いて計算した推定量$\hat{θ}_l$
\hat{θ}_l=max(X_1,X_2,…,X_n)
- 不偏推定量の考え方(Unbiased)を用いて計算した推定量$\hat{θ}_{ub}$
\hat{θ}_{ub}=(1+\frac{1}{n})max(X_1,X_2,…,X_n)(n=標本数)
上記を確認すると「最尤推定量」は標本の最大値をそのまま用いており、「不偏推定量」は標本の最大値に補正をかけていることがわかる。「最尤推定量」と「不偏推定量」はどちらもn→$\tilde{∞}$のような標本の大きな際は同じ結果となる一方で、標本数が少ない場合は「最尤推定量」よりも「不偏推定量」の方が妥当な結果が得られるであろうことは推測できる。
ここで注意しておくと良いのが一様分布の例では「不偏推定量」の結果の方が良いように見えるが、これは「不偏推定量が最尤推定量よりも良い」という結論を導出するものではないことである。どちらの推定量も万能ではないので、それぞれ大まかな考え方を抑えつつ、活用していくのが良いと思われる。
未知の領域についての話題については、誰もがこの様に慎重にならねばならないという見本の様な文章ですね。
最尤法を用いたパラメータ推定
以下はもう完全に引用となってしまいます。
あつまれ統計の森「一様分布の不偏推定量・最尤推定量とその直感的な解釈」
標本$X=(X_1,X_2,…,X_n)$に関する同時確率密度関数は下記のように表される。
KIT数学ナビゲーション「同時確率分布」
F(X_1,X_2,…,X_n|θ)=\frac{1}{θ^n}(0≦X_1,X_2,…,X_n≦θ)
上記において$\frac{1}{θ^n}$はθに関する単調減少関数であり、θの値が大きくなればなるほど$\frac{1}{θ^n}$の値は小さくなる。最尤推定量は「同時確率密度関数=尤度」を最大にするパラメータの値を求める手法であるので、θの値はなるべく小さな値が良いという結論になる。一方でここで注意が必要なのが、「θは観測された標本のどの値よりも小さくなってはならない」という制約が存在することである。
よって、「θは観測された標本のどの値よりも小さくなってはならない」かつ「単調減少関数$\frac{1}{θ^n}$よりθの値はなるべく小さな値が良い」を勘案し、Θを標本の最大値で推定を行おうというのが最尤法を用いた一様分布のパラメータ推定である。
\hat{θ}_l=max(X_1,X_2,…,X_n)
数式で表すと上記のように表すことができる。正規分布やベルヌーイ分布などの最尤推定とは異なり、一様分布の最尤推定は「パラメータで微分した関数=0」を解くわけではないことに注意が必要である。
不偏推定量を用いた推定量
\hat{θ}_{ub}=(1+\frac{1}{n})max(X_1,X_2,…,X_n)(n=標本数)
この計算が最適量として算出される過程の記述に全くついていけませんでした。
あつまれ統計の森「一様分布の不偏推定量・最尤推定量とその直感的な解釈」
- ここに登場する「統計的決定理論における十分統計量」なる概念がまず分からない。
コトバンク「統計的決定理論(Statistical Decision Theory)」
*記述によれば「十分統計量」とは「標本$X=(X_1,X_2,…,X_n)$について知らなくても、十分統計量$T(X)=T(X_1,X_2,…,X_n)$を知れば、未知のパラメータθの推定には十分である統計量」との事(今なんて?)。
これからの課題とします。
ルベール測度論との関係
明かに連続一様分布の区画(a,b)概念はルベール測度(Lebesgue measure)b-a概念と関わってきます。
Wikipedia「ルベール測度」
- ただし外測度(Outer Measure)を常に0と置いてる時点で相応の単純化がなされているとも?
Wikipedia「外測度」 - どうやらこの辺りの考え方は「最外縁の補集合を空集合φ=0と考える」集合論上の「閉世界仮説(Closed World Assumption)」と密接に関係してくる様だ?
ベン図と組み合わせ計算と確率演算
ここで各区画の正規分布との対応を見てみましょう。
【Token】「何も起こってない」ディフォルト状態としての正規分布
- 0から+1の区画(ルベール測度b-a=1-0=1、正規分布でいう平均$\frac{1}{2}$,分散2)において、連続一様分布の確率密度関数$f(x)=\frac{1}{1-0}=1$の期待値(平均)は$\frac{1-0}{2}=\frac{1}{2}$,分散は$\frac{(1-0)^2}{12}=\frac{1}{12}$
- -1から+1の区画で(ルベール測度b-a=1-(-1)=2、正規分布でいう平均0,分散1)において、連続一様分布の確率密度関数$f(x)=\frac{1}{1-(-1)}=\frac{1}{2}$の期待値(平均)は$\frac{1-1}{2}=\frac{0}{2}=0$、分散は$\frac{(1-(-1))^2}{12}=\frac{2^2}{3*2^2}=\frac{1}{3}$
- 0から+2の区画で(ルベール測度b-a=2-0=2、正規分布でいう平均1,分散1)において、連続一様分布の確率密度関数$f(x)=\frac{1}{2-0}=\frac{1}{2}$の期待値(平均)は$\frac{2-0}{2}=\frac{2}{2}=1$、分散は$\frac{(2-0)^2}{12}=\frac{2^2}{3*2^2}=\frac{1}{3}$
区画(0,1)の特殊性が浮かび上がってきますね。ここではさらに$a=0,b=x_{max}$と置いてその確率密度関数(PDF=Probability Density Function)と累積分布関数(CDF=Cumulative Distribution Function,)の微積分計算過程を眺めていきましょう。

- 区画$(0,x_{max})$における連続一様分布の確率密度関数$f(x)=\frac{1}{x_{max}-0}=\frac{1}{x_{max}}$をxで積分して獲られる累積分布関数F(x)
F(x)=
\left\{
\begin{array}{ll}
0 & (x<0) \\
\frac{x-0}{x_{max}-0}=\frac{x}{x_{max}} & (0≦x≦x_{max}) \\
1 & (x>x_{max})
\end{array}
\right.
- 上掲の累積分布関数F(x)の水平軸と垂直軸を逆転させた(すなわち区画(0,1)における0から$x_{max}$への変遷を観察対象とする)x=F(y)関数への置換。
F(x)=
\left\{
\begin{array}{ll}
0 & (\frac{x}{x_{max}}<0) \\
x & (0≦\frac{x}{x_{max}}≦1) \\
x_{max} & (1>\frac{x}{x_{max}})
\end{array}
\right.
- 上掲のx=F(y)関数を区画(0,1)における累積分布関数F(x)=xと置き、これをxで微分する形で得られる確率密度関数f(x)=1。これが上掲の「ベータ分布B(a,b)においてa=b=1となる場合」に対応する。
f(x)=
\left\{
\begin{array}{ll}
0 & (x<0) \\
1 & (0≦x≦1) \\
0 & (1>x)
\end{array}
\right.
①以下の投稿で言及した「質量1、加速度1と単純化した場合のニュートンの運動三法則」を連想察せます。力F=加速度a=「傾き1」となって慣性の法則「外力が作用しない限り、物体は静止状態または等速直線運動を続ける」だけが残る印象。
【Token】物理学と数学の接点②ニュートンの運動3法則
②そして、こうした「区画(0,1)における確率密度間数f(x)=1(つまりベータ関数B(a,b)でa=b=1となる場合)」過程そのものが以下の投稿で言及した「最小二乗法における傾きの抽出過程」と重なってくるのです。
【Token】相関係数と線形回帰
なんとこうした考え方は全て「ラドンニコディム微分」の入口に過ぎなかった?
ルベーグの微分定理とその証明~測度の微分を添えて~
そんな感じで以下続報…