はじめに
以下の書籍を参考にしながら,統計の基礎を学び直した軌跡の,準備〜データ編です.
書籍を参考にしながら勝手に解釈してまとめたり,省略したり補足したりしていますので,書籍に沿って進めたい方は購入をオススメします!界隈で有名な一冊ですし,統計指標のビジュアライズが秀逸で理解を助けてくれます.
この記事は5部構成の1つ目です.以下も参照ください.
動機
問題にぶつかったときに都度ピンポイントで調べたり勉強して誤魔化してきたものの,特に統計や確率の基礎知識が凸凹していてはいけない!と思い立ちました.
勉強したい分野は他にも沢山ありますが,統計・確率は機械学習などに限らず,あらゆる分野で使われているし,知っておいて損は無いランキング上位に位置している分野だと勝手に思っています.
注意点
今回の記事では,あくまで統計の基礎にフォーカスしています.機械学習やデータ分析を実装するためのプログラミングがメインではないため,ライブラリやサービスの説明/コメントは最小限に留めています.ただし,今回フォーカスした領域について,エンジニアという立場から,なるべくコードを交えて解りやすく説明することは意識しています.分かりにくいところなどがあればコメントください.随時修正・加筆していきます!
使用している技術
- Python - プログラミング言語
- NumPy - 数値計算ライブラリ
- SciPy - 科学計算ライブラリ
- pandas - データ解析ライブラリ
- matplotlib - グラフ描画ライブラリ
- seaborn - グラフ描画ライブラリ
- Colaboratory - ↑をブラウザ上で手軽に実行できるサービス
これらについて軽く触ったことがあれば理解出来る内容になっているはず.特にColabはアクセスするだけで無料ですぐに動かせます!seabornは書籍では使われていませんが,ケースによってはmatplotlibより簡単にグラフ描画できることがあったため,使用しています.
-
今回の記事のサンプルコード
- 書籍のコードとは異なる部分が多いです
-
書籍のサンプルコード
- Pythonやライブラリのチュートリアルなども充実しています!
構成
書籍のタイトルにある統計解析とは,以下によると,
大量のデータを収集・探索・分析し、その結果を提示することを通じて、データに含まれるパターンや傾向を明らかにする
とのこと.これができるスキルを身に付けるため,以下の3つに関する技術をPythonによるプログラミングを通じて順番に学んでいきます.
- データ・・・この記事
- 確率
- 推測
ここで,これら3つのワードを使って引用文を言い換えると,「確率的に得られたデータから,観測対象の特性を推測すること」が,統計解析です.統計解析に確率の知識が必要になってくる理由は,得られるデータが観測対象のほんの一部であることがほとんどだからです.
準備
Colaboratory
Colaboratoryを使用すればPythonや各種ライブラリをそのまま実行できるので,準備はシンプルです.ただしGoogleアカウントの登録は必須.
まずGoogleドライブにアクセスし,適当なディレクトリで右クリック
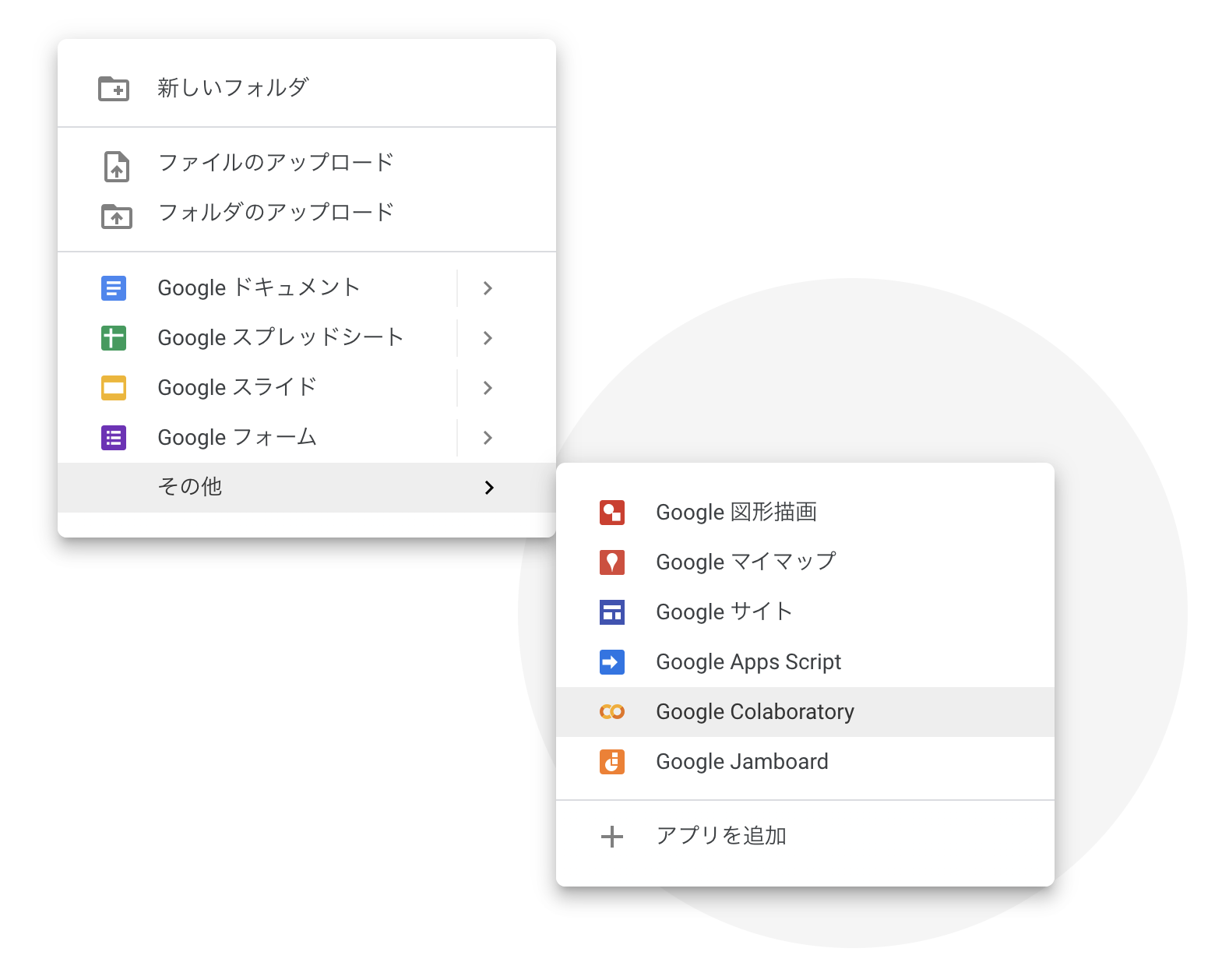
その他 → Google Colaboratoryを選択
Colaboratory へようこそを参考にテキストやコードを書いて実行
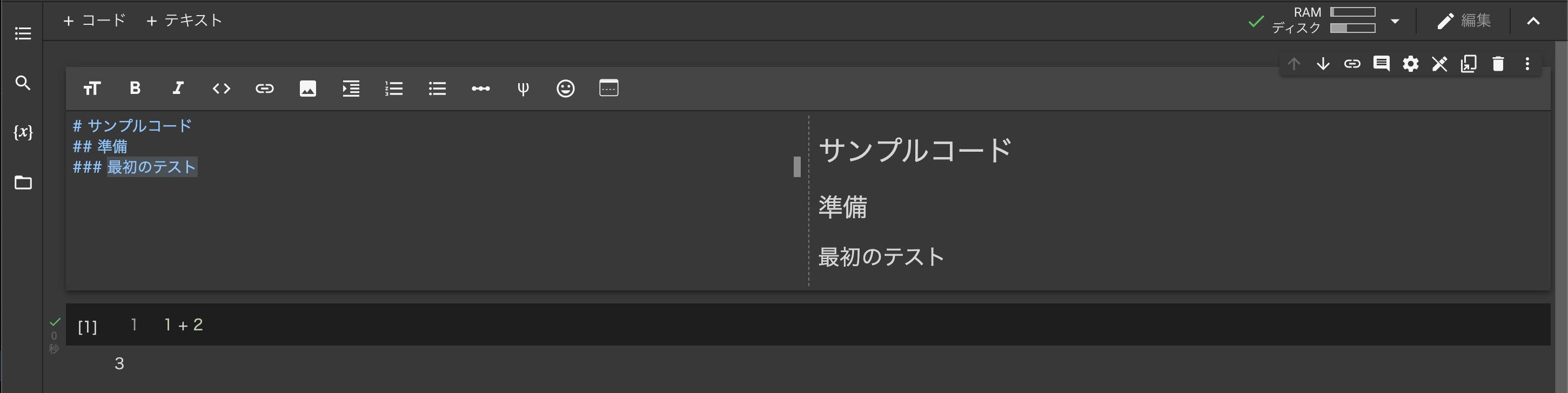
Colabでは,最後の行のコードの実行結果が,print不要でそのまま出力表示されます.
使用するデータ
書籍で使用しているデータはgithub上で公開されています.Colab上でgit cloneして配置します.今回はpython_stat_sample/dataディレクトリをColabのデフォルトでディレクトリである/content配下に配置します.
コマンドの頭に!を付加すると,以下のようなコマンドもColab上で実行することができます.
!git clone https://github.com/ghmagazine/python_stat_sample.git
Cloning into 'python_stat_sample'...
remote: Enumerating objects: 130, done.
remote: Total 130 (delta 0), reused 0 (delta 0), pack-reused 130
Receiving objects: 100% (130/130), 8.22 MiB | 12.64 MiB/s, done.
Resolving deltas: 100% (59/59), done.
!mv ./python_stat_sample/data ./data
!ls ./data
ch10_access.csv ch11_potato.csv ch12_scores_reg.csv ch3_anscombe.npy
ch10_enquete.csv ch11_training_ind.csv ch1_sport_test.csv ch4_scores400.csv
ch11_ad.csv ch11_training_rel.csv ch2_scores_em.csv
最後に,matplotlibで日本語を表示しようとすると文字化けしてしまうため,日本語化対応のライブラリをインストールしておきます.
!pip install japanize-matplotlib
Looking in indexes: https://pypi.org/simple, https://us-python.pkg.dev/colab-wheels/public/simple/
Collecting japanize-matplotlib
Downloading japanize-matplotlib-1.1.3.tar.gz (4.1 MB)
|████████████████████████████████| 4.1 MB 8.9 MB/s
Requirement already satisfied: matplotlib in /usr/local/lib/python3.7/dist-packages (from japanize-matplotlib) (3.2.2)
Requirement already satisfied: numpy>=1.11 in /usr/local/lib/python3.7/dist-packages (from matplotlib->japanize-matplotlib) (1.21.6)
Requirement already satisfied: kiwisolver>=1.0.1 in /usr/local/lib/python3.7/dist-packages (from matplotlib->japanize-matplotlib) (1.4.3)
Requirement already satisfied: python-dateutil>=2.1 in /usr/local/lib/python3.7/dist-packages (from matplotlib->japanize-matplotlib) (2.8.2)
Requirement already satisfied: pyparsing!=2.0.4,!=2.1.2,!=2.1.6,>=2.0.1 in /usr/local/lib/python3.7/dist-packages (from matplotlib->japanize-matplotlib) (3.0.9)
Requirement already satisfied: cycler>=0.10 in /usr/local/lib/python3.7/dist-packages (from matplotlib->japanize-matplotlib) (0.11.0)
Requirement already satisfied: typing-extensions in /usr/local/lib/python3.7/dist-packages (from kiwisolver>=1.0.1->matplotlib->japanize-matplotlib) (4.1.1)
Requirement already satisfied: six>=1.5 in /usr/local/lib/python3.7/dist-packages (from python-dateutil>=2.1->matplotlib->japanize-matplotlib) (1.15.0)
Building wheels for collected packages: japanize-matplotlib
Building wheel for japanize-matplotlib (setup.py) ... done
Created wheel for japanize-matplotlib: filename=japanize_matplotlib-1.1.3-py3-none-any.whl size=4120275 sha256=58635acca06dee9bc3ad73aa947b7f55d8ffea99e9cf5b35977b33a06123b0ef
Stored in directory: /root/.cache/pip/wheels/83/97/6b/e9e0cde099cc40f972b8dd23367308f7705ae06cd6d4714658
Successfully built japanize-matplotlib
Installing collected packages: japanize-matplotlib
Successfully installed japanize-matplotlib-1.1.3
これで準備が整いました.
早速,内容に入っていきましょう!
データの種類
データの種類には様々な種類がありますが,書籍で扱われているのはテーブルデータ(構造化データ)ですので,こちらに絞ってデータの種類を見ていきます.
表(DataFrame)
Pandasを使用してcsvファイルをDataFrameとして読み込みます.
import pandas as pd
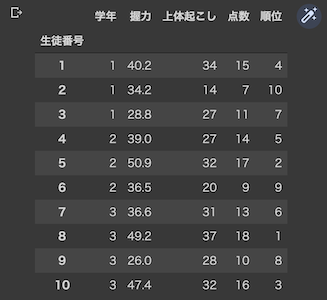
df = pd.read_csv('data/ch1_sport_test.csv', index_col='生徒番号')
df
PandasのDataFrameは表形式で表示されます.コードの途中で表を表示したいときはdisplay(df)とすればOK.右上のペンがキラキラしたようなアイコンを押すと,フィルタリングや並び替えが可能な表形式に切り替えることができます.便利ですね!
使い方はこちらを参照.ここからMarkdownに変換してQiitaに貼り付けることができたので,以降はこの機能を使っていきます.
| 生徒番号 | 学年 | 握力 | 上体起こし | 点数 | 順位 |
|---|---|---|---|---|---|
| 1 | 1 | 40.2 | 34 | 15 | 4 |
| 2 | 1 | 34.2 | 14 | 7 | 10 |
| 3 | 1 | 28.8 | 27 | 11 | 7 |
| 4 | 2 | 39.0 | 27 | 14 | 5 |
| 5 | 2 | 50.9 | 32 | 17 | 2 |
| 6 | 2 | 36.5 | 20 | 9 | 9 |
| 7 | 3 | 36.6 | 31 | 13 | 6 |
| 8 | 3 | 49.2 | 37 | 18 | 1 |
| 9 | 3 | 26.0 | 28 | 10 | 8 |
| 10 | 3 | 47.4 | 32 | 16 | 3 |
列(Series)
DataFrameは生徒番号や学年など列データの集まりです.
df['点数']
生徒番号
1 15
2 7
3 11
4 14
5 17
6 9
7 13
8 18
9 10
10 16
Name: 点数, dtype: int64
実行結果が少し分かりにくいのですが,indexに生徒番号を設定しているため,左側に生徒番号が,右側に点数のデータが表示されています.エンジニアに親しみのある1次元配列で表現すると分かりやすいかもしれません,,,
df['点数'].values
array([15, 7, 11, 14, 17, 9, 13, 18, 10, 16])
実体としては一次元配列として保持されているようです.
ここでこの1次元のデータのことを,統計やデータ分析の分野では変数や特徴などと呼びます.Webエンジニアからすると変数はもっと広い意味を持っているイメージで,個人的には最初違和感を感じてしまいました.そこは,
1次元配列のデータを界隈では「変数」と表現する
と何処かに書いてあるルールとして認識するしかないと思っています.
変数の分類
変数は以下のように大きく2つに分類して扱うことが多いです.
- 質的変数・・・性別や血液型など,種類を区別する(カテゴリ変数とも)
- 量的変数・・・身長やアクセス数など,量を表現する
また尺度水準によって更に細かく分類できます.
- 名義尺度・・・順序や大小がなく単に区別するだけ
- 順序尺度・・・順序や大小があるが,比較ができず差にも意味が無い
- 間隔尺度・・・順序や大小に加えて,差に意味があるが,比に意味が無い
- 比例尺度・・・順序,大小,差,比すべてに意味がある
書籍では名義・順序は質的変数,間隔・比例は量的変数に分類しています.しかし質的変数・量的変数は,「分類」というより変数を「どう扱うか」によって変わってくる感覚があります.順序尺度に当てはまる変数を,量的変数として扱おうと思えば扱うことができます.あくまで実践的な感覚であって理論的には間違っているのかもしれませんが..
更に別の切り口での分類.これは明快ですね.
- 離散型・・・とびとびの値
- 連続型・・・切れ目が無い連続した値
これらの分類情報を基に,読み込んだデータの種類を表にしてみました.
| 変数名 | 変数 | 尺度 | 型 |
|---|---|---|---|
| 生徒番号 | 質的 | 名義 | 離散 |
| 学年 | 量的 | 間隔 | 離散 |
| 握力 | 量的 | 比例 | 連続 |
| 状態起こし | 量的 | 比例 | 離散 |
| 点数 | 量的 | 比例 | 連続? |
| 順位 | 質的 | 順序 | 離散 |
点数について今回は連続型としていますが,例えば80.5点みたいな点数が存在しないケースでは,厳密には連続型とは言えないんじゃないか?だったり,仮に10点満点のテストだったら明らかに離散しているので,ケースバイケースで変わってくるような気がします.
1次元データ
次に,変数(1次元データ)の特徴を把握するために,様々な指標を用いてデータを整理する方法について記載します.1次元データは変数と記載したにも関わらず,以降もデータというワードを多用しています..わかり易さを重視していると信じて,呼称はなるべく書籍に寄せることにします.
結果表示を見やすくするため,表示設定を行っておきます.
import numpy as np
import pandas as pd
%precision 3
pd.set_option('precision', 3)
使用するデータを読み込みます.
df = pd.read_csv('data/ch2_scores_em.csv', index_col='生徒番号')
df.info()
Int64Index: 50 entries, 1 to 50
Data columns (total 2 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 英語 50 non-null int64
1 数学 50 non-null int64
dtypes: int64(2)
memory usage: 1.2 KB
英語の数学のテスト結果が50件,というデータです.最初の5件を表示してみます.
df.head()
| 生徒番号 | 英語 | 数学 |
|---|---|---|
| 1 | 42 | 65 |
| 2 | 69 | 80 |
| 3 | 56 | 63 |
| 4 | 41 | 63 |
| 5 | 57 | 76 |
中心の指標(代表値)
ここから,データを要約する1つの値を求めるいくつかの指標について説明します.先程読み込んだデータから英語の点数10人分を抽出して使用することにします.
data = np.array(df['英語'][:10])
index = pd.Index(list('ABCDEFGHIJ'), name='生徒')
scores_df = pd.DataFrame({'点数': data}, index=index)
scores_df
| 生徒 | 点数 |
|---|---|
| A | 42 |
| B | 69 |
| C | 56 |
| D | 41 |
| E | 57 |
| F | 48 |
| G | 65 |
| H | 49 |
| I | 65 |
| J | 58 |
平均値(Mean/Average)
みんなが知っている全部の点数を足して件数で割ったものです.
np.mean(scores_df)
点数 55.0
dtype: float64
中央値(Median)
データの大きさを順番に並べたとき,ちょうど中央に位置をする値です.大きな外れ値に平均値が引っ張られてしまうのに対し,中央値はその影響を受けにくいという特徴があります.
np.median(scores_df)
56.500
今回のケースではデータが10件で偶数なので,中央に位置する値が2つあります.その場合,2つの値の平均値が中央値として抽出されます.
最頻値(Mode)
データの中で最も多く出現する値です.値のバリエーションが少ない質的変数でよく使われる指標なので,サンプルデータはこの場で作成します.
pd.Series([0, 1, 1, 2, 3, 3, 3, 4]).mode()
0 3
dtype: int64
少し分かりにくいですが,3が最頻値です.NumPyでは直接最頻値を求める関数が無かったため,pandasのSeriesの関数を用いています.
ばらつきの指標
平均値だけを用いてデータを分析するケースはよく目にしますが,データのばらつき(分布)を確認すれば,データをより詳細に分析できます.
偏差(Deviation)
1つの値が平均値からどれだけ離れているか,を表す指標です.
mean = np.mean(scores_df['点数'])
scores_df['偏差'] = scores_df['点数'] - mean
scores_df
| 生徒 | 点数 | 偏差 |
|---|---|---|
| A | 42 | -13.0 |
| B | 69 | 14.0 |
| C | 56 | 1.0 |
| D | 41 | -14.0 |
| E | 57 | 2.0 |
| F | 48 | -7.0 |
| G | 65 | 10.0 |
| H | 49 | -6.0 |
| I | 65 | 10.0 |
| J | 58 | 3.0 |
その値が平均と比べてどの程度ばらついているか,値毎に確認することができます.
分散(Variance)
しかし,データ全体のばらつきを確認するために偏差を平均してみると,,,
np.mean(scores_df['偏差'])
0.000
となってしまいます..平均との差は,負の値と正の値の合計が同じになるからです.そこで,偏差を2乗した平均を考えます.これが分散です.
scores_df['偏差二乗'] = scores_df['偏差'] ** 2
np.mean(scores_df['偏差二乗'])
86.000
NumPyのvarを使って点数から直接算出することができます.
np.var(scores_df['点数'])
86.000
分散について注意点を2つ挙げておきます.
- pandasの分散はデフォルト設定が不偏分散になっているため計算結果が異なる
-
Series.var関数の引数ddof=0とすれば標本分散になる - 詳細は書籍を参照
-
- なぜ分散が絶対値の平均ではなく2乗の平均なのかは,色々と都合が良いかららしい,,,
- 詳細は以下を参照
標準偏差(Standard Deviation)
ここで,改めてデータを確認します.
scores_df
| 生徒 | 点数 | 偏差 | 偏差二乗 |
|---|---|---|---|
| A | 42 | -13.0 | 169.0 |
| B | 69 | 14.0 | 196.0 |
| C | 56 | 1.0 | 1.0 |
| D | 41 | -14.0 | 196.0 |
| E | 57 | 2.0 | 4.0 |
| F | 48 | -7.0 | 49.0 |
| G | 65 | 10.0 | 100.0 |
| H | 49 | -6.0 | 36.0 |
| I | 65 | 10.0 | 100.0 |
| J | 58 | 3.0 | 9.0 |
scores_df.mean()
点数 55.0
偏差 0.0
偏差二乗 86.0
dtype: float64
偏差二乗の平均が分散になるので,86.0が点数の分散です.偏差を2乗しているため,点数と同じスケールでデータのばらつきを表現することができていません..偏差は13.0とか-7.0なのに対して,偏差二乗は100を超える数字が目立ちます.
そこで,分散をルートすることで求められる標準偏差という指標が使われます.2乗した値をルートで囲って元のスケールに戻したということです.
np.sqrt(np.var(scores_df['点数']))
9.274
NumPyのstdを使えば一気に計算できます.pandas使用時の注意点は分散のときと同じです.
np.std(scores_df['点数'])
9.274
点数と同じスケールでばらつきを表現できていますね!
最小値/最大値(Min/Max)
これはそのまま,データの最小値と最大値です.
scores_df['点数'].max(), scores_df['点数'].min()
(69, 41)
分位数(Quantile/Percentile)
データの中央に位置する値が中央値でしたが,最小値を0.0,最大値を1.0としたとき,その間の割合に位置する値が,分位数です.外れ値の影響で,最小値や最大値ではデータの特性を上手く表せない,というようなケースで有用です.
quantileで求めるときは0.0〜1.0を,percentileではパーセンテージ0〜100を指定します.どちらも実行結果は同じ.ちなみに0.5を指定すると中央値と同じ値になります.
np.quantile(scores_df['点数'], 0.25), np.quantile(scores_df['点数'], 0.75)
np.percentile(scores_df['点数'], 25), np.percentile(scores_df['点数'], 75)
(48.250, 63.250)
特に,以下の分位数をまとめて四分位数と呼びます.
- 25%・・・第一四分位数
- 50%・・・第二四分位数(中央値)
- 75%・・・第三四分位数
また,書籍には出てきませんでしたが,これまで挙げてきた以下5つをまとめて5数要約と呼びます.
- 最小値
- 第一四分位数
- 中央値
- 第三四分位数
- 最大値
文字通り,データを要約する5つの数ということですね.これらは後に説明する四分位範囲や,箱ひげ図に用いられています!
範囲(Range)
最大値と最小値の範囲を求めて,データのばらつきを表現します.
scores_df['点数'].max() - scores_df['点数'].min()
28
標準偏差と比較したときの違いは以下
- 標準偏差は平均値との差が基になっているため,範囲の半分以下になる
- 範囲は平均値ではなく最大値
- 外れ値の影響を大きく受ける
四分位範囲(IQR)
先ほど説明した分位数を用いて範囲を算出します.最大値と最小値を用いた範囲と比べて外れ値の影響が小さい指標です.
np.quantile(scores_df['点数'], 0.75) - np.quantile(scores_df['点数'], 0.25)
15.000
quantileの引数として指定している割合を調整することで,ばらつき範囲を調整することができます.
正規化(Normalization)
平均や分散に依存せずに,データの相対的な位置関係が分かるように変換することが,正規化です.
例えば,高校や大学受験で用いられる偏差値も,正規化の指標の1つです.テストの平均点が何点であれ,そのテストを受けた全員の中での自分の位置関係を正しく教えてくれます.
標準化(Standardization/Z-score)
偏差を標準偏差で割って求めたものが,標準化されたデータです.
Zスコアや基準化変量などと呼ばれるようです.個人的にはscikit-learnのStandardScalerをよく使っていて,「標準にスケーリングされたデータ」みたいなイメージを持っています.言葉が似ていて混乱しがちですが,あくまで標準化は正規化の1つで,Min-Max法など他にもいくつか正規化の手法があります.
scores_df['Zスコア'] = scores_df['偏差'] / np.std(scores_df['点数'])
scores_df['Zスコア']
生徒
A -1.402
B 1.510
C 0.108
D -1.510
E 0.216
F -0.755
G 1.078
H -0.647
I 1.078
J 0.323
Name: Zスコア, dtype: float64
np.mean(scores_df['Zスコア']), np.std(scores_df['Zスコア'])
(-0.000, 1.000)
平均は0.0,標準偏差は1.0になります.標準化は機械学習で頻繁に用いられていますが,標準化によって失われている情報もある,ということを認識した上で使用すべきかと思います.
例えば,標準化されたデータをいくらこねくり回しても,平均点が55で,分散が86,標準偏差が9.274である,という情報を読み取ることはできませんよね,,,データを標準偏差で割ることで,これらの情報が失われたということです.
偏差値(T-score)
さきほど例に挙げた,平均が50,標準偏差が10になるように正規化したデータです.標準化したデータに10を掛けて50を足せばOK.
scores_df['偏差値'] = 50 + 10 * scores_df['Zスコア']
scores_df[['点数', '偏差値']]
| 生徒 | 点数 | 偏差値 |
|---|---|---|
| A | 42 | 35.982 |
| B | 69 | 65.097 |
| C | 56 | 51.078 |
| D | 41 | 34.903 |
| E | 57 | 52.157 |
| F | 48 | 42.452 |
| G | 65 | 60.783 |
| H | 49 | 43.530 |
| I | 65 | 60.783 |
| J | 58 | 53.235 |
標準化されたデータが,皆さんに馴染みのある偏差値に変換されましたね!
視覚化
次に,1次元データを図表で視覚化して,データの特徴を明らかにする方法に関して記載します.50人分の英語の点数を使用します.
english_scores = df['英語']
english_scores.describe().to_frame()
| 英語 | |
|---|---|
| count | 50.0 |
| mean | 58.38 |
| std | 9.80 |
| min | 37.0 |
| 25% | 54.0 |
| 50% | 57.5 |
| 75% | 65.0 |
| max | 79.0 |
度数分布表(Frequency table)
データの分布を知るために,値の範囲を一定の区間に分割し,データを分類してまとめたものが度数分布表です.分割する区間を階級(Class),階級に属している数を度数(Frequency)と言います.
NumPyのhistogramに使用して度数分布表を作成します.
freq, _ = np.histogram(english_scores, bins=10, range=(0, 100))
freq_class = [f'{i}〜{i + 10}' for i in range(0, 100, 10)]
freq_dist_df = pd.DataFrame({'度数': freq}, index=pd.Index(freq_class, name='階級'))
freq_dist_df
| 階級 | 度数 |
|---|---|
| 0〜10 | 0 |
| 10〜20 | 0 |
| 20〜30 | 0 |
| 30〜40 | 2 |
| 40〜50 | 8 |
| 50〜60 | 16 |
| 60〜70 | 18 |
| 70〜80 | 6 |
| 80〜90 | 0 |
| 90〜100 | 0 |
階級値(Class)
各階級を代表する値で,階級の中央の値が使われます.
class_values = [(i + (i + 10)) // 2 for i in range(0, 100, 10)]
class_values
[5, 15, 25, 35, 45, 55, 65, 75, 85, 95]
相対度数(Relative frequency)
全データに対してその階級が占める割合が相対度数です.
rel_freq = freq / freq.sum()
rel_freq
array([0. , 0. , 0. , 0.04, 0.16, 0.32, 0.36, 0.12, 0. , 0. ])
相対度数を合計すると1.0になります.
累積相対度数(Cumulative relative frequency)
相対度数の累積和です.
cum_rel_freq = np.cumsum(rel_freq)
cum_rel_freq
array([0. , 0. , 0. , 0.04, 0.2 , 0.52, 0.88, 1. , 1. , 1. ])
各指標を表にまとめて表示します.
freq_dist_df['階級値'] = class_values
freq_dist_df['相対度数'] = rel_freq
freq_dist_df['累積相対度数'] = cum_rel_freq
freq_dist_df
| 階級 | 度数 | 階級値 | 相対度数 | 累積相対度数 |
|---|---|---|---|---|
| 0〜10 | 0 | 5 | 0.0 | 0.0 |
| 10〜20 | 0 | 15 | 0.0 | 0.0 |
| 20〜30 | 0 | 25 | 0.0 | 0.0 |
| 30〜40 | 2 | 35 | 0.04 | 0.04 |
| 40〜50 | 8 | 45 | 0.16 | 0.2 |
| 50〜60 | 16 | 55 | 0.32 | 0.52 |
| 60〜70 | 18 | 65 | 0.36 | 0.88 |
| 70〜80 | 6 | 75 | 0.12 | 1.0 |
| 80〜90 | 0 | 85 | 0.0 | 1.0 |
| 90〜100 | 0 | 95 | 0.0 | 1.0 |
pandasのcutやqcutなどで同じようなことを実現していましたが,NumPyでも楽に作ることができるんですね,,,
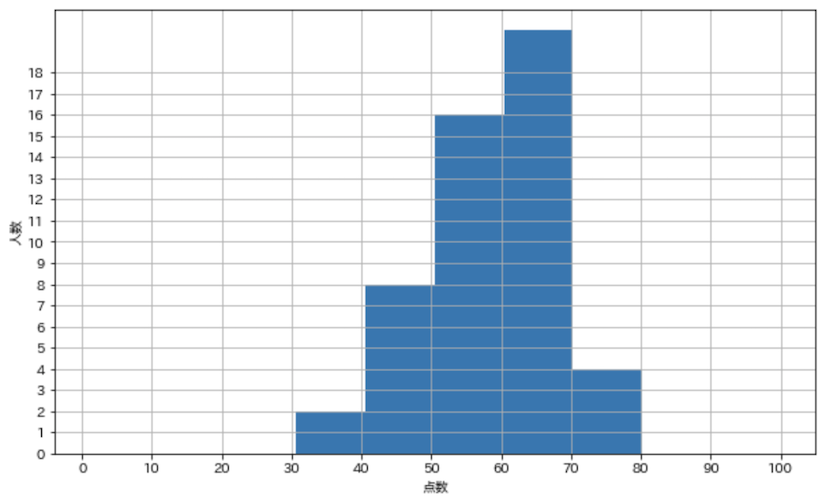
ヒストグラム(Histogram)
作成した度数分布表のデータを基にグラフ描画してみます.
点数の度数分布のグラフ
import matplotlib.pyplot as plt
import japanize_matplotlib
plt.figure(figsize=(10, 6))
plt.hist(english_scores, bins=10, range=(1, 100))
plt.grid(True)
plt.xlabel('点数')
plt.ylabel('人数')
plt.xticks(np.linspace(0, 100, 10 + 1))
plt.yticks(np.arange(0, freq.max() + 1))
plt.show()
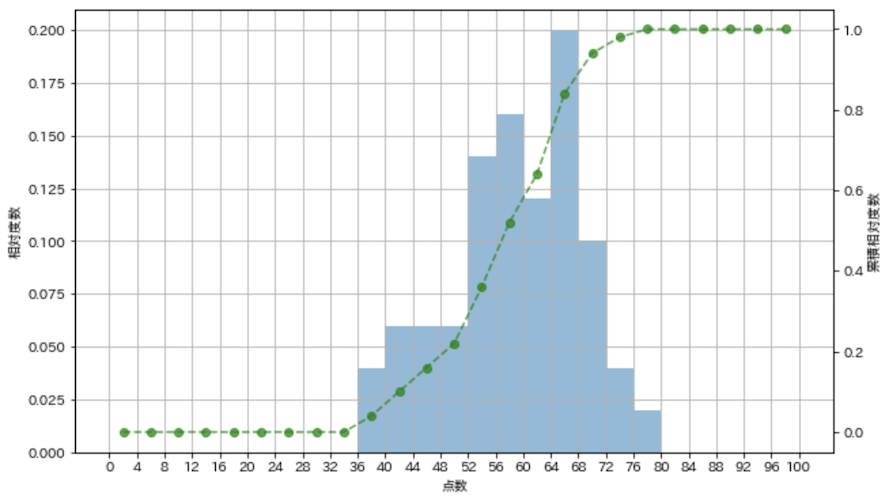
相対度数と累積相対度数のグラフ
fig = plt.figure(figsize=(10, 6))
ax1 = fig.add_subplot(111)
ax2 = ax1.twinx()
weights = np.ones_like(english_scores) / english_scores.shape[0]
rel_freq, _, _ = ax1.hist(english_scores, bins=25, range=(0, 100), weights=weights, alpha=0.5)
cum_rel_freq = np.cumsum(rel_freq)
class_values = [(i + (i + 4)) // 2 for i in range(0, 100, 4)]
ax2.plot(class_values, cum_rel_freq, ls='--', marker='o', color='green', alpha=0.7)
ax2.grid(False)
ax1.set_xlabel('点数')
ax1.set_ylabel('相対度数')
ax2.set_ylabel('累積相対度数')
ax1.set_xticks(np.linspace(0, 100, 25 + 1))
ax1.grid(True)
plt.show()
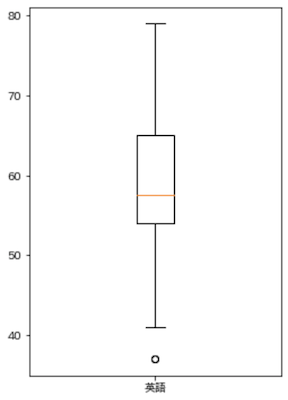
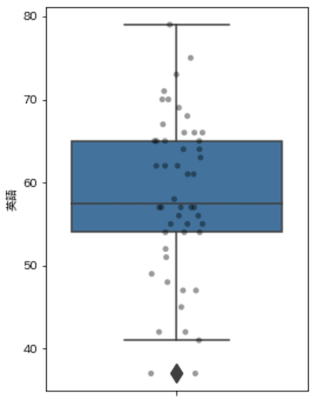
箱ひげ図(Box plot)
データの分布や外れ値を表現することができます.
-
Q1・・・第一四分位数(0.25の分位数) -
Q3・・・第三四分位数(0.75の分位数) -
IQR・・・四分位範囲
上記としたとき,
- 箱・・・
IQRの範囲 - ひげ・・・以下の
A〜Bの範囲-
A・・・MAX(Q1 - 1.5 * IQR, 最小値) -
B・・・MIN(Q3 + 1.5 * IQR, 最大値)
-
- 点・・・外れ値
となります.
plt.figure(figsize=(4, 6))
plt.boxplot(english_scores, labels=['英語'])
plt.show()
seabornでは,外れ値以外の値をプロットしたグラフがよく使われている印象.
import seaborn as sns
english_scores_df = english_scores.to_frame().reset_index()
plt.figure(figsize=(4, 6))
sns.boxplot(y='英語', data=english_scores_df, fliersize=12)
sns.stripplot(y='英語', data=english_scores_df, jitter=True, color='black', alpha=0.4)
plt.show()
箱ひげ図については以下を参照
ライブラリで視覚化された箱ひげ図が「外れ値検出のある箱ひげ図」として紹介されており,通常の箱ひげ図は,5数要約をシンプルに視覚化したもの,とされています.
2次元データ
ここまで1次元データ(英語の点数データ)での様々な指標や視覚化について記載してきました.ここからは,2次元データ(英語と数学の点数データ)を使用して,2つ以上のデータ間の関係性を知る方法を示します.
これまでも使用してきた点数データの最初の10件を使用します.
df = pd.read_csv('data/ch2_scores_em.csv', index_col='生徒番号')
scores_df = df[:10].copy()
scores_df.index = pd.Index(list('ABCDEFGHIJ'), name='生徒')
scores_df
| 生徒 | 英語 | 数学 |
|---|---|---|
| A | 42 | 65 |
| B | 69 | 80 |
| C | 56 | 63 |
| D | 41 | 63 |
| E | 57 | 76 |
| F | 48 | 60 |
| G | 65 | 81 |
| H | 49 | 66 |
| I | 65 | 78 |
| J | 58 | 82 |
相関(Correlation)
2つのデータの関係性を表す指標が,相関です.相関の有無と正負に関して以下にまとめました.
-
正の相関がある
- 英語の点数が高い人は数学の点数が高い
- 英語の点数が低い人は数学の点数が低い
-
負の相関がある
- 英語の点数が高い人は数学の点数が低い
- 英語の点数が低い人は数学の点数が高い
-
無相関である
- 英語の点数が数学の点数に直接影響しない
上記のような言葉でも相関関係を表現できますが,以降は相関関係を定量的に表現する指標について,説明していきます.
共分散(Covariance)
データの偏差を求めて2乗して平均したものが分散ですが,2つのデータの偏差の積(掛け算)を平均したものを共分散といいます.偏差は,点数が平均より高いと正に,平均より低いと負になります.従って,英語と数学の偏差の積は以下のようになります.
| 英語 | 数学 | 偏差の積 |
|---|---|---|
| 低 | 低 | 負 ✕ 負 = 正 |
| 低 | 高 | 負 ✕ 正 = 負 |
| 高 | 低 | 正 ✕ 負 = 負 |
| 高 | 高 | 正 ✕ 正 = 正 |
偏差の積が先にまとめた相関関係と一致していることが分かります!否定排他的論理和 (XNOR) ですね.書籍ではこの辺りを図を交えて解りやすく説明していましたが,私にはこれが限界でした..
実際に偏差の積を求めてみます.
scores_df['英語の偏差'] = scores_df['英語'] - scores_df['英語'].mean()
scores_df['数学の偏差'] = scores_df['数学'] - scores_df['数学'].mean()
scores_df['偏差の積'] = scores_df['英語の偏差'] * scores_df['数学の偏差']
scores_df
| 生徒 | 英語 | 数学 | 英語の偏差 | 数学の偏差 | 偏差の積 |
|---|---|---|---|---|---|
| A | 42 | 65 | -13.0 | -6.4 | 83.2 |
| B | 69 | 80 | 14.0 | 8.6 | 120.4 |
| C | 56 | 63 | 1.0 | -8.4 | -8.4 |
| D | 41 | 63 | -14.0 | -8.4 | 117.6 |
| E | 57 | 76 | 2.0 | 4.6 | 9.2 |
| F | 48 | 60 | -7.0 | -11.4 | 79.8 |
| G | 65 | 81 | 10.0 | 9.6 | 96.0 |
| H | 49 | 66 | -6.0 | -5.4 | 32.4 |
| I | 65 | 78 | 10.0 | 6.6 | 66.0 |
| J | 58 | 82 | 3.0 | 10.6 | 31.8 |
偏差の積を平均して共分散を求めます.
scores_df['偏差の積'].mean()
62.800
正の相関があると言えそうな結果になりました.
共分散行列(Covariance matrix)
Numpyのcov関数で共分散を求めます.
cov_mat = np.cov(scores_df['英語'], scores_df['数学'], ddof=0)
cov_mat = pd.DataFrame(cov_mat, columns=['英語', '数学'], index=['英語', '数学'])
cov_mat
| 英語 | 数学 | |
|---|---|---|
| 英語 | 86.0 | 62.8 |
| 数学 | 62.8 | 68.44 |
NumPyのcov関数で得られる配列は,共分散行列です.マトリクスになっており,英語と英語,数学と数学のセルにはそれぞれの分散が入ります.英語と数学,数学と英語のセルには,両方とも以前求めた共分散の値62.8が入っていることがわかります.
相関係数(Correlation coefficient)
共分散は偏差の積から求められるので,異なる単位の共分散を評価するとき,共分散の値同士を比較することが難しくなってしまいます.単位に依存しない指標を作るために,各偏差を標準偏差で割った上で積の平均をとったものが相関係数です.標準化のときと同じ操作ですね!
en_s = scores_df['英語の偏差'] / np.std(scores_df['英語'])
ma_s = scores_df['数学の偏差'] / np.std(scores_df['数学'])
np.mean(en_s * ma_s)
0.819
最大値が1.0である相関係数で0.819なので,英語と数学の点数はかなり相関が高いと言えそうです.
相関係数の目安については以下を参照.
相関行列(Correlation matrix)
NumPyのcorrcoefでそのまま相関行列を得ることができます.共分散行列のときと戻り値の配列の構成は同じです!
corr_mat = np.corrcoef(scores_df['英語'], scores_df['数学'])
corr_mat = pd.DataFrame(corr_mat, columns=['英語', '数学'], index=['英語', '数学'])
corr_mat
pandasのcorrは2つ以上のデータから一発で相関行列を得ることができます.実行結果は両方とも同じです.
scores_df[['英語', '数学']].corr()
| 英語 | 数学 | |
|---|---|---|
| 英語 | 1.0 | 0.819 |
| 数学 | 0.819 | 1.0 |
英語と英語,数学と数学はすべて同一の値なので,相関係数は共に1.0になっています.
視覚化
ここからは2次元データの関係性を視覚化する方法について説明します.元の50件のデータを使用して描画していきます.
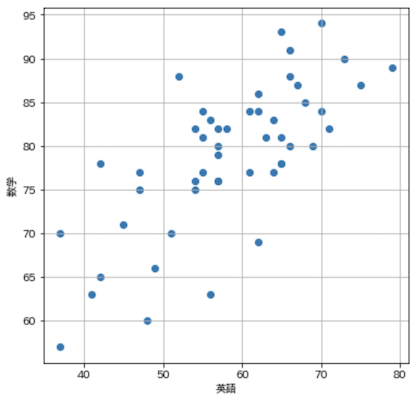
散布図(Scatter plot)
X軸に英語の点数,Y軸に数学の点数を取って,散布図を描画します.
import matplotlib.pyplot as plt
import japanize_matplotlib
plt.figure(figsize=(6, 6))
plt.scatter(df['英語'], df['数学'])
plt.xlabel('英語')
plt.ylabel('数学')
plt.grid(True)
plt.show()
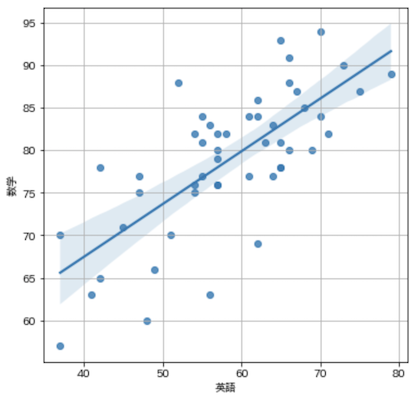
回帰直線(Regression line)
2つのデータの関係性を最も上手く表す直線で表現を回帰直線と言います.matplotlibでは楽に描画できないため,以下はseabornを用いました.
import seaborn as sns
plt.figure(figsize=(6, 6))
sns.regplot(x='英語', y='数学', data=df, fit_reg=True)
plt.grid(True)
plt.show()
回帰直線に関する詳細は以下.
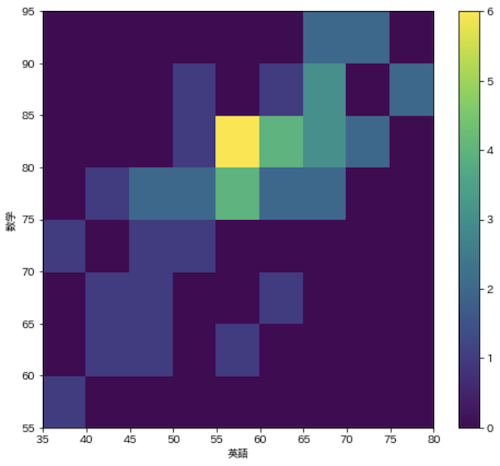
ヒートマップ(Heatmap)
2次元データのヒストグラムや,マトリクスデータを色によって表現するグラフです.今回はhist2d関数を使用して2次元ヒストグラムを描画します.
fig = plt.figure(figsize=(8, 7))
c = plt.hist2d(df['英語'], df['数学'], bins=[9, 8], range=[(35, 80), (55, 95)])
plt.xticks(c[1])
plt.yticks(c[2])
plt.xlabel('英語')
plt.ylabel('数学')
plt.colorbar(c[3])
plt.show()
ヒストグラムは散布図と似た表現なので,マトリクスのデータに対してヒートマップを用いることが多く,個人的にはseabornのheatmapを使用することが多い,,,
seabornのheatmapの詳細は以下
おわりに
長くなりましたが,データ編は以上です.
今回のデータ編については,基礎的な内容のため知っていることも多かったのですが,細かい部分で理解できていなかったことや,知識をそれぞれの点としてではなく,全体を線をなぞるように確認し直せたのは良かったと思っています.少しでも皆さんの参考になれば幸いです.最後まで読んで頂きありがとうございました!
次回,2つ目の確率編はこちらです!