Pythonでちゃんと統計・確率の基礎をやってみた（確率編2/3）

はじめに

以下の書籍を参考にしながら，統計の基礎を学び直した軌跡，確率編2です．

この記事は5部構成の3つ目です．以下も参照ください．

• 準備〜データ編・・・投稿済み
• 確率編1・・・投稿済み
• 確率編2・・・この記事
• 確率編3・・・まだ
• 推測編・・・まだ

この記事を書いた動機，注意点，使用している技術，記事の構成，準備については準備〜データ編に掲載されています．

今回もエンジニアに馴染みの無い用語が沢山出てきます．また，深堀りすればするほど，この技術が何に使えるのか？を見失ってしまい，読み進めるのを諦めてしまいがちです，，，そうならぬよう，書籍を参考にしつつも，補足を入れたり，情報の取捨て選択をしているので，書籍に沿って進めたい方は書籍を購入ください！

確率編2は，確率編1にて学習した離散型確率分布の詳細と，連続型確率分布について一通り学んでいきます．

• 確率編1
  • 推測統計
  • 確率モデル
  • 離散型確率変数
    • 1次元
    • 2次元
• 確率編2
  • 代表的な離散型確率分布
  • 連続型確率変数
    • 1次元
    • 2次元
• 確率編3
  • 代表的な連続型確率分布
  • 多次元確率変数

準備をまとめて実行しておきます．今回新たに，科学計算ライブラリであるSciPyを使用します．

ダウンロードとインストール

!git clone https://github.com/ghmagazine/python_stat_sample.git
!mv ./python_stat_sample/data ./data
!pip install japanize-matplotlib

インポートと設定

import numpy as np
import pandas as pd
from scipy import stats
from scipy.special import comb
from scipy.special import factorial
from scipy import integrate
from scipy import optimize
from functools import partial

import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns

import warnings
warnings.filterwarnings('ignore', category=integrate.IntegrationWarning)

%precision 3
pd.set_option('precision', 3)
pd.options.display.float_format = '{:.3f}'.format

おさらい

限られた標本（データ）から母集団（ターゲット）の統計的特徴を推定し，目的を達成するために活用することが，我々が確率を学ぶモチベーションです．母集団から抽出できる標本が限られる場合，推定する統計的特徴は不確かです．そこで，統計的特徴の推定というタスクを，確率変数の振る舞いの推定，つまり確率分布の推定，というアプローチで進めることにしました．

確率変数がとりうる値を入れると，値の出現確率を返してくれる関数が確率関数です．例えば一般的なサイコロであれば，以下のように確率関数から確率分布を算出できます．

サイコロの確率関数と確率分布

def dice_prob_func(x):
    return 1 / 6

dice_x_set = [1, 2, 3, 4, 5, 6]
dice_prob = np.array([dice_prob_func(x) for x in dice_x_set])

plt.bar(dice_x_set, dice_prob)
plt.ylim(0.0, 1.0)
plt.xlabel('とりうる値')
plt.ylabel('確率')
plt.grid(True)
plt.show()

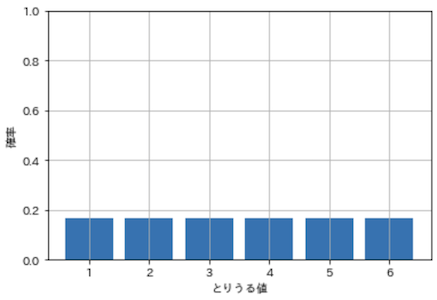
一般的なサイコロは．出目の確率が1/6になることが明白です．しかし，世の中の様々な物事は確率分布が分かっておらず，これを推定することこそが我々の目的であるわけです．

相対度数分布による確率分布の推定

num_trial = 100
dice_sample = np.random.choice(dice_x_set, num_trial)

plt.hist(
    dice_sample, bins=len(dice_x_set), range=(1, 7), density=True,
    label=f'{num_trial}回試行による相対度数分布')
plt.hlines(
    dice_prob, np.arange(1, 7), np.arange(2, 8),
    color='red', lw=3, label='実際の確率分布')

plt.xticks(np.linspace(1.5, 6.5, 6), labels=np.arange(1, 7))
plt.ylim(0.0, 1.0)
plt.xlabel('とりうる値')
plt.ylabel('相対度数')
plt.legend()
plt.grid(True)
plt.show()

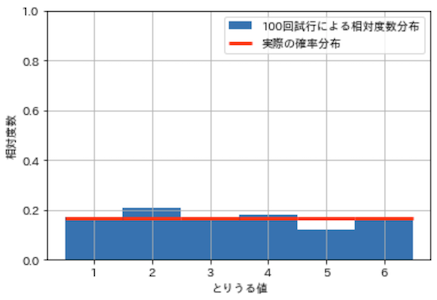
上記は，サイコロを100回投げたときの相対度数分布です．試行を増やすと，相対度数分布は確率分布に収束していきますが，沢山試行する（沢山のデータを得る）のは大変，，，少ない試行で効率良く確率分布を推定する必要があります．

代表的な離散型確率分布

先程挙げた，サイコロを投げた結果から確率分布を推定する方法は，予め確率分布の形状を仮定していません．このような手法をノンパラメトリックな手法，といいます．この手法は，試行を沢山繰り返すことで確率分布を推定することができますが，あまり効率的ではありません..

それに対して，例えばサイコロの形状が正方形であることから，1〜6の出目の確率が大体均等になるだろう，と確率分布のおおよその形状を仮定してから試行を繰り返せば，より少ない試行で確率分布を推定することができます．このような手法をパラメトリックな手法，といいます．

具体的には，試行結果のみに基づいて確率関数を実装するのではなく，まず母集団の性質から確率分布の形状を仮定した上で確率関数を実装します．その上で，確率関数のパラメータを調整して，母集団の確率分布に近づけていきます．パラメータの調整については後日公開予定の記事（推測編）に記載する予定です．

まとめると，以下のようになります．

• ノンパラメトリックな手法
  • 母集団から確率分布の形状を仮定せず確率分布を推定
  • 形状を仮定しない分，確率分布を柔軟に表現できる
  • 正確な確率分布を得るには，沢山の試行結果が必要
• パラメトリックな手法
  • 母集団の性質から確率分布の形状を仮定し，少数のパラメータを調整して確率分布を推定
  • より少ない情報から確率分布を推定することができる
  • 形状を決め打ちするので，確率分布の表現力はノンパラメトリックに劣る
  • 仮定を誤ると確率分布の正確に推定できない可能性が..

書籍の大部分は，後者のパラメトリックな手法についての説明です．パラメトリックな手法を用いるには，どのような場面でどのような確率分布を使用すべきかを知る必要があります．ここからは，代表的な離散型確率分布と，それらがどのような場面で使われるかを学んでいきます！

準備

最初に離散型確率分布の性質を確認するための関数をいくつか用意します．

以下は前記事で学んだ期待値と分散を求める関数です．

期待値と分散の関数

def E(X, g=lambda x: x):
    x_set, f = X
    return np.sum([g(k) * f(k) for k in x_set])

def V(X, g=lambda x: x):
    x_set, f = X
    mean = E(X, g)
    return np.sum([(g(k) - mean) ** 2 * f(k) for k in x_set])

以下は確率変数の性質を満たすか確認した上で，期待値と分散を表示する関数です．

確率変数の性質の確認・表示

def check_prob(X):
    x_set, f = X

    prob = np.array([f(k) for k in x_set])
    assert np.all(prob >= 0), '負の確率があります'

    prob_sum = np.round(np.sum(prob), 6)
    assert prob_sum == 1, f'確率の和が{prob_sum}になりました'

    print(f'期待値: {E(X):.4}, 分散: {V(X):.4}')

最後は確率分布と期待値をグラフで表示するための関数です．

確率分布・期待値・分散のグラフ表示

def plot_prob(X, size=(10, 6)):
    x_set, f = X

    prob = np.array([f(k) for k in x_set])
    e = E(X)

    plt.figure(figsize=size)
    plt.bar(x_set, prob, label='確率')
    plt.vlines(e, 0, 1, label='期待値', color='red')
    plt.xticks(np.append(x_set, e))
    plt.ylim(0, prob.max() * 1.2)
    plt.legend()
    plt.grid(True)
    plt.show()

ベルヌーイ分布（Bernoulli distribution）

とりうる値が0と1しかない，最も基本的な離散型確率分布です．ベルヌーイ分布に従う確率分布の試行をベルヌーイ試行と言い，実現値1を成功，実現値0を失敗と言います．とりうる値が2つしかないため，1が出る確率をpとした場合，もう片方の0が出る確率は1 - pと定まります．つまり，ベルヌーイ分布の形状を調整するために必要なパラメータは，成功（1が出る）確率であるpだけです．

では早速，ベルヌーイ分布の確率関数を作ってみましょう．まずNumPyによる実装，次にSciPyをによる実装を確認していきます．

NumPyによる実装

ベルヌーイ分布の確率関数

def prob_bernoulli(x, p, x_set):
    if x in x_set:
        return (p ** x) * ((1 - p) ** (1 - x))
    else:
        return 0

引数は3つで，値x，先程挙げたパラメータp，とりうる値x_setです．ベルヌーイ分布の場合，x_setは[0, 1]と決まっていますが，関数外でも使用するため，今回は敢えて引数にしています．x_setにxが含まれない場合はelse側で0を返します．if側のコードは無駄にややこしく書いている印象を受けましたが..ベルヌーイ分布の定義をそのまま実装するとこうなるようです．プログラムの詳細を説明します．

例えばpが0.2のとき，プログラムは以下のように動作します．

• 値xが1のとき
  • p ** x・・・0.2の1乗は0.2
  • (1 - p) ** (1 - x)・・・0.8の0乗は1
  • 0.2 * 1 = 0.2・・・0.2を返す
• 値xが0のとき
  • p ** x・・・0.2の0乗は1
  • (1 - p) ** (1 - x)・・・0.8の1乗は0.8
  • 1 * 0.8 = 0.8・・・0.8を返す

1乗と0乗を上手く切り替えることで，出力を制御しています．prob_bernoulliを実行してみます．

ベルヌーイ関数の実行

bern_x_set = np.array([0, 1])
bern_p = 0.2

bern_prob = np.array(
    [prob_bernoulli(k, bern_p, bern_x_set) for k in bern_x_set])
pd.DataFrame(
    bern_prob, columns=['確率'], index=pd.Index(bern_x_set, name='とりうる値'))

とりうる値	確率
0	0.8
1	0.2

1つ目が実現値0の確率で0.8，2つ目が実現値1の確率で0.2になっていますね！もう少し使い勝手を良くするため，ベルヌーイ分布に従う確率変数を返す関数を作りましょう．パラメータpを引数に，とりうる値と確率関数を返します．

ベルヌーイ分布の確率変数を返す関数

def Bern(p):
    x_set = np.array([0, 1])

    def f(x):
        if x in x_set:
            return (p ** x) * ((1 - p) ** (1 - x))
        else:
            return 0
    
    return x_set, f

関数が入れ子になっていて少し分かりにくいですが，ベルヌーイ分布の確率関数であるf(x)を定義し，とりうる値と共に返しています．確率関数の実装は先程のprob_bernoulliと同じものです．同様にp=0.2（成功確率20%）で，確率変数の性質を確認する関数を実行してみます．

確率変数の性質の確認

p = 0.2
X = Bern(p)

check_prob(X)

実行結果

期待値: 0.2, 分散: 0.16

期待値は成功時は1，失敗時0になるので，0.2 * 1 + 0.8 * 0 = 0.2，分散は0.2 * 0.8 = 0.16になります．続いて，確率変数を図示します．

確率変数の図示

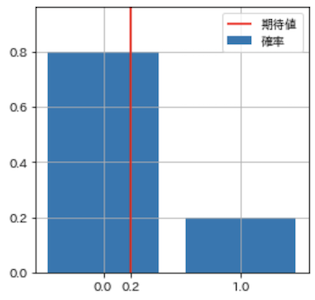
plot_prob(X, size=(4, 4))

ベルヌーイ分布とその期待値の両方が表示できています．

SciPyによる実装

続いてscipy.statsを使用した実装です．scipy.statsには，pを引数にベルヌーイ分布に従う確率変数に相当するオブジェクトを返すbernoulli関数が既に用意されています．

SciPyでベルヌーイ分布に従う確率変数を返す

rv = stats.bernoulli(p)
rv

実行結果

<scipy.stats._distn_infrastructure.rv_frozen at 0x7f913611e990>

このrv_frozenは便利なメソッドを持っています．確率関数（Probability mass function）はpmfで，引数にとりうる値を指定すれば確率が返ってきます．

確率関数

rv.pmf(0), rv.pmf(1)

実行結果

(0.8, 0.2)

とりうる値をリストで渡すこともできます．

リストで渡す

rv.pmf([0, 1])

実行結果

array([0.8, 0.2])

累積分布関数（Cumulative distribution function）はcdf．

累積分布関数

rv.cdf([0, 1])

実行結果

array([0.8, 0.2])

期待値はmean分散はvar．

期待値と分散

print(f'期待値:{rv.mean():.3f} 分散:{rv.var():.3f}')

実行結果

期待値:0.200 分散:0.160

使いどころ

ベルヌーイ分布に従う確率変数は，以下のように様々なケースに当てはめることができます．

• コイン投げで表が出るか
• サイコロを投げて6が出るか
• 広告がクリックされるか
• 来訪者が会員登録を完了するか
• LINEを送って返信が来るか

試行によって得られたデータから簡単に平均（期待値）が計算できるので，我々はベルヌーイ分布を特に意識することなく活用しているのかも，，，加えて，これから紹介する二項分布や幾何分布は，ベルヌーイ試行を何回か繰り返したときに現れる確率分布です．シンプルである分応用の幅が広い，確率分布の基本の1つと言えそうです．

ベルヌーイ分布の詳細については以下

二項分布（Binomial distribution）

成功確率pのベルヌーイ試行をn回行ったときの成功回数が従う分布を，二項分布と言います．パラメータはベルヌーイ分布と同じpと，試行回数nです．とりうる値である成功回数は，1回も成功しない0から，すべて成功するnまでのいずれかです．ちなみに，試行回数nが1のときの二項分布は，ベルヌーイ分布そのものになります！

例えば，表が出る確率が1/2のコインを3回投げたとき，とりうる値（成功回数）は以下になります．

• 成功回数: 0・・・ぜんぶ裏が出る
• 成功回数: 1・・・1回表が出て2回裏が出る
• 成功回数: 2・・・2回表が出て1回裏が出る
• 成功回数: 3・・・ぜんぶ表が出る

これらとりうる値それぞれの確率が，二項分布に従います．ベルヌーイ分布のときと同様に，まず確率変数を返す関数Bin(n, p)を作ります．

NumPyによる実装

二項分布の確率変数を返す関数

from scipy.special import comb

def Bin(n, p):
    x_set = np.arange(n + 1)
    
    def f(x):
        if x in x_set:
            return comb(n, x) * (p ** x) * ((1 - p) ** (n - x))
        else:
            return 0
        return x_set, f
    
    return x_set, f

ベルヌーイ分布の確率関数に似ているので，異なる部分を順番に説明していきます．

ベルヌーイ分布では，とりうる値は[0, 1]でしたが，以下のように[0, 1, 2, ... n]になります．

ベルヌーイ分布のとりうる値

x_set = np.array([0, 1])

二項分布のとりうる値

x_set = np.arange(n + 1)

確率関数の部分では，scipy.special.combという関数を掛け合わせている点と，ベルヌーイ分布では累乗が0と1しかあり得なかったのが，上記のとりうる値の範囲で累乗される数式になっています．ベルヌーイ分布で妙に面倒な計算をしていたのは，二項分布の数式を基にしたからだったんですね，，，

ベルヌーイ分布の確率関数

(p ** x) * ((1 - p) ** (1 - x))

二項分布の確率関数

comb(n, x) * (p ** x) * ((1 - p) ** (n - x))

後半部分は，中学校で習った積の法則です．先程のコインを3回投げたときの例で考えると，成功回数が1のときは表が1回，裏が2回出る確率の積なので，1/2 * 1/2 * 1/2 = 1/8になります．成功回数のとりうる値すべてについて計算すると，以下のようになります．

• 成功回数x = 0・・・(1/2 ** 0) * ((1 - 1/2) ** 3) = 1/8
• 成功回数x = 1・・・(1/2 ** 1) * ((1 - 1/2) ** 2) = 1/8
• 成功回数x = 2・・・(1/2 ** 2) * ((1 - 1/2) ** 1) = 1/8
• 成功回数x = 3・・・(1/2 ** 3) * ((1 - 1/2) ** 0) = 1/8

コインは表と裏が出る確率が同じなので，すべて1/8になります．

前半部分も中学校で習った，組み合わせと和の法則です．3回投げて成功回数が1のときに考えられる組み合わせは，「表，裏，裏」，「裏，表，裏」，「裏，裏，表」の3つなので，確率は1/8 + 1/8 + 1/8 = 3/8になります．scipy.special.combはこの組み合わせを計算してくれる関数です．高校で習うコンビネーション（Combination），${}_nC_r$という奴ですね．とりうる値の確率をすべて計算すると以下のようになります．

• 成功回数x = 0・・・comb(3, 0) * 1/8 = 1 * 1/8 = 1/8
• 成功回数x = 1・・・comb(3, 1) * 1/8 = 3 * 1/8 = 3/8
• 成功回数x = 2・・・comb(3, 2) * 1/8 = 3 * 1/8 = 3/8
• 成功回数x = 3・・・comb(3, 3) * 1/8 = 1 * 1/8 = 1/8

積の法則，和の法則，組み合わせについては以下．

懐かしいですね．当時はこんなもの何の役に立つんだ..と文句ばかり言ってましたが，最近とても役立っています，，，当時の数学の先生ごめんなさい..

Bin(n, p)を使用してコインの例に従う確率変数を作ってみます．

コインを3回投げたとき表が出る回数の確率分布

n = 3
p = 0.5
X = Bin(n, p)

x_set, bin = X
pd.DataFrame(
    [bin(x) for x in x_set],
    index=pd.Index(x_set, name='表が出る回数'),
    columns=['確率']).T

表が出た回数	0	1	2	3
確率	0.125	0.375	0.375	0.125

0.125は1/8，0.375は3/8なので，想定通りの確率分布を作ることができました．同様にサイコロを10回投げて6が出る回数の確率変数を作成してみます．

サイコロを10回投げたとき6が出る回数の確率分布

n = 10
p = 1/6
X = Bin(n, p)

x_set, bin = X
prob = pd.DataFrame(
    [bin(x) for x in x_set],
    index=pd.Index(x_set, name='6が出る回数'),
    columns=['確率'])
prob.T

6が出る回数	0	1	2	3	4	5	6	7	8	9	10
確率	0.162	0.323	0.291	0.155	0.054	0.013	0.002	0.000	0.000	0.000	0.000

期待値と分散は以下のようになります．

期待値と分散

check_prob(X)

実行結果

期待値: 1.667, 分散: 1.389

期待値はn * p = 10 * 1 / 6 = 1.667で，平均の成功回数を表します．これらの統計値はサイコロの出目の期待値や分散ではなく，6が出る回数の統計値である点に注意してください！確率分布と期待値を図示してみます．

確率分布と期待値の図示

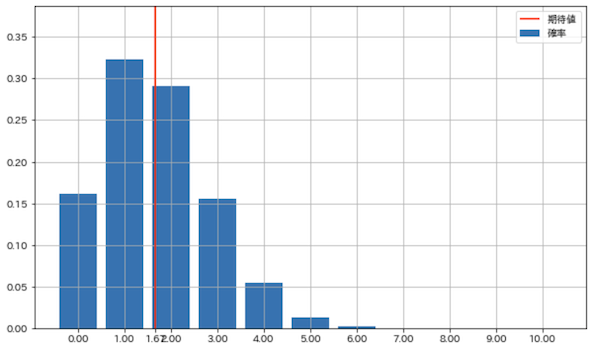
plot_prob(X)

サイコロを10回投げたとき6が出る回数の確率分布と期待値が確認できます．

例えば，3回成功する確率は約15%ということが分かります．また，3回以上成功する確率は，以下のように3回以上の確率を足し合わせれば算出できます．

3回以上成功する確率

prob[prob.index >= 3].sum()

実行結果

確率   0.225
dtype: float64

3回以上成功する確率は，22.5%です！

SciPyによる実装

SciPyではscipy.stats．binom関数を使用するだけで二項分布の確率変数を得ることができます！nを10としたまま，pを0.0〜1.0で変化させて二項分布の形状を確認してみましょう．

n = 10
x_set = np.arange(n + 1)

plt.figure(figsize=(10, 6))
for i in range(1, 10):
    p = i / 10
    
    rv = stats.binom(n, p)
    prob = rv.pmf(x_set)

    plt.plot(x_set, prob, label=f'p:{p}')
plt.grid(True)
plt.xlabel('成功回数')
plt.ylabel('確率')
plt.legend()
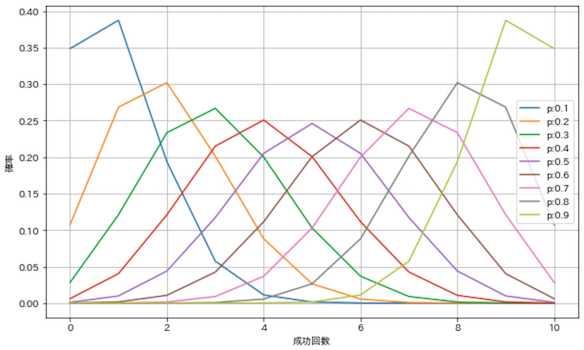
plt.show()

綺麗に左右対称になっていますね．pは成功確率なので，小さくなればなるほど10回試行したときの成功回数が少ない確率が高くなります．逆にpが大きくなればなるほど成功回数が多い確率が高くなります．

使いどころ

ベルヌーイ試行を，複数回行ったときの成功回数の確率分布が二項分布に従う，ということは，ベルヌーイ分布の使いどころで挙げたケースにおいて，成功回数の確率や期待値を求めたいときに役立ちそうです．例えば以下のようなケースを考えることができます．

内定率15%の学生が10社受けたとき，内定が2社以上得られる確率は？

まず，確率分布や期待値を求めます．

内定社数の確率分布

X = Bin(0.15, 10)

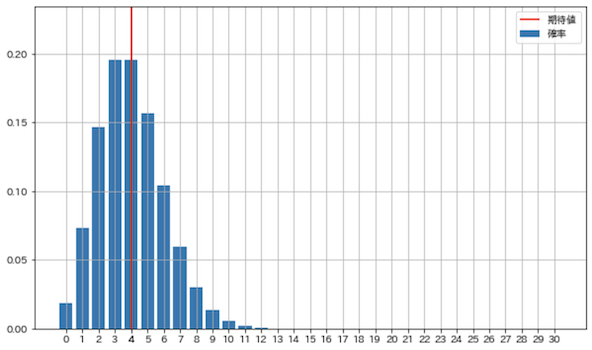
check_prob(X)
plot_prob(X)

実行結果

期待値: 1.5, 分散: 1.275

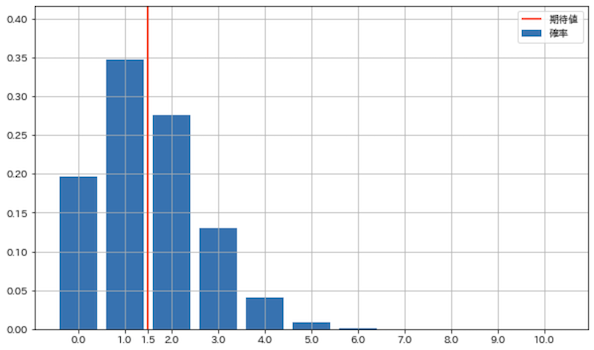
平均で1.5社の内定が期待できるということです．次に内定が2社以上得られる確率を出してみます．

内定が2社以上得られる確率

x_set, bin = X
prob = [bin(x) for x in x_set[x_set >= 2]]
np.sum(prob)

実行時間

0.45570017623447245

内定が1社以下の値をx_setから除外した上で，bin関数に入力しています．約46%なりました！複数の内定から自分が行きたい会社を選びたいのであれば，もっと沢山の採用試験を受けたほうが良いのでは？と考えることができます．二項分布の詳細については以下．

幾何分布（Geometric distribution）

ベルヌーイ試行を繰り返し，初めて成功したときの試行回数が従う確率分布が，幾何分布です．二項分布は一定回数試行したときの成功回数が従う確率分布ですが，幾何分布は一度成功したら終了します．逆に，成功しない限り制限無くベルヌーイ試行を繰り返します．従って，とりうる値は1以上の整数，パラメータは成功確率pだけです．

NumPyによる実装

まず，NumPyで確率変数を実装します．無限のとりうる値を定義できないため，今回は上限の引数を設けて，デフォルト値を100としました．

幾何分布の確率変数

def Ge(p, x_max=100):
    x_set = np.arange(1, x_max + 1)
    
    def f(x):
        if x in x_set:
            return p * ((1 - p) ** (x - 1))
        else:
            return 0
    return x_set, f

幾何分布についても，確率の積の法則に従った簡単な数式です．以下の部分です．

p * ((1 - p) ** (x - 1))

1番左のpは成功する確率です．1回成功したら終わりますが，成功するまで試行を続けるので，必ず1回は必要です．残りの(1 - p) ** (x - 1)は失敗する確率です．1回の成功以外はすべて失敗する確率なので，失敗する確率1 - pの累乗になります．これら2つの積をx回で成功する確率として返します．

pが0.1，xが1〜3のときの確率の計算は以下

• 1回目で成功・・・0.1 * (0.9 ** 0) = 0.1 * 1.0 = 0.1
• 2回目で成功・・・0.1 * (0.9 ** 1) = 0.1 * 0.9 = 0.09
• 3回目で成功・・・0.1 * (0.9 ** 2) = 0.1 * 0.81 = 0.081

2回目で成功するということは，1回成功する確率と1回失敗する確率の積，3回目で成功する場合は，1回成功する確率と2回失敗する確率の積になります．回数を重ねるごとに徐々に確率が下がっていくことが分かります．

では，確率変数を作成してみます．

エラーになる引数..

X = Ge(0.1, x_max=100)
check_prob(X)

実行結果

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
<ipython-input-49-7d57ee186295> in <module>
      1 X = Ge(0.1, x_max=100)
----> 2 check_prob(X)

<ipython-input-5-fc7bec9aca03> in check_prob(X)
      6 
      7     prob_sum = np.round(np.sum(prob), 6)
----> 8     assert prob_sum == 1, f'確率の和が{prob_sum}になりました'
      9 
     10     print(f'期待値: {E(X):.4}, 分散: {V(X):.4}')

AssertionError: 確率の和が0.999973になりました

check_probでエラーになってしまいました..とりうる値を1〜100に制限したため，確率の総和が1.0にならなかった模様..x_maxを1000などと十分に大きくすれば問題無く動作しますが，今回はpを0.2とすることで対処しました．pを大きくすると，回数を重ねたときの確率がより小さくなり，合計が1.0に近づくため，エラーが起こらなくなりました．

幾何分布の性質

X = Ge(0.2, x_max=100)
check_prob(X)
plot_prob(X, size=(24, 4))

実行結果

期待値: 5.0, 分散: 20.0

成功確率20%の試行を成功するまで続けたとき，平均すると5回で成功します．つまり，期待値は1 / pです．

とりうる値を1〜100としたため，めっちゃ横に長いグラフになってしまった，，，試行が多いほど確率が小さくなっていくことがよく分かりますね．

SciPyによる実装

scipy.statsによる実装では，二項分布のときと同様にpを変化させて図示してみます．

SciPyによる幾何分布

x_set = np.arange(21)

plt.figure(figsize=(10, 6))
for i in range(1, 10):
    p = i / 10
    
    rv = stats.geom(p)
    prob = rv.pmf(x_set)

    plt.plot(x_set, prob, label=f'p:{p}')
plt.grid(True)
plt.xlabel('試行回数')
plt.ylabel('確率')
plt.legend()
plt.show()

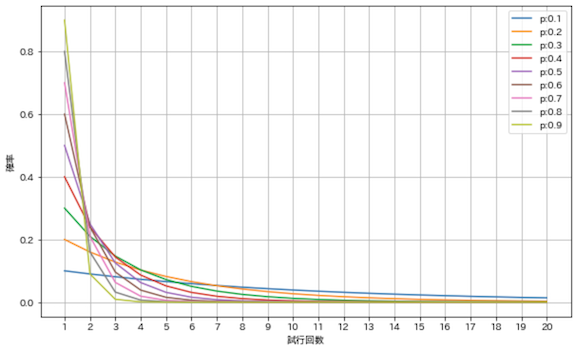
こちらは試行回数が少なくてもエラーにはなりませんでした，，，pが小さければなだらかに，pが大きければ急激に変化しています．成功確率が低ければ沢山試行しないと成功しない，成功確率が高ければすぐ成功して終わるという感覚と一致しますね！

使いどころ

幾何分布もベルヌーイ試行を繰り返しますが，一度でも成功したらそこで試行を終えます．例えば以下のようなケースを考えることができます．

1. サイコロを1が出るまで振ったとき，平均何回で終わるか
2. 当たるまで引ける当選確率2%の宝くじを10回以内に当てる確率は？
3. 継続率が87%の定期購入サービスの平均継続月数

1.は容易にイメージできるかと思います．2.は，10回までの確率分布の和を求めれば良さそうです．

3.の例を少し掘り下げてみます．継続率が87%ということは，解約率は13%です．ユーザーが解約することを一度決心し実行に移したら，そのユーザーに対する定期購入の売上はそこで途絶えてしまいます..つまり，この解約率を幾何分布のパラメータであるpとすれば，成功するまでの試行回数が継続月数，期待値（平均）が平均継続月数になるはず！

では，平均継続月数の算出と，解約の確率分布の図示を行います．

定期購入サービスの解約確率

x_set = np.arange(1, 32)

p = 0.13
rv = stats.geom(p)
pmf = rv.pmf(x_set)
e = rv.mean()
print(f'平均継続月数:{e:.03f}');

plt.figure(figsize=(10, 6))
plt.bar(x_set, pmf, label='解約確率')
plt.vlines(e, 0, 0.15, label='平均', color='red')
plt.grid(True)
plt.xticks(x_set)
plt.xlabel('継続月数')
plt.ylabel('確率')
plt.legend()
plt.show()

実行結果

平均継続月数:7.692

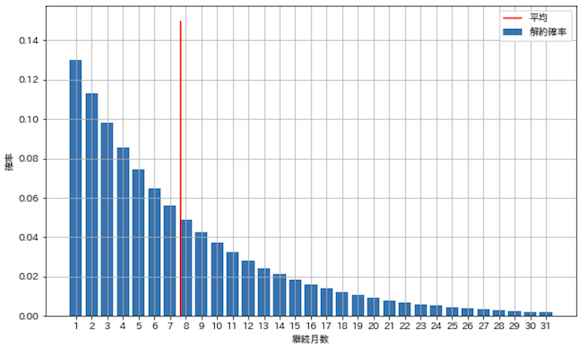
解約率13%のとき平均継続月数は約8ヶ月と求められ，解約の確率分布は上図のようになりました．赤い線として示した平均継続月数は，あくまで期待値（平均）として算出したものであって，解約確率は図のように分布していると考えることができます．実際の解約率pは固定ではなく，ユーザーや継続月数によって変化するケースが多いので，より正確な分布を得るには，もっと深く掘り下げて考える必要がありそうです，，，

この平均継続月数を使うと，例えば月額1000円のとき，LTV（Life time value:顧客生涯価値）を，1000 * 7.692 = 7692円と求めることができます．継続率のお話は以下のパチンコの例がわかり易かった，，，

幾何分布の詳細については以下

ポアソン分布（Poisson distribution）

事象が単位時間あたりにランダムに発生するとき，発生件数が従う確率分布がポアソン分布です．とりうる値は発生回数である0以上の整数です．引数は単位時間辺りの発生件数 λ（ラムダ）で正の実数，以降はlamとします．単位時間は10分でも10ヶ月でもなんでもOK．

二項分布のパラメータである試行回数nと成功確率pの積が平均成功回数ですが，これがポアソン分布でのlamにあたります．言葉で表現しにくいのですが，一定期間常にベルヌーイ試行している状態で，何件か成功が発生するイメージ．つまりnが十分大きく，pが十分小さい状態です．このとき，n * pは一定期間辺りの発生件数として1つの数値で表すことができ，ポアソン分布ではこれを引数としているわけです！

NumPyによる実装

では実装を行います．

ポアソン分布の確率変数

from scipy.special import factorial

def Poi(lam, x_max):
    x_set = np.arange(x_max)
    
    def f(x):
        if x in x_set:
            return np.power(lam, x) / factorial(x) * np.exp(-lam)
        else:
            return 0
    return x_set, f 

難しい関数がいくつか出てきましたね..np.powerは累乗を求める関数です．scipy.special.factorialは階乗を求める関数です．そしてnp.expはネイピア数の累乗です．ここでは式の細かい説明は割愛しますが，二項分布からポアソン分布を導出することができます．詳細は以下．

確率変数を作成して性質を確認します．

ポアソン分布の性質

lam = 4
X = Poi(4, x_max = 30)

check_prob(X)

実行結果

期待値: 4.0, 分散: 4.0

二項分布と同様に期待値はn * pなので，そのままlamの値になります．確率分布を図示してみましょう．

ポアソン分布の図示

plot_prob(X)

SciPyによる実装

scipy.stats.poissonでポアソン分布の確率変数を作ることができます．

lamを変化させたときのポアソン分布

x_set = np.arange(31)

plt.figure(figsize=(10, 6))
for lam in range(1, 20, 2):
    rv = stats.poisson(lam)
    prob = rv.pmf(x_set)

    plt.plot(x_set, prob, label=f'lam:{lam}')
plt.grid(True)
plt.xlabel('発生件数')
plt.ylabel('発生確率')
plt.legend()
plt.show()

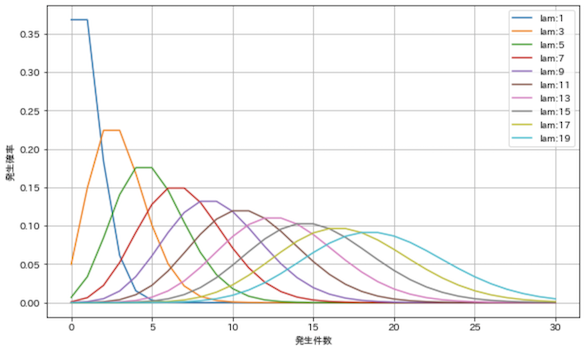
lamを1〜19で変化させて図示しました．単位時間辺りの発生件数lamを大きくするほど分布が広がっています．また，確率の最大値がlamに一致します．例えば以下のようなケースが考えられます．

使いどころ

ポアソン分布は，試行のタイミングが明確ではないが，一定期間にランダムに発生する事象について，その発生回数が従う確率分布です．例えば以下のようなケースを考えることができます．ただし，一定期間辺りの発生件数には平均を用いているので，時間帯やトレンドを考慮したい場合は，発生件数の変化を考慮に入れる必要があります．

1. 年間0.61人が馬に蹴られて死亡する軍隊において，年間何人が馬に蹴られて死ぬか
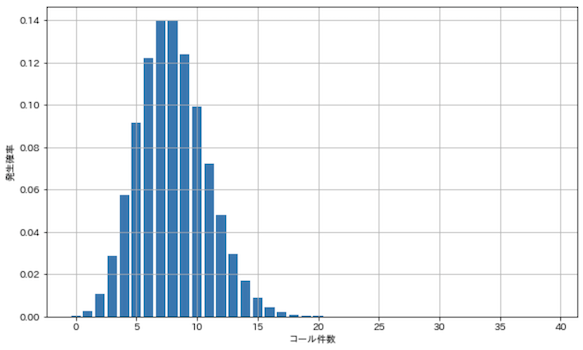
2. 15分の間に平均8件電話がかかってくるコールセンターにて，15分間に17件以上かかってくる確率

1.は歴史的に有名な事例らしいです．図示してみました．

年間で落馬で死亡する人数の確率分布

x_set = np.arange(11)
lam = 0.61

rv = stats.poisson(lam)
prob = rv.pmf(x_set)

plt.figure(figsize=(10, 6))
plt.bar(x_set, prob)
plt.grid(True)
plt.xlabel('死亡件数')
plt.ylabel('発生確率')
plt.show()

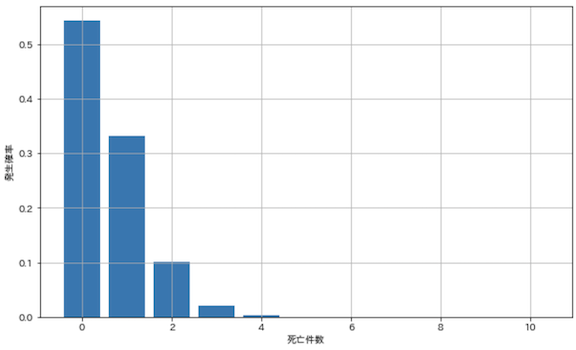
平均発生件数が1.0未満のケースでも，問題無く確率分布を出すことができていますね．

2.は現代でも役立ちそうなケース．

コールセンターのキャパシティ

x_set = np.arange(40)
lam = 8

rv = stats.poisson(lam)
prob = rv.pmf(x_set)

plt.figure(figsize=(10, 6))
plt.bar(x_set, prob)
plt.grid(True)
plt.xlabel('コール件数')
plt.ylabel('発生確率')
plt.show()

17件以上の確率を合計してみます．

コールセンターのキャパシティの検証

np.sum(prob[17:])

実行結果

0.0037180212812834303

例えば１人辺り15分で8件電話応対できる人が2名いたとき，電話応対のキャパシティは16件です．この場合，15分辺り約0.37%の確率でキャパシティをオーバーする可能性がある，逆に99.63%はキャパシティ内に収まる，ということが分かります．

電話の向こうにいる大勢の人が，何をどのタイミングで何回試行しているのか，試行してどんな問題が発生したのか，電話がかかってこない限り，コールセンター側は知ることができません．しかし，一定時間に何件電話がかかってきたか，という情報は容易に得ることができます．ポアソン分布を使うことで，その情報から上記のような分析が可能になるのです！

他にも機器の故障や，多チャネルで販売されている商品の購入など，試行回数の把握が難しいケースで活用されているようです．ポアソン分布の詳細は以下

連続型確率変数

ここまで離散型の確率変数を扱ってきましたが，ここからは，とりうる値が連続的な確率変数について説明します．離散型の確率変数は，とりうる値が飛び飛びの点なので，対応する確率分布も飛び飛びの点になります．一方，連続型の確率変数では，とりうる値が連続した線なので，対応する確率も連続した線になります．

面積と積分

例えばサイコロであれば，2か3が出る確率は，1/6 + 1/6で1/3で，飛び飛びの確率を足せば求めることができます．一方で，連続型の確率変数では，とりうる値が連続しているので，2と3の間に2.5や2.999といったとりうる値が無限に存在するため，とりうる値に対応する確率を足して求めることができません，，，

そこで，2〜3というように，とりうる値の範囲を指定して，その部分の確率分布の面積を求めることで，とりうる値が指定した範囲に収まる確率を算出することができます！面積を求める手法として，高校のときに習った積分（Integral）を用いています．積分に関する数学的な説明は省略します．

積分というワードを敬遠する方がいるかもしれませんが，連続型確率分布において，とりうる値の範囲の面積を計算することで確率を求めることができる，ということが理解できれば，問題無く読み進めることができるかと思います．

積分に関する簡単な説明は以下

1次元

連続型確率変数の説明は，確率編1で説明した離散型確率変数と同じ構成になっています．積分を用いたり，使用する計算式は離散型と違いますが，確率分布の考え方は同じですので，離散型と見比べながら確認すると理解しやすいかもしれません．

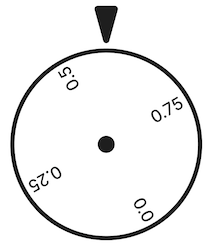
1次元の連続型確率変数では具体例として連続型いかさまルーレットを考えることにします．値を指し示す針があり，ルーレットをくるくる回します．円は1周の長さを1.0とし，ルーレットが止まったときの始点から針までの弧の長さを出目（実現値）とします．つまり，ルーレットのとりうる値は0.0〜1.0の間の実数になります．そして，離散型確率変数の際に扱った「いかさまサイコロ」と同様に，大きい値ほど出やすい，といういかさま仕様です，，，

以下のようなイメージ．

さて，ルーレットを回して↑のようになる確率を考えてみましょう．0.58..辺りでしょうか，，，通常の離散型ルーレットのように出目がはっきり区切られていれば，値を定めることができますが，連続型ルーレットには区切りが存在しないため，値が無限に存在します．無限に存在する値の確率が0より大きいと，確率の合計が1.0になるという，確率変数の条件を満たすことができません..仮にとりうる1つの値を指定すると，確率は0になってしまいます．

そこで連続型確率変数では，とりうる値を区間として指定し，その区間に入る確率を考えます．例えば，ルーレットが0.5〜0.7を指す確率は，0.3といった感じです．

確率密度関数／密度関数（Probability denssity function／PDF）

離散型確率変数は，とりうる値と確率質量関数（確率関数）で定義できましたが，連続型確率変数は，とりうる値の区間と確率密度関数（密度関数）で定義します．ここで重要なのは，確率密度関数と確率質量関数の違いです．確率密度関数はとりうる値の確率を返すわけではなく，とりうる値の確率密度を返します！

これを理解するには，関数の名前にもあるように，質量と密度の違いを考える必要があります．中学生の頃に習った公式を思い出してみましょう．

体積 * 密度 = 質量

同じ体積の鉄と木材では鉄のほうが重い．何故なら，鉄の密度が高いからです．質量は体積と密度を掛け合わせて求めることができます．質量と体積の関係については以下．

確率もこれと同じように考えると，以下のようになります．

とりうる値の区間 * 確率密度 = 確率

とりうる値の区間と確率密度をかけ合わせることで，とりうる値がその区間内に収まる確率を求めることができます．離散型はとりうる値が飛び飛びなので，区間がありません．なので，値から直接確率を算出することができます．一方で連続型は値が連続しているため，値から直接確率を算出しようとすると，ルーレットの例で挙げたようにすべて0になってしまいます．そこで，とりうる値の相対的な出やすさである確率密度を返す関数を定義し，確率密度ととりうる値の区間の面積を確率として表現しているのです！

ここからは，いかさまルーレットを例にして密度関数を実装していきます．まず，とりうる値の区間を定義します．

いかさまルーレットのとりうる値の区間

x_range = np.array([0, 1])

最低値と最大値を指定しています．

次に密度関数を定義します．

いかさまルーレットの密度関数

def f(x):
    x_min, x_max = x_range
    if x_min <= x <= x_max:
        return 2 * x
    else:
        return 0

xがx_rangeの範囲内であるとき，2 * xを返し，それ以外は0を返します．いかさまサイコロのときと同様に，xが増えるほど大きい確率を返す仕組みになっていますが，2をかけているのは，確率の性質である，全確率の総和を1.0にするための工夫です．

では，確率変数を定義して密度関数を図示してみましょう！

密度関数と出目が0.5〜0.7になる確率

X = [x_range, f]

x_min, x_max = x_range
x_s = np.linspace(x_min, x_max, 100)

x_fill = np.linspace(0.5, 0.7, 100)

plt.figure(figsize=(10, 6))
plt.plot(x_s, [f(x) for x in x_s], label='確率密度関数')
plt.fill_between(x_fill, [f(x) for x in x_fill], label='確率', alpha=0.3)

plt.grid(True)
plt.xlabel('とりうる値')
plt.ylabel('密度')
plt.legend()
plt.show()

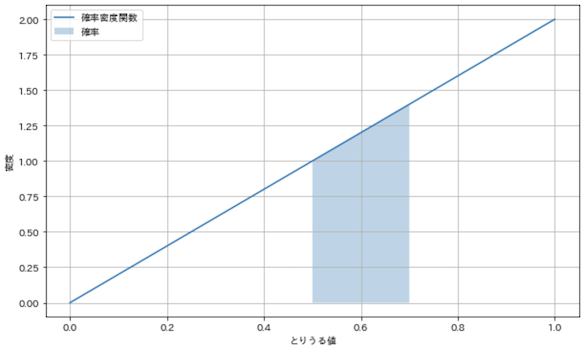
x_sやx_fillは，グラフを描画するためだけに使用する配列です．いかさまルーレットの出目が0.5〜0.7の範囲内に収まる確率の領域を塗りつぶしています．離散型では縦軸が確率になっていましたが，連続型では，縦軸は確率密度を表しており，塗りつぶされた領域の面積が確率になっている点に注意してください！

とりうる値と確率密度が得られたので，塗りつぶした領域の面積（確率）を求めていきましょう．積分にはscipy.integrate.quadを使用します．

いかさまルーレットの確率分布の面積

integrate.quad(f, 0.5, 0.7)

実行結果

(0.240, 0.000)

積分値と推定誤差を返してくれます．確率は0.24と出ました．台形の面積を求める公式を使って，積分によって得られた確率が正しいか，確認してみます．区間は0.5〜0.7なので，台形の高さは0.2，上底は1.0，下底は1.4なので，

(1.0 + 1.4) * 0.2 * 0.5 = 2.4 * 0.1 = 0.24
おお〜積分の結果と台形の面積が一致しましたね！

確率の性質は離散型と同じで，すべて0.0以上，総和は1.0になります．

確率の性質

f_min = optimize.minimize_scalar(f).fun
f_sum = integrate.quad(f, -np.inf, np.inf)[0]

print(f'最小値: {f_min}')
print(f'総和: {f_sum:.3f}')

実行結果

最小値: 0
総和: 1.000

scipy.optimize.minimize_scalarは関数の戻り値の最小値を求める関数で，確率密度関数の最小値が0になることを求めています．総和は先程使用したscipy.integrate.quadにて，区間を無限大にした積分値を求めることができます．

総和についても，今回のケースだと三角形の面積で求めることができます．とりうる値の区間は1.0，確率密度の高さは2.0なので，

1.0 * 2.0 * 0.5 = 1.0
となり，総和と一致します．例えば密度関数を単にxとした場合，三角形の面積は0.5になってしまい，確率の性質に一致しません，，，確率の性質に一致させるために，密度関数内で2 * xとしていたわけですね！

累積分布関数／分布関数（Cumulative distribution function／CDF）

累積分布関数は，確率変数Xが引数x以下になる確率を返します．こちらは離散型確率変数のときと同じです．

累積分布関数

def F(x):
    return integrate.quad(f, -np.inf, x)[0]

F(0.7)

実行結果

0.490

先程のscipy.integrate.quadを使用して実装しています．例えば，いかさまルーレットが0.7以下になる確率は49%と求めることができます．分布関数を組み合わせることで，区間の指定も可能です．

累積分布関数による区間指定

F(0.7) - F(0.5)

実行結果

0.240

分布関数を図示してみます．

いかさまルーレットの累積分布関数の図示

x_min, x_max = x_range
x_s = np.linspace(x_min, x_max, 100)

plt.figure(figsize=(10, 6))
plt.plot(x_s, [F(x) for x in x_s], label='累積分布関数')

plt.grid(True)
plt.xlabel('とりうる値')
plt.ylabel('確率')
plt.legend()
plt.show()

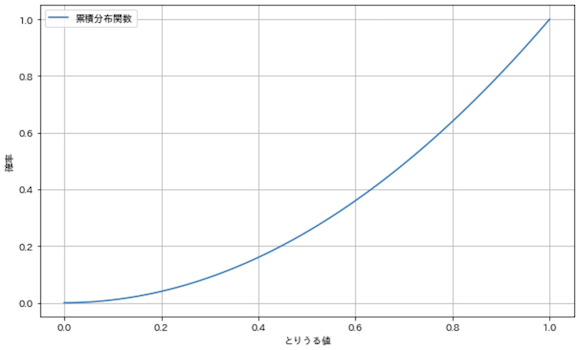
確率を累積しているため，0から始まって，とりうる値の最大値1.0で1.0になっています．確率密度関数と違って，こちらは縦軸が密度ではなく確率になっている点に注意してください．

期待値（Expected value）

連続型確率変数の期待値（平均）です．前記事の離散型確率変数の期待値と同じで，とりうる値と確率の積の総和になります．期待値を求める関数を実装します．

確率の期待値を求める

def integrand(x):
    return x * f(x)

integrate.quad(integrand, -np.inf, np.inf)[0]

実行結果

0.667

いかさまルーレットの密度関数にとりうる値を掛けて，その全面積を求めることで総和を算出できます．これが期待値です．離散型と同じく，期待値を求める関数E(X)を作ります．

期待値を求める関数

def E(X, g=lambda x: x):
    x_range, f = X

    def integrand(x):
        return g(x) * f(x)
    
    return integrate.quad(integrand, -np.inf, np.inf)[0]

E(X)

実行結果

0.667

離散型確率変数の変換のように，確率変数の変換にも対応しています．例えば，いかさまルーレットの出目に対して以下のルールに基づいて報酬を払うことにします．

• 出目の5倍の報酬が貰える
• 参加費用として3取られる

確率変数の変換

E(X, g=lambda x: 5 * x - 3)

実行結果

0.333

引数gに報酬関数を指定することで，期待値を算出することができます！こちらも離散型のときと同様に，線形性が成り立ちます．

期待値の線形性

5 * E(X) - 3

実行結果

0.333

分散（Variance）

連続型確率変数の分散についても，式は離散型の分散と同じです．同様にV(X)を実装します．

分散を求める関数

def V(X, g=lambda x: x):
    x_range, f = X
    mean = E(X, g)

    def integrand(x):
        return (g(x) - mean) ** 2 * f(x)
    
    return integrate.quad(integrand, -np.inf, np.inf)[0]

V(X)

実行結果

0.056

期待値のときと同じようにgを指定してみます．

確率変数の変換

V(X, g=lambda x: 5 * x - 3)

実行結果

1.389

また，離散型でも示した分散の公式は，連続型でも成り立ちます．

分散の公式

5 ** 2 * V(X)

実行結果

1.389

同じ値になりましたね！

2次元

次は2次元の連続型確率変数について扱っていきます．

同時確率密度関数（Joint probability density function）

2つのとりうる値の区間の組み合わせの密度を返す関数が，同時確率密度関数です．離散型の2次元では2つのいかさまサイコロを扱いました．連続型でも２つのいかさまルーレットA，Bを使って考えます．ルーレットAの確率変数をY，ルーレットAとルーレットBの値を足したものを確率変数Xとします．離散型のときと同じように，あとあと共分散や相関係数を求める都合で，２つの変数に関連をもたせています．まとめると以下のようになります．

• X・・・「ルーレットAの値 + ルーレットBの値」の確率変数
• Y・・・「ルーレットBの値」の確率変数

いかさまルーレットのとりうる値の範囲は0.0〜1.0なので，とりうる値x，yのそれぞれの範囲は以下．

• xのとりうる範囲・・・0.0〜2.0
• yのとりうる範囲・・・0.0〜1.0

ここで，同時確率密度関数の実装をどのようにすべきか考えます．書籍では何故か詳しく触れられておらず，いきなり実装の式と条件が出てきて混乱してしまいましたが，，，

最初にルーレットの値を確率変数のとりうる値x，yから逆算します．実装の都合上，いかさまルーレットA，Bそのものではなく，xとyから確率密度を導き出したいためです．x = ルーレットAの値 + ルーレットBの値なので，式変形してルーレットAの値 = x - ルーレットBの値．更に，ルーレットBの値 = yなので，以下のようにルーレットA，Bの値をxとyで表すことができます．

• ルーレットAの値・・・x - y
• ルーレットBの値・・・y

いかさまルーレットの値の範囲は0.0〜1.0なので，

• ルーレットAのとりうる範囲・・・0 <= x - y <= 1
• ルーレットBのとりうる範囲・・・0 <= y <= 1

になります．2つのいかさまルーレットの確率密度は1次元のときの例と同じで，いかさまルーレットの値の2倍です．

• ルーレットAの確率変数・・・2 * (x - y)
• ルーレットBの確率変数・・・2 * y

確率の積の法則から，
2 * (x - y) * 2 * y = 4 * y * (x - y)

従って，確率変数(X, Y)の同時確率密度関数は以下のようになります！

• 0 <= y <= 1かつ0 <= x - y <= 1のとき・・・4 * y * (x - y)
• それ以外のとき・・・0

上記を実装してみましょう．

とりうる値の定義

x_range = [0, 2]
y_range = [0, 1]

同時確率密度関数の定義

def f_xy(x, y):
    if 0 <= y <= 1 and 0 <= x - y <= 1:
        return 4 * y * (x - y)
    else:
        return 0

2次元の確率変数

XY = [x_range, y_range, f_xy]
XY

実行結果

[[0, 2], [0, 1], <function __main__.f_xy(x, y)>]

同時確率密度関数を使って，確率密度の分布をヒートマップで描画します．

確率密度の分布

xr = np.linspace(x_range[0], x_range[1], 200)
yr = np.linspace(y_range[0], y_range[1], 200)
pd_xy = np.array([[f_xy(x, y) for y in yr] for x in xr])

plt.figure(figsize=(10, 8))
sns.heatmap(
    pd_xy, xticklabels=np.linspace(0, 2, 3), yticklabels=np.linspace(0, 1, 3),
    cmap='Blues')
plt.xticks(np.linspace(0, 200, 3))
plt.yticks(np.linspace(0, 200, 3))
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

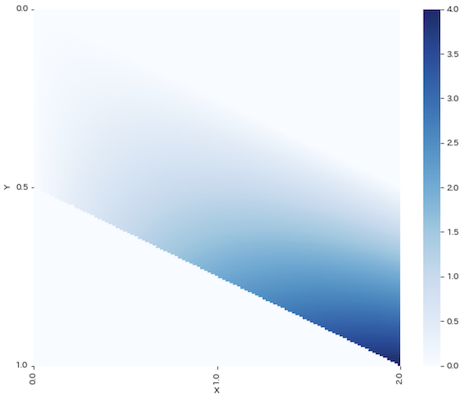
色の濃さが確率の密度を表しています．確率ではなく確率の密度であることに注意してください．右側にあるバーから，確率が必ず0以上になることが分かります．ちなみに離散型のヒートマップに似ていますよね．これは，確率変数の性質が同じだからです．離散型もxはサイコロA + サイコロBの出目で，yはサイコロBの出目なので．

確率の総和は，integrate.nquadで求めます．Xを横軸，Yを縦軸，確率密度を高さとすれば，確率は立体の体積に相当します．

2次元の確率の総和

integrate.nquad(f_xy, [[-np.inf, np.inf], [-np.inf, np.inf]][0]

実行結果

1.000

以上で，確率の条件を満たしていることが確認できました．

周辺確率密度関数（Marginal probability density function）

離散型の周辺分布と同様に，複数の物事からなる確率密度関数から，1つの確率密度の変化だけを抽出した関数を，周辺確率密度関数（周辺密度関数）と言います．離散型のときと同様に片方の引数を固定して求めることができます．

周辺密度関数の定義

def f_X(x):
    return integrate.quad(partial(f_xy, x=x), -np.info, np.inf)[0]

def f_Y(y):
    return integrate.quad(partial(f_xy, ｙ=y), -np.info, np.inf)[0]

f_xyの片方の引数を固定するため，標準ライブラリfunctools.partialを使用しています．片方の引数を固定した確率密度関数をintegrate.quadに指定して，その面積を求めています．それでは，X，Yそれぞれの密度関数を図示してみましょう．

XとYそれぞれの周辺密度関数の図示

X = [x_range, f_X]
Y = [y_range, f_Y]

xr = np.linspace(x_range[0], x_range[1], 100)
yr = np.linspace(y_range[0], y_range[1], 100)

prob_x = [f_X(x) for x in xr]
prob_y = [f_Y(y) for y in yr]

fig = plt.figure(figsize=(16, 6))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)

ax1.plot(xr, prob_x)
ax1.set_title('Xの密度関数')
ax1.set_xlabel('Xのとりうる値')
ax1.set_ylabel('密度')
ax1.grid()

ax2.plot(yr, prob_y)
ax2.set_title('Yの密度関数')
ax2.set_xlabel('Yのとりうる値')
ax2.set_ylabel('密度')
ax2.grid()

plt.show()

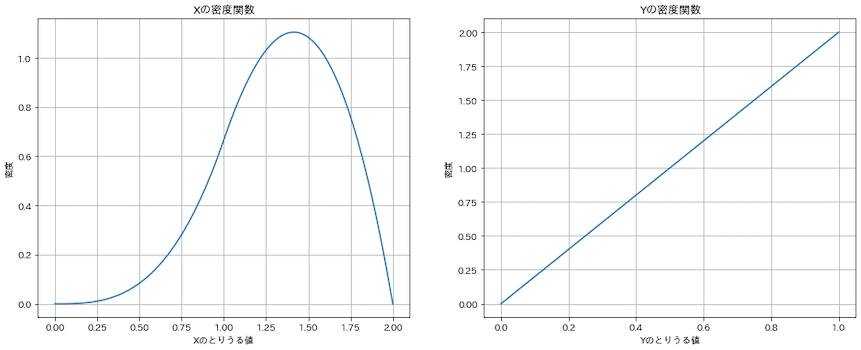
こっちも離散型のときの周辺分布に似ていますね！

期待値（Expected value）

2次元の期待値は1次元のときと同じです．関数E2を定義して，XとYそれぞれの期待値を求めてみます．

2次元の連続型確率変数の期待値

def E2(XY, g):
    x_range, y_range, f_xy = XY
    
    def integrand(x, y):
        return g(x, y) * f_xy(x, y)
    
    return integrate.nquad(integrand, [[-np.inf, np.inf], [-np.inf, np.inf]])[0]

mean_X = E2(XY, lambda x, y: x)
mean_Y = E2(XY, lambda x, y: y)
mean_X, mean_Y

実行結果

(1.333, 0.667)

離散型の2次元の期待値と似たようなコードですね．同様に，期待値の線形性も成り立ちます．

期待値の線形性

a, b = 2, 3

E2(XY, lambda x, y: (a * x) + (b * y)), (a * mean_X) + (b * mean_Y)

実行結果

(4.667, 4.667)

分散（Variance）

分散も1次元のときとほぼ同じです．

2次元の連続型確率変数の分散

def V2(XY, g):
    x_range, y_range, f_xy = XY
    mean = E2(XY, g)
    
    def integrand(x, y):
        return (g(x, y) - mean) ** 2 * f_xy(x, y)
    
    return integrate.nquad(integrand, [[-np.inf, np.inf], [-np.inf, np.inf]])[0]

var_X = V2(XY, lambda x, y: x)
var_Y = V2(XY, lambda x, y: y)
var_X, var_Y

実行結果

(0.111, 0.056)

共分散（Covariance）

共分散はXとYそれぞれの偏差の積の期待値によって求められ．2つの確率変数にどの程度相関があるかを示します．こちらも離散型の2次元の共分散と同じ．

2次元の連続型確率変数の共分散

def cov(XY):
    x_range, y_range, f_xy = XY
    mean_X = E2(XY, lambda x, y: x)
    mean_Y = E2(XY, lambda x, y: y)
    
    def integrand(x, y):
        return (x - mean_X) * (y - mean_Y) * f_xy(x, y)
    
    return integrate.nquad(integrand, [[-np.inf, np.inf], [-np.inf, np.inf]])[0]

cov_XY = cov(XY)
cov_XY

実行結果

0.056

相関係数（Correlation coefficient）

相関係数は，それぞれの分散と共分散から求めることができます．これも離散型の2次元の相関係数と同じです．

2次元の連続型確率変数の相関係数

cov_XY / np.sqrt(var_X * var_Y)

python

0.707

離散型と同じ値になりましたね！！いかさまサイコロA，BといかさまルーレットA，Bの確率変数は本質は同じ確率分布に従っているため，離散，連続の違いはあれどAとBの相関係数も同様の値になるわけです．

おわりに

ここまでを確率編2とします！今回は，代表的な離散型確率分布の紹介と使いどころ，連続型確率変数の基本について記載しました．

Androidエンジニアをやっていた頃は正規分布くらいしか知らなかったのですが，色んな確率分布があり，それぞれの仕組み・用途・関係性を改めて確認することができました．

また，中学・高校の頃に習った確率の和・積の法則や，組み合わせ（コンビネーション），密度と質量，面積と積分など，勉強嫌いだった当時は一生使うことは無いと思っていたものが，数十年後，業務に役立つ技術の理解を助けてくれるとは思いもせず，，，

しかし，記事を書いている自分自身，この考え方は何の役に立つんだ..とか，この数式になんの意味があるんだ..とか，？が沢山浮かんできます．その答えがすべて書籍に書かれているわけもなく，なるべく調べて補足を入れているものの，依然いくつかの疑問は残ったままです．引き続き勉強を続けて，「なるほど！」となったタイミングで記事を修正していければと思います．記事に不備や問題があればいつでもご連絡ください！

次回は確率編のおそらくラストで，代表的な連続型確率分布，多次元確率変数などについて記載する予定です．