はじめに
以下の書籍を参考にしながら,統計の基礎を学び直した軌跡,確率編1/3です.
この記事は5部構成の2つ目になっています.以下も参照ください.
この記事を書いた動機,注意点,使用している技術,記事の構成,準備については準備〜データ編に掲載されています.
これは主観でしかないのですが,エンジニアにも馴染みのある「データ」と比べて「確率」は扱われる機会が少なく,理解のハードルが高いかと思います.引き続き書籍を参考にしながら,理解を助けるために補足したり,独断で省略している部分もありますので,書籍に沿って進めたい方は書籍を購入ください!
また,最初は「確率編」として3部構成を考えていたのですが,確率の基本部分を厚くしたため,以下のように確率編を3つに分けることにしました.
-
確率編1/3
- 推測統計
- 確率モデル
- 離散型確率変数
- 1次元
- 2次元
- 確率編2/3
- 代表的な離散型確率分布
- 連続型確率変数
- 1次元
- 2次元
- 確率編3/3
- 代表的な連続型確率分布
- 多次元確率変数
基本
前記事の構成にて,統計解析のスキルを得るには確率の知識が必要という点に触れましたが,まず,統計解析の全体像から各用語を交えながら掘り下げることで,何故確率の知識が必要なのかを具体的に説明していきます.
記述統計と推測統計
手元にあるデータの統計的性質を記述する枠組みを記述統計と言います.データ編に掲載した内容が,まさに記述統計です.しかし,すべてのデータを手元に揃えて分析できることは稀です.
例えば,Webサイトのアクセス履歴を過去1ヶ月分手元に得たとしても,それはWebサイトを立ち上げてから1ヶ月前までのアクセス履歴や,現在からWebサイトが閉鎖されるまでの未来のデータを含んでいません.仮に我々が過去3ヶ月〜未来3ヶ月の半年間のWebサイトの統計的性質を知りたい場合,手元にある過去1ヶ月分のデータだけを使い,まだ確定していない未来を含めた半年分の統計的性質を推測することになります.
このように,一部のデータから必要なデータ全体の統計的性質を推測する枠組みを推測統計と言い,今回の記事で扱うことにします.
サンプルデータ
上記の例のようなデータを扱うのは複雑なので,書籍と同様に,以下のようなデータを用いて推測統計を説明していきます.
- 全体のデータ・・・高校の全生徒
400人の数学のテスト結果 - 手元のデータ・・・生徒Aさんが聞いて回った
20人分のテスト結果
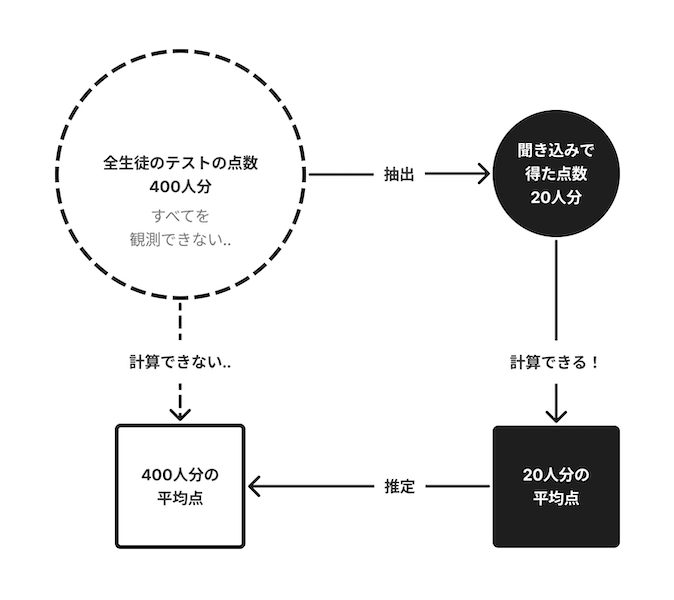
Aさんは高校の生徒で,全生徒のテスト結果を入手できないという制限があります.そんな条件下で,自分の点数の良し悪しを知るため全体の平均点を推測したい!というモチベーション(動機・目的)があります.図にすると以下のような感じ.
もちろん実際に生徒に聞いて回るわけにはいかないので,サンプルデータとプログラムを用います,,,
推測統計の全体像
先程挙げた図が推測統計の全体像になります.が,推測統計を説明する上で必要な用語が入っていないため,各用語を説明しながら当てはめていきます.また,今回の記事のメインである確率の必要性と位置付けについてもお話しします.
準備をまとめて実行しておきます.
!git clone https://github.com/ghmagazine/python_stat_sample.git
!mv ./python_stat_sample/data ./data
!pip install japanize-matplotlib
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
%precision 3
pd.set_option('precision', 3)
実行結果は省略.
母集団(Population)
観測したい対象データ全体のことを母集団と言います.今回のサンプルデータでは400人分の点数が母集団になります.Aさんにとって手に入れることができないデータですが,Aさんによる抽出をシミュレートするため,読み込みます.
all_scores = pd.read_csv('data/ch4_scores400.csv')['点数']
all_scores
0 76
1 55
2 80
3 80
4 74
..
395 77
396 60
397 83
398 80
399 85
Name: 点数, Length: 400, dtype: int64
標本(Sample)
推測に使用する母集団の一部のデータのことを標本と言います.Aさんが手に入れた20人分の点数が,それに当たります.
標本抽出(Sampling)
母集団から標本を取り出すことを標本抽出(Sampling) と言います.Aさんが聞いて回って抽出したことが,それに当たります.
sample_scores = np.random.choice(all_scores, 20, replace=False)
sample_scores
array([55, 65, 69, 58, 63, 57, 86, 61, 50, 54, 64, 64, 65, 86, 48, 82, 75,
50, 64, 58])
上記ではnp.random.choiceによってランダムに標本を抽出する無作為抽出(Random Sampling)を行っています.また,replace=Falseとしているので,同じ標本は一度しか抽出されない非復元抽出です.replace=Trueとすると同じ標本が再度抽出される可能性がある復元抽出になります.また,今回20人としている抽出数のことをサンプルサイズと言います.
ここで,母集団から抽出したデータが偏ってしまう可能性についてに注意してください.例えば,Aさんの知り合い20人に点数を聞いた場合,性別や学年による偏りが出てしまうかもしれません.また,データが偏らないように校内で偶然見かけた人に声をかけたとしても,点数が良くなかった生徒は点数を教えてくれないかも,,,更に,プログラムで行ったように完全にランダムに抽出を行った場合でも,偶然データが偏ってしまうことが考えられます.
データの偏りは,抽出方法を工夫することで軽減できますが,完全には排除できません.推測統計では,このようにサンプルサイズや抽出方法で偏ってしまったデータを適切に扱うことが求められます!
標本統計量(Sampling statistic)
抽出した標本から計算される平均や分散などの統計量です.また,それぞれの統計量のことを標本平均,標本分散などと呼びます.
sample_scores.mean(), sample_scores.var()
(63.700, 119.910)
母数(Parameter)
母集団の統計量(平均や分散など)のことを母数と言います.また,それぞれの統計量のことを母平均,母分散などと呼びます.母集団の全データを手元に得ることは難しいです.従って,母数は直接算出できないことが多いです.
推定量(Estimator)
例えば標本平均から母平均を推測するとき,標本平均は母平均の推定量である,と言います.また,推測された実際の値を推定値と言います.今回の例では,400人の母集団から20人を抽出し,抽出した標本から推定量として標本平均を計算して63.7という推定値が得られたことになります.
確率(Probability)
ここで,無作為抽出と統計量計算を繰り返してみます.具体的には,400人の点数から20人分の点数を無作為に選び,標本統計量を算出して表示する処理を10回繰り返しています.
for i in range(10):
sample_scores = np.random.choice(all_scores, 20, replace=False)
mean, std = sample_scores.mean(), sample_scores.std()
print(f'{i + 1:02}回 平均: {mean:.1f} 標準偏差: {std:.2f}')
01回 平均: 66.7 標準偏差: 14.06
02回 平均: 72.9 標準偏差: 14.74
03回 平均: 76.3 標準偏差: 14.21
04回 平均: 71.2 標準偏差: 17.88
05回 平均: 73.6 標準偏差: 13.00
06回 平均: 64.4 標準偏差: 13.05
07回 平均: 72.5 標準偏差: 14.74
08回 平均: 73.0 標準偏差: 15.70
09回 平均: 70.8 標準偏差: 10.60
10回 平均: 68.7 標準偏差: 13.74
20人の標本抽出だと統計量が結構バラつきますね..標本抽出のところで述べたデータの偏りが影響しています.また,Aさんの例では20人の標本抽出を10回行うのは大変だと思われます..我々は限られた標本から得た推定値の曖昧さ(不確定さ)を定量的に認識する必要があります.
この不確定な現象を考えるときに有効なのが,確率です.確率とは偶然起こる現象の頻度ですが,一連の現象をモデル化して考えることで,今回の例を含む様々な現象の不確定さを定量的に表したり,制御できるようになります!
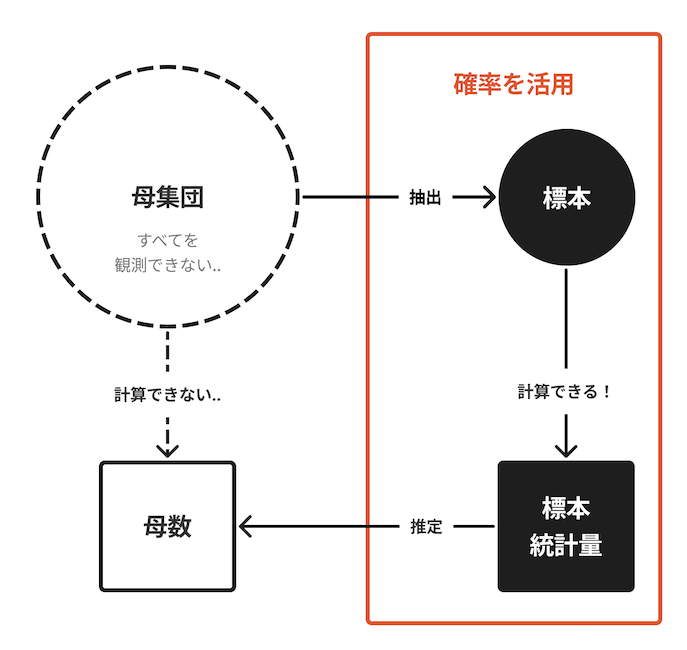
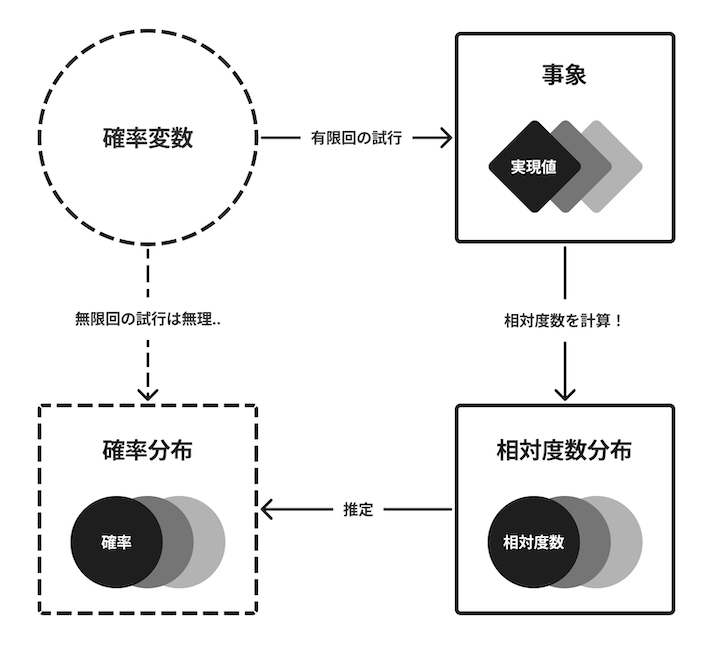
先程示した図を,ここで挙げた各用語に置き換えた全体像が以下です.
図を文章にまとめてみました.
- 母集団全体を観測することができないため,母数は直接計算できない
- 母集団の一部を抽出した標本から標本統計量を計算し,母数を推定することができる
- 標本が偏ることで,推定には不確定さが伴う
- 確率を活用することで,不確定さを定量的に扱い制御することができる
確率モデルの全体像
先程挙げたような不確定な現象を数学的にモデル化したものを確率モデル(Probability model)と言います.これからサイコロを例に用いて確率モデルの全体像を説明していきます.モデル化については以下を参照.
ここで突然サイコロが例として出てきた理由は,確率モデルを考える上で都合が良く,シンプルで誰もが知っているツールだからです.また,世の中の様々な現象を単純なサイコロに置き換えて考えることができます!説明の中で随時例示していきます..
確率変数(Random Variable)
一般的なサイコロを投げたとき,出目は必ず1〜6の数字になります.一般的なサイコロは正方形なので,それぞれの数字が出る確率は同じになります.このように,試してみないと結果はわからないが,とりうる値と値が出る確率が決まっているものを,確率変数と言います.
また変数が出てきましたね..言葉だと理解し辛いですが,プログラムで定義される変数を想像すると分かりやすいかもしれません.以下はサイコロの出目が入る確率変数pを定義しています.
p = np.random.randint(1, 7)
p
2
サイコロの場合,1〜6がそれぞれ同じ確率で入る変数になります.サイコロ以外でも様々な確率変数を考えることができます.
| 説明 | 確率変数名 | とりうる値 |
|---|---|---|
| サイコロ | 出目 |
1,2,3,4,5,6
|
| コイン投げ | 向き |
表,裏
|
| タイタニック | 生き残ったか |
生存,死亡
|
| アプリレビュー | 星の数 |
1,2,3,4,5
|
| テスト | 点数 |
0〜100
|
| ギャンブル | 残金 |
0〜∞
|
| ECサイト | 成果 |
離脱,カートに入れる,購入
|
ここで,確率が決まっていない現象は確率変数なのか,という疑問が浮かびます.例えばコイン投げであれば確率はほぼ半々だと分かっていますが,テストの点数はやってみないと結果が出ません.しかしよく考えてみると,実際にはコインの表面にも微妙に凹凸があって,確率を正確に算出するには無限回コインを投げる必要があります.逆にこれらの現象はすべて,無限回試せば確率を算出することができそうです.
つまり,無限回試したときに確率が確定する現象であれば,それを確率変数として考えることができるはず,,,と,私は解釈したのですが,ちょっと合っているか自信が無いです.正確な確率変数の定義は以下を参照ください.
試行(Trial)
確率変数の結果を得ることが試行です.サイコロを投げると結果(出目)が分かるので,サイコロを投げることが試行に当たります.サイコロを10回投げた結果を得るプログラムが以下です.
[np.random.randint(1, 7) for _ in range(10)]
実現値(Realization)
試行によって観測された値です.サイコロを投げた結果,出目という実現値を得ます.つまり,↑の実行結果が実現値になります.
[1, 1, 6, 5, 2, 3, 2, 4, 5, 2]
事象(Event)
試行の結果として起こりうる出来事を事象と言います.事象の例は以下.
- サイコロの出目が
6 - サイコロの出目が
偶数 - テストの点数が
92点 - 大学受験に
合格! - Webサイトにアクセスがあったが
購入されず..
出目が6は1/6,出目が偶数は1/2のように,確率はそれぞれの事象に対して対応づきます.また,これ以上分解できない出目6や92点などの事象を根本事象(Elementary event)と言います.更に,同時に起こり得ない事象を排反事象(Exclusive event)と言います.ここで重要な確率の性質として,互いに排反な事象において,そのうち少なくとも1つが起こる確率は,各事象の確率の和になる,というものがあります.いつだったか学校で習った和の法則ですね,,,
例えば,サイコロの出目2と出目6は同時に起こり得ないので互いに排反,と言えます.このときそれぞれの出目の確率は1/6なので,出目が2または6となる確率は,
\frac{1}{6} + \frac{1}{6} = \frac{1}{3}
のように計算できます.逆に出目2と 出目偶数は,同時に起こり得るので排反ではなく,上記のような加算は成り立ちません.
確率における和の法則や積の法則については以下
確率分布(Probability distribution)
確率変数がどのような振る舞いをするのか表したものを確率分布と言います.どのような値がどのような確率で出現するか,とりうる値の分布を表します.まず,サイコロの確率分布を作ってみます.
dice_df = pd.DataFrame(index=[1, 2, 3, 4, 5, 6])
dice_df['確率'] = 1 / 6
dice_df.T
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 確率 | 0.167 | 0.167 | 0.167 | 0.167 | 0.167 | 0.167 |
Markdownのフォーマットを少し修正しています..0.167というのは,約1/6です.確率分布を合計すると1.0になります.
dice_df['確率'].sum()
1.000
コイン投げについても同様に確率分布を作りました.
coin_df = pd.DataFrame(index=['表', '裏'])
coin_df['確率'] = 1 / 2
coin_df.T
| 表 | 裏 | |
|---|---|---|
| 確率 | 0.5 | 0.5 |
ここでサイコロとコインの違いについて考えてみましょう.
サイコロは根本事象が6種類,コインは2種類で,それぞれの根本事象の確率はサイコロが1/6で,コインが1/2です.他にも形や投げ方などに違いはありますが,確率モデルとして単純化して考えると,根本事象の数とそれに対応する確率が異なるだけだと分かります.
またサイコロには,コインと同じように1と2しか出目が無いもの,12の出目があるもの(正十二面体)など様々な種類があります.サイコロの種類については以下.思った以上に多種ですね,,,
つまり,コインもサイコロの1つだと捉えることができます.更に,これまで例に挙げた世の中の物事について,何らかの形をしたサイコロを投げた結果だと考えることもできそうです.言い換えると,これまで例に挙げた様々な物事を確率モデルとして捉えることができる.そこから確率分布を導き出すことが,様々な物事を理解するのに役立ちそうです!
ただし,サイコロやコインのように最初から確率分布が判明しているケースは稀です.完全な確率分布を得るには,試行を無限回繰り返してそれぞれの根本事象に対応する確率を確定する必要がありますが,それは現実的ではありません..
度数分布と確率分布
そこで,試行を有限回繰り返して得られたデータから相対度数分布を作り,そこから確率分布を推測する,というアプローチを取ります.
相対度数については前記事のこちらを参照ください.
このアプローチが有効であるかを確認するため,いかさまサイコロを用いた検証を行います.いかさまサイコロは重心がズレており,各出目(1〜6)がどの確率で出るかが偏っています.このいかさまサイコロを繰り返し投げて,確率分布を推測していきます!
roll_index = pd.Index([1, 2, 3, 4, 5, 6], name='出目')
loaded_dice_df = pd.DataFrame(index=roll_index)
loaded_dice_df['確率'] = [1/21, 2/21, 3/21, 4/21, 5/21, 6/21]
loaded_dice_df
| 出目 | 確率 |
|---|---|
| 1 | 0.048 |
| 2 | 0.095 |
| 3 | 0.143 |
| 4 | 0.190 |
| 5 | 0.238 |
| 6 | 0.286 |
上記がいかさまサイコロの確率分布です.出目が大きいほど確率を高く設定しています.この確率分布は試行のシミュレーションに使うだけで,我々にこの確率分布を知ることはできない,とします.
いかさまサイコロ(確率変数)の試行にはnp.random.choiceを使用し,上記の確率分布に従って試行を繰り返します.
num_trial = 100
sample = np.random.choice(loaded_dice_df.index, num_trial, p=loaded_dice_df['確率'])
sample
array([5, 5, 4, 2, 6, 5, 4, 2, 2, 6, 4, 6, 5, 6, 3, 6, 4, 6, 2, 4, 4, 3,
5, 5, 4, 1, 5, 6, 4, 6, 4, 2, 3, 4, 4, 6, 6, 6, 4, 3, 6, 2, 2, 5,
3, 1, 6, 5, 5, 5, 5, 6, 1, 6, 6, 5, 4, 3, 5, 6, 6, 6, 3, 5, 2, 5,
6, 6, 5, 5, 4, 3, 2, 4, 4, 2, 5, 4, 6, 2, 3, 2, 3, 3, 5, 4, 4, 5,
2, 5, 5, 4, 6, 4, 5, 5, 4, 3, 3, 6])
なんとなく出目が大きい数に偏っていてイカサマ臭が..
得られたサンプルデータから度数分布表を作ります.
freq, _ = np.histogram(sample, bins=6, range=(1, 7))
pd.DataFrame({'度数': freq, '相対度数': freq / num_trial}, index=roll_index)
| 出目 | 度数 | 相対度数 |
|---|---|---|
| 1 | 6 | 0.06 |
| 2 | 9 | 0.09 |
| 3 | 13 | 0.13 |
| 4 | 14 | 0.14 |
| 5 | 24 | 0.24 |
| 6 | 34 | 0.34 |
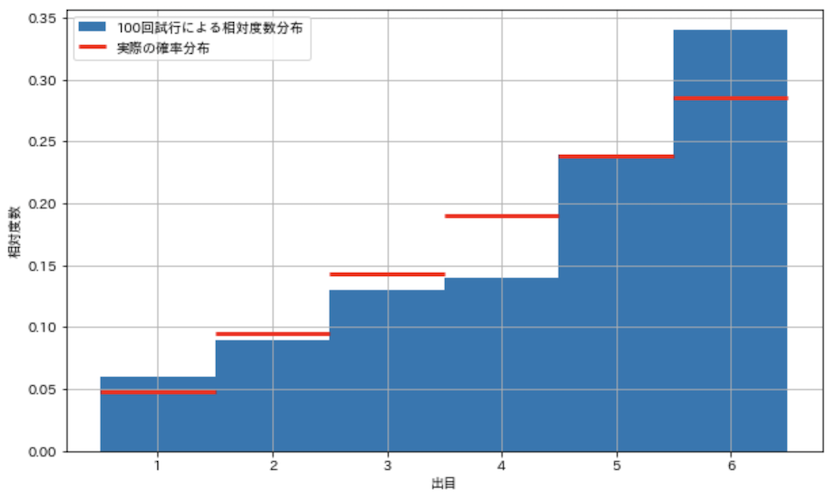
100回試行したときの,それぞれの出目の数と割合が分かりました.いかさまサイコロの実際の確率分布と共に,100回試行したときの相対度数分布をヒストグラムにしてみます.
def show_hist_loaded_dice():
plt.figure(figsize=(10, 6))
plt.hist(sample, bins=6, range=(1, 7), density=True, label=f'{num_trial}回試行による相対度数分布')
plt.hlines(loaded_dice_df['確率'], np.arange(1, 7), np.arange(2, 8), color='red', lw=3, label='実際の確率分布')
plt.xticks(np.linspace(1.5, 6.5, 6), labels=np.arange(1, 7))
plt.xlabel('出目')
plt.ylabel('相対度数')
plt.legend()
plt.grid(True)
plt.show()
show_hist_loaded_dice()
実際の確率分布と相対度数分布を見比べると,傾向は似ているもののまだ差があるように思えます.このグラフの赤い線は,我々が見つけたい実際の確率分布であって,我々には赤い線は不明な状況です.実際の確率分布と,それを推測するために求めた相対度数分布との差を確認するため,敢えて正解データを表示していることに注意してください!
更に試行回数を5000件に増やしてみます.
num_trial = 5000
sample = np.random.choice(loaded_dice_df.index, num_trial, p=loaded_dice_df['確率'])
show_hist_loaded_dice()
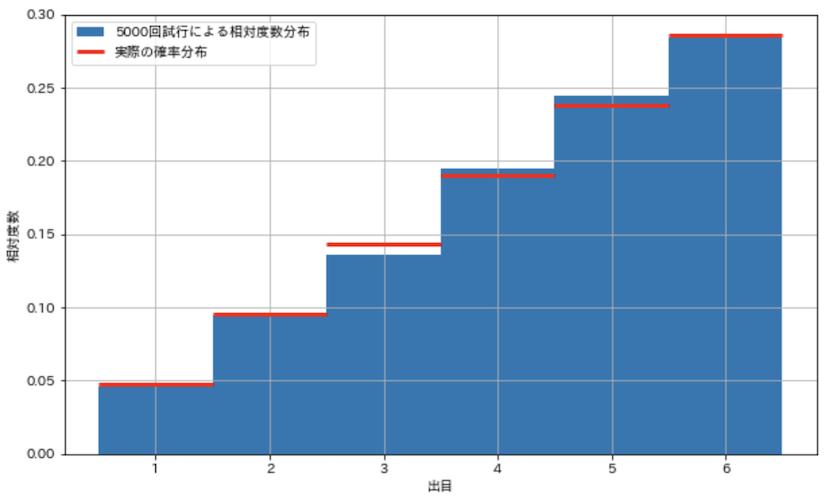
実際の確率分布に近くなってきましたね.この検証から,試行を繰り返して相対度数を求めることで,確率変数の確率分布を推測できそうだ,ということが分かりました.このまま試行回数を増やしていけば,相対度数分布は確率分布に収束していきます.
全体図
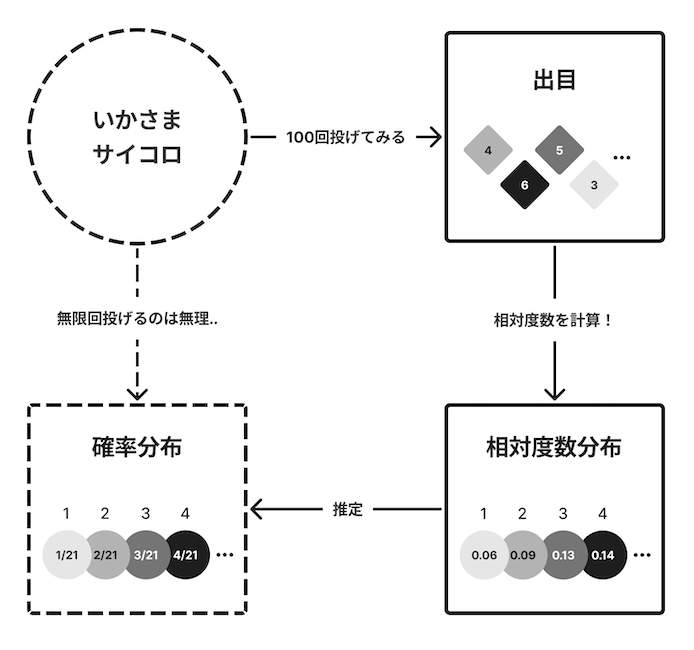
一通り確率モデルについて説明が終わりました.ここで確率モデルの全体図をまとめておきます.まずいかさまサイコロによるこれまでのアプローチを図示してみます.
いかさまサイコロを確率変数としたとき,その確率分布を直接知るには無限回の試行が必要で,実施は不可能です..そこで,サイコロを100回投げて,出目の記録を取って相対度数分布を求めました.そこからいかさまサイコロの真の確率分布を推定しよう,というアプローチです.
いかさまサイコロを一般的な用語に置き換えたものが以下です.
アプリレビューやWebサイトへのアクセスなど,様々な現象を確率変数として考えることで,同様のアプローチが可能になります.また,この図と推測統計の図は構成が似ています,,,どちらも左側の要素のすべてを観測することはできない,ということが大前提になっています.今回参考にしている書籍を読んだタイミングではないのですが,ここからの個人的な学びとして,
- 事実は真実ではない
- 事実を解釈して真実を推定するしかない
という思想を得ました.上図において,事実は右側,真実は左側です.これは拡大解釈し過ぎかもしれませんが,機械学習やデータ分析だけでなく,自分の人生にも影響を及ぼしていたりします..
推測統計と確率モデル
基本の最後に,推測統計の説明に用いた点数の無作為抽出の例を確率モデルで考えてみます.母集団から無作為抽出によって得られる標本を,母集団の確率分布に従う確率変数と見なします.ただし,母集団のすべてが観測できない(無限回試行できない)限り,正確な確率分布は算出できません.
まずは全生徒400人分の点数の相対度数分布をヒストグラムで表示します.
def show_hist_scores(s, bins=100):
plt.figure(figsize=(10, 6))
plt.hist(s, bins=bins, range=(0, 100), density=True)
plt.xlim(20, 100)
plt.xlabel('点数')
plt.ylabel('相対度数')
plt.grid(True)
plt.show()
all_scores = pd.read_csv('data/ch4_scores400.csv')['点数']
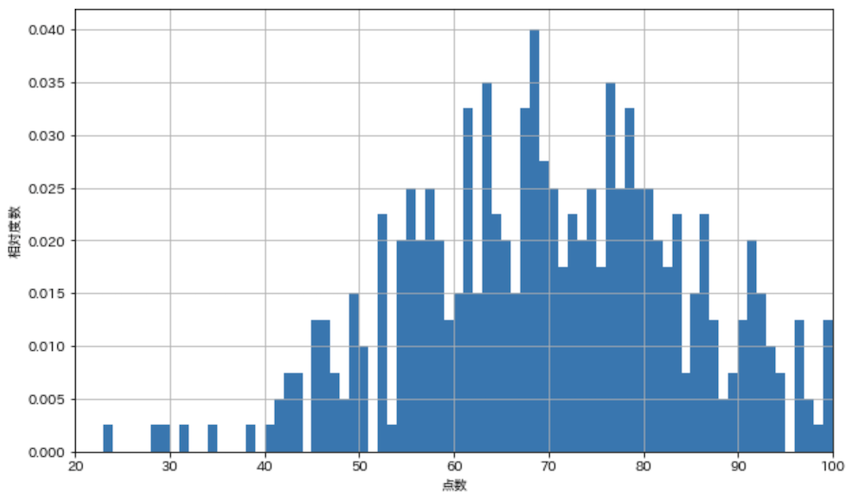
show_hist_scores(all_scores)
この度数分布を母集団の確率分布だと見なすと,例えば70点の人は全体の2.5%を占めているので,無作為抽出を1回試行したとき,70点を得る確率は2.5%だということが分かります.次に試行をシミュレートしてみます.
np.random.choice(all_scores)
76
76点という実現値を得ました.
では,100回試行を繰り返して,同様にヒストグラムを表示してみます.
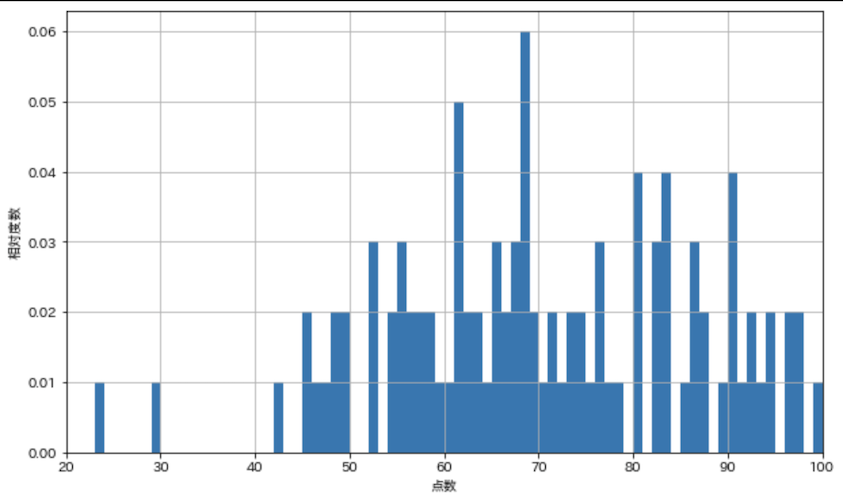
scores = np.random.choice(all_scores, 100)
show_hist_scores(scores)
荒いですが,同じ傾向は見受けられます.今度は試行を10000回にしてみます.
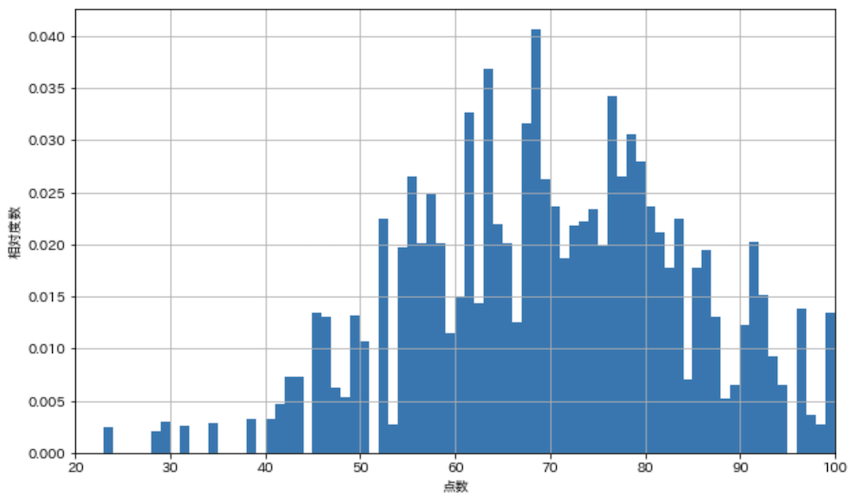
scores = np.random.choice(all_scores, 10000)
show_hist_scores(scores)
ここで注意したいのは,今回のケースでは確率変数が400人のテストの点数だという点です.仮にこのテストを日本中の高校生が受けたとしたら,確率分布は上記とは異なるものになるはず,,,我々が対象とする確率変数や母集団をどう定義するかで,推定すべき確率分布が変わる,ということです.
推測統計と確率モデルの関係をまとめます.
- 推測統計は確率モデルを使って母集団の統計的性質を推測する手法
- 母集団から得られた標本1つ1つが,確率分布に従う確率変数だと見なせる
- 母集団からの無作為抽出は,確率分布に従う確率変数の試行に当たる
- データは結果が確定した値なので,実測値に該当する
母集団を既に結果が確定しているデータと捉えるのではなく,確率分布に従って毎回結果を生み出す歪な形のサイコロだとイメージすると,理解しやすいかもしれません.抽象化され過ぎていて「物事はそんな単純じゃない!」という批判が聞こえてきそうですが,,,物事には色んな捉え方があって,それが有用なら使えば良いんじゃないかと,個人的には思っています.
統計量の確率変数
最後に,統計量を確率変数として捉える例を示します.
Aさんが無作為に20人に声をかけて得た点数の平均を算出
これを1回の試行として捉えると,20人の標本を抽出して算出した平均値を,確率変数の実現値だと考えることができます.それでは,この確率変数が従う確率分布を推定してみましょう.20人分の点数の抽出を10000回シミュレートして相対度数分布を表示しています.
sample_means = [np.random.choice(all_scores, 20).mean() for _ in range(10000)]
plt.figure(figsize=(10, 6))
plt.hist(sample_means, bins=100, range=(0, 100), density=True, label='相対度数分布')
plt.vlines(np.mean(all_scores), 0, 1, color='red', label='母平均')
plt.xlim(50, 90)
plt.ylim(0, 0.15)
plt.xlabel('点数')
plt.ylabel('相対度数')
plt.legend()
plt.grid(True)
plt.show()
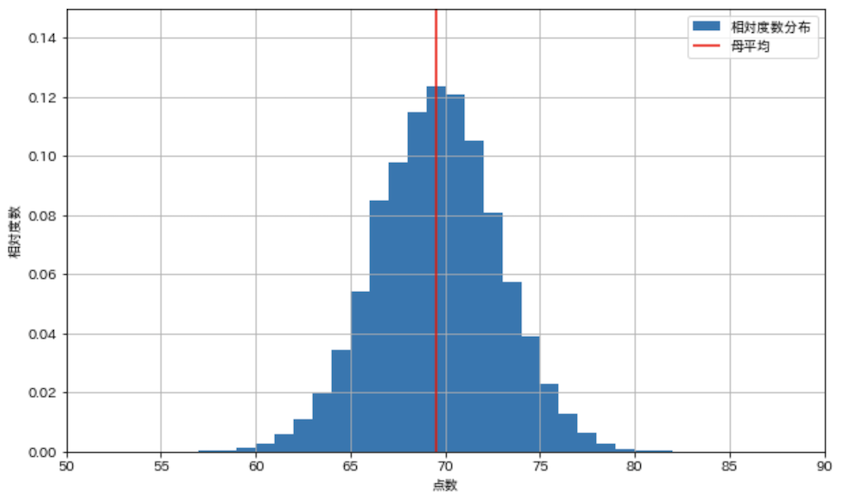
ばらついているものの,母平均を中心に求めた平均値が分布していることから,このシミュレートによって標本平均から母平均が推定できることが分かります.
また,20人の標本抽出だとこのくらい平均値がばらつく,ということが読み取れます.このばらつきは,今実施している分析手法の曖昧さを定量的に表しています.確率モデルを上手く使えば,母集団の統計的性質を推定するだけでなく,分析によって算出された値の曖昧さも定量的に捉えることができます!
離散型確率変数(Discrete random variable)
ここまでは推測統計と確率の基本に触れてきました.ここからは,確率変数の種類や性質についてより詳細に学んでいきます.確率変数はいくつかの種類に分類できます.最初は離散型確率変数から.サイコロの出目やレビューの★の数のように,とりうる値が離散している確率変数です.
ちなみに書籍ではこの辺りから数式の記載が増えています.記事ではなるべく数式は記載せず,プログラムと文章での説明を行っています.繰り返しになりますが,数式が気になる方は書籍を購入ください!
1次元
最初に1次元の確率変数から説明していきます.次元と言われると難しく感じるかもしれませんが,1つの確率変数がある,と考えればOKです.例えば1つのサイコロを,1次元の離散型確率変数,と捉えることができます.
確率質量関数/確率関数(Probability mass function/PMF)
1次元の離散型確率変数を定義するために必要なのは,確率変数がとりうる値と,その値が出現する確率です.2つの値の対応であればPythonのdictを使えば解決しそうですが,今後この対応が複雑になることを考えて,関数で定義することにします.これを確率質量関数,または確率関数と言います.とりうる値の1つを引数として入力したら,確率分布に従った確率を出力する関数です.
いかさまサイコロを例に,最初にとりうる値を作ります.サイコロの出目です.
x_set = np.array([1, 2, 3, 4, 5, 6])
次に確率関数を定義します.
def f(x):
return x / 21 if x in x_set else 0
引数xがx_set内にあるとき, x / 21を確率として返しています.パフォーマンス悪くなりそうですが,21をnp.sum(x_set)としても良さそう.
確率変数は,とりうる値と確率のセットなので,Xとして作っておきます
X = [x_set, f]
大文字で変数に名前を付けるのは違和感がありますが,機械学習のコードだと良く見かけますね.とりあえずその辺りは書籍に合わせています..
確率関数を使用して確率分布を作ります.
prob = np.array([f(x) for x in x_set])
dict(zip(x_set, prob))
{1: 0.048, 2: 0.095, 3: 0.143, 4: 0.190, 5: 0.238, 6: 0.286}
出目が大きくなればなるほど出現確率が増える,いかさまサイコロの確率分布を作ることができました!
そして確率は,すべて0.0以上で,総和は1.0になる性質を持っています.
print(f'すべて0以上: {np.all(prob >= 0)}')
print(f'総和: {np.sum(prob):.3f}')
すべて0以上: True
総和: 1.000
この辺りから,これらが何の役に立つのか解らなくなってきますが,,,例えば営業の電話をかける「架電」を確率変数とした場合,
- 出る
- 出ない
- 話し中
- 留守電
- 未使用の番号
というような,とりうる値(事象)が考えられます.様々な時間帯や曜日,季節における架電結果(確率分布)を知ることは,効率良く架電を行う上で重要な情報になります.試行をシミュレートするための確率変数を定義したり,確率の性質を知ることは,できるだけ少ない試行で架電の確率分布を推定するのに役立つはず..
難しい用語や定義からは用途をイメージし辛いですが,そんなモチベーションで読み進めて頂ければと思います!
累積分布関数/分布関数(Cumulative distribution function/CDF)
確率変数Xが引数x以下になる確率です.とりうる値がx以下の確率を加算して返す関数です.
def F(x):
return np.sum([f(xx) for xx in x_set if xx <= x])
F(4)
0.476
いかさまサイコロを投げたとき4以下が出る確率は,47.6%だ,ということです.
2つの関数から得られる分布は,前記事で挙げた,有限のデータから得られる相対度数分布,累積相対度数分布に似ています.相対度数分布は試行を繰り返すことで確率分布に収束していく,同様に累積相対度数分布は累積の確率分布に収束していくイメージです.
確率変数の変換
ここで,確率変数のとりうる値を置き換える操作について説明します.いかさまサイコロの出目に対して10X - 10の報酬を与える,とした場合,確率変数Xを変換して別の確率変数Yを作ることができます.例えば出目が1なら報酬は0,出目が5なら40になります.この確率変数の確率分布を作ってみます.
y_set = np.array([10 * xx - 10 for xx in x_set])
dict(zip(y_set, prob))
{0: 0.048, 10: 0.095, 20: 0.143, 30: 0.190, 40: 0.238, 50: 0.286}
x_setからy_setを作って置き換えた上で,いかさまサイコロの確率は変わらないため,probはそのまま流用しています.
報酬を変更した上で次項で出てくる期待値を求めるときや,確率変数の標準化(平均を引いて標準偏差で割る)に必要な操作らしいのですが,現状の情報だけではいまいちピンときませんね..少し調べてみたのですが,この段階では,確率変数から別の確率変数を作ったり,確率変数同士の演算ができるよ,くらいの理解で良さそうです.
確率変数の標準化については以下
期待値(Expected value)
確率変数を無限回試行して得られた実現値の平均を期待値と言います.無限回試行することはできませんが,確率変数のとりうる値と確率の積の総和で算出することができます.有限回の繰り返しで得られたデータの平均は,試行を増やしていくと期待値に収束する,ということです.つまり,標本から算出される平均・分散などの指標は,標本が増加するにつれて確率変数の指標に収束していきます!
では,いかさまサイコロの確率変数Xの期待値を計算してみます.
def E(X, g=lambda x: x):
x_set, f = X
return np.sum([g(xx) * f(xx) for xx in x_set])
E(X)
4.333
引数に確率変数Xを入力して,とりうる値と確率の積を算出,np.sumで総和しています.引数にはgという関数を指定できます.デフォルト値はとりうる値をそのまま使用しますが,先程説明した確率変数を変換する関数などを指定することができます.先程の確率変数Y = 10X - 10を指定してみます.
E(X, g=lambda x: 10 * x - 10)
33.333
いかさまサイコロの出目ではなく,出目から計算される報酬の期待値は33.333になりました.
また,期待値は線形性が成り立ちます.
10 * E(X) - 10
33.333
E(X)を求めてから変換を行っても同じ結果になりましたね!関数の線形性については以下
分散(Variance)
データにおける分散と同様に確率変数のばらつきを表します.前記事の分散の記事はこちら.では,いかさまサイコロの確率変数Xの分散を算出してみます.
def V(X, g=lambda x: x):
x_set, f = X
mean = E(X, g)
return np.sum([(g(xx) - mean) ** 2 * f(xx) for xx in x_set])
V(X)
2.222
g(xx) - meanが偏差に当たります.それを2乗し,とりうる値の確率f(xx)との積を算出,更にnp.sumで総和し,確率変数の分散を求めています.期待値のときと同様に,確率変数Yの分散Y = 10X - 10を指定してみます.
V(X, g=lambda x: 10 * x - 10)
222.222
また,期待値のときは線形性が成り立ちましたが,分散の場合は分散の公式が成り立つとのこと.
10 ** 2 * V(X)
222.222
係数10(傾き)を2乗するだけで,切片-10は式から消えていますが,結果は一致しました!公式の説明は割愛しますので,以下を参照ください.
2次元
続いて2次元の離散型確率変数について説明します.2次元というのは,2つの確率変数を同時に扱うということです.前記事の2次元データに似ていますね.1次元のときと同様に,データが無限に存在する(無限回の試行)と考えたときの共分散などが,2つの確率分布から算出できそうです!
同時確率分布/同時分布(Joint probability distribution)
2つの確率変数の振る舞いを同時に考えた分布のことを同時確率分布と言います.2つのいかさまサイコロを同時に投げても,一方の出目がもう一方の出目に影響しません.それでは共分散が0.0になってしまって都合が悪いため,サイコロAの出目をY,サイコロAの出目とサイコロBの出目を足したものをXとして,わざと2つの変数に関連を持たせます.
まとめると,
- サイコロAとサイコロBを同時に投げて出目を確認
-
X・・・サイコロAの出目+サイコロBの出目 -
Y・・・サイコロAの出目
を試行とします.まず,2次元の確率変数がとりうる値を考えます.
x_set = np.arange(2, 13)
y_set = np.arange(1, 7)
print(f'Xのとりうる値: {x_set}')
print(f'Yのとりうる値: {y_set}')
Xのとりうる値: [ 2 3 4 5 6 7 8 9 10 11 12]
Yのとりうる値: [1 2 3 4 5 6]
x_setは2つのサイコロの出目の和なので2〜12,y_setは1〜6になります.この2つの配列の組み合わせが,今回の確率変数のとりうる値です.ではそれぞれの確率はどうなるでしょうか,,,いかさまサイコロの確率分布は以下でした.
| 出目 | 確率 |
|---|---|
| 1 | 1 / 21 |
| 2 | 2 / 21 |
| 3 | 3 / 21 |
| 4 | 4 / 21 |
| 5 | 5 / 21 |
| 6 | 6 / 21 |
この確率分布に従うサイコロA,Bを同時に投げたとき,Aの出目がY,AとBの和がXなので,XからサイコロAの出目を引けば,XのサイコロBの出目が分かります.あとはサイコロAの出目の確率とサイコロBの出目の確率の積が,XとYを組み合わせた確率になります.学校で習った積の法則ですね!
例えば,Xが5,Yが2のとき,サイコロAの出目は2,サイコロBの出目は5 - 2 = 3なので,確率は
\frac{2}{21} \times \frac{3}{21} = \frac{6}{441}
と計算できます.サイコロA,Bの出目からXとYを求めて,そこから確率を算出するほうが直感的ですが,今回サイコロA,Bの出目を加算するところは試行の中で行われていることなので,あくまで試行結果からサイコロBの出目を逆算することにしています.
では,確率分布を作ってヒートマップを表示してみます.
def f_XY(x, y):
a, b = y, x - y
if 1 <= a <= 6 and 1 <= b <= 6:
return a * b / (21 * 21)
else:
return 0
prob = np.array([[f_XY(i, j) for j in y_set] for i in x_set])
prob_df = pd.DataFrame(prob, index=pd.Index(x_set, name='X'), columns=pd.Index(y_set, name='Y'))
plt.figure(figsize=(8, 7))
sns.heatmap(prob_df, annot=True, fmt='1.3f', cmap='Reds')
plt.show()
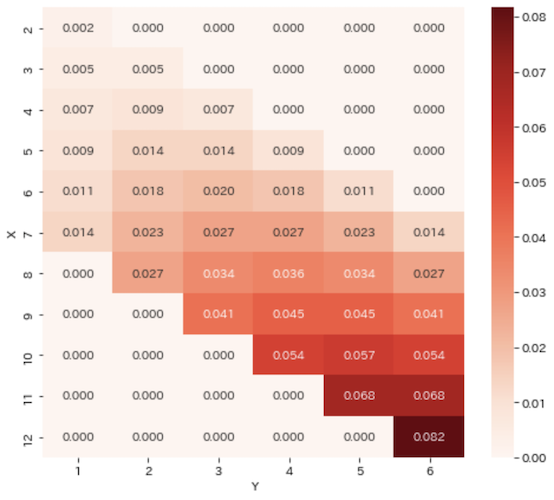
サイコロは1〜6までしか出目が無いため,例えば$Y$が1のとき$X$は8以上になりません.そういったあり得ない確率はすべて0.0になっていますね.そして$X$,$Y$両方の数字が大きくなるにつれて確率が高くなっています.いかさまサイコロらしい傾向です.
2次元でも確率の性質を確認しておきます.
print(f'すべて0以上: {np.all(prob >= 0)}')
print(f'総和: {np.sum(prob):.3f}')
すべて0以上: True
総和: 1.000
1次元のときと同様の結果が得られましたね.
同時確率関数(Joint probability function)
2つのとりうる値を入力として,その確率分布に従った確率を返す関数です.先程定義したf_XYですね.改めて記載して説明します.
def f_XY(x, y):
a, b = y, x - y
if 1 <= a <= 6 and 1 <= b <= 6:
return a * b / (21 * 21)
else:
return 0
引数x,yからサイコロA,Bの出目a,bを求めて,それぞれがサイコロの出目の範囲に収まっているとき,積の法則に従って確率を算出しています.
確率変数XYも定義しておきます.
XY = [x_set, y_set, f_XY]
周辺確率分布/周辺分布(Marginal probability distribution)
複数の物事から成る確率分布に対して,1つの物事による確率分布を周辺確率分布と言います.今回の2次元の確率変数だと,XやYそれぞれの確率分布が周辺確率分布です.例えば2次元の確率変数XYから確率変数Xを取り出すには,確率変数Yの影響を取り除く必要があります.では,XYからXとYを取り出してみましょう.
prob_df.sum(axis=1).to_frame().T
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.002 | 0.009 | 0.023 | 0.045 | 0.079 | 0.127 | 0.160 | 0.172 | 0.166 | 0.136 | 0.082 |
Xのとりうる値それぞれでYのとりうる値の確率を合計すれば,周辺分布を求めることができます.DataFrame.sumを使用しました.Yについても同様に求めます.
prob_df.sum(axis=0).to_frame().T
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| 0.048 | 0.095 | 0.143 | 0.190 | 0.238 | 0.286 |
上記と同じ処理を行う関数を用意して確率変数XとYを作ります.
def f_X(x):
return np.sum([f_XY(x, y) for y in y_set])
def f_Y(y):
return np.sum([f_XY(x, y) for x in x_set])
X = [x_set, f_X]
Y = [y_set, f_Y]
f_XYを使用して,引数ともう一方のすべてのとりうる値の確率を合計しています.作った関数を使用して,それぞれの周辺分布を表示してみます!
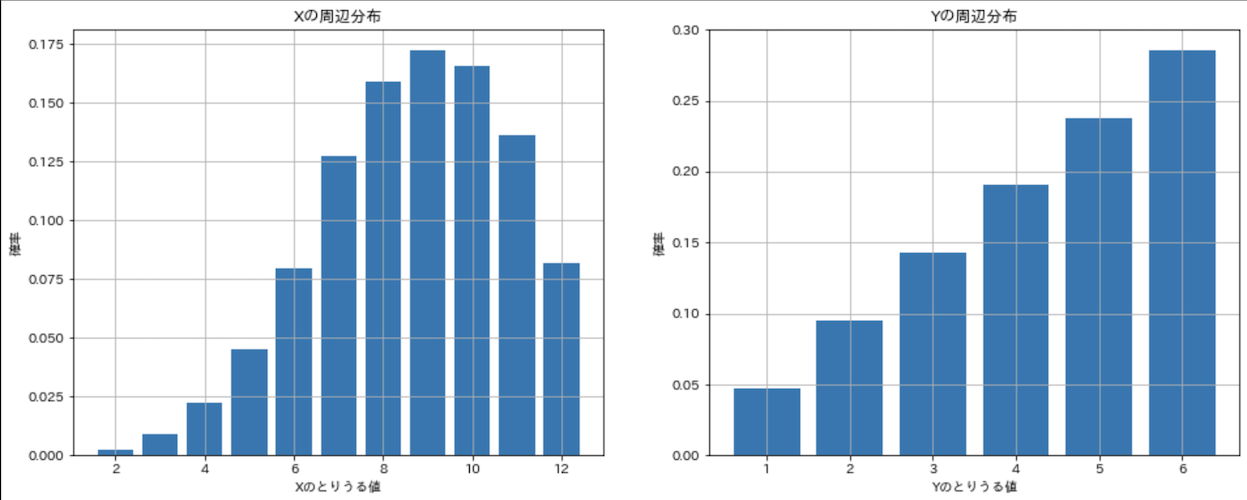
prob_x = np.array([f_X(k) for k in x_set])
prob_y = np.array([f_Y(k) for k in y_set])
fig = plt.figure(figsize=(16, 6))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
ax1.bar(x_set, prob_x)
ax1.set_title('Xの周辺分布')
ax1.set_xlabel('Xのとりうる値')
ax1.set_ylabel('確率')
ax1.grid()
ax2.bar(y_set, prob_y)
ax2.set_title('Yの周辺分布')
ax2.set_xlabel('Yのとりうる値')
ax2.set_ylabel('確率')
ax2.grid()
plt.show()
Xの周辺分布は2つのサイコロの足した数なので,2,12などは出目の組み合わせが少なく,確率が低くなります.しかし,使用しているのがいかさまサイコロなので,若干大きい数に確率の山が寄っているのが分かりますね,,,またYはいかさまサイコロの確率分布そのものになっていることが分かります.
期待値(Expected value)
2次元の確率変数の期待値は1次元と同じです.関数E2を定義してXとYそれぞれの期待値を求めてみます.
def E2(XY, g):
x_set, y_set, f_XY = XY
return np.sum([[g(i, j) * f_XY(i, j) for i in x_set] for j in y_set])
mean_X = E2(XY, lambda x, y: x)
mean_Y = E2(XY, lambda x, y: y)
mean_X, mean_Y
(8.667, 4.333)
関数gでとりうる値そのものを指定して返せば,期待値を求めることができます.例えばここにサイコロの出目に基づく報酬などを設定できるのは,1次元のときと同じですね.x + yとすればXとYの期待値の合計が算出できます,
E2(XY, lambda x, y: x + y)
13.000
1次元のときと同様に期待値には線形性があるため,XとYそれぞれの期待値をE2で算出してから加算しても,結果は同じになります.
mean_X + mean_Y
13.000
分散(Variance)
分散も1次元と同様に,偏差の2乗の期待値によって求められます.
def V2(XY, g):
x_set, y_set, f_XY = XY
mean = E2(XY, g)
return np.sum([[(g(i, j) - mean) ** 2 * f_XY(i, j) for i in x_set] for j in y_set])
var_X = V2(XY, lambda x, y: x)
var_Y = V2(XY, lambda x, y: y)
var_X, var_Y
(4.444, 2.222)
共分散(Covariance)
共分散はXとYそれぞれの偏差の積の期待値によって求められ.2つの確率変数にどの程度相関があるかを示します.データ編の共分散に似ていますね.
def cov(XY):
x_set, y_set, f_XY = XY
mean_X = E2(XY, lambda x, y: x)
mean_Y = E2(XY, lambda x, y: y)
return np.sum([[(i - mean_X) * (j - mean_Y) * f_XY(i, j) for i in x_set] for j in y_set])
cov_XY = cov(XY)
cov_XY
2.222
相関係数(Correlation coefficient)
最後に相関係数です.こちらもデータ編の相関係数と同様で,共分散をX,Yの標準偏差で割って求めます.
def corr(XY):
cov_xy = cov(XY)
var_x = V2(XY, lambda x, y: x)
var_y = V2(XY, lambda x, y: y)
return cov_xy / np.sqrt(var_x * var_y)
corr(XY)
0.707
YはサイコロAの出目,XはサイコロAとBの出目を足したものなので,2つの確率変数には相関が仕組まれています.算出された相関係数は,0.707と,高い相関を示していることがわかります.
おわりに
ここまでを確率編1とします.今回は,推測統計と確率モデルの全体像,1次元と2次元の離散型確率変数について記載しました.
我々の目的に必要な全データと,手元にあるデータが異なる場合,そのデータは母集団から抽出された標本であり,有限回の試行から生み出された実現値の集まりです.無限回の試行(全データ)から得られた確率分布を知ることができれば,我々は目的を果たすことができます.
目的に対するアプローチとして,手元にあるデータからなるべく正確に全データの性質を知ること,全データに対して手元にあるデータの曖昧さを定量的に知ることに,確率モデルが役立つ,ということを学びました.また,データ(有限の試行結果)から得られる統計値は,データを増やしていく(無限の試行結果に近づける)と,データを確率変数と捉えたときの統計値に収束していくことが分かりました.
個人的には,ふわっとした理解しか出来ていなかった確率モデルや,記述統計と推測統計の関係性について整理する良い機会になりましたが,この分野についての実務経験はあまり多くないので,間違っている点などあればご指摘頂ければと思います!最後まで読んで頂きありがとうございました!!
次回は代表的な確率分布や,連続型確率変数について記載しています.