先日,言語処理100本ノック2020が公開されました.私自身,自然言語処理を初めてから1年しか経っておらず,細かいことはよくわかっていませんが,技術力向上のために全ての問題を解いて公開していこうと思います.
すべてjupyter notebook上で実行するものとし,問題文の制約は都合よく破っていいものとします.
ソースコードはgithubにもあります.あります.
5章はこちら.
環境はPython3.8.2とUbuntu18.04です.
第6章: 機械学習
本章では,Fabio Gasparetti氏が公開しているNews Aggregator Data Setを用い,ニュース記事の見出しを「ビジネス」「科学技術」「エンターテイメント」「健康」のカテゴリに分類するタスク(カテゴリ分類)に取り組む.
必要なデータセットはここからダウンロードしてください.
ダウンロードしたファイルはdata以下に置くものとします.
50. データの入手・整形
News Aggregator Data Setをダウンロードし、以下の要領で学習データ(train.txt),検証データ(valid.txt),評価データ(test.txt)を作成せよ.
1.ダウンロードしたzipファイルを解凍し,readme.txtの説明を読む.
2.情報源(publisher)が”Reuters”, “Huffington Post”, “Businessweek”, “Contactmusic.com”, “Daily Mail”の事例(記事)のみを抽出する.
3.抽出された事例をランダムに並び替える.
4.抽出された事例の80%を学習データ,残りの10%ずつを検証データと評価データに分割し,それぞれtrain.txt,valid.txt,test.txtというファイル名で保存する.ファイルには,1行に1事例を書き出すこととし,カテゴリ名と記事見出しのタブ区切り形式とせよ.
学習データと評価データを作成したら,各カテゴリの事例数を確認せよ.
zipファイルからデータセットを読み込みます.
import zipfile
# zipファイルから読み込む
with zipfile.ZipFile('data/NewsAggregatorDataset.zip') as f:
with f.open('newsCorpora.csv') as g:
data = g.read()
# バイト列をデコード
data = data.decode('UTF-8').splitlines()
# タブ区切り
data = [line.split('\t') for line in data]
len(data)
422937
情報源を指定して,ランダムに並び替えます.
publishers = {
'Reuters',
'Huffington Post',
'Businessweek',
'Contactmusic.com',
'Daily Mail',
}
data = [
lst
for lst in data
if lst[3] in publishers
]
data.sort()
len(data)
13356
カテゴリ名と記事見出し以外を捨てます.
data = [
[lst[4], lst[1]]
for lst in data
]
学習・検証・評価データに分割します.sklearnにも同様の機能の関数がありますが,わざわざブラックボックスに手を出すほど難しいことじゃないです.切り出す場所を指定して切るだけです.
train_end = int(len(data) * 0.8)
valid_end = int(len(data) * 0.9)
train = data[:train_end]
valid = data[train_end:valid_end]
test = data[valid_end:]
print('学習データ', len(train))
print('検証データ', len(valid))
print('評価データ', len(test))
学習データ 10684
検証データ 1336
評価データ 1336
ファイルに保存します.
def write_dataset(filename, data):
with open(filename, 'w') as f:
for lst in data:
print('\t'.join(lst), file = f)
write_dataset('../train.txt', train)
write_dataset('../valid.txt', valid)
write_dataset('../test.txt', test)
カテゴリごとの事例数を確認します.
from collections import Counter
from tabulate import tabulate
categories = ['b', 't', 'e', 'm']
category_names = ['business', 'science and technology', 'entertainment', 'health']
table = [
[name] + [freqs[cat] for cat in categories]
for name, freqs in [
('train', Counter([cat for cat, _ in train])),
('valid', Counter([cat for cat, _ in valid])),
('test', Counter([cat for cat, _ in test])),
]
]
tabulate(table, headers = categories)
b t e m
----- ---- ---- ---- ---
train 4463 1223 4277 721
valid 617 168 459 92
test 547 134 558 97
51. 特徴量抽出
学習データ,検証データ,評価データから特徴量を抽出し,それぞれtrain.feature.txt,valid.feature.txt,test.feature.txtというファイル名で保存せよ(このファイルは後に問題70で再利用する). ファイルには,1行に1事例を書き出すこととし,カテゴリ名と記事見出しのスペース区切り形式とせよ. なお,カテゴリ分類に有用そうな特徴量は各自で自由に設計せよ.記事の見出しを単語列に変換したものが最低限のベースラインとなるであろう.
tf-idfとか単語ベクトルとかしてもよさそうですが,特徴量抽出の闇は無限に深いので,浅瀬に座礁していたいと思います.つまりBag-of-Words.
import re
import spacy
import nltk
単語列に分割して,小文字化と語幹化をします.
nlp = spacy.load('en')
stemmer = nltk.stem.snowball.SnowballStemmer(language='english')
def tokenize(x):
x = re.sub(r'\s+', ' ', x)
x = nlp.make_doc(x) # nlp(x)は遅い tokenizer以外も走るので
x = [stemmer.stem(doc.lemma_.lower()) for doc in x]
return x
tokenized_train = [[cat, tokenize(line)] for cat, line in train]
tokenized_valid = [[cat, tokenize(line)] for cat, line in valid]
tokenized_test = [[cat, tokenize(line)] for cat, line in test]
特徴量として使うトークンを抽出します.
# 出現頻度を数える
counter = Counter([
token
for _, tokens in tokenized_train
for token in tokens
])
# 高頻度・低頻度の語を取り除く
vocab = [
token
for token, freq in counter.most_common()
if 2 < freq < 300
]
len(vocab)
4790
bi-gramも特徴量とします.小文字化でUSもusもおなじになっちゃったわけですが,bi-gramも入れると"us stock"なんかが特徴量として効きます.
bi_grams = Counter([
bi_gram
for _, sent in tokenized_train
for bi_gram in zip(sent, sent[1:])
]).most_common()
bi_grams = [tup for tup, freq in bi_grams if freq > 4]
len(bi_grams)
3094
保存します.
with open('result/vocab_for_news.txt', 'w') as f:
for token in vocab:
print(token, file = f)
with open('result/bi_grams_for_news.txt', 'w') as f:
for tup in bi_grams:
print(' '.join(tup), file = f)
全特徴量
features = vocab + [' '.join(x) for x in bi_grams]
len(features)
7884
特徴量を抽出して保存しておきます.
import numpy as np
vocab_dict = {x:n for n, x in enumerate(vocab)}
bi_gram_dict = {x:n for n, x in enumerate(bi_grams)}
def count_uni_gram(sent):
lst = [0 for token in vocab]
for token in sent:
if token in vocab_dict:
lst[vocab_dict[token]] += 1
return lst
def count_bi_gram(sent):
lst = [0 for token in bi_grams]
for tup in zip(sent, sent[1:]):
if tup in bi_gram_dict:
lst[bi_gram_dict[tup]] += 1
return lst
def prepare_feature_dataset(data):
ts = [categories.index(cat) for cat, _ in data]
xs = [
count_uni_gram(sent) + count_bi_gram(sent)
for _, sent in data
]
return np.array(xs, dtype=np.float32), np.array(ts, dtype=np.int8)
def write_feature_dataset(filename, xs, ts):
with open(filename, 'w') as f:
for t, x in zip(ts, xs):
line = categories[t] + ' ' + ' '.join([str(int(n)) for n in x])
print(line, file = f)
train_x, train_t = prepare_feature_dataset(tokenized_train)
valid_x, valid_t = prepare_feature_dataset(tokenized_valid)
test_x, test_t = prepare_feature_dataset(tokenized_test)
write_feature_dataset('result/train.feature.txt', train_x, train_t)
write_feature_dataset('result/valid.feature.txt', valid_x, valid_t)
write_feature_dataset('result/test.feature.txt', test_x, test_t)
例をみます.
import pandas as pd
with open('result/train.feature.txt') as f:
table = [line.strip().split(' ') for _, line in zip(range(10), f)]
pd.DataFrame(table, columns=['category'] + features)

52. 学習
51で構築した学習データを用いて,ロジスティック回帰モデルを学習せよ.
sklearnを使います.
最急降下法でロジスティック回帰を実装するぐらいなら簡単ですが,準ニュートン法をスクラッチでやろうとするとヘッセ行列で心が打ち砕かれて線形探索あたりで心が折れるため,日頃から精神的負荷を強く抱えている類の人類には到底推奨できません.これは体験談ですが,アルミホイルを転がしてアルミホ条件に合うところで止めるなどの奇行に走る恐れがあります.一方,scikit-learnは寝てても使えます.
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(max_iter=1000)
lr.fit(train_x, train_t)
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, l1_ratio=None, max_iter=1000,
multi_class='auto', n_jobs=None, penalty='l2',
random_state=None, solver='lbfgs', tol=0.0001, verbose=0,
warm_start=False)
モデルを作ってfit()すればいいので,寝ててもできます.とても簡単ですね.
53. 予測
52で学習したロジスティック回帰モデルを用い,与えられた記事見出しからカテゴリとその予測確率を計算するプログラムを実装せよ.
def predict(x):
out = lr.predict_proba(x)
preds = out.argmax(axis=1)
probs = out.max(axis=1)
return preds, probs
訓練データで予測.
preds, probs = predict(train_x)
pd.DataFrame([[y, p] for y, p in zip(preds, probs)], columns = ['予測', '確率'])

評価データで予測.
preds, probs = predict(test_x)
pd.DataFrame([[y, p] for y, p in zip(preds, probs)], columns = ['予測', '確率'])

54. 正解率の計測
52で学習したロジスティック回帰モデルの正解率を,学習データおよび評価データ上で計測せよ.
def accuracy(lr, xs, ts):
ys = lr.predict(xs)
return (ys == ts).mean()
print('訓練データ')
print(accuracy(lr, train_x, train_t))
訓練データ
0.994664919505803
print('評価データ')
print(accuracy(lr, test_x, test_t))
評価データ
0.906437125748503
55. 混同行列の作成
52で学習したロジスティック回帰モデルの混同行列(confusion matrix)を,学習データおよび評価データ上で作成せよ.
seabornを使うとしあわせになります.confusion matrixのcはseabornのseaだと思います.
import seaborn as sns
def confusion_matrix(xs, ts):
num_class = np.unique(ts).size
mat = np.zeros((num_class, num_class), dtype=np.int32)
ys = lr.predict(xs)
for y, t in zip(ys, ts):
mat[t, y] += 1
return mat
def show_cm(cm):
sns.heatmap(cm, annot=True, cmap = 'Blues', xticklabels = categories, yticklabels = categories)
train_cm = confusion_matrix(train_x, train_t)
print('訓練データ')
print(train_cm)
show_cm(train_cm)
訓練データ
[[4451 10 2 0]
[ 25 1192 6 0]
[ 4 1 4271 1]
[ 5 0 3 713]]

test_cm = confusion_matrix(test_x, test_t)
print('評価データ')
print(test_cm)
show_cm(test_cm)
評価データ
[[516 13 12 6]
[ 35 87 10 2]
[ 22 2 531 3]
[ 10 5 5 77]]

56. 適合率,再現率,F1スコアの計測
52で学習したロジスティック回帰モデルの適合率,再現率,F1スコアを,評価データ上で計測せよ.カテゴリごとに適合率,再現率,F1スコアを求め,カテゴリごとの性能をマイクロ平均(micro-average)とマクロ平均(macro-average)で統合せよ.
sklearnにも同様の処理をする関数がありますが,これぐらいは自分で実装すればいいという立場です.
タスクによっては$F_{0.5}$値を使うものもありますし,自分で書けたほうがいいと思っています.
tp = test_cm.diagonal()
tn = test_cm.sum(axis=1) - tp
fp = test_cm.sum(axis=0) - tp
p = tp / (tp + tn)
r = tp / (tp + fp)
F = 2 * p * r / (p + r)
micro_p = tp.sum() / (tp + tn).sum()
micro_r = tp.sum() / (tp + fp).sum()
micro_F = 2 * micro_p * micro_r / (micro_p + micro_r)
micro_ave = np.array([micro_p, micro_r, micro_F])
macro_p = p.mean()
macro_r = r.mean()
macro_F = 2 * macro_p * macro_r / (macro_p + macro_r)
macro_ave = np.array([macro_p, macro_r, macro_F])
table = np.array([p, r, F]).T
table = np.vstack([table, micro_ave, macro_ave])
pd.DataFrame(
table,
index = categories + ['マイクロ平均'] + ['マクロ平均'],
columns = ['再現率', '適合率', 'F1スコア'])

57. 特徴量の重みの確認
52で学習したロジスティック回帰モデルの中で,重みの高い特徴量トップ10と,重みの低い特徴量トップ10を確認せよ.
def show_weight(directional, N):
for i, cat in enumerate(categories):
indices = lr.coef_[i].argsort()[::directional][:N]
best = np.array(features)[indices]
weight = lr.coef_[i][indices]
print(category_names[i])
display(pd.DataFrame([best, weight], index = ['特徴量', '重み'], columns = np.arange(N) + 1))
重みの大きな特徴量トップ10
show_weight(-1, 10)

show_weight(1, 10)

それらしい特徴量が抽出できているように見えます.
58. 正則化パラメータの変更
ロジスティック回帰モデルを学習するとき,正則化パラメータを調整することで,学習時の過学習(overfitting)の度合いを制御できる.異なる正則化パラメータでロジスティック回帰モデルを学習し,学習データ,検証データ,および評価データ上の正解率を求めよ.実験の結果は,正則化パラメータを横軸,正解率を縦軸としたグラフにまとめよ.
import matplotlib.pyplot as plt
import japanize_matplotlib
from tqdm import tqdm
時間がかかるのでtqdm.tqdmで監視します.
Cs = np.arange(0.1, 5.1, 0.1)
lrs = [LogisticRegression(C=C, max_iter=1000).fit(train_x, train_t) for C in tqdm(Cs)]
train_accs = [accuracy(lr, train_x, train_t) for lr in lrs]
valid_accs = [accuracy(lr, valid_x, valid_t) for lr in lrs]
test_accs = [accuracy(lr, test_x, test_t) for lr in lrs]
plt.plot(Cs, train_accs, label = '学習')
plt.plot(Cs, valid_accs, label = '検証')
plt.plot(Cs, test_accs, label = '評価')
plt.legend()
plt.show()

正則化が弱いと過学習していますね.
59. ハイパーパラメータの探索
学習アルゴリズムや学習パラメータを変えながら,カテゴリ分類モデルを学習せよ.評価データ上の正解率が最も高くなる学習アルゴリズム・パラメータを求めよ.
打ち切り誤差を変えてみます.
tols = np.logspace(0, 2, 50)
lrs = [LogisticRegression(tol=tol, max_iter=1000).fit(train_x, train_t) for tol in tqdm(tols)]
train_accs = [accuracy(lr, train_x, train_t) for lr in lrs]
valid_accs = [accuracy(lr, valid_x, valid_t) for lr in lrs]
test_accs = [accuracy(lr, test_x, test_t) for lr in lrs]
plt.plot(tols, train_accs, label = '学習')
plt.plot(tols, valid_accs, label = '検証')
plt.plot(tols, test_accs, label = '評価')
plt.xscale('log')
plt.legend()
plt.show()

ロジスティックス回帰以外も試してみたいと思います.
そこで,sklearnの有名なフローチャートを見てなにかないかなという気持ちをします.
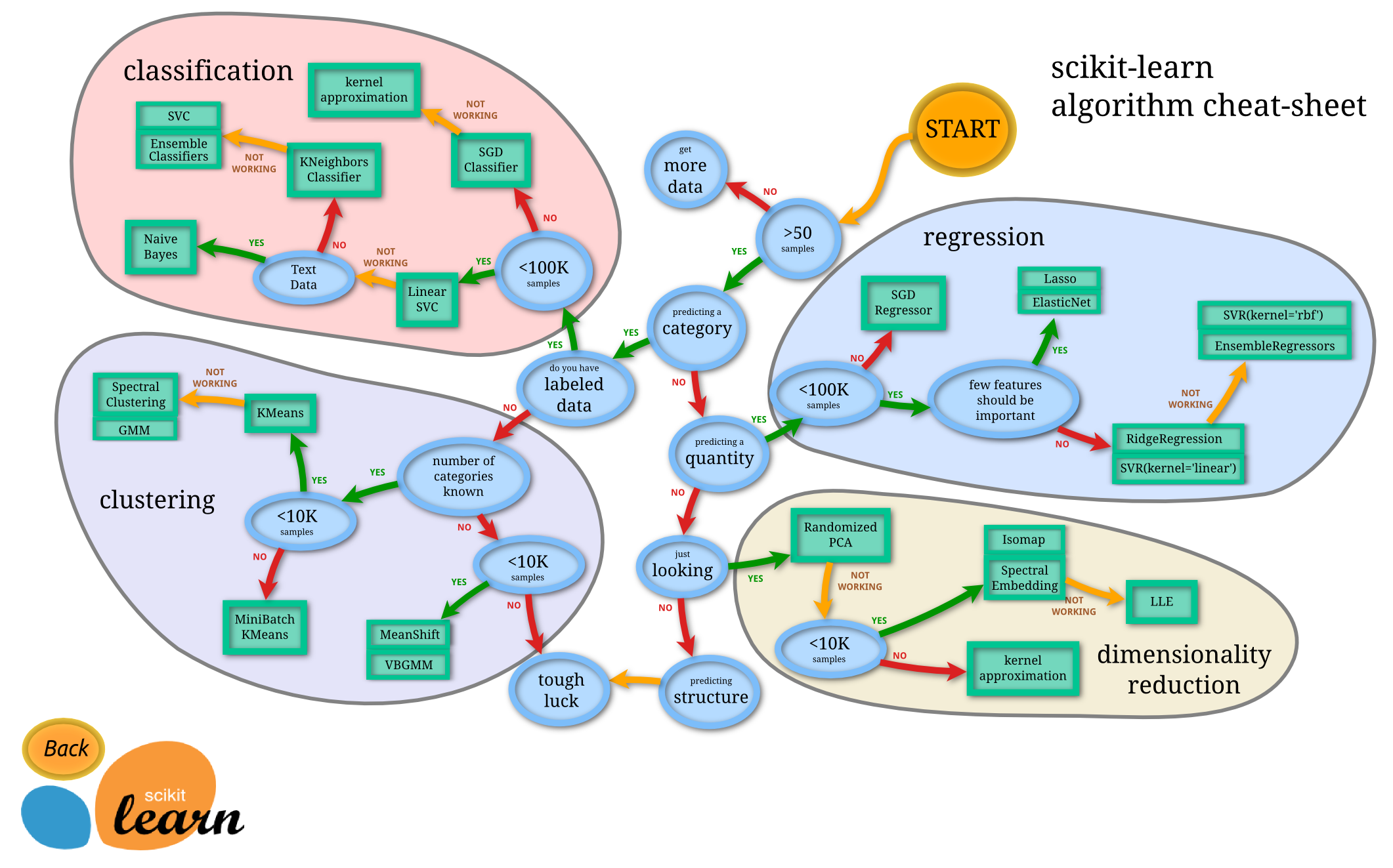
ナイーブベイズ
from sklearn.naive_bayes import MultinomialNB
nb = MultinomialNB()
nb.fit(train_x, train_t)
MultinomialNB(alpha=1.0, class_prior=None, fit_prior=True)
accuracy(nb, train_x, train_t)
0.9429988768251591
accuracy(nb, test_x, test_t)
0.8907185628742516
テキスト分類コスパ最強ナイーブベイズ
線形サポートベクトルマシン
from sklearn.svm import LinearSVC
svc = LinearSVC(C=0.1)
svc.fit(train_x,train_t)
LinearSVC(C=0.1, class_weight=None, dual=True, fit_intercept=True,
intercept_scaling=1, loss='squared_hinge', max_iter=1000,
multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
verbose=0)
accuracy(svc, train_x, train_t)
0.9908274054661176
accuracy(svc, test_x, test_t)
0.9041916167664671
とてもいいですね.