先日,言語処理100本ノック2020が公開されました.私自身,自然言語処理を初めてから1年しか経っておらず,細かいことはよくわかっていませんが,技術力向上のために全ての問題を解いて公開していこうと思います.
すべてjupyter notebook上で実行するものとし,問題文の制約は都合よく破っていいものとします.
ソースコードはgithubにもあります.あります.
6章はこちら.
環境はPython3.8.2とUbuntu18.04です.
第7章: 単語ベクトル
単語の意味を実ベクトルで表現する単語ベクトル(単語埋め込み)に関して,以下の処理を行うプログラムを作成せよ.
必要なデータセットはここからダウンロードしてください.
ダウンロードしたファイルはdata以下に置くものとします.
60. 単語ベクトルの読み込みと表示
Google Newsデータセット(約1,000億単語)での学習済み単語ベクトル(300万単語・フレーズ,300次元)をダウンロードし,”United States”の単語ベクトルを表示せよ.ただし,”United States”は内部的には”United_States”と表現されていることに注意せよ.
gensimを使います.
from gensim.models import KeyedVectors
model = KeyedVectors.load_word2vec_format('data/GoogleNews-vectors-negative300.bin.gz', binary=True)
model["United_States"]
array([-3.61328125e-02, -4.83398438e-02, 2.35351562e-01, 1.74804688e-01,
-1.46484375e-01, -7.42187500e-02, -1.01562500e-01, -7.71484375e-02,
1.09375000e-01, -5.71289062e-02, -1.48437500e-01, -6.00585938e-02,
1.74804688e-01, -7.71484375e-02, 2.58789062e-02, -7.66601562e-02,
-3.80859375e-02, 1.35742188e-01, 3.75976562e-02, -4.19921875e-02,
-3.56445312e-02, 5.34667969e-02, 3.68118286e-04, -1.66992188e-01,
-1.17187500e-01, 1.41601562e-01, -1.69921875e-01, -6.49414062e-02,
-1.66992188e-01, 1.00585938e-01, 1.15722656e-01, -2.18750000e-01,
-9.86328125e-02, -2.56347656e-02, 1.23046875e-01, -3.54003906e-02,
-1.58203125e-01, -1.60156250e-01, 2.94189453e-02, 8.15429688e-02,
6.88476562e-02, 1.87500000e-01, 6.49414062e-02, 1.15234375e-01,
-2.27050781e-02, 3.32031250e-01, -3.27148438e-02, 1.77734375e-01,
-2.08007812e-01, 4.54101562e-02, -1.23901367e-02, 1.19628906e-01,
7.44628906e-03, -9.03320312e-03, 1.14257812e-01, 1.69921875e-01,
-2.38281250e-01, -2.79541016e-02, -1.21093750e-01, 2.47802734e-02,
7.71484375e-02, -2.81982422e-02, -4.71191406e-02, 1.78222656e-02,
-1.23046875e-01, -5.32226562e-02, 2.68554688e-02, -3.11279297e-02,
-5.59082031e-02, -5.00488281e-02, -3.73535156e-02, 1.25976562e-01,
5.61523438e-02, 1.51367188e-01, 4.29687500e-02, -2.08007812e-01,
-4.78515625e-02, 2.78320312e-02, 1.81640625e-01, 2.20703125e-01,
-3.61328125e-02, -8.39843750e-02, -3.69548798e-05, -9.52148438e-02,
-1.25000000e-01, -1.95312500e-01, -1.50390625e-01, -4.15039062e-02,
1.31835938e-01, 1.17675781e-01, 1.91650391e-02, 5.51757812e-02,
-9.42382812e-02, -1.08886719e-01, 7.32421875e-02, -1.15234375e-01,
8.93554688e-02, -1.40625000e-01, 1.45507812e-01, 4.49218750e-02,
-1.10473633e-02, -1.62353516e-02, 4.05883789e-03, 3.75976562e-02,
-6.98242188e-02, -5.46875000e-02, 2.17285156e-02, -9.47265625e-02,
4.24804688e-02, 1.81884766e-02, -1.73339844e-02, 4.63867188e-02,
-1.42578125e-01, 1.99218750e-01, 1.10839844e-01, 2.58789062e-02,
-7.08007812e-02, -5.54199219e-02, 3.45703125e-01, 1.61132812e-01,
-2.44140625e-01, -2.59765625e-01, -9.71679688e-02, 8.00781250e-02,
-8.78906250e-02, -7.22656250e-02, 1.42578125e-01, -8.54492188e-02,
-3.18359375e-01, 8.30078125e-02, 6.34765625e-02, 1.64062500e-01,
-1.92382812e-01, -1.17675781e-01, -5.41992188e-02, -1.56250000e-01,
-1.21582031e-01, -4.95605469e-02, 1.20117188e-01, -3.83300781e-02,
5.51757812e-02, -8.97216797e-03, 4.32128906e-02, 6.93359375e-02,
8.93554688e-02, 2.53906250e-01, 1.65039062e-01, 1.64062500e-01,
-1.41601562e-01, 4.58984375e-02, 1.97265625e-01, -8.98437500e-02,
3.90625000e-02, -1.51367188e-01, -8.60595703e-03, -1.17675781e-01,
-1.97265625e-01, -1.12792969e-01, 1.29882812e-01, 1.96289062e-01,
1.56402588e-03, 3.93066406e-02, 2.17773438e-01, -1.43554688e-01,
6.03027344e-02, -1.35742188e-01, 1.16210938e-01, -1.59912109e-02,
2.79296875e-01, 1.46484375e-01, -1.19628906e-01, 1.76757812e-01,
1.28906250e-01, -1.49414062e-01, 6.93359375e-02, -1.72851562e-01,
9.22851562e-02, 1.33056641e-02, -2.00195312e-01, -9.76562500e-02,
-1.65039062e-01, -2.46093750e-01, -2.35595703e-02, -2.11914062e-01,
1.84570312e-01, -1.85546875e-02, 2.16796875e-01, 5.05371094e-02,
2.02636719e-02, 4.25781250e-01, 1.28906250e-01, -2.77099609e-02,
1.29882812e-01, -1.15722656e-01, -2.05078125e-02, 1.49414062e-01,
7.81250000e-03, -2.05078125e-01, -8.05664062e-02, -2.67578125e-01,
-2.29492188e-02, -8.20312500e-02, 8.64257812e-02, 7.61718750e-02,
-3.66210938e-02, 5.22460938e-02, -1.22070312e-01, -1.44042969e-02,
-2.69531250e-01, 8.44726562e-02, -2.52685547e-02, -2.96630859e-02,
-1.68945312e-01, 1.93359375e-01, -1.08398438e-01, 1.94091797e-02,
-1.80664062e-01, 1.93359375e-01, -7.08007812e-02, 5.85937500e-02,
-1.01562500e-01, -1.31835938e-01, 7.51953125e-02, -7.66601562e-02,
3.37219238e-03, -8.59375000e-02, 1.25000000e-01, 2.92968750e-02,
1.70898438e-01, -9.37500000e-02, -1.09375000e-01, -2.50244141e-02,
2.11914062e-01, -4.44335938e-02, 6.12792969e-02, 2.62451172e-02,
-1.77734375e-01, 1.23046875e-01, -7.42187500e-02, -1.67968750e-01,
-1.08886719e-01, -9.04083252e-04, -7.37304688e-02, 5.49316406e-02,
6.03027344e-02, 8.39843750e-02, 9.17968750e-02, -1.32812500e-01,
1.22070312e-01, -8.78906250e-03, 1.19140625e-01, -1.94335938e-01,
-6.64062500e-02, -2.07031250e-01, 7.37304688e-02, 8.93554688e-02,
1.81884766e-02, -1.20605469e-01, -2.61230469e-02, 2.67333984e-02,
7.76367188e-02, -8.30078125e-02, 6.78710938e-02, -3.54003906e-02,
3.10546875e-01, -2.42919922e-02, -1.41601562e-01, -2.08007812e-01,
-4.57763672e-03, -6.54296875e-02, -4.95605469e-02, 2.22656250e-01,
1.53320312e-01, -1.38671875e-01, -5.24902344e-02, 4.24804688e-02,
-2.38281250e-01, 1.56250000e-01, 5.83648682e-04, -1.20605469e-01,
-9.22851562e-02, -4.44335938e-02, 3.61328125e-02, -1.86767578e-02,
-8.25195312e-02, -8.25195312e-02, -4.05273438e-02, 1.19018555e-02,
1.69921875e-01, -2.80761719e-02, 3.03649902e-03, 9.32617188e-02,
-8.49609375e-02, 1.57470703e-02, 7.03125000e-02, 1.62353516e-02,
-2.27050781e-02, 3.51562500e-02, 2.47070312e-01, -2.67333984e-02],
dtype=float32)
61. 単語の類似度
“United States”と”U.S.”のコサイン類似度を計算せよ.
model.similarity("United_States", "U.S.")
0.73107743
62. 類似度の高い単語10件
“United States”とコサイン類似度が高い10語と,その類似度を出力せよ.
import numpy as np
import pandas as pd
simularities = model.most_similar("United_States")
pd.DataFrame(
simularities,
columns = ['単語', '類似度'],
index = np.arange(len(simularities)) + 1
)

63. 加法構成性によるアナロジー
“Spain”の単語ベクトルから”Madrid”のベクトルを引き,”Athens”のベクトルを足したベクトルを計算し,そのベクトルと類似度の高い10語とその類似度を出力せよ.
simularities = model.most_similar(positive=['Spain', 'Athens'], negative=['Madrid'])
pd.DataFrame(
simularities,
columns = ['単語', '類似度'],
index = np.arange(len(simularities)) + 1
)

64. アナロジーデータでの実験
単語アナロジーの評価データをダウンロードし,vec(2列目の単語) - vec(1列目の単語) + vec(3列目の単語)を計算し,そのベクトルと類似度が最も高い単語と,その類似度を求めよ.求めた単語と類似度は,各事例の末尾に追記せよ.
with open('data/questions-words.txt') as f:
lines = f.read().splitlines()
dataset = []
category = None
for line in lines:
if line.startswith(':'):
category = line[2:]
else:
lst = [category] + line.split(' ')
dataset.append(lst)
pd.DataFrame(dataset[:10])

from tqdm import tqdm
for i, lst in enumerate(tqdm(dataset)):
pred, prob = model.most_similar(positive = lst[2:4], negative = lst[1:2], topn = 1)[0]
dataset[i].append(pred)
pd.DataFrame(dataset[:10])
65. アナロジータスクでの正解率
64の実行結果を用い,意味的アナロジー(semantic analogy)と文法的アナロジー(syntactic analogy)の正解率を測定せよ.
evaluate_word_analogies()使えばいいっていう説は広く知られています.
semantic_analogy = [lst[-2:] for lst in dataset if not lst[0].startswith('gram')]
syntactic_analogy = [lst[-2:] for lst in dataset if lst[0].startswith('gram')]
acc = np.mean([true == pred for true, pred in semantic_analogy])
print('意味的アナロジー 正解率:', acc)
意味的アナロジー 正解率: 0.7308602999210734
acc = np.mean([true == pred for true, pred in syntactic_analogy])
print('文法的アナロジー 正解率:', acc)
文法的アナロジー 正解率: 0.7400468384074942
66. WordSimilarity-353での評価
The WordSimilarity-353 Test Collectionの評価データをダウンロードし,単語ベクトルにより計算される類似度のランキングと,人間の類似度判定のランキングの間のスピアマン相関係数を計算せよ.
import zipfile
# zipファイルから読み込む
with zipfile.ZipFile('data/wordsim353.zip') as f:
with f.open('combined.csv') as g:
data = g.read()
# バイト列をデコード
data = data.decode('UTF-8').splitlines()
data = data[1:]
# タブ区切り
data = [line.split(',') for line in data]
len(data)
353
for i, lst in enumerate(data):
sim = model.similarity(lst[0], lst[1])
data[i].append(sim)
pd.DataFrame(
data[:10],
columns = ['単語1', '単語2', '人間', 'ベクトル']
)

from scipy.stats import spearmanr
順位を取り出すにはargsortを2回適用するというのもあるけど,計算量的には無駄かもしれない
def rank(x):
args = np.argsort(-np.array(x))
rank = np.empty_like(args)
rank[args] = np.arange(len(x))
return rank
human = [float(lst[2]) for lst in data]
w2v = [lst[3] for lst in data]
human_rank = rank(human)
w2v_rank = rank(w2v)
rho, p_value = spearmanr(human_rank, w2v_rank)
順位相関係数 : 0.700313895424209
p値 : 2.4846350292113526e-53
print('順位相関係数 :', rho)
print('p値 :', p_value)
import matplotlib.pyplot as plt
plt.scatter(human_rank, w2v_rank)
plt.show()

67. k-meansクラスタリング
国名に関する単語ベクトルを抽出し,k-meansクラスタリングをクラスタ数k=5として実行せよ.
国名をどこからとってくるのがいいのかよくわからないが,アナロジーのデータセットでいいやってなる
countries = {
country
for lst in dataset
for country in [lst[2], lst[4]]
if lst[0] in {'capital-common-countries', 'capital-world'}
} | {
country
for lst in dataset
for country in [lst[1], lst[3]]
if lst[0] in {'currency', 'gram6-nationality-adjective'}
}
countries = list(countries)
len(countries)
129
country_vectors = [model[country] for country in countries]
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=5)
kmeans.fit(country_vectors)
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
n_clusters=5, n_init=10, n_jobs=None, precompute_distances='auto',
random_state=None, tol=0.0001, verbose=0)
for i in range(5):
cluster = np.where(kmeans.labels_ == i)[0]
print('クラス', i)
print(', '.join([countries[k] for k in cluster]))
クラス 0
Suriname, Honduras, Tuvalu, Guyana, Venezuela, Peru, Cuba, Ecuador, Nicaragua, Dominica, Colombia, Belize, Mexico, Bahamas, Jamaica, Chile
クラス 1
Netherlands, Egypt, France, Syria, Finland, Germany, Uruguay, Switzerland, Greenland, Italy, Lebanon, Malta, Algeria, Europe, Tunisia, Brazil, Ireland, England, Libya, Spain, Argentina, Liechtenstein, Iran, Jordan, USA, Iceland, Sweden, Norway, Qatar, Portugal, Denmark, Canada, Israel, Belgium, Morocco, Austria
クラス 2
Kazakhstan, Lithuania, Turkmenistan, Serbia, Croatia, Greece, Uzbekistan, Armenia, Latvia, Albania, Slovenia, Cyprus, Ukraine, Georgia, Belarus, Bulgaria, Kyrgyzstan, Macedonia, Estonia, Montenegro, Turkey, Azerbaijan, Tajikistan, Poland, Russia, Romania, Hungary, Slovakia, Moldova
クラス 3
Ghana, Senegal, Zambia, Sudan, Somalia, Zimbabwe, Gabon, Madagascar, Angola, Liberia, Gambia, Niger, Uganda, Mauritania, Namibia, Eritrea, Botswana, Malawi, Mozambique, Guinea, Kenya, Nigeria, Burundi, Mali, Rwanda
クラス 4
Japan, China, Pakistan, Samoa, Bahrain, Fiji, Australia, India, Laos, Bhutan, Malaysia, Taiwan, Cambodia, Nepal, Korea, Oman, Thailand, Bangladesh, Indonesia, Iraq, Vietnam, Afghanistan, Philippines
それらしくわかれています.
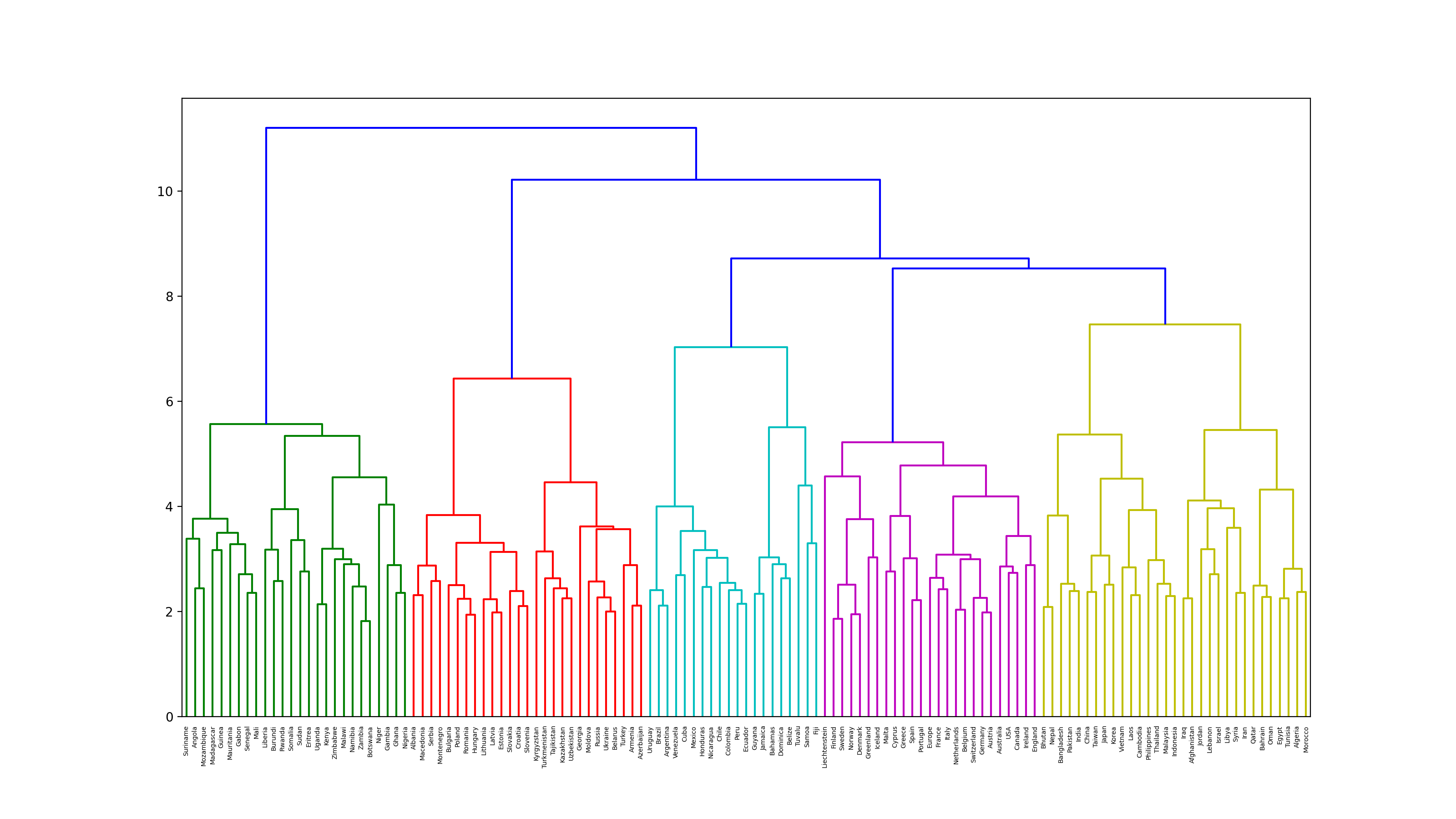
68. Ward法によるクラスタリング
国名に関する単語ベクトルに対し,Ward法による階層型クラスタリングを実行せよ.さらに,クラスタリング結果をデンドログラムとして可視化せよ.
from scipy.cluster.hierarchy import dendrogram, linkage
plt.figure(figsize=(16, 9), dpi=200)
Z = linkage(country_vectors, method='ward')
dendrogram(Z, labels = countries)
plt.show()
69. t-SNEによる可視化
国名に関する単語ベクトルのベクトル空間をt-SNEで可視化せよ.
from sklearn.manifold import TSNE
tsne = TSNE()
tsne.fit(country_vectors)
TSNE(angle=0.5, early_exaggeration=12.0, init='random', learning_rate=200.0,
method='barnes_hut', metric='euclidean', min_grad_norm=1e-07,
n_components=2, n_iter=1000, n_iter_without_progress=300, n_jobs=None,
perplexity=30.0, random_state=None, verbose=0)
plt.figure(figsize=(15, 15), dpi=300)
plt.scatter(tsne.embedding_[:, 0], tsne.embedding_[:, 1])
for (x, y), name in zip(tsne.embedding_, countries):
plt.annotate(name, (x, y))
plt.show()
