TensorFlow関連の記事でニューラルネットやDeep Learning以外の使用例が少なかったので、その一例として非負値行列分解(NMF)を実装してみました。
開発環境
OS: Ubuntu 14.04
CPU: Core i7-3770 3.40GHz×8
メモリ: 16GB
TersorFlow: ver.0.6.0 CPUモード
Python version: 2.7
非負値行列分解(Non-negative Matrix Factorization)
NMFは非負値行列Vを2つの非負値行列H,Wの積で近似するアルゴリズムです。
特徴抽出、次元削減、クラスタリング手法として画像処理、自然言語など幅広い分野で用いられています。
問題設定
入力:$V \in \mathcal{R}^{m \times n} _{+},\ r \in \mathcal{N}^+$
出力:$\underset{W,H} {\arg\min} ||V-WH||_{F}^{2}\ \ s.t.\ W \in \mathcal{R} _{+} ^{m \times r}, H \in \mathcal{R} _{+} ^ {r \times n} $
アルゴリズム
今回はNMFの最適化として最も実装が簡単な乗法的更新アルゴリズム(Multiplicative update rule)を使います。
MUアルゴリズムでは以下の更新式を収束するまで交互に実行します。
H_{a\mu} \leftarrow H_{a\mu}\frac{(W^TV)_{a\mu}}{(W^TWH)_{a\mu}},\ \
W_{ia} \leftarrow W_{ia}\frac{(VH^T)_{ia}}{(WHH^T)_{ia}}
参考リンク: Algorithms for Non-negative Matrix Factorization
実装
クラス本体は以下のように実装しました。
# -*- coding: utf-8 -*-
from __future__ import division
import numpy as np
import tensorflow as tf
class TFNMF(object):
"""Non-negative Matrix Factorization by TensorFlow"""
def __init__(self, V, rank):
#Numpy行列からTensorFlowのTensorに変換
V_ = tf.constant(V, dtype=tf.float32)
shape = V.shape
#平均 sqrt(V.mean() / rank) の一様乱数にスケール
scale = 2 * np.sqrt(V.mean() / rank)
initializer = tf.random_uniform_initializer(maxval=scale)
#行列H,Wの変数生成
self.H = H = tf.get_variable("H", [rank, shape[1]],
initializer=initializer)
self.W = W = tf.get_variable(name="W", shape=[shape[0], rank],
initializer=initializer)
#収束判定のためにWを保存する
W_old = tf.get_variable(name="W_old", shape=[shape[0], rank])
self._save_W = W_old.assign(W)
#MUアルゴリズム
#Hを更新する
Wt = tf.transpose(W)
WV = tf.matmul(Wt, V_)
WWH = tf.matmul(tf.matmul(Wt, W), H)
WV_WWH = WV / WWH
with tf.device('/cpu:0'):
#0割りでnanが入った要素を0に変換する
WV_WWH = tf.select(tf.is_nan(WV_WWH),
tf.zeros_like(WV_WWH),
WV_WWH)
H_new = H * WV_WWH
self._update_H = H.assign(H_new)
#Wを更新する(Hは更新済み)
Ht = tf.transpose(H)
VH = tf.matmul(V_, Ht)
WHH = tf.matmul(W, tf.matmul(H, Ht))
VH_WHH = VH / WHH
with tf.device('/cpu:0'):
#0割りでnanが入った要素を0に変換する
WV_WWH = tf.select(tf.is_nan(WV_WWH),
tf.zeros_like(WV_WWH),
WV_WWH)
W_new = W * VH_WHH
self._update_W = W.assign(W_new)
#Wの各要素の変化総量
self._delta = tf.reduce_sum(tf.abs(W_old - W))
def run(self, sess, max_iter=200):
tf.initialize_all_variables().run()
for i in range(max_iter):
sess.run(self._save_W)
H, _ = sess.run([self.H, self._update_H])
W, _ = sess.run([self.W, self._update_W])
delta = sess.run(self._delta)
if delta < 0.001:
break
return W, H
実行時間
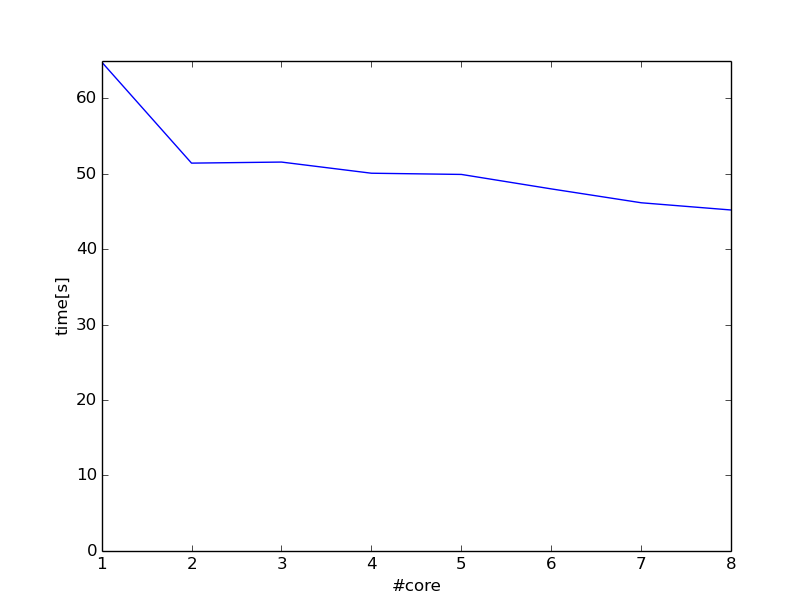
CPUの使用コア数を変えて実行時間を計測します。
入力は10000×10000ランダム行列、ランク数は10としました。
実行スクリプトは以下の通りです。
# -*- coding: utf-8 -*-
from __future__ import print_function
import time
import numpy as np
import tensorflow as tf
from tfnmf import TFNMF
def main():
V = np.random.rand(10000,10000)
rank = 10
num_core = 8
tfnmf = TFNMF(V, rank)
config = tf.ConfigProto(inter_op_parallelism_threads=num_core,
intra_op_parallelism_threads=num_core)
with tf.Session(config=config) as sess:
start = time.time()
W, H = tfnmf.run(sess)
print("Computational Time: ", time.time() - start)
#2乗誤差計算
W = np.mat(W)
H = np.mat(H)
error = np.power(V - W * H, 2).sum()
print("Reconstruction Error: ", error)
if __name__ == '__main__':
main()
コア数8で実行した時の結果です。Reconstruction Errorは目的関数である2乗誤差を表しています。
$python main.py
I tensorflow/core/common_runtime/local_device.cc:40] Local device intra op parallelism threads: 8
I tensorflow/core/common_runtime/direct_session.cc:58] Direct session inter op parallelism threads: 8
Computational Time: 45.2025268078
Reconstruction Error: 8321195.31013
1コアに比べて8コアは約1.4倍高速になりました。
思っていたよりオーバーヘッドが大きくコア数を増やしても実行時間が激的には速くなりませんでした。
W,Hの更新のたびにsess.run()するのはあまり効率の良い方法ではないのかもしれません。
おわりに
今回はTensorFlowを行列演算にしか使っていないので役不足感がありましたが、並列計算を簡単に記述できるのは素晴らしいですね。
次回はテンソル分解を実装してみようと思います。