はじめに
- 自己紹介:UbuntuでPythonを書いてデータ分析とか異常検知してます。
- Twitterやってます。
- AutoMLの一つであるNAS(Neural Architecture Search)に興味があります。
- NAS(Neural architecture search)のベンチマークであるNAS-BENCH-1SHOT1(Elsken et al. 2019)を翻訳&解説しました。
- リンクはこちら
- イイネと思ったらぜひフォロー, thumbs-up&拡散をお願いします!
目次
- イントロ
- 探索空間(search space)
- 探索戦略(search strategy)
- パフォーマンス推定(performance estimation strategy)
- 今後の展望(Future Directions)
イントロ
NAS(Neural architecture search)はAutoML(Hutter 2019) のサブフィールドで、NN(ニューラルネット)の構造を自動的に最適化する手法のことです。
NASによって生み出されたNNは、画像分類(Zoph et al., 2018), (Real et al., 2019)、物体検出(Zoph et al., 2018)、セマンティックセグメンテーション(Chen et al., 2018)などの分野で、人間が設計したNNの性能を上回っています。
NASのポイントは、大きく分けると以下の3つです。
・探索空間はどこか(search space)
要するに、「評価したい構造の集合は何か」みたいなものです。
事前知識を反映させることで探索空間を狭めれば探索コストは減りますが、人間の持つバイアスを超えた新しい構造の発見を妨げてしまうことに繋がります。
・探索戦略は何か(search strategy)
要するに、「探索空間の中をどうやって探索するか」ということです。
広い探索空間で全探索をすると組み合わせ爆発が起こり、探索コストも指数関数的に爆発してしまいます。
かといって、限られた空間しか探索しないと、最適解を見つけられなくなります。
また、現在の知識の元で期待収益が最大の行動を取り続けるか、あるいはより期待収益の高い行動を求めて探索をするか、
というトレードオフの問題も考えなえればいけません。(これをexploration-exploitation trade-offといいます)
・どうやってパフォーマンスを推定するか(performance estimation strategy)
要するに「どうやって未知のデータに対するパフォーマンスを推定するか」ということです。
一般的な「testデータとvalidationデータを分割する」という手法では計算コストがかかり過ぎてしまうので、どうやってコストを削減するかという研究が進んでいます。
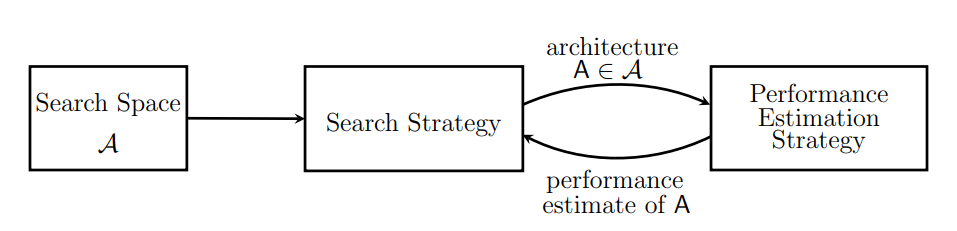
Figure1 : NASの概観図
探索空間(構造の集合)Aの中から探索戦略が一つの構造Aを選び、そのパフォーマンスを推定します。
その推定値に依って、別の構造をAの中から選ぶ…ということを繰り返し、NNの構造を最適化します。
探索空間(search space)
まず、「どんな構造の集合の中からベストなものを選ぶか?」という集合を定義します。
Figure2図中左は、レイヤの列として描かれたシンプルな直列のNNです。
レイヤ$L_i$ は$L_{i-1}$から入力を受け取ります。$L_{i}$の出力は$L_{i+1}$へ渡されます。
このときNNの構造Aは、$A = L_{n} ◦ … ◦L_{1} ◦ L_{0}$ と表すことができます。
この時、探索空間のパラメータは以下の3つです。
(訳者注:まず、図のような直列のNNのみ考えます。分岐やskip connectは一旦考えません)
・レイヤ数の最大値
あくまで最大値であり、レイヤ数が少なくなる可能性もあります。
・レイヤの種類
例えば以下のようなものがあります。
- 全結合層
- 畳み込み層
- プーリング層
- Depthwise Separable Convolutions(Chollet, 2016)
- Dilated Convolutions(Yuand Koltun, 2016)
Depthwise Separable ConvolutionsはN枚の画像からN枚の画像へ(1対1の)畳み込みを行い、その後M枚の画像へ1x1畳み込みを行うことで計算量を削減するテクニックです。
言葉だと説明しにくいですが、こちらの日本語の説明が非常にわかりやすいです。
Dilated Convolutionsはフィルターの中で間引きをすることで計算量を削減する手法です。
こちらや、こちらの資料がわかりやすいです。
・レイヤの種類に応じたハイパーパラメータ
畳み込み層のフィルター数/サイズ/ストライド、全結合層のユニット数(Mendoza et al., 2016)などを決めます。
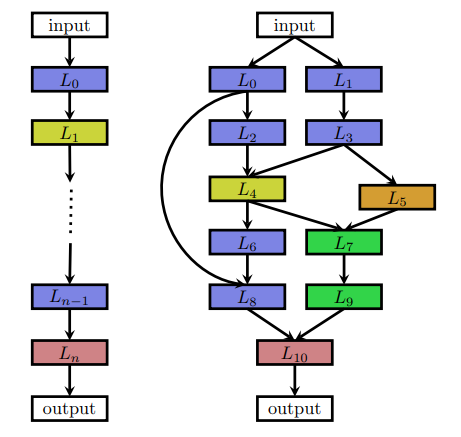
Figure2 : NNのイラスト
シンプルな直列NN(左)と、複雑なNN(右)を図示したもの。
レイヤの種類は色で分けられています。
図中右のNNには、Skip connectionのようなモダンな構造が取り入れられています。
最近のNAS(Brock et al., 2017)(Elsken et al., 2017)(Zoph et al., 2018)(Elsken et al., 2019)(Real et al., 2019)(Cai et al., 2018b) では、skip connectionのような複雑な要素を組み込み、Figure2中右のNNのような複雑な構造を生成することもできます。
この場合、レイヤ$L_{i}$への入力は、それ以前のレイヤの出力の関数$g(L_{i-1}^{out},...,L_{1}^{out},L_{0}^{out})$と表すことができ、大幅に自由度が上がります。
このようなMulti-branch構造には特殊なケースが3つあります。
・シンプルな直列NN
さきほど取り上げた、Figure2(Left)のように表す事ができるNNです。
$g_{i} = L_{i-1}^{out}$が成立します。
・Residual Networks(He et al., 2016)
おなじみのResNetです。
$g_{i} = L_{i-1}^{out}+L_{j}^{out}, j<i-1$が成立します。
・DenseNets(Huang et al., 2017)
おなじみのDenseNetです。
$g_{i} = concat(L_{i-1}^{out},...,L_{1}^{out},L_{0}^{out})$が成立します。
ResNetの式における+(sum)とは、特徴マップの値をそのまま加算するという意味です。
縦5・横5・3チャンネルの特徴マップ同士をsumすると縦5・横5・3チャンネルの特徴マップになります。
一方、DenseNetにおけるconcatenateとは、チャンネル方向に結合するという意味です。
縦5・横5・3チャンネルの特徴マップ同士をconcat()すると縦5・横5・6チャンネルの特徴マップになります。
こちらのアニメーションが非常にわかりやすいです。
さらに、Zoph et al. 2018、Zhong et al. 2018aはNN全体ではなく、繰り返し現れるCell(またはBlock)と呼ばれる単位構造を最適化し、それを積み重ねて全体のNNを構成することを提案しました。
Zoph et al. 2018はNormal CellとReduction Cellという2種類のCellを最適化しました。
Normal Cellはinputの次元を保持し、Reduction Cellは次元を削減します。
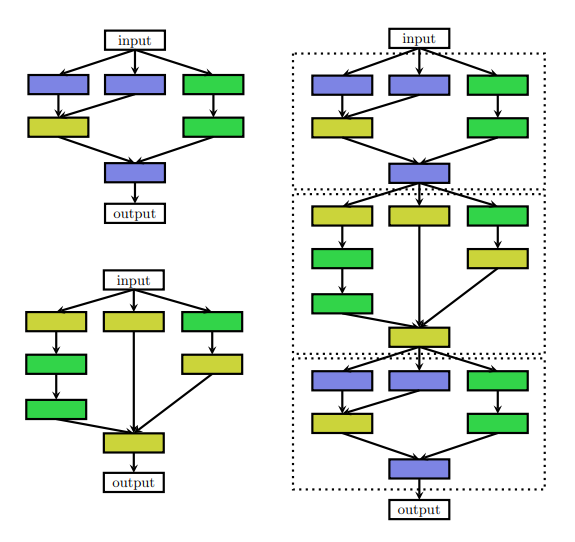
Figure3 : CellからなるNNのイラスト
Normal Cell(左上)、Reduction Cell(左下)、CellからなるNN(右)を図示したもの。
レイヤの種類は色で分けられています。
Cellを用いた手法には3つのメリットがあります。
・探索空間のサイズが大幅に削減できる
Zoph et al., 2018は、Zoph and Le, 2017と比較して7倍以上高速になりました。
これはいわゆるNASNetです。こちらの解説記事が大変わかりやすいです。
7倍以上高速になったとはいっても、計算コストとCIFAR-10のError rateを比較すると、前者は500GPU4daysで2.4%、後者は800GPU21〜28daysで3.6%なので、この時点ではまだまだ計算コストが高いです。(7倍と言う数字はGPUの違いを差っ引いてZophらが推定したものです。前者はNvidia K40、後者はNVidia P100を使用しています。)
2019年現在の低計算コストなNASを挙げると、ENAS(Pham et al., 2018)は1GPU0.45dayで2.89%、ASNG-NAS(Akimoto et al., 2019)は1GPU0.11dayで2.83(±0.14)%を達成しており、実用的なレベルまで計算コストが下がっています。
・他のデータセットに対するモデルの適合が楽
NNのセル数・フィルタ数を変えることで、他のデータセットにも簡単に転用することができます。
Zoph et al., 2018では、CIFAR-10で最適化したNNをImageNetに転用し、SOTAを達成しています。
・Cellの積層構造は有用だと一般的に証明されている
例えばLSTM blockやResidual blockを積層して構成したNNは高い性能を出すことが知られています。
以上の理由から、このCellベースの探索は近年の研究においてよく採用されています。(Real et al., 2019), (Liu et al., 2018a), (Pham et al., 2018), (Elsken et al., 2019), (Cai et al., 2018b), (Liu et al., 2019b), (Zhong et al., 2018b)
しかし、Cellベースの探索では「いくつのCellが、どのように繋がって全体のNNを構成するか」を決める必要があります。(これをMacro-architectureと言います)
Zoph et al., 2018では直列なモデルが採用され、Cai et al. (2018)ではDenseNetのような構造が採用されています。
基本的にNN内でCellは自由に組み合わせる事ができます。
Macro-architecture(NN内のCellの組み合わせ)とMicro-architecture(Cellそのものの構造)を同時に最適化するのが理想です。
Macro-architectureの最適化の手法としてHierarchical Representations(Liu et al., 2018) があります。
これはいくつかのレベルの繰り返し構造(motif)からなります。
1stレベルはプリミティブな操作の集合、2ndレベルはDAG(有向非巡回グラフ)で表される、接続された1stレベルの集合、3rdレベルは同様に接続された2ndレベルの集合、という感じです。
最適空間の広さに依って最適化の難しさは大きく変わります。
Macro-architectureが固定かつCellが1種類だとしても、最適化問題は不連続だし、比較的高次元です。
ここで、多くの構造は固定長のベクトルとして記述できることに注意して下さい。例えばZoph et al., 2018のNormal CellとReduction Cellはカテゴリカル変数を持つ40次元のベクトルの形で表すことができます。
各Cellはそれぞれ5つのブロックで構成され、各ブロックに対して2つの入力の可能性があり、各入力に対して2種類の操作の可能性があるので、252*2 = 40次元の表現になります。
探索戦略(search strategy)
本セクションでは、探索空間からどのように構造を選択するかという戦略を紹介します。
ランダムサーチ、ベイズ最適化、進化的アルゴ、強化学習、勾配ベースなど様々な手法が考えられます。
古くは進化的アルゴがよく採用されていました。(Angeline et al., 1994), (Stanley and Miikkulainen, 2002), (Floreano et al., 2008), (Stanley et al., 2009), (Jozefowicz et al., 2015)
Yao (1999)は、2000年以前にサーベイを発表しています。
ベイズ最適化は2013年の発表以降、初期のNASに大きく貢献しました。(Bergstra et al., 2013), (Domhan et al., 2015), (Mendoza et al., 2016)
強化学習を用いたZoph and Le (2017)がCIFAR-10とPenn Treebankで競争力のあるパフォーマンスを発揮し、NASは機械学習コミニュティの中でホットな研究トピックになりました。しかし、上で述べたように膨大な計算コストがかかりました(800台のGPUで21〜28日)。計算コストを低減するために、様々な研究が進められています。
NASは、以下のようにして強化学習の枠組みで考える事ができます。(Baker et al., 2017), (Zhong et al., 2018), (Zoph et al., 2018)
・エージェントの行動によってNNが生成される
・行動空間が探索空間と対応する
・未知のデータに対するNNのパフォーマンスを報酬にする
方策をどう定め、どう最適化するかは研究によって異なります。
Zoph and Le (2017)はNNの構造を表す文字列を生成するRNNを用いました。
当該の論文ではPolicy gradient法(Williams, 1992)を用いましたが、翌年のZoph et al., 2018ではProximal Policy最適化(Schulman et al., 2017)を採用しています。
Baker et al., 2017はQ学習を用いています。
これらのアプローチは、以下のような逐次決定過程とみなすこともできます。
・方策に基づいて行動を選択し、NNの構造を逐次的に生成する
・環境の"状態"はこれまで選ばれた行動のサマリを含んでいる
・報酬は最後の行動の後に発生する
つまり、statelessな多腕バンディット問題に落とし込めることを意味しています。
関連して、Cai et al., 2018はNASを逐次決定過程の枠組みで考えています。彼らのアプローチでは、以下のように考えます。
状態 : 現在のNNの構造
報酬 : 現在のNNのフォーマンス
行動 : NNの構造の変化(network morphism)

Figure4 : Network morphismのイラスト
Network morphismとは、Parent networkの事前知識を継承したChild networkが生成されること。AC間の変化はdepth morphing、ノードrの変化はwidth and kernel size morphing、CD間の変化はsubnet morphingといいます。
複雑なNetwork morphingも、上記の単純なmorphingの組み合わせによって表現できます。(Chen et al., 2016), (Wei et al., 2017)
可変長のNN構造を取り扱う為に、双方向LSTMを用いて固定長表現に変換しています。
この固定長の表現に基づいて、actor networksが行動を選択します。
これら2つの組み合わせがpolicyを構成し、policyは勾配策定法によって学習されます。
なお、この手法では同じ構造を2度探索することはありません。
続いて、**進化的アルゴ(EA)**について解説します。
EAは生物の進化に着想を得たアルゴリズムの総称です。
その例として、遺伝的アルゴ(GA)、遺伝的プログラミング、進化戦略(ES)、進化的プログラミングなどのアルゴリズムがあります。
EAを初めてNNの設計に用いたのはMiller et al., 1989で、GAを用いて構造を決定し、誤差逆伝播法によって重みを最適化しています。
以降、多くのEA手法(Angeline et al., 1994), (Stanley and Miikkulainen, 2002), (Stanley et al., 2009)では、GAを用いて構造と重みを最適化しています。
しかし、現代のNNは数百万もの重みを持つため、勾配ベースの手法の方がEAよりも適しています。
現代のEA手法(Real et al., 2017; Suganuma et al., 2017; Liu et al., 2018b; Real et al., 2019; Miikkulainen
et al., 2017; Xie and Yuille, 2017; Elsken et al., 2019)でも、重みは勾配ベースで最適化し、NNの構造はEAで最適化するというものが主流です。
最近の研究では勾配の推定値の分散が高い場合は、重みが数百万個あってもEAが勾配ベースに競争力を持つ事が示されています。
例えば強化学習では勾配の推定値の分散が高くなります。
(Salimans et al., 2017), (Such et al., 2017), (Chrabaszcz et al., 2018)
EAはモデルの母集団を進化させ、 全てのevolution stepにおいて最低1つのモデルが母集団からParent networkとしてサンプルされます。そして変異を起こし新しいChild networkを生成します。
NASの文脈においてNetwork morphismとは、
・レイヤの追加/除去
・レイヤのハイパーパラメータの変更
・skip connectionの追加
・学習のハイパーパラメータの変更
といった、ローカルな操作の変化のことを指します。
Child networkの学習後、そのvalidationデータにおけるパフォーマンスが評価され、母集団に追加されます。
EAの各手法は、
・Parent networkをどうサンプルするか
・母集団をどう更新するか
・Child networkをどう生成するか
という点で違いがあります。
たとえば、Real et al. (2017), Real et al. (2019), and Liu et al.(2018b) はtournament selection (Goldberg and Deb, 1991) を用いてParent networkをサンプルしていますが、Elsken et al. (2019)はinverse densityを用いて、多目的パレートフロントからParent networkをサンプルしています。
パレートフロントとは : 多目的最適化の場合、一般的に最適解は1つに定まりません。この時、GAでの多目的最適化で最終世代の個体の適応度(目的関数)プロットした曲線をパレートフロントといいます。目的関数がパレートライン上に乗る時、パレート最適解であると言います。出典
Real et al. (2017)では、最悪の個体を除去する手法が使われています。一方Real et al., 2019では、古い個体を削除することが有益であるとわかりました(greedinessが減少するため)。
Liu et al. (2018b)は個体の除去を行いませんでした。
Child networkを生成する為に、ランダムに初期化するアプローチがほとんどです。
しかしElsken et al. (2019)はLamarckian inheritanceを採用しました。これにより、学習した重みはNetwork morphismを用いてParent networkからChild networkへ渡されます。
Real et al. (2017)はChild networkが(変異の影響を受けないものも含めて)全てのパラメータをParent networkから継承する手法も提案しました。厳密にfunction-preservingではなくとも、ランダム初期化より学習スピードが速くなりました。
更に彼らは学習率を変異させる手法も提案しました。(つまりNASの実行中にlrを最適化するということです)
これらEAの詳細は、Stanley et al., 2019を参照しました。
Real et al. (2019)では強化学習(RL)、EA、ランダムサーチ(RS)の比較を行い、RLとEAは最終的なtest accuracyは同程度だったが、実験中はEAの方がパフォーマンスが良く、小さいモデルを見つけることができた、と述べています。
RLとEA両方ともRSより良い性能でしたが、差は小さかったようです。CIFAR-10のtest errorで比較すると、RSは4%、RLとEAは3.5%でした。
RLとEAは、model augmentationというフィルタの数や深さを増やすテクニックを用いることで、1.5%まで下がりました。
Liu et al. (2018b)によると、RSvsRL/EAの差は更に小さく、CIFAR-10のtest errorで3.9%vs3.75%、ImageNetのvalidation errorで21%vs20.3%でした。
**ベイズ最適化(BO)**は最もポピュラーなハイパラ最適化手法の1つですが、あまりNASには使われていませんでした。
なぜなら、典型的なBOのツールボックスはGaussian processe(GP)に基づいており、低次元の連続変数の最適化にフォーカスしていたからです。
Swersky et al. (2013)とKandasamy et al.(2018)は、古典的なGPベースのBOを構造探索に使うためのカーネル関数を導きました。
対照的に、Tree Parzen estimators (Bergstra et al., 2011)やランダムフォレスト(Hutter et al., 2011)
などツリーベースのモデルを用いた研究もあります。(Tree Parzenはこちらの資料がわかりやすいです)
高次元の条件付き空間を探索することで、様々なタスクでSOTAを達成しました。
また構造とハイパーパラメータを同時に最適化することも可能です。(Bergstra et al., 2013; Domhan et al., 2015; Mendoza et al., 2016; Zela et al., 2018)
完全な比較はまだありませんが、BOはEAよりも優れた性能を発揮できるようだというpreliminary evidenceも報告されています(Klein et al., 2018)。
Negrinho and Gordon (2017)とWistuba (2017)は探索空間に木構造を導入し、モンテカルロ木探索を用いました。
Elsken et al. (2017)はシンプルで高性能な山登り法のアルゴリズムを提案しました。これは良い性能の方向に貪欲法を用いて探索するもので、洗練された探索メカニズムを必要としない所がポイントです。
上記の手法は離散空間を採用していますが、Liu et al. (2019)は連続緩和(continuous relaxation)を用いて勾配ベースの最適化を適用できるようにしました。
いわゆるDARTSです。こちらの資料がわかりやすいです。
特定のレイヤで行われる操作$o_{i}$を(畳み込みやプーリングに)変更するのではなく、操作の集合{$o_{1}, ... , o_{m}$}の凸結合(convex combination)を計算しました。
具体的には、レイヤへの入力xが与えられた時、出力yは凸結合αを用いて
$y = \sum_{i=1}^{m}α_io_i$
と表せます。この時、αは
$α_i\geq 0$
$\sum_{i=1}^{m}α_i=1$
を満たし、効果的にNNの構造をパラメトライズできていると言えます。
Liu et al.(2019)は重みと構造の両方を交互に勾配降下法で最適化しました。この時、重みの学習にはtrainデータを、構造の学習にはvalidデータを用いています。(構造のパラメータにはとして凸結合αを用いています。)
最終的に、$α_i$が最大になる操作iが各レイヤで採用され、離散的な構造を得ることができます。
Xie et al. (2019)とCai et al.(2019)は、αの加重を最適化する代わりに操作iの分布をパラメトライズして最適化しました。
Shin et al. (2018)とAhmed and Torresani(2018) は勾配ベースの手法を採用しましたが、それぞれレイヤのハイパラと接続パターンの最適化にフォーカスしました。
パフォーマンス推定(performance estimation strategy)
前セクションで説明した探索戦略は、未知のデータに対するパフォーマンスを最大化する構造を選ぶことを目的としています。
当然、探索戦略が選んだNNの構造A∈Aのパフォーマンスをどうにかして評価する必要があります。
最も簡単な方法は、(一般的な機械学習手法で用いられているように)trainデータとvalidデータを分割し、前者で学習&後者で評価することでしょう。
しかし、構造Aを頻繁にフルスクラッチで生成して評価するのは非常に計算コストがかかります。
そこで、様々な高速化手法が開発されました。
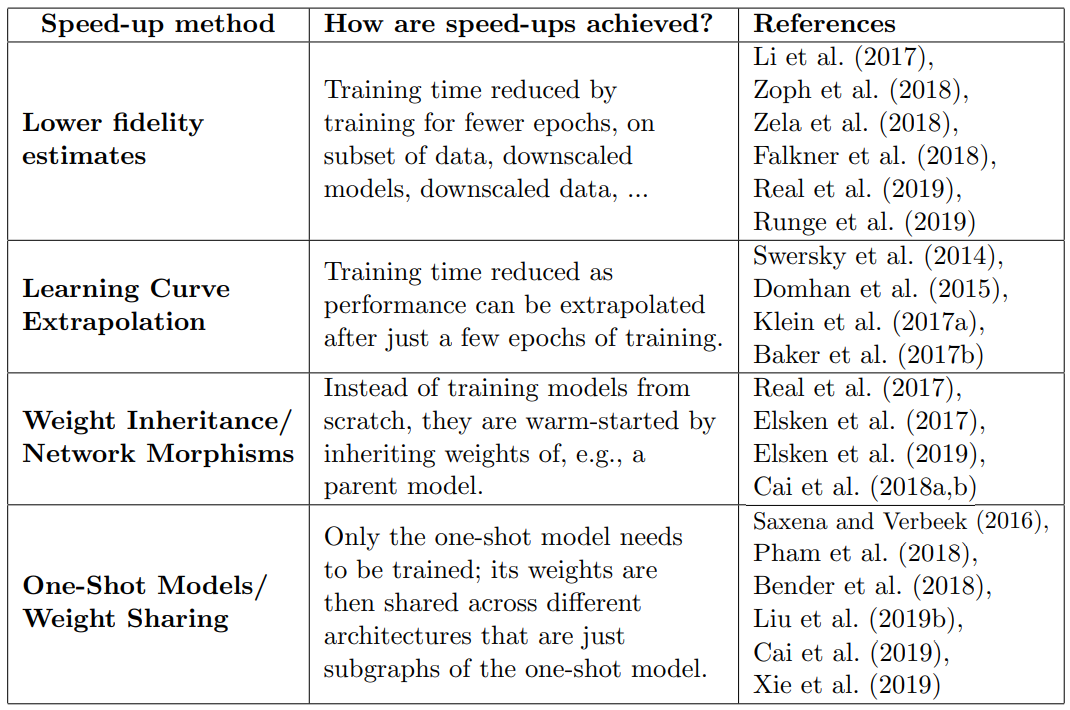
Table1 : NAS高速化手法の概観
NASの高速化手法は大きく分けて4種類です。
1つ目の方法は、実際のパフォーマンスに対し忠実度(fidelity)の低い指標で推定することです。(これをproxy metrics、代理指標といいます)
fidelityの低い例として、以下のようなものがあります。
・短い学習時間で学習する(Zoph et al., 2018; Zela et al., 2018)
・データのサブセットしか使わない(Klein et al., 2017)
・低解像度の画像を使う(Chrabaszcz et al., 2017)
・レイヤ毎のフィルタやCellを減らす(Zoph et al., 2018; Real et al., 2019)
低fidelityで近似することで計算コストを抑えることができます。
一般的には性能が低くなる方向にバイアスがかかりますが、探索戦略が各構造の順位に依るならば問題ではありません。
しかし最近の研究では、あまりにfidelityが低く、かつ実際の評価との差が大きい場合、相対順位も変わってしまうことが示されています(Zela et al., 2018)。
2つ目の方法は、learning curve extrapolation(学習曲線外挿)です。(Swersky et al., 2014; Domhan et al., 2015; Klein et al., 2017a; Baker et al., 2017b; Rawal and Miikkulainen, 2018)
Domhan et al. (2015)は初期学習曲線を外挿し、パフォーマンスが低いと予測されたものを打ち切ることで全体の探索時間を短縮します。
Swersky et al. (2014), Klein et al. (2017a), Baker et al. (2017b)、Rawal and Miikkulainen (2018)は、どの部分学習曲線が将来有望そうかということに着目しました。
Liu et al. (2018)は、新しい構造のパフォーマンスを予測するために代理のモデルを学習することを提案しました。当該の論文では学習曲線外挿は採用していませんが、学習時よりも大きいサイズのCellを外挿することでパフォーマンスを予測するというテクニックを用いています。
パフォーマンス予測の高速化の一番の課題は、やはり広い探索空間を少ない評価回数で評価しないといけないという点です。
そこで、3つ目の手法であるWeight Inheritance/Network Morphismを紹介します。
これは、訓練済みのNNの重みを新しいNNの重みの初期値に使うというもので、考え方としてはFine tuningに非常に似ていると思います。
Network morphisms (Wei et al., 2016)はNNの構造が変異する(一部の構造を保ったままChild networkを生成する)というものです。詳細はFigure4を参照して下さい。
イテレーションの度にNNをフルスクラッチで学習するコストが削減されるので、計算コストが大幅に下がるのがわかると思います。(Elsken et al., 2017; Cai et al., 2018a,b; Jin et al., 2018)では数GPU台x日まで低下させることができました。
Network morphismsの特徴に**探索空間の上界が構造のサイズによってバウンドされない(Elsken et al., 2017)**というものがあります。
複雑で柔軟な構造が見つかる可能性もある一方、過度に複雑で巨大な構造が生成されてしまう可能性もあります。
そこでElsken et al. (2019)は、近似Network morphismを用いることで構造を縮小化させています。
4つ目の手法はOne-Shot NASです。
生成されうる全ての構造は1つのスーパーグラフのサブグラフであると仮定します。(つまり、サブグラフ間で重みを共有します)
スーパーグラフを1回(One-Shot)で学習しようというのがこの手法です。
考え方としてはWeight sharingに非常に似ていると思います。
(Saxena and Verbeek, 2016; Brock et al., 2017; Pham et al., 2018; Liu et al., 2019b; Bender et al., 2018; Cai et al., 2019; Xie et al., 2019)
One-Shot NASは、
①:スーパーグラフを1回学習する
②:スーパーグラフからサブグラフを抽出する
③:サブグラフの評価を行う
④:②と③を繰り返す
という流れになります。
学習が1回で済むので、とても高速です。
CIFAR-10のError rateにフォーカスすると、ENAS(Pham et al., 2018)は1GPU0.45dayで2.89%、ASNG-NAS(Akimoto et al., 2019)は1GPU0.11dayで2.83(±0.14)%を達成しました。
Zoph and Le, 2017が800GPUで21〜28日で3.6%だったことを考えると、どれほど高速になったかよくわかると思います。
しかし、One-Shotモデルはパフォーマンスを過小評価するバイアスが掛かりやすいという欠点(?)があります。
構造のよさに順位を付けることは可能なので、推定パフォーマンスと実際のパフォーマンスの相関が強いと仮定すれば何の問題もありません。
しかし2019年現在、実問題において推定パフォーマンスと実際のパフォーマンス強い相関が存在するかはまだ明らかではありません。(Bender et al., 2018), (Sciuto et al., 2019)
One-Shot NASを実現する各手法は、1度のスーパーグラフの学習をどうやって行うかという所に違いがあります。
ENAS(Pham et al., 2018)はRNN controllerを用いて構造をサンプルし、強化学習によって得られた勾配を用いて学習を行います。
DARTS (Liu et al., 2019)は先程紹介しましたが、連続緩和(continuous relaxation)を用いて凸結合を計算し、各エッジにおける操作の候補を混合して表現することで構造を学習します。
SNAS (Xie et al., 2019)はDARTSのように実数値の重みを最適化するのではなく、操作の候補の分布を最適化します。
Concrete distribution (Maddison et al., 2017), (Jang et al., 2017)とreparametrization (Kingma and Welling, 2014)を採用し離散分布を微分可能に緩和し、勾配ベースで学習しています。
こちらの資料がわかりやすいです。
ProxylessNAS (Cai et al., 2019)はOne-Shotで学習したスーパーグラフの値を保持する為に大量のGPUメモリを消費するという欠点を改善したもので、構造の重みを二値化して、各操作毎に1エッジを除いてマスクするというテクニックを使っています。
エッジがマスクされているかの確率はバイナリ化されたいくつかの構造をサンプリングしてBinaryConnect (Courbariaux et al., 2015)を用いることで学習され、対応する確率を更新します。
Bender et al. (2018)は(Dropoutのように)確率的にスーパーグラフの一部をマスクするというテクニックを採用しました。
上記の手法は学習中に分布を最適化しているのに対し、本手法は分布を固定していると考えることができます。
分布を固定して高性能の構造が得られるということは、Weight sharingと(慎重に選んだ)固定分布さえあればOne-Shot NASは実現可能であるということで、これはとても驚くべきことだと著者は述べています。
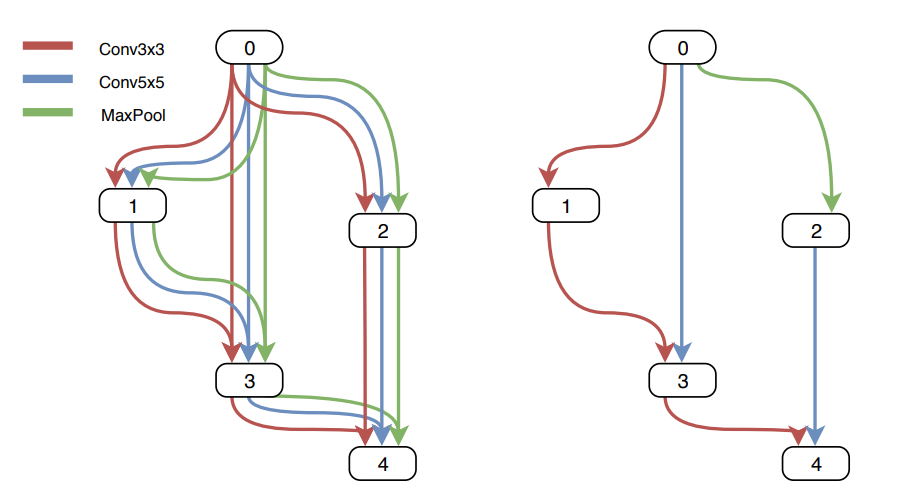
Figure5 : One-Shot NASのイラスト
図中左はスーパーグラフで、各ノードの操作の候補として「3x3畳み込み」「5x5畳み込み」「Maxプーリング」の3種類を採用しています。
図中右はスーパーグラフからサンプルされたサブグラフの1つです。
One-Shot NASに関連して、メタラーニングを紹介します。
これはHypernertworkという、Child networkを生成する構造を1度だけ学習する手法です。(Brock et al., 2017), (Zhang et al., 2019)
One-Shot NASのスーパーグラフと似ていますが、
・One-Shot NAS:スーパーグラフの一部がサブグラフ(スーパーグラフとサブグラフで重みを共有する)
・メタラーニングHypernertworkの一部がサンプルされ、それからChild networkを生成する(HypernertworkとChild networkで重みを共有するわけではない)
という違いがあります。
話をOne-Shot NASに戻します。
One-Shot NASでは、
・(当たり前ですが)スーパーグラフが探索空間を制限してしまう
・(ProxylessNASの項で述べたように)GPUのメモリを大量に消費するので、メモリが少ないと小さいスーパーグラフしか探索できない
・つまり、メモリが少ないと探索空間が制限されてしまう
という問題があるため、通常はCellベースの探索空間と組み合わせて使われます。
また2019年現在、One-Shotモデルはどのようなバイアスが発生するか十分にわかっていません。
例えば、どこの空間から探索するかという初期値のバイアスはOne-Shotモデルに大きく影響を与えてしまいます。
これによってNASの収束時間や、推定パフォーマンスと真のパフォーマンスとの相関の強弱も変わってきます。(Sciuto et al., 2019)
バイアスに対して、異なるパフォーマンス推定方法を用いたシステマティックな分析が行われることが望ましいと考えています。
今後の展望(Future Directions)
本セクションでは、NASに関する研究の現在と将来の方向性について説明します。
既存の研究の多くは画像分類にフォーカスしています。
他の(ハンドアセンブルの優れたNNが存在する)ドメインにおいては、そのようなNNよりも良い性能を出すことはまだ簡単ではないでしょう。
ドメイン知識を用いてベストな探索空間を定義することは簡単ですが、その場合はNASが生成したNNが既存のNNを超える(あるいは根本的に異なるNNを見つける)とは考えにくいです。
したがって、NASは画像分類以外の、まだあまり(人手でも)探索されていないドメインに適用すべきと考えています。
例として、画像復元(Suganuma et al., 2018)やセマンティックセグメンテーションsegmentation (Chen et al., 2018), (Nekrasov et al., 2018), (Liu et al., 2019a)、転移学習(Wong et al., 2018)、機械翻訳 (So et al., 2019)、強化学習(Runge et al., 2019)、RNNを用いた言語処理や音楽のモデリング(Greff et al., 2015), (Jozefowicz et al., 2015), (Zoph and Le, 2017), (Rawal and Miikkulainen, 2018)などが挙げられます。
さらに、今後はGANやSensor fusionへの応用も期待されます。
強化学習(Runge et al., 2019)について:深層強化学習にNASを応用する研究が行われており、CNNブロックとリカレントブロックを使った巨大でversatileな空間を勾配ネットワークとして利用しています。
また、マルチタスク問題(Liang et al., 2018; Meyerson and Miikkulainen, 2018)や多目的問題(Elsken et al., 2019; Dong et al., 2018; Zhou et al., 2018)のためのNAS手法の開発も期待されています。
推定パフォーマンスに加えて、未知のデータに対するリソースの測定効率も目的関数として使われます。
多目的NASはネットワーク圧縮(Han et al., 2016; Cheng et al., 2018)と密接であることを強調しておきます。
どちらも高パフォーマンスの効率的な構造を発見することを目的としているため、既存のネットワーク圧縮研究の一部(Han et al., 2015; Liu et al., 2017; Gordon et al., 2018; Liu et al., 2019c; Cao et al., 2019)はNASとみなすことができます。
逆に、既存のNAS研究の一部(Saxena and Verbeek, 2016; Liu et al., 2019b; Xie et al., 2019)はネットワーク圧縮をみなすことができます。
同様に、強化学習の一部は多腕バンディット問題とみなすことができます。
Ramachandran and Le (2018)はOne-Shot NASを汎用的に応用しようとしています。
Cubuk et al. (2017)はNASによって生成されたNNはAdversarial Robustnessを持つと述べています。
Adversarial Robustness:Adversarial Examplesに対するロバスト性のこと。
Adversarial Examples:人間にはわからない摂動を与えることで、モデルが誤検知してしまう入力のこと。こちらのパンダとテナガザルの例が有名です。
より柔軟で一般的な探索空間を定義する研究もあります。
例えば、Cellベースの探索空間は画像分類の異なるタスク間で転移性が高い(つまり、CIFAR-10で性能がいいモデルを元に、簡単にImageNetで性能がいいモデルを作ることができる)ですが、人の経験に基づいている部分が大きいため他のドメインに転用することができません。
より一般的な階層構造を表現できる探索空間が見つかれば、NASはより汎用的になるでしょう。
詳細は、この方向性の最初の研究であるLiu et al. (2018, 2019)を参照して下さい。
更に、一般的な探索空間は畳み込みやプーリング等の要素に基づいていますが、未知のレイヤタイプを表現することはできません。
この制限を超えることで、NASの力は大幅に向上するはずです。
また、NASの適切な比較や再現性の確保に関する研究も進んでいます。
NAS研究の多くはCIFAR-10で実験を行い、計算コスト(GPU台x日)と精度(test error)をレポートしていますが、探索空間やData augmentation、正則化、GPUの種類など様々な要因によって結果は変わります。
例えば、CIFAR-10では以下のような方法でパフォーマンスが向上する事が知られています。
・cosine annealing learning rate schedule (Loshchilov and Hutter, 2017)
・data augmentation by CutOut(Devries and Taylor, 2017)
・MixUp (Zhang et al., 2017)
・a combination of factors(Cubuk et al., 2018)
・Shake-Shake regularization (Gastaldi, 2017)
・ScheduledDropPath (Zoph et al., 2018)
多くの論文は「NASの手法」+「性能向上の手法」を組み合わせて実験を行い論文を書いているので、NASの手法のみを適切に比較できていない、と著者は主張しています。
したがって、NAS-Bench-101(Ying et al., 2019)の様な、一般的なNAS専用のベンチマークを使用することが重要だと考えてます。
NAS-Bench-101についてはこちらでまとめています。
NAS-Bench-101では計算リソースを使わずにNAS手法を比較する事ができます。
はじめにNASはAutoMLのサブフィールドですと書きましたが、NASを独立に研究するのではなくオープンソースのAutoMLシステムの一部として研究することも興味深いです。そこではハイパラ最適化(Mendoza et al., 2016; Real et al., 2017; Zela et al., 2018)やData augmentation pipeline最適化(Cubuk et al., 2018)の研究が進んでいます。
終わりに
NASはいくつかのタスクで優れたパフォーマンスを発揮していますが、2019年現在「なぜ特定の構造が良い性能を発揮するのか」「独立して導かれた構造がどのくらい似ているか」という疑問に関する見通しはあまり立っていません。
共通のモチーフ(繰り返し構造)を特定して理解することが、様々な問題における高性能化と一般化へのカギとなるでしょう。
ここまでお読み頂きありがとうございました。
他のNASの手法についても、こちらが大変良くまとまっています。
質問などありましたらコメントいただくか、本人のTwitterまでご連絡下さい。
これからもNASの記事を作成する予定なので、いいねと思ったらぜひフォロー, thumbs-up&拡散をお願いします!