index
第1回（準備と簡単な例）
第2回（動くマテリアル）
第3回（形を作る）
(イマココ)第4回（形を動かす）
第5回（テクスチャサンプリング*N）
概要
第2回、第3回の内容を応用して動く図形を作ります。
応用編ということで、記事としてのためになる度は低いかもしれません（元から低い気もしますが！）。
動画を見て、自分で同じことができそうだと思った方は記事を読む前にやってみるのも一興だと思います。
https://vine.co/v/OXqWQXwxzAL
円を動かす
円の描画には前回作成したMaterialFunctionを使用します。
Timeに応じて中心の座標を変化させれば動く円の出来上がりです。
物体を動かす場合にゲームプログラミングでよく使用される方法というと
- 現在の座標を記憶しておく
- それに速度*Δtを加算して次のフレームの座標を求める
- 1,2を繰り返す
という感じだと思いますが、
マテリアル自体で「座標を記憶しておく」ことが容易ではありません（多分）。
今回とる方法は
- 現在の時間から座標を求める方程式を作る
という、より原始的（？）な考え方によるものです。
ゲームにおいてはプレイヤーによる入力や他のオブジェクトによる干渉があり通用しない場合が多いため、あまり馴染みがないかもしれません。
等速直線運動
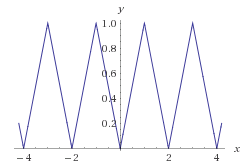
まっすぐ一定の速度での運動は以下のように表されます。
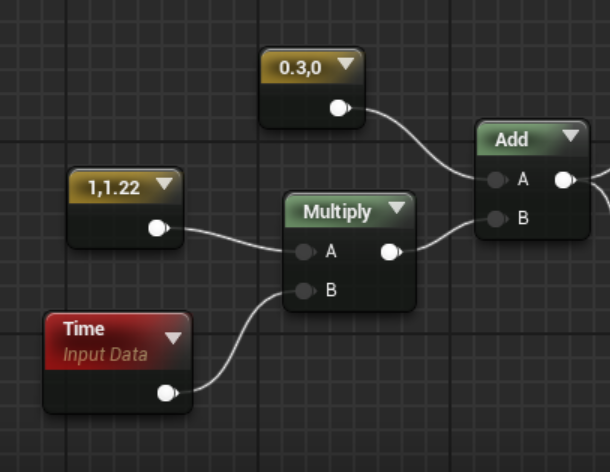
座標＝初期位置＋速度*時間
たとえば初期位置(0.3,0),速度(1,1.22)とした場合、以下のようなグラフになります。
端で反射させる
等速直線運動として導いた座標を鏡写しにしてX,Y成分それぞれを(0,1)の範囲に収めます。
この手の「マッピング」的な計算を考える場合、グラフで考えるのが楽です。
欲しいのは下図のようなグラフです。
(0,1)の範囲ではそのまま、それをはみ出すと戻ってくるという振る舞いを表現しています。
ここで、方程式からグラフを生成してくれるWeb上のツールをふたつ紹介しておきます。
wolfram alpha
http://www.wolframalpha.com/
グラフ描画以外にも色んな質問に答えてくれたりする謎のテクノロジーです。
Desmosグラフ計算機
https://www.desmos.com/calculator
グラフ特化。複数のグラフを表示したりパラメータを変化させてアニメーション的なこともできます。
先のグラフはwolfram alphaで表示させたもので、
こんな方程式になっています（もっとスマートな式があるかもしれませんが）。
1-abs(1-(frac(abs(x/2))*2))
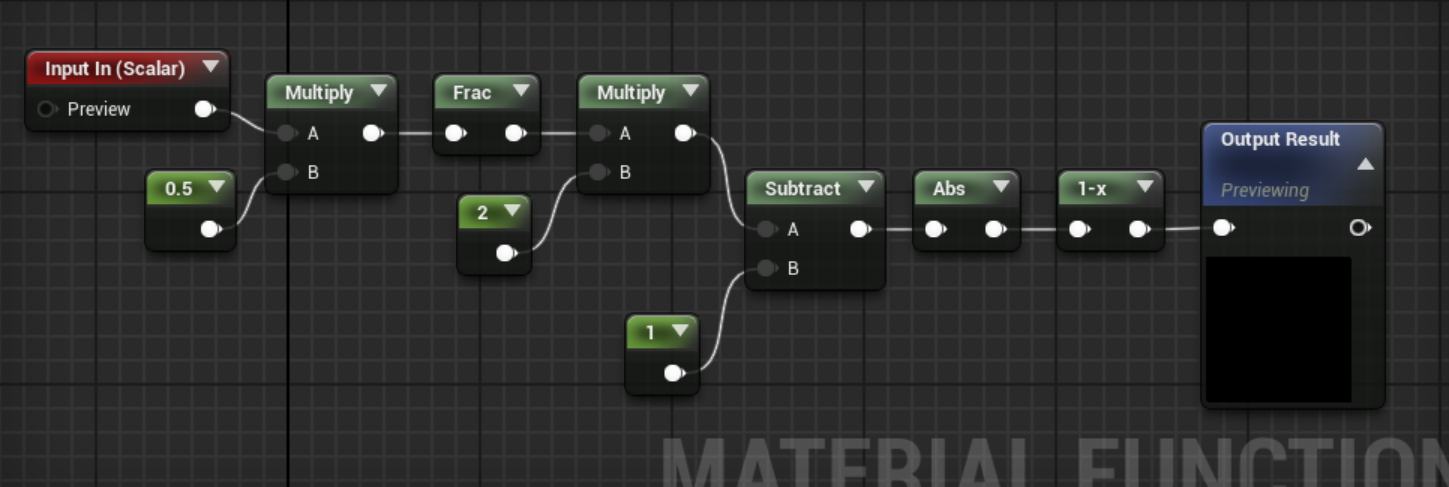
こいつをMaterialEditorで再現すれば反射運動の完成というわけです。
またまたMaterialFunctionにしておきます。
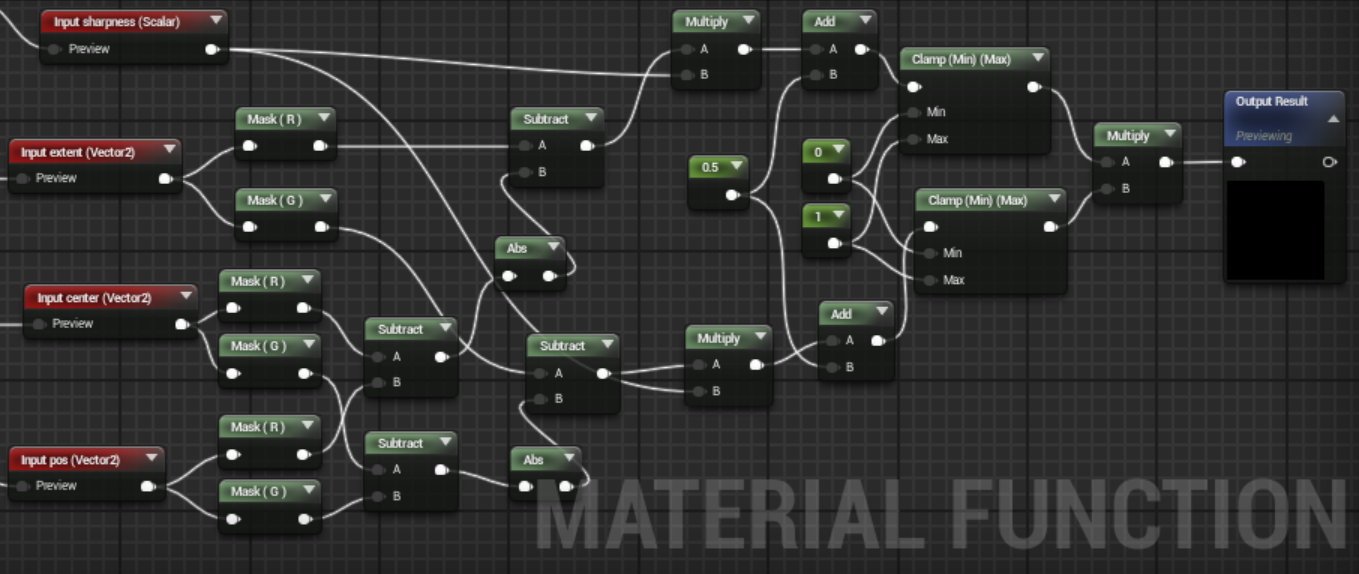
四角を表示する
一見煩雑ですが、ロジックは円のときとほぼ同様です。
ポイントは縦と横それぞれで計算した値を乗算するところです。
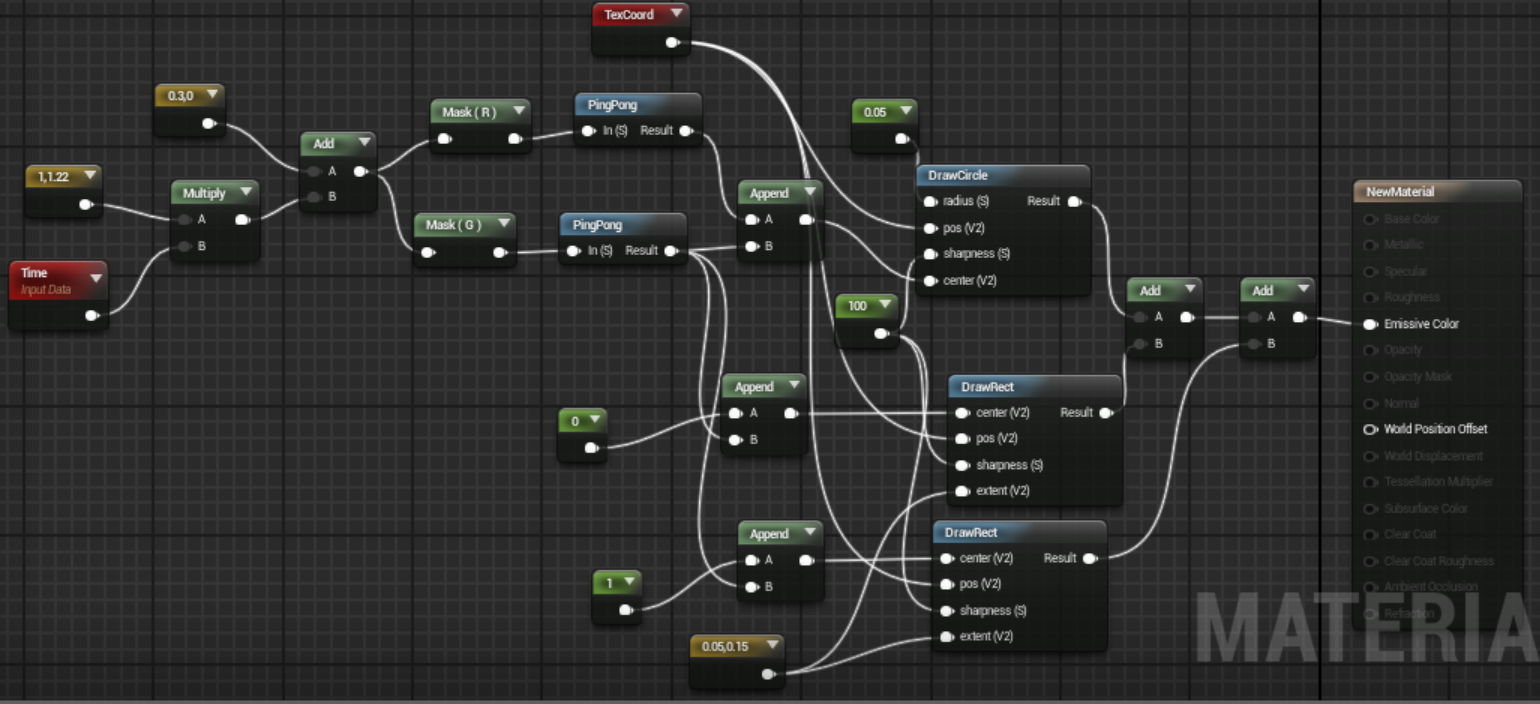
組み合わせる
それらを組み合わせて、こうじゃ・・・！
- 円の座標を前半で計算し、そのY成分を左右の長方形に渡しています。
- 複数の図形を描画する場合は適切なブレンドを考える必要があります。黒地に白の描画であればAddで充分です。
以上です。
次はちょっと普通のやつになる予定です。