こんにちは。ナビタイムジャパンのデルタです。
今年4月に新卒で入社して、現在は研究開発部門でアルゴリズム開発エンジニアをしています。
これは NAVITIME JAPAN Advent Calendar 2019 16日目の記事です。
この記事では機械学習初心者向けに、クラスタリングの手法として広く使われているk-meansを実際に実装してみようと思います。
最初に
クラスタリングとは
そもそもクラスタリングとは?という方もいらっしゃると思うので少しだけ解説をします。
一言に機械学習といっても色々なものがあります。
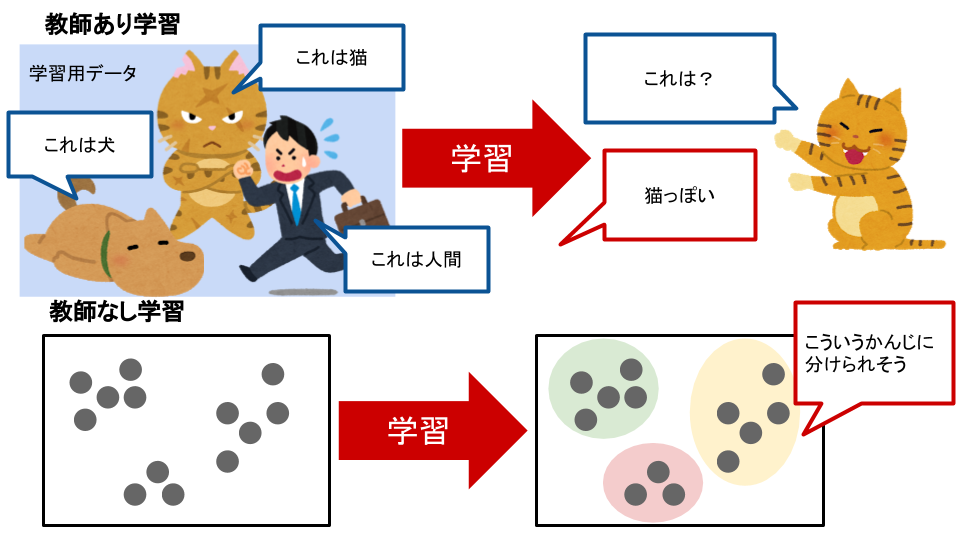
その分類方法もまた様々なのですが、初学者向けの書籍等で言及されることが多いのは「教師あり学習」「教師なし学習」の二種類です。1
「教師あり学習」はあらかじめ「正解」のデータ(学習用データ)を用意し、それと同じ傾向の答えを導き出す学習方法です。
対して「教師なし学習」は「正解」のデータがないものに対して、構造の解析を行い答えを導き出す学習方法です。
クラスタリングは「教師なし学習」に分類されます。
いくつかの特徴量を持ったデータの集合を学習用データなしに自動的に分類するのがクラスタリングです。
自分で実装する意義
機械学習のためのツールやライブラリは今とても充実しているので、機械学習を開発に取り入れる際にも色々な選択肢が考えられます。
例えば、機械学習PaaSであるAzure Machine LearningやAmazon SageMakerを利用するとがっつりプログラミングすることなく機械学習を始めることができます。
機械学習の結果だけがサクッと欲しいときはGoogleやMicrosoftが提供しているAPIを使う手もあります。
また、scikit-learn(サイキット・ラーン)などのライブラリを利用すると簡単に精度の良い機械学習のアルゴリズムを使用することができます。
優秀なライブラリの存在もあり、使うだけであれば特別な理由がない限りアルゴリズムを自分で実装する必要はないです。
しかし、自分で実装することによって次のようなうれしい恩恵が得られます。
- アルゴリズムの中身を深く知ることになる・理解が深まる
- アルゴリズムの強みや弱点が見えてくる
- 自分のやりたいことに対してどのアルゴリズムを使えばいいのかがわかるようになる
- アルゴリズムと仲良くなって自信がつく
優秀なツールを使うことで楽に品質の良いものを作ることができるのは素晴らしいことです。
その上で自分の使っているツールの中身がどのようなものか理解すればさらなるプロダクトの品質向上に繋がります。
また、アルゴリズムと仲良くなって愛着が湧くとただツールを使うだけよりも開発が楽しくなるので、個人的には4番目も重要だなあと思います!
それはそうと
12月も半ばとなりましたが、みなさんは年末どうすごされる予定でしょうか。
わたしは毎年年末はこれを見て過ごします。

紅白のコレですね。
おや…?
不思議な力によって、なぜか完全に真っ黒になってしまいました…。
これでは幸せな年末を迎えられそうにないですね。
ところで
紅白(だった)コレですが、どうやら左と右の円の二つで構成されているようです。
ここで「教師なし学習」を思い出してほしいのですが、
「教師なし学習」とは
「正解」のデータがないものに対して、構造の解析を行い答えを導き出す学習方法
です。
また、クラスタリングとは教師なし学習の一つで「データの集合を分類」することでした。
明らかに2つに分類されそうな構造を持つこの点群はクラスタリングできそうですよね!
黒一色になってしまったものを紅白に戻して幸せな年末を迎えるためにクラスタリングを実装していきましょう。
環境構築(Google Colaboratory)
データ分析にはJupyter Notebookというツールがよく使用されています。
セルと呼ばれる部分にコードの入力ができ、ノートのようにメモや解説を書き込むことも可能です。
セルごとに実行し、その実行結果の保存もできます。
言語は主にPythonが使用できます。
このJupyter Notebookを完全にクラウドで実行できるのがGoogle Colaboratoryです。
既にローカルにあるPythonの環境を壊さず、また何もインストールせずに開くだけで使えるので大変便利です。
また、本記事の実装にも使用している
- numpy (多次元配列計算を高速化するライブラリ)
- matplotlib (グラフ描画のためのライブラリ)
などの各種ライブラリもインストールすることなく使用できます。
今回はこのGoogle Colaboratoryを用いて実装をしていきます。
サンプルデータ作成
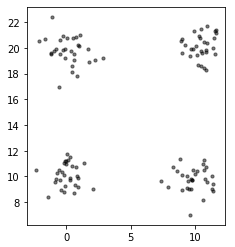
まずは例の黒い点群を再現していきましょう。
# サンプルデータ作成
import numpy as np
# seed値固定
np.random.seed(874)
# x座標
x = np.r_[np.random.normal(size=1000,loc=0,scale=1),
np.random.normal(size=1000,loc=4,scale=1)]
# y座標
y = np.r_[np.random.normal(size=1000,loc=10,scale=1),
np.random.normal(size=1000,loc=10,scale=1)]
data = np.c_[x, y]
# 可視化処理
import matplotlib.pyplot as plt
% matplotlib inline
p = plt.subplot()
p.scatter(data[:,0], data[:,1], c = "black", alpha = 0.5)
p.set_aspect('equal')
plt.show()
np.random.normalで正規分布に従う乱数を出力することができます。
k-meansクラスタリングの実装
クラスタリング手法には、広く使われていて手軽に実装できるk-meansを使ってみましょう。
アルゴリズム解説
k-meansは以下のようにクラスタリングを進めます。
- クラスタ数(何種類に分類したいか)を決める
- クラスタ数だけ中心点を用意する
- 各データ点は一番近い中心点を自分の所属するクラスタとする
- 同一クラスタに所属するデータ点の重心を新しい中心点とする
- 収束する(中心点が移動しなくなる)まで2から4を繰り返す
実際に動かしてみるとこんな感じになります。
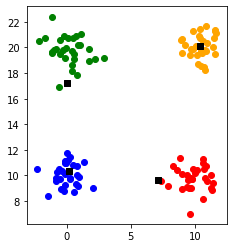
分類する元データはこれです。
1. クラスタ数(何種類に分類したいか)を決める
今回は4つとします。
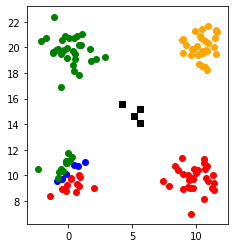
各クラスタを赤・青・緑・黄色で分けます。
最初は各点にランダムにクラスタを割り振りました。
2. クラスタ数だけ中心点を用意する
4つの黒い四角の点が中心点です。
3. 各データ点は一番近い中心点を自分の所属するクラスタとする
各点は一番距離が近い中心点に所属しました。
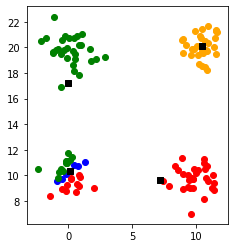
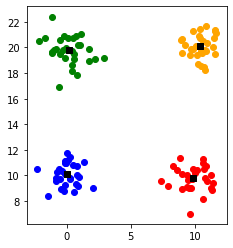
4. 同一クラスタに所属するデータ点の重心を新しい中心点とする
中心点は各クラスタの重心に更新されました。
再び3の処理を行い各点のクラスタの所属を更新します。
中心点を更新します。
ここまでくると中心点はこれ以上動かなくなるので収束と判定されます。
実装
いよいよk-meansを実装して紅白にクラスタリングしていきます。
実装はとてもシンプルです。
# クラスタ数
n_clusters = 2
# 最大ループ数
max_iter = 300
# 所属クラスタ
clusters = np.random.randint(0, n_clusters, data.shape[0])
まずは初期化からしていきます。
最大ループ数は収束しなかった場合のループ回数の上限です。
所属クラスタは最初はランダムに決めました。
np.random.randintで任意の範囲の整数の乱数を出力することができます。
ループ処理に入っていきます。
for _ in range(max_iter):
# 中心点の更新
# 各クラスタのデータ点の平均をとる
centroids = np.array([data[clusters == n, :].mean(axis = 0) for n in range(n_clusters)])
# 所属クラスタの更新
# 一番近い中心点のクラスタを所属クラスタに更新する
# np.linalg.normでノルムが計算できる
# argminで最小値のインデックスを取得できる
new_clusters = np.array([np.linalg.norm(data - c, axis = 1) for c in centroids]).argmin(axis = 0)
# 空のクラスタがあった場合は中心点をランダムな点に割り当てなおす
for n in range(n_clusters):
if not np.any(new_clusters == n):
centroids[n] = data[np.random.choice(data.shape[0], 1), :]
# 収束判定
if np.allclose(clusters, new_clusters):
break
clusters = new_clusters
途中で空のクラスタができると失敗してしまうので、今回は中心点を割り当て直す処理を加えました。
最後に可視化をしてあげましょう。
p = plt.subplot()
p.scatter(data[clusters==0, 0], data[clusters==0, 1], c = 'red')
p.scatter(data[clusters==1, 0], data[clusters==1, 1], c = 'white', edgecolors='black')
# 中心点
p.scatter(centroids[:, 0], centroids[:, 1], color='orange', marker='s')
p.set_aspect('equal')
plt.show()
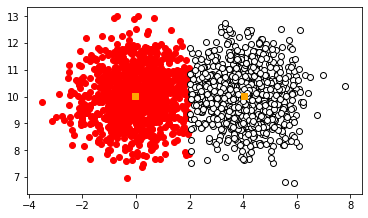
実際に動かしてみると………。
無事に紅白に戻すことができました!!
scikit-learnを使う
ここまで頑張って実装してきましたが、上述したscikit-learnというライブラリを使うともっと簡単にk-meansが実装できます。
from sklearn.cluster import KMeans
# k-means
km = KMeans(n_clusters=2, init='k-means++', n_init=10, max_iter=300, tol=1e-04, random_state=0)
clusters_sklearn = km.fit_predict(data)
# 可視化処理
p = plt.subplot()
p.scatter(data[clusters_sklearn==0, 0], data[clusters_sklearn==0, 1], c = 'red')
p.scatter(data[clusters_sklearn==1, 0], data[clusters_sklearn==1, 1], c = 'white', edgecolors='black')
p.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[: ,1], color='orange', marker='s')
p.set_aspect('equal')
plt.show()
2行でクラスタリングができてしまいました!
とても便利ですね。
自分で実装するより精度も高いので、実際に使う時は特別な理由がない限りscikit-learnを利用すればいいと思います。
補足
ちなみにk-meansには欠点があります。2
今回のようにランダムで初期クラスタを決定すると、中心点の初期位置が近くなり、意図しないクラスタリングになることがあります。
この欠点を補う方法として、k-means++という方法があります。
k-means++は中心点の初期位置がお互いに離れるようにしてあげる方法です。
k-means++を用いることで適切なクラスタリングができるようになるだけではなく、計算速度も向上する(ループ回数が減る)ので、興味のある方はぜひ調べてみてください。
まとめ
k-meansについて簡単に解説と実装をしてみました。
今回実装したものはGistで公開しています。
https://gist.github.com/ajitsuki/041c57e75418f046d7e6ea05372e84be
少しでもk-meansと仲良くなれたなら幸いです。
最後になりますが、弊社でも機械学習を用いて
といったサービスや機能を開発しています!
興味のある方はぜひ触ってみてくださいね。
それではみなさん、よい年末を!
参考文献
Alice Zheng, Amanda Casari 機械学習のための特徴量エンジニアリング
k-meansよりもちょっとイケてるk-means++
k-meansとk-means++を視覚的に理解する~Pythonにてスクラッチから~