何をやるか?
超シンプルなドラクエ風ターン制バトルを作ってQ学習させてみます。
数%の確率でしか世界を救えない勇者くんを、Q学習で賢くすることが目的です。
なお、ゲーム部分・Q学習の実装については解説しますが、Q学習そのものは解説しません。
Q学習の詳しい理論を知りたい方は、こちらの良記事を一つずつ読んでいくと幸せになれます。
今さら聞けない強化学習(1):状態価値関数とBellman方程式
読んでもらいたい人
- OpenAI Gymなどの既存のシミュレーション環境ではなく、自分でゲームを作って色々弄ってみたい方。
- Q学習の理論はなんとなく知ってるんだけど、「どうやって実装すれば良いかわからない!」という方。
ゲームをつくる
ルールはシンプルに、以下のように設計します。
- 勇者 vs 魔王の1対1
- 魔王のとる行動は「攻撃」のみ
- 勇者のとれる行動は「攻撃」と「回復」の2択
- 行動順序は、各キャラの素早さに一定の乱数を掛けてソートさせることで決定する
キャラクタークラスの実装
それでは早速、ゲーム本体の実装をしていきましょう。
まずはキャラクタークラスです。
class Character(object):
""" キャラクタークラス"""
ACTIONS = {0: "攻撃", 1: "回復"}
def __init__(self, hp, max_hp, attack, defence, agillity, intelligence, name):
self.hp = hp # 現在のHP
self.max_hp = max_hp # 最大HP
self.attack = attack # 攻撃力
self.defence = defence # 防御力
self.agillity = agillity # 素早さ
self.intelligence = intelligence # 賢さ
self.name = name # キャラクター名
# ステータス文字列を返す
def get_status_s(self):
return "[{}] HP:{}/{} ATK:{} DEF:{} AGI:{} INT:{}".format(
self.name, self.hp, self.max_hp, self.attack, self.defence, self.agillity, self.intelligence)
def action(self, target, action):
# 攻撃
if action == 0:
# 攻撃力 - 防御力のダメージ計算
damage = self.attack - target.defence
draw_damage = damage # ログ用
# 相手の残りHPがダメージ量を下回っていたら、残りHPちょうどのダメージとする
if target.hp < damage:
damage = target.hp
# ダメージを与える
target.hp -= damage
# 戦闘ログを返す
return "{}は{}に{}のダメージを与えた".format(
self.name, target.name, draw_damage)
# 回復
elif action == 1:
# 回復量をINTの値とする
heal_points = self.intelligence
draw_heal_points = heal_points # ログ用
# 最大HPまで回復できるなら、最大HP - 現在のHPを回復量とする
if self.hp + heal_points > self.max_hp:
heal_points = self.max_hp - self.hp
# 回復
self.hp += heal_points
# 戦闘ログを返す
return "{}はHPを{}回復した".format(
self.name, draw_heal_points)
今回のバトル設計はシンプルなので、プレイヤーと敵を区別することなく1つのクラスにまとめてしまっています。
各キャラクター(勇者と魔王)は、
- HP(体力)
- ATTACK(攻撃力)
- DEFENCE(防御力)
- AGILLITY(素早さ)
- INTELIGENCE(賢さ)
のステータスを持ちます。
「攻撃」でのダメージ計算は、
「(自分の攻撃力)ー(相手の防御力)」
という単純な式で計算しています。
また、「回復」コマンドでの回復量は賢さの数値そのままとしました。
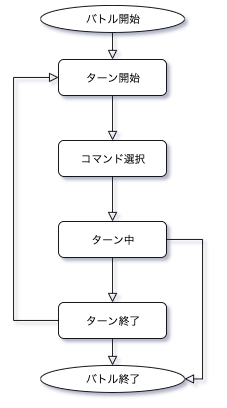
バトル設計の全体像(状態遷移)
続いてバトル本体を実装していきます。
初めに、バトルの全体像(状態遷移)について理解しておく必要があります。
class GameState(Enum):
""" ゲーム状態管理クラス"""
TURN_START = auto() # ターン開始
COMMAND_SELECT = auto() # コマンド選択
TURN_NOW = auto() # ターン中(各キャラ行動)
TURN_END = auto() # ターン終了
GAME_END = auto() # ゲーム終了
バトルには上記の通り、
「ターン開始」「コマンド選択」「ターン中」「ターン終了」「ゲーム終了」
の5つの状態があります。
状態遷移図で表すと下図のようになります。
このように、「ターン開始」状態から「ターン終了」状態までの遷移を、「ゲーム終了」状態になるまで(勇者か魔王のHPが0になるまで)延々とループさせるのがバトル設計の基本になります。
バトル本体の実装
それでは、バトル本体の実装です。
先にコード全体をみておきます。
class Game():
""" ゲーム本体"""
HERO_MAX_HP = 20
MAOU_MAX_HP = 50
def __init__(self):
# キャラクターを生成
self.hero = Character(
Game.HERO_MAX_HP, Game.HERO_MAX_HP, 4, 1, 5, 7, "勇者")
self.maou = Character(
Game.MAOU_MAX_HP, Game.MAOU_MAX_HP, 5, 2, 6, 3, "魔王")
# キャラクターリストに追加
self.characters = []
self.characters.append(self.hero)
self.characters.append(self.maou)
# 状態遷移用の変数を定義
self.game_state = GameState.TURN_START
# ターン数
self.turn = 1
# 戦闘ログを保存するための文字列
self.log = ""
# 1ターン毎にゲームを進める
def step(self, action):
# メインループ
while (True):
if self.game_state == GameState.TURN_START:
self.__turn_start()
elif self.game_state == GameState.COMMAND_SELECT:
self.__command_select(action) # 行動を渡す
elif self.game_state == GameState.TURN_NOW:
self.__turn_now()
elif self.game_state == GameState.TURN_END:
self.__turn_end()
break # ターン終了でもループを抜ける
elif self.game_state == GameState.GAME_END:
self.__game_end()
break
# ゲームが終了したかどうか
done = False
if self.game_state == GameState.GAME_END:
done = True
# 「状態s、報酬r、ゲームエンドかどうか」を返す
return (self.hero.hp, self.maou.hp), self.reward, done
# ゲームを1ターン目の状態に初期化
def reset(self):
self.__init__()
return (self.hero.hp, self.maou.hp)
# 戦闘ログを描画
def draw(self):
print(self.log, end="")
def __turn_start(self):
# 状態遷移
self.game_state = GameState.COMMAND_SELECT
# ログを初期化
self.log = ""
# 描画
s = " *** ターン" + str(self.turn) + " ***"
self.__save_log("\033[36m{}\033[0m".format(s))
self.__save_log(self.hero.get_status_s())
self.__save_log(self.maou.get_status_s())
def __command_select(self, action):
# 行動選択
self.action = action
# キャラクターを乱数0.5〜1.5の素早さ順にソートし、キューに格納
self.character_que = deque(sorted(self.characters,
key=lambda c: c.agillity*random.uniform(0.5, 1.5)))
# 状態遷移
self.game_state = GameState.TURN_NOW
# ログ保存
self.__save_log("コマンド選択 -> " + Character.ACTIONS[self.action])
def __turn_now(self):
# キャラクターキューから逐次行動
if len(self.character_que) > 0:
now_character = self.character_que.popleft()
if now_character is self.hero:
s = now_character.action(self.maou, self.action)
elif now_character is self.maou:
s = now_character.action(self.hero, action=0) # 魔王は常に攻撃
# ログを保存
self.__save_log(s)
# HPが0以下ならゲームエンド
for c in self.characters:
if c.hp <= 0:
self.game_state = GameState.GAME_END
return
# 全員行動終了したらターンエンド
if len(self.character_que) == 0:
self.game_state = GameState.TURN_END
return
def __turn_end(self):
# 報酬を設定
self.reward = 0
# キャラクターキューの初期化
self.character_que = deque()
# ターン経過
self.turn += 1
# 状態遷移
self.game_state = GameState.TURN_START
def __game_end(self):
if self.hero.hp <= 0:
self.__save_log("\033[31m{}\033[0m".format("勇者は死んでしまった"))
self.reward = -1 # 報酬を設定
elif self.maou.hp <= 0:
self.__save_log("\033[32m{}\033[0m".format("魔王をやっつけた"))
self.reward = 1 # 報酬を設定
self.__save_log("-----ゲームエンド-----")
def __save_log(self, s):
self.log += s + "\n"
少々コードが長いですが、Q学習で重要な部分は2つだけです。
1つ目は、step()メソッドです。ここがバトルのメイン部分になります。
# 1ターン毎にゲームを進める
def step(self, action):
# メインループ
while (True):
if self.game_state == GameState.TURN_START:
self.__turn_start()
elif self.game_state == GameState.COMMAND_SELECT:
self.__command_select(action) # 行動を渡す
elif self.game_state == GameState.TURN_NOW:
self.__turn_now()
elif self.game_state == GameState.TURN_END:
self.__turn_end()
break # ターン終了でもループを抜ける
elif self.game_state == GameState.GAME_END:
self.__game_end()
break
# ゲームが終了したかどうか
done = False
if self.game_state == GameState.GAME_END:
done = True
# 「状態s、報酬r、ゲームエンドかどうか」を返す
return (self.hero.hp, self.maou.hp), self.reward, done
基本的には、前述した状態遷移図と処理の流れは同じです。
ただし、Q学習では1ターン毎に現在の状態を評価しなくてはならないので、「ゲーム終了」状態に限らず、「ターン終了」状態でもメインループを抜けなければなりません。
「ターン終了」状態において、Q学習をするために評価しなくてはならない変数は、
- 「状態s」
- 「報酬r」
- 「ゲームエンドかどうかを判定するフラグ」
の3つです。
ゲームエンドかどうかについては、単純に勇者のHPか魔王のHPが0になったかどうかで判断します。
状態sについては少し考える必要があります。
攻撃力や防御力などの複数のステータスがありますが、Q学習で評価すべきステータスは「勇者のHP」と「魔王のHP」の実質2つだけです。
今回のバトル設計では、攻撃力・防御力などの数値は常に一定なので、HP以外のステータスを評価する必要がないからです。逆に言えば、バフ・デバフなどでステータスが変化する場合はそれらの情報も必要になります。
報酬rについては、「ターン終了」と「ゲーム終了」状態それぞれで評価します。
def __turn_end(self):
# 報酬を設定
self.reward = 0
# (省略)
def __game_end(self):
if self.hero.hp <= 0:
self.__save_log("\033[31m{}\033[0m".format("勇者は死んでしまった"))
self.reward = -1 # 報酬を設定
elif self.maou.hp <= 0:
self.__save_log("\033[32m{}\033[0m".format("魔王をやっつけた"))
self.reward = 1 # 報酬を設定
ターン経過による報酬は0としました。魔王を「最速で倒す」という目的を意識するなら、ターン経過での報酬を負の値にすればよいでしょう。(ただし、適切なパラメーターを設定するのは難しいですが。)
ゲーム終了時には、勇者が倒れてしまえば「-1」、魔王を倒せば「+1」の報酬を与えます。
2つ目に重要な部分は、reset()メソッドです。
# ゲームを1ターン目の状態に初期化
def reset(self):
self.__init__()
return (self.hero.hp, self.maou.hp)
単にゲームを初期化するだけのメソッドです。なお、Q学習のために初期状態を返す必要があります。
上記のstep()メソッドと合わせて、
ゲーム初期化(reset)→バトルが終了するまでターンを進める(step)→ゲーム初期化(reset)→バトルが終了するまでターンを進める(step)・・・
と、ゲームを繰り返すことで学習を進めていくことができます。
以上がQ学習をする上での、ゲームの根幹部分となります。
Q学習を実装する
エージェントクラスについて
Q学習は、エージェントクラス内で実装します。
エージェントとは、実際にゲームをするプレイヤーのようなクラスです。
エージェントはプレイヤー自身ですので、行動(攻撃か回復か)を選択したり、状態(勇者や魔王のHPなど)について知ったりすることはできますが、
ゲームの内部情報(行動順序を決める乱数など)を知ることはできません。
「行動」と、その行動によって得られた「状態」と「報酬」だけから学習を進めていくのが、
Q学習を含めた強化学習全般における基本的な理解になります。
初めに、エージェントクラスの全体を掲示しておきます。
DIV_N = 10
class Agent:
"""エージェントクラス"""
def __init__(self, epsilon=0.2):
self.epsilon = epsilon
self.Q = []
# 方策をε-greedy法で定義
def policy(self, s, actions):
if np.random.random() < self.epsilon:
# epsilonの確率でランダムに行動
return np.random.randint(len(actions))
else:
# (Qに状態sが含まれており、かつそのときの状態におけるQ値が0でなければ)
if s in self.Q and sum(self.Q[s]) != 0:
# Q値が最大となるように行動
return np.argmax(self.Q[s])
else:
return np.random.randint(len(actions))
# 状態を数値に変換する
def digitize_state(self, s):
hero_hp, maou_hp = s
# 勇者と魔王のHPをそれぞれDIV_Nで分割する
s_digitize = [np.digitize(hero_hp, np.linspace(0, dq_battle.Game.HERO_MAX_HP, DIV_N + 1)[1:-1]),
np.digitize(maou_hp, np.linspace(0, dq_battle.Game.MAOU_MAX_HP, DIV_N + 1)[1:-1])]
# DIV_Nの2乗までの状態数を返す
return s_digitize[0] + s_digitize[1]*DIV_N
# Q学習をする
def learn(self, env, actions, episode_count=1000, gamma=0.9, learning_rate=0.1):
self.Q = defaultdict(lambda: [0] * len(actions))
# episode_countの分だけバトルする
for e in range(episode_count):
# ゲーム環境をリセット
tmp_s = env.reset()
# 現在の状態を数値に変換
s = self.digitize_state(tmp_s)
done = False
# ゲームエンドになるまで行動を繰り返す
while not done:
# ε-greedy方策に従って行動を選択
a = self.policy(s, actions)
# ゲームを1ターン進め、その時の「状態、報酬、ゲームエンドかどうか」を返す
tmp_s, reward, done = env.step(a)
# 状態を数値に変換
n_state = self.digitize_state(tmp_s)
# 行動aによって得られた価値(gain) = 即時報酬 + 時間割引率 * 次の状態における最大のQ値
gain = reward + gamma * max(self.Q[n_state])
# 現在推測している(学習する前の)Q値
estimated = self.Q[s][a]
# 現在の推測値と、行動aを実行してみたときの実際の価値をもとに、Q値を更新
self.Q[s][a] += learning_rate * (gain - estimated)
# 現在の状態を次の状態へ
s = n_state
状態を数値に変換する
エージェントクラスで少しわかりにくいのは、状態を数値に変換するメソッドでしょうか。
# 状態を数値に変換する
def digitize_state(self, s):
hero_hp, maou_hp = s
# 勇者と魔王のHPをそれぞれDIV_Nに分割する
s_digitize = [np.digitize(hero_hp, np.linspace(0, dq_battle.Game.HERO_MAX_HP, DIV_N + 1)[1:-1]),
np.digitize(maou_hp, np.linspace(0, dq_battle.Game.MAOU_MAX_HP, DIV_N + 1)[1:-1])]
# DIV_Nの2乗までの状態数を返す
return s_digitize[0] + s_digitize[1]*DIV_N
先ほども軽く触れましたが、Q学習をする上で評価すべき状態変数は、「勇者のHP」と「魔王のHP」の2つです。しかし、Q学習では状態を1つの数値として表す必要があります。つまり、以下のようなイメージです。
- 状態1:(勇者のHP, 魔王のHP) = (0, 0)
- 状態2:(勇者のHP, 魔王のHP) = (0, 1)
- 状態3:(勇者のHP, 魔王のHP) = (0, 2)
上記のように変換しても良いのですが、これだとHP×HPの数だけ状態が増えることになります。ドラクエじゃない方の某国民的RPGのように、HPが4桁もあると状態数が100万を超えて大変です(笑)。ですので、HPの割合に応じて状態を分割してやることにしましょう。
np.digitize(hero_hp, np.linspace(0, dq_battle.Game.HERO_MAX_HP, DIV_N + 1)[1:-1]
このコードをざっくりと解説すると、
np.linspace()で、0から最大HPまでをN分割し、
np.digitize()で、現在のHPが、何分割目に属しているかを返すイメージです。
今回はN=10としているので、
- HPが1割未満 → 0
- HPが1割以上、2割未満 → 1
- HPが2割以上、3割未満 → 2
のように変換してくれます。更に、
「勇者の状態(0〜9)+ 魔王の状態(0〜9)*10」
の計算をすることで、0から99までの100個に状態数を抑えることができます。
状態「15」なら、魔王のHPが「1」割未満、かつ勇者のHPが「5」割未満と、直感的にわかりますね。
方策の定義
方策はε-greedyを採用しています。
# 方策をε-greedy法で定義
def policy(self, s, actions):
if np.random.random() < self.epsilon:
# epsilonの確率でランダムに行動
return np.random.randint(len(actions))
else:
# (Qに状態sが含まれており、かつそのときの状態におけるQ値が0でなければ)
if s in self.Q and sum(self.Q[s]) != 0:
# Q値が最大となるように行動
return np.argmax(self.Q[s])
else:
return np.random.randint(len(actions))
初学者の方のために簡単に解説すると、基本的には行動価値が最大となるように行動を決定し、εの確率でランダムな行動を採用する方策です。
行動にある程度のランダム性をもたせることにより、様々な行動を探索するため、Q値の初期値に依存することなく適切な学習が可能となります。
Q学習の実装
さて、ここまでくればQ学習に必要な変数・メソッドは全てそろいました。
Q学習のアルゴリズムは以下です。
- $Q(s,a)$を初期化。
- 任意の回数バトルを繰り返す:
- ゲーム環境の初期化
- ゲームエンドまでターンを進める:
- 方策$π$に従って行動$a$を選択する。
- 行動$a$を行い、報酬$r$と次の状態$s′$を観測する。
- $Q(s,a)$を以下のように更新する。
$Q(s,a)$$\leftarrow$$Q(s,a)+α(r+γ*$$\underset{a′}{max}$$Q(s′,a′)−Q(s,a))$ - $s$$\leftarrow$$s′$とする。
記事の冒頭でも述べたとおり、Q学習の理論については解説しませんので、上記のアルゴリズムを素直に実装しましょう。
# Q学習をする
def learn(self, env, actions, episode_count=1000, gamma=0.9, learning_rate=0.1):
self.Q = defaultdict(lambda: [0] * len(actions))
# episode_countの分だけバトルする
for e in range(episode_count):
# ゲーム環境をリセット
tmp_s = env.reset()
# 現在の状態を数値に変換
s = self.digitize_state(tmp_s)
done = False
# ゲームエンドになるまで行動を繰り返す
while not done:
# ε-greedy方策に従って行動を選択
a = self.policy(s, actions)
# ゲームを1ターン進め、その時の「状態、報酬、ゲームエンドかどうか」を返す
tmp_s, reward, done = env.step(a)
# 状態を数値に変換
n_state = self.digitize_state(tmp_s)
# 行動aによって得られた価値(gain) = 即時報酬 + 時間割引率 * 次の状態における最大のQ値
gain = reward + gamma * max(self.Q[n_state])
# 現在推測している(学習する前の)Q値
estimated = self.Q[s][a]
# 現在の推測値と、行動aを実行してみたときの実際の価値をもとに、Q値を更新
self.Q[s][a] += learning_rate * (gain - estimated)
# 現在の状態を次の状態へ
s = n_state
これで、ゲームとQ学習の実装までが完了しました。
ゲームを実行&学習
ランダムに行動させてみる
Q学習をする前に、勇者の行動をランダムにしてバトルするとどうなるのか試してみましょう。
以下のコードを追加します。
class Agent:
# (省略)
# テストバトル
def test_run(self, env, actions, draw=True, episode_count=1000):
turn_num = 0 # 撃破ターン数
win_num = 0 # 勝数
# episode_countの分だけバトルする
for e in range(episode_count):
tmp_s = env.reset()
s = self.digitize_state(tmp_s)
done = False
while not done:
a = self.policy(s, actions)
n_state, _, done = env.step(a)
s = self.digitize_state(n_state)
if draw:
env.draw() # バトルログを描画
if env.maou.hp <= 0:
win_num += 1
turn_num += env.turn
# 平均勝率・平均撃破ターン数を出力
if not win_num == 0:
print("平均勝率{:.2f}%".format(win_num*100/episode_count))
print("平均撃破ターン数:{:.2f}".format(turn_num / win_num))
else:
print("平均勝率0%")
if __name__ == "__main__":
game = dq_battle.Game()
agent = Agent()
actions = dq_battle.Character.ACTIONS
""" 完全ランダムでバトル """
agent.epsilon = 1.0
agent.test_run(game, actions, episode_count=1000)
ε=1.0とすることで、100%完全ランダムで行動させています。
また、1000回のバトル結果から、平均勝率・平均撃破ターン数を計算するようにしてみました。
以下、実行結果です。
$ python q-learning.py
平均勝率0.90%
平均撃破ターン数:64.89
勝率はかなり低いですね…。
ターン数を見ればわかるように、長期戦になりやすい傾向があります。
長期戦になればなるほど勇者が瀕死の状態が増えるので、その結果勝ちにくくなることが予想されます。
Q学習後にバトルさせてみる
以下のコードを追加します。
if __name__ == "__main__":
# (省略)
""" Q学習する """
agent.epsilon = 0.2
agent.learn(game, actions, episode_count=1000)
""" テストバトル """
agent.epsilon = 0
agent.test_run(game, actions, episode_count=1000)
ε=0.2とし、Q学習を実行してみます。
その後、1000回のテストバトルを行います。
なお、ε=0(0%ランダム)にすることで、学習した行動価値の通りに行動させています。
以下、学習するバトル数を変えて実行結果を示します。
実行結果(学習バトル数:50、テストバトル数:1000)
$ python q-learning.py
平均勝率42.60%
平均撃破ターン数:56.19
実行結果(学習バトル数500、テストバトル数:1000)
$ python q-learning.py
平均勝率100.00%
平均撃破ターン数:55.00
実行結果(学習バトル数5000、テストバトル数:1000)
$ python q-learning.py
平均勝率100.00%
平均撃破ターン数:54.00
勝率100%になりましたね!
学習後のQ値ってどうなってるの?
少しだけ考察をしてみます。
学習した結果のQ値を見てみましょう。
以下、バトル数1000で学習させてみたときのQ値を、一部の状態について抜き出しました。
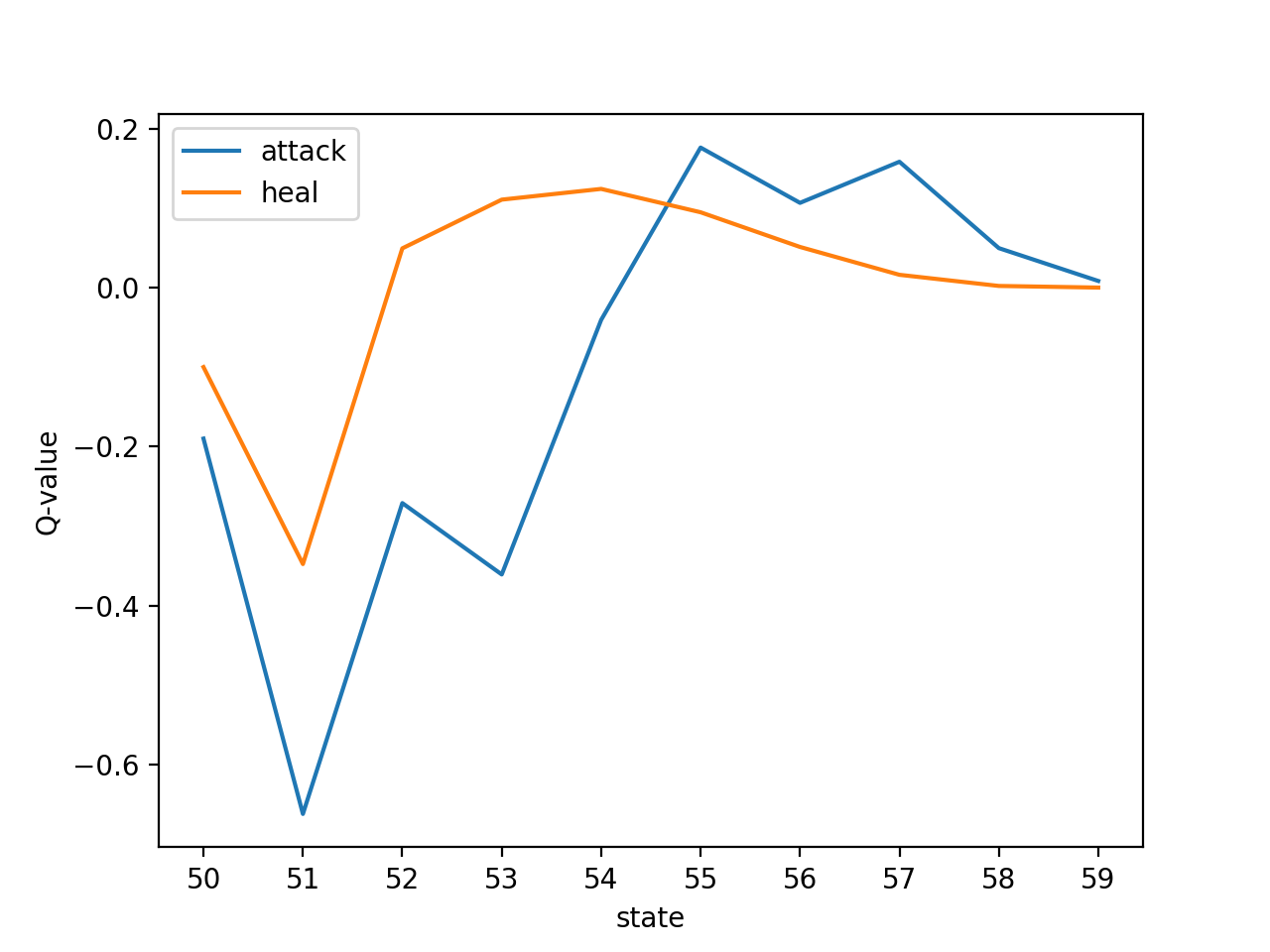
状態50:[-0.19, -0.1]
状態51:[-0.6623164987957537, -0.34788781183605283]
状態52:[-0.2711479211007827, 0.04936802595531123]
状態53:[-0.36097806076138395, 0.11066249745943924]
状態54:[-0.04065992616558749, 0.12416469852733954]
状態55:[0.17619052640036173, 0.09475948937059306]
状態56:[0.10659739434775867, 0.05112985778828942]
状態57:[0.1583472103200607, 0.016092008419030468]
状態58:[0.04964633744625512, 0.0020759614034820224]
状態59:[0.008345513895442138, 0.0]
状態の見方は、10の位が魔王の残りHP、1の位が勇者の残りHPです。
つまり上記の図は、魔王の残りHPが5割程度のとき、勇者の残りHPによって行動価値がどう変化するかを表現した図になります。
図から、勇者の残りHP(1の位)が低ければ「回復」コマンド、残りHPが高ければ「攻撃」コマンドを選択していることが読み取れます。
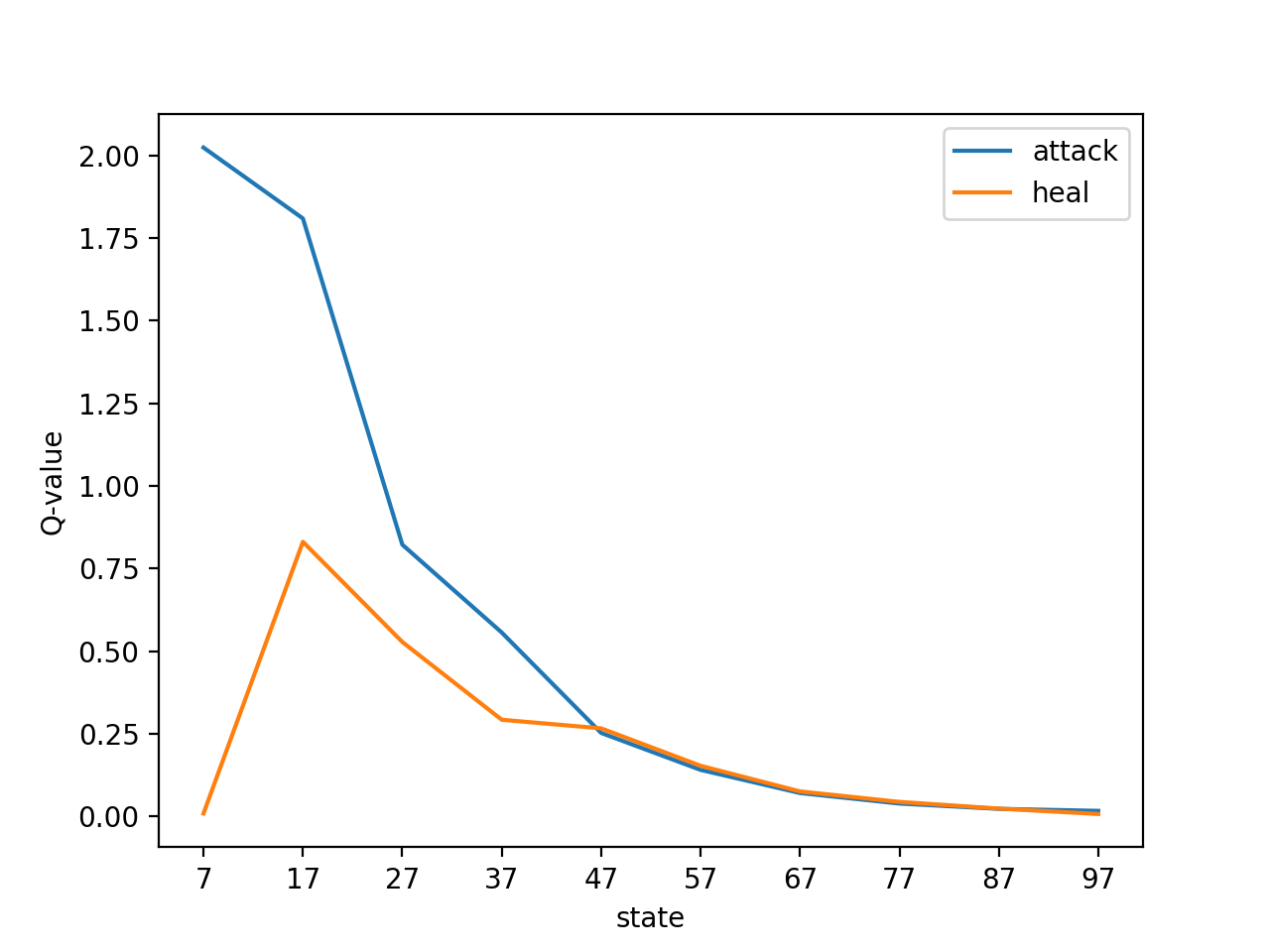
状態07:[2.023809062133135, 0.009000000000000001]
状態17:[1.8092946131557912, 0.8310497919226313]
状態27:[0.8223927076749513, 0.5279685031058523]
状態37:[0.5565475393122992, 0.29257906153106145]
状態47:[0.25272081107828437, 0.26657637207739293]
状態57:[0.14094053800308323, 0.1533527340827757]
状態67:[0.0709128688771915, 0.07570873469406877]
状態77:[0.039059851207044236, 0.04408123679644829]
状態87:[0.023028972190011696, 0.02386492692407677]
状態97:[0.016992303227705185, 0.0075795064515745995]
上図は、勇者の残りHPが7割程度のとき、魔王の残りHPによって行動価値がどう変化するかを表現しています。
魔王の残りHPが少ないほど「攻撃」優位になっていることが読み取れると思います。
最後に
本記事は実装がメインなので、その他考察などは省略します。
余裕のある方は、ハイパーパラメータを変えて学習してみたり、バトルルールをより複雑にすることに挑戦してみると面白いでしょう。
また、筆者は強化学習初心者ですので、間違い等ありましたらお気軽にご指摘ください。
筆者の知識も強化されて嬉しくなります。
ソースはgithubにおいています。
https://github.com/nanoseeing/DQ_Q-learning