ESIMアルゴリズムの解説と実装

下記論文のアルゴリズム解説と実装です．

Title: Enhanced LSTM for Natural Language Inference
Author: Chen, et al.
Year: 2017
URL: https://arxiv.org/abs/1609.06038

どういうお話かというと，２つの文書がどういった関係になっているのか(例: 前提と仮説，同じ意味かどうかなど)を求めるアルゴリズムにDecomsable Attentionがあって，その改良版であるESIMの性能が良いらしいので，Kerasで実装してみたよという話です．

また，下記事はこのアルゴリズムの前身となったDecomposable Attentionについてです．

Decomposable Attentionアルゴリズムの解説と実装

ESIMとは

• ESIMはEnhanced Sequential Inference Modelの略でDecomposable Attention¹の改良版
• 2つの文書を入力とするクラス分類用のアルゴリズム
• KaggleのQuora²優勝者も利用．(単一モデルでは一番性能が良かったとのこと)

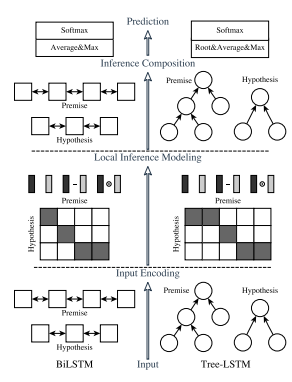
アルゴリズムの全体(原論文³より引用)

Decomposable Attentionとの違い

• Tree-LSTM⁴を使う．(BiLSTM⁵でも可)
• Compare時に差分や要素積を使う．
• Aggregation時にMax PoolingだけでなくAverage Poolingも使う．

アルゴリズム

❏流れ

Decomposable Attentionと流れ自体は同じ．

• Attend(整列)
  • 比較しやすくするために似た意味の単語が同じような場所に並ぶよう整列．
• Compare(比較)
  • 並べたベクトルを比較して2つの特徴ベクトルに変換
• Aggregate(集約)
  • 2つの特徴ベクトルを結合させてクラスごとの尤度を算出

❏入力変数

入力の文書$a$,文書$b$はそれぞれ$l_a$,$l_b$の長さの単語で構成されていて，各要素は分散表現(例: GloVe⁶やWord2Vec⁷)によって$d$次元のベクトルに変換されているものとします．

a = (a_1, ..., a_{l_a})^\mathrm{T} \\
b = (b_1, ..., b_{l_b})^\mathrm{T} \\

単語を分散表現に変換(実験では300次元のGloVe⁶を使用)

\bar{a}_i = \mathrm{BiLSTM}(a, i),\quad \forall i \in \left\{1,...,l_a\right\} \\
\bar{b}_j = \mathrm{BiLSTM}(b, j),\quad \forall j \in \left\{1,...,l_b\right\} \\

❏Attend

ここはDecomposable Attentionと一緒．

\begin{align}
e_{ij} &= \bar{a}_i^\mathrm{T}\bar{b}_j　\\
\tilde{a}_i &= \sum_{j=1}^{l_b} \frac{\exp(e_{ij})}{\sum_{k=1}^{l_a}\exp(e_{kj})} \bar{b}_j, \quad \forall i \in \left\{1,...,l_a\right\} \\
\tilde{b}_j &= \sum_{i=1}^{l_a} \frac{\exp(e_{ij})}{\sum_{k=1}^{l_b}\exp(e_{ik})} \bar{a}_i, \quad \forall j \in \left\{1,...,l_b\right\}  \\
\end{align}

何をやっているのかというと，

• A). 私 は りんご を 焼いて 食べた
• B). 昨日 みかん を 僕 は 食べた

という２つの文章があったときに

$\bar{a}$	私	は	りんご	を	焼いて	食べた
$\tilde{a}$	僕	は	みかん	を	-	食べた

と似たような要素がペアになるよう並び替えたほうが，比較しやすくなるので，
２つの文章に関係のありそうな単語に重みを付けて文書を整列させてりしてる．
(実際にはベクトル同士の計算)

❏Compare

\begin{align}
m_a &= (\bar{a}, \tilde{a}, \bar{a}-\tilde{a}, \bar{a} \odot \tilde{a})^\mathrm{T} \\
m_b &= (\bar{b}, \tilde{b}, \bar{b}-\tilde{b}, \bar{b} \odot \tilde{b})^\mathrm{T} \\
\end{align}

Decomposable Attentionでは$\bar{a}, \tilde{a}, \bar{b}, \tilde{b}$の２つのみだったが，ESIMでは減算や要素積も追加することで性能を上げている模様．

❏Aggregate

v_{a,t} = \mathrm{BiLSTM}(F(m_a)) \\
v_{b,t} = \mathrm{BiLSTM}(F(m_b))

ここで原論文ではTreeLSTM⁴とBiLSTM⁵の両方を方式を提案しているが，本記事では実装の都合もありBiLSTMを用いています．
また関数$F$はフィードフォワードニューラルネット．

v_{a,\mathrm{ave}} = \sum_{i=1}^{l_a}\frac{v_{a,i}}{l_a}, \quad 
v_{a,\max} = \max_{i=\left\{1,..l_a\right\}}\frac{v_{a,i}}{l_a}, \\

v_{b,\mathrm{ave}} = \sum_{j=1}^{l_b}\frac{v_{b,i}}{l_b}, \quad 
v_{b,\max} = \max_{j=\left\{1,..l_b\right\}}\frac{v_{b,j}}{l_b}, \\

v = (v_{a,\mathrm{ave}}, v_{a,\max}, v_{b,\mathrm{ave}}, v_{b,\max})^\mathrm{T}

Decomposable Attentionだと$\max$だけだったが調整しづらいので，$\mathrm{avg}$もつけたとのこと．

実装

コード⁸を参考にしています．

References

1. Parikh, A Decomposable Attention for Natural Language Inference, 2016. (Decomposable Attentionの原論文) ↩

2. Maximilien@DAMI, Quora Question Pairs - 1st place solution, 2017. (Kaggle-Quora優勝者の記事) ↩

3. Chen, Enhanced LSTM for Natural Language Inference, 2017. (ESIMアルゴリズムの原論文) ↩

4. Tai et al., Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks, 2015. (木構造でのLSTM) ↩ ↩²

5. Bahdanau, Neural machine translation by jointly learning to align and translate, 2014. (機械翻訳の論文, BiLSTMについて言及) ↩ ↩²

6. Pennington et al., Glove: Global vectors for word representation., 2014. (分散表現アルゴリズムGloVeの原論文) ↩ ↩²

7. Milkolov et al., Efficient Estimation of Word Representations in Vector Space, 2013. (分散表現アルゴリズムWord2Vecの元論文) ↩

8. Dang, Quora Question Pairs - DL models, 2017. (ESIMとDecomposable Attentionのコードあり) ↩