Decomposable Attentionアルゴリズムの解説と実装

下記論文のアルゴリズム解説と実装です．

• Title: A Decomposable Attention Model for Natural Language Inference
• Author: Ankur P.Parikh, et al.
• Year: 2016
• URL: https://arxiv.org/abs/1606.01933

どういう話かというと，前提と仮定， 受け答え，既出のネタかどうかなど２つの文章の関係を調べたいときに，Decomposable Attention¹アルゴリズムが使えそうなので，どうやって性能を改善しているのかを紹介しつつ，Kerasで実装してみた²という話です．

Decomposable Attention¹とは

• 自然言語推論(Natural Language Inference: NLI)用のネットワーク
• 2つの文書を入力とするクラス分類問題に利用
• Attention¹をネットワークに組み込むことで従来より性能を改善
• KaggleのQuora Question Pairs^3で優勝者³も利用

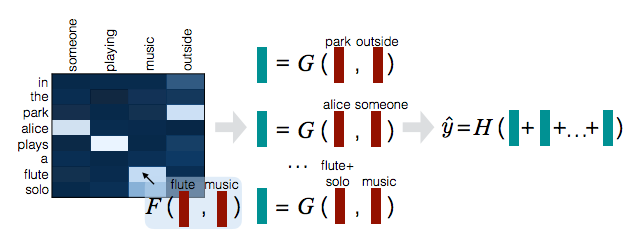
図: A Decomposable Attention for Natural Language Inference¹より

アルゴリズム

このアルゴリズムを利用するためには各単語をGloVe⁴やWord2Vec⁵で分散表現に変換しておく必要があります．

❏ 流れ

• Attend(整列?)
  • 互いの文書に関係のある単語ほど重みを高くつつ並び替える．
• Compare(比較)
  • 整列させた二文を比較し，2つの特徴ベクトルに変換
• Aggregate(集約)
  • 特徴ベクトル同士を結合させクラスごとの尤度を算出

❏ 入力変数

入力文章のペアを

\bar{a} = (a_1, ..., a_{l_a})^\mathrm{T} \\
\bar{b} = (b_1, ..., b_{l_b})^\mathrm{T} \\

とする．ここで$l_a, l_b$は文書の長さを表す．

また，$a_i,b_j\in \mathbb{R}^d$は何らかの分散表現したもの．

• 実験ではGloVe⁴で300次元の分散ベクトルに変換
• 分散ベクトル$\bar{a},\bar{b}$は$1$の$l_2$ノルムに正規化

❏ Attend

attentionの重みは下記で計算．こうすることで，重要な単語同士は相関が高くなるように並び替える．

e_{ij} := F'(\bar{a_i}, \bar{b_j}) := F(\bar{a})^{\mathrm{T}}F(\bar{b})

とする．このattentionの重み$e_{ij}$によって文書$a$と$b$の関係の深い単語同士は重みが強くなるようになる．

実装時の関数$F$は単なるニューラルネットワーク．

$F'$で計算してしまうと，入力変数の次元が$l_a \times l_b$となり大きいので，
実際に計算する際には$l_a + l_b$の入力次元数で$F$と簡略化している．

この$F$は実装時は全結合のニューラルネットワーク．

計算したattentionの重み$e_{ij}$をもとに$\bar{a_i},\bar{b_j}$を正規化した値$\alpha_i, \beta_j$を求める．

\beta_i := \sum_{j=1}^{l_b} \frac{ \exp(e_{ij}) }{ \sum_{k=1}^{l_b} \exp(e_{ik})} \bar{b}_j \quad \forall i \in \left\{1,...,l_a \right\} \\

\alpha_j := \sum_{i=1}^{l_a} \frac{ \exp(e_{ij}) }{ \sum_{k=1}^{l_b} \exp(e_{kj})} \bar{a}_j \quad \forall j \in \left\{1,...,l_b \right\} 

❏ Compare

v_{1,i} := G([\bar{\alpha_i}, \beta_i]) \quad \forall i \in \left\{1,...,l_a \right\} \\
v_{2,j} := G([\bar{\beta_j}, \alpha_i]) \quad \forall j \in \left\{1,...,l_b \right\}

ここで$G$は実装時にはニューラルネットワーク．

❏ Aggregate

v_1 = \sum_{i=1}^{l_a} v_{1,i} \\
v_2 = \sum_{j=1}^{l_b} v_{2,j} \\
\hat{y} = H([v_1, v_2])

❏ Intra-Sentence Attention(任意)

単語埋め込み部分で，単に単語ごとに変換するのではなくニューラルネットを使うことで文としての意味も取り込めるのではないかと考えた機能．

f_{ij} := F_{\rm{intra}}(a_i)^{\mathrm{T}}F_{\rm{intra}}(a_j)

ここで，$F_{\rm{intra}}$はフィードフォワードネットとして，$\bar{a_i},\bar{b_i}$を以下に変更にする．

\bar{a_i} := [a_i, a'_i]\\
\bar{b_i} := [b_i, b'_i]

ここで，$a'_i$は

a'_i := \sum_{j=1}^{l_a} \frac{\exp(f_{ij} + d_{i-j})}{\sum_{k=1}^{l_a} \exp(f_{ik + d_{i-k}})} a_j

としています．この$d_{i-j} \in \mathbb{R}$はバイアス． $b'_i$についても同様

実装²

コード^{6 7 8}を参考にKeras⁹で作成しています．

References

1. Parikh, A Decomposable Attention for Natural Language Inference, 2016. ↩ ↩² ↩³ ↩⁴

2. namakemono, Decomposable Attention with Keras, 2017. ↩ ↩²

3. Maximilien@DAMI, Quora Question Pairs - 1st place solution, 2017. ↩

4. Pennington et al., Glove: Global vectors for word representation., 2014. ↩ ↩²

5. Milkolov et al., Efficient Estimation of Word Representations in Vector Space, 2013. ↩

6. Dang, Quora Question Pairs - DL models, 2017. ↩

7. explosion, spaCy, 2017. ↩

8. lystdo, LSTM with word2vec embeddings, 2017. ↩

9. Chollet, Keras, 2016. ↩