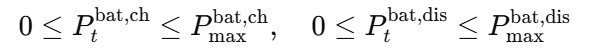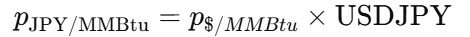【数理最適化】発電上限やコストを決める

この記事は「【リアルタイム電力予測】需要・価格・電源最適化ダッシュボード構築記」シリーズの十五日目です
Day1はこちら | 全体構成を見る

前回は、変数・目的関数・制約を設定しました。
ただし、まだ「上限やコストをいくらにするか」という 定数 を決めていませんでした。
今回は、どのように定数を設計するか（= 上限・容量・コストの決め方）がテーマです。

1. 上限やコストの定数

1.1 定数によってどのような影響があるか

• 上限を大きく取りすぎると
  • 「そんなに出ないはずの電源」がフル稼働してしまう
  • 予備力制約が形骸化する
• 上限を小さく取りすぎると
  • 無駄に需給遮断や高コスト電源が動員される

⇒ つまり、物理的・運用的な根拠を持って上限を決めないと、最適化が現実から乖離してしまうということです。
ただし東京エリアの「厳密な設備容量」を私が網羅的に把握するのは難しいため、今回は 実績ベースで上限を更新する方針を取ります（＝データドリブンで現実に寄せるイメージです）。

1.2 長期と短期で考える

上限の決め方を次の2つに分けます。

• 長期的な上限（構造的上限）：その季節・設備として「通常ここまでは出る（出ている）」
• 短期的な上限（運用上限）：直近の運用状況として「最近この程度までしか出ていない」

⇒ 一日の上限は両者の小さい方を採用し、突発要因（故障・点検・燃料制約）にも寄せられるようにします。

2. 今回決めていく定数

最適化に必要な以下を設計します。

• 太陽光・風力の時刻別上限
• 火力・水力などの設備容量（出力上限）
• 水力の一日エネルギー予算
• 蓄電池・揚水の容量（出力上限・エネルギー容量・効率・初期残量）
• 連系線（受電）の上限
• 燃料コスト（円/MWh）

3. 太陽光・風力の上限

火力や水力は「設備があれば出せる」電源である一方、太陽光・風力は 「設備があっても天気次第で出せない」電源 です。そのため、以下のように上限の推定方法を変えてみます。

• 火力・水力：出力そのものに上限を課す
• 太陽光・風力：
  1. 今日使える設備容量（CAP） を実績から推定
  2. 気象から時刻別の稼働率（CF） を作る
  3. $Avail_t=CAP_{today}×CF_t$ で時刻別上限を作る

3.1 設備容量（CAP）の推定（PV/Wind）

CAPは、長期と短期を組み合わせます。

• 長期上限（構造）：過去の「日次最大」の高分位点（例：99.5%）にマージン
• 短期上限（運用）：直近X日の「日次最大」の最大値にマージン（例：α=1.05）
• 今日の上限：両者の小さい方
  イメージとしては次の式です。
  

安全策として、実績が欠損した日や0になる日については、以下のようにフォールバックを入れます。

• 直近最大が 0 または欠損 → 前日の CAP を採用
• 前日の CAP も無い → 長期 CAP を採用
• 上記のいずれも無い → 初期値（固定の暫定値）を採用

3.2 太陽光の時刻別稼働率

気象情報から時刻別の稼働率を作ります。

太陽光

太陽光は、短波放射（W/m²）から稼働率を作ります。

• 入力：shortwave_radiation（短波放射, W/m²）
• 基準放射: g_stc =1000 W/m²
• パフォーマンス比: PV_PR=0.85
  　太陽光パネルに理論上入る日射量と現実の発電量の比率
  　参考：太陽光発電の「PR値」って何？〜発電効率を見える化する、重要な健康指標〜

⇒ 日射量をその日の最大値で正規化し、PRを掛ける

def pv_capacity_factor_stc(
    shortwave_radiation_wm2: pd.Series,
    pv_pr: float = PV_PR,
    g_stc: float = G_STC,
) -> pd.Series:
    """
    太陽光の稼働率（0〜1）を、STC（標準試験条件）ベースの簡易式で作る
    """
    G = shortwave_radiation_wm2.astype(float).clip(lower=0.0)
    cf_raw = (G / float(g_stc)) * float(pv_pr)
    return cf_raw.clip(lower=0.0, upper=1.0)

def make_pv_avail(weather, cap_mw: float = PV_CAP_INIT_MW,):

    cf = pv_capacity_factor_stc(weather["shortwave_radiation"], pv_pr=PV_PR, g_stc=G_STC)
    out = pd.DataFrame({
        "timestamp": weather["timestamp"],
        "pv_cf": cf.astype(float),
        "pv_avail_MW": (float(cap_mw) * cf.astype(float)),
    })
    return out[["timestamp", "pv_avail_MW"]]

※太陽光発電はPhotovoltaic、略してPVとしています

3.3 風力の時刻別稼働率

風力は、10m風速からハブ高へ補正し、パワーカーブで稼働率を作ります。

• 入力：wind_speed_10m

(1) ハブ高補正（べき法則）

• ハブ高: HUB_HEIGHT=100
• ALPHA=0.14
  　風速は高さによって変わります。地表10mの風速$v$からタービンのハブ高$h$での風速を推定するときにはべき法則が使われます。
  参考：NEDO>NeoWins(洋上風況マップ)

大気中の風速の高さ方向の分布（鉛直）は地表面の凸凹の大きさ（地表面粗度）によって異なり、風速は上空に行けば行くほど大きくなり、一般的にべき法則で表すことができます。これは、風速の大きさは地上高さのべき乗に比例するというもので、べき指数αを用いて表されます。一般的にべき指数αは0.1～0.3の値をとります。地表面付近で風速が減速するのは、地表面の凸凹による摩擦力のためで、海面のような滑らかな表面では、摩擦力が小さいためべき指数αは小さく（0.1～0.14）、陸上において凸凹が大きくなる（平野・草原→森林・住宅地→大都市・複雑地形）に従い摩擦力が大きいためαは大きな値（0.14～0.3）となります。

(2) パワーカーブ

• 3 m/s 未満：発電しない（安全上停止）
• 3〜12 m/s：立ち上がり領域（立方則で増加）
• 12〜25 m/s：定格出力（一定出力）
• 25 m/s 以上：危険なので停止
  ⇒上記のパワーカーブを以下のようパラメータとして設定します
• V_CUT_IN = 3 m/s
• V_RATED = 12 m/s
• V_CUTOUT = 25 m/s

上記のキャパシティファクタを掛けます。

def wind_capacity_factor_power_curve(v_hub: np.ndarray) -> np.ndarray:
    """
    風力の簡易パワーカーブ（稼働率 0〜1）。
    - v < cut-in: 0
    - cut-in <= v < rated: 立ち上がり（ここでは3乗で近似）
    - rated <= v < cut-out: 1
    - v >= cut-out: 0（安全停止）
    """
    cf = np.zeros_like(v_hub, dtype=float)

    mask1 = (v_hub >= V_CUT_IN) & (v_hub < V_RATED)
    mask2 = (v_hub >= V_RATED) & (v_hub < V_CUTOUT)

    # ratedに向かって滑らかに増える近似：((v - cut_in)/(rated - cut_in))^3
    cf[mask1] = ((v_hub[mask1] - V_CUT_IN) / (V_RATED - V_CUT_IN)) ** 3
    cf[mask2] = 1.0
    # cut-out以上は 0 のまま
    return np.clip(cf, 0.0, 1.0)

def make_wind_avail(weather, cap_mw: float = WIND_CAP_INIT_MW,):
    """
    weather から 風力の時刻別上限（wind_avail_MW）を作る
    """
    v10 = weather["wind_speed"].astype(float).to_numpy()
    v_hub = v10 * (HUB_HEIGHT / 10.0) ** ALPHA

    cf = wind_capacity_factor_power_curve(v_hub)

    out = pd.DataFrame({
        "timestamp": weather["timestamp"],
        "wind_cf": cf.astype(float),
        "wind_avail_MW": (float(cap_mw) * cf.astype(float)),
    })
    return out[["timestamp", "wind_avail_MW"]]

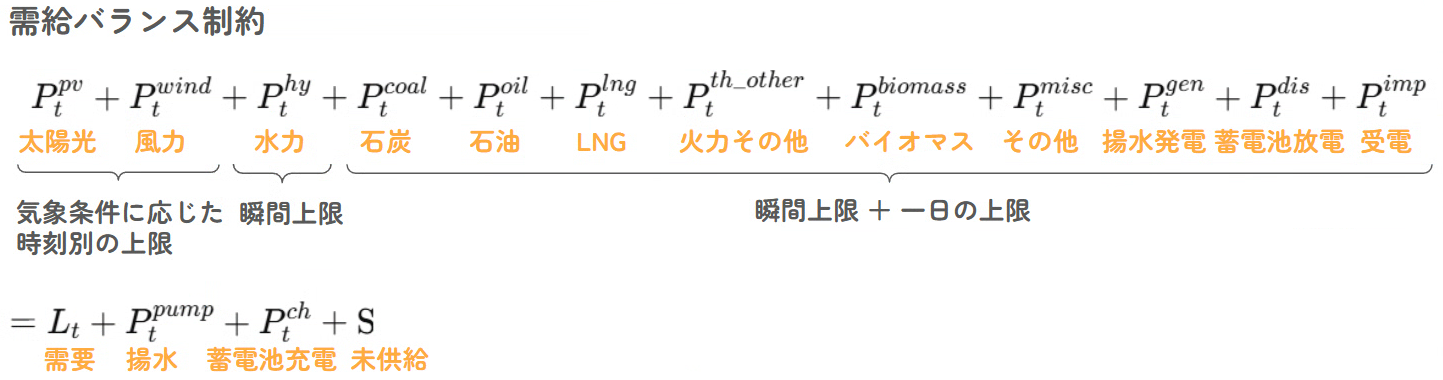
4 火力・水力などの設備容量（出力上限）

設備があれば出力できる電源の上限を扱います。

• 火力（LNG/石炭/石油/火力その他）
• 水力（通常水力）
• バイオマス
• その他（VPP 等）
• 連系線（受電上限）
• ※蓄電池の放電上限、揚水の発電上限も「出力上限」という意味では同じ枠に入ります

火力や水力では、理論上の設備容量があっても故障、定期点検、燃料制約、運用上の都合によって、その日使える上限が変動します。
そのためここもPV/Windと同じく、実績から長期＋短期で上限を推定し、毎日更新します。

4.1 長期上限

過去一定期間の実績からピーク分位点を取ります。

• $Q_q$：q分位点（例：q=0.995）
• margin：安全側に持つための倍率（例：1.05）

def estimate_pmax_long_term(series, long_conf, stat):
    """
    過去全期間の実績（30分値）から、「構造的な上限」を推定
    - stat: 
        - "quantile": 日次最大の分布の上側分位点（例：0.995）× margin
        - "avg":      日次最大の平均 × avg_margin（ベースロード系向けに使う想定）
    """

    if series is None or series.empty:
        return np.nan
    if not isinstance(series.index, pd.DatetimeIndex):
        raise ValueError("series.index must be DatetimeIndex")
    
    daily_max = series.resample("1D").max()
    if daily_max.empty:
        return np.nan

    if stat == "avg":
        mean_val = float(daily_max.mean())
        margin = float(long_conf.get("avg_margin", 1.0))
        return mean_val * margin

    q = float(long_conf.get("quantile", 0.995))
    margin = float(long_conf.get("margin", 1.05))
    ref = float(daily_max.quantile(q))
    return ref * margin

4.2 短期上限（直近の上限）

直近x日の最大値に倍率を掛けます。

def recent_max(series: pd.Series, today: pd.Timestamp, recent_days: int = 7) -> float:
    """
    直近 recent_days 日の 1日最大値のうち最大を返す。
    series: 30分値などの時系列（DatetimeIndex）
    today: 今日（例: 2025-12-13）
    """
    if series is None or series.empty:
        return np.nan
    if not isinstance(series.index, pd.DatetimeIndex):
        raise ValueError("series.index must be DatetimeIndex")

    start = pd.Timestamp(today) - pd.Timedelta(days=int(recent_days))
    end = pd.Timestamp(today) + pd.Timedelta(days=1)

    s = series.loc[(series.index >= start) & (series.index < end)]
    if s.empty:
        return np.nan

    daily_max = s.resample("1D").max()
    if daily_max.empty:
        return np.nan

    return float(daily_max.max())

⇒ これらを今日の上限を以下のとおり定義します。

ここでも実績ができない場合は0になってしまうので以下のようなルールを設けます。

• 短期推定が 0/欠損 → 前日の上限を採用
• 前日の上限も無い → 長期上限を採用
• 長期上限も無い → 初期値（params.yaml の暫定値）を採用

def effective_pmax(series, long_conf, short_conf, today, stat, fallback_prev_cap=None, fallback_init_cap=None):
    """
    - 長期 + 直近を組み合わせた「今日の P_max」を計算
    - base = 長期構造的上限
    - recent_cap = 直近の最大出力 * alpha
    - → P_max_today = min(base, recent_cap)
    """
    base = estimate_pmax_long_term(
        series,
        long_conf=long_conf,
        stat=stat
    )
    print("base: \n", base)
    
    recent_days = int(short_conf.get("recent_days", 7))
    rmax = recent_max(series, today, recent_days=recent_days)
    print("rmax: \n", rmax)
    if rmax is None:
        return base
    recent_cap = rmax * float(short_conf.get("alpha", 1.05))
    
    # recent_cap が使えない場合（欠損 or ほぼ0）
    min_valid = float(short_conf.get("min_valid", 1e-6))
    if pd.isna(recent_cap) or recent_cap <= min_valid:
        if fallback_prev_cap is not None and fallback_prev_cap > min_valid:
            return float(fallback_prev_cap)
        if not pd.isna(base) and base > min_valid:
            return float(base)
        if fallback_init_cap is not None and fallback_init_cap > min_valid:
            return float(fallback_init_cap)
        return 0.0

    # base が欠損なら recent を採用
    if pd.isna(base) or base <= min_valid:
        return float(recent_cap)

    return float(min(base, recent_cap))

5. 水力の一日エネルギー予算

水力は「瞬間の出力上限（MW）」だけでなく、「一日に使える水量（= エネルギー量, MWh）」が効きます。
そこで日次エネルギー制約を置きます。

• $T_d$：その日の時刻集合（48スロット）
• $\Delta t$：0.5h
  

考え方は火力に日次上限も組み合わさったイメージです。

• 火力：瞬間上限（MW）が主
• 水力：瞬間上限（MW）＋日次上限（MWh）が効く

6. 蓄電池・揚水

蓄電池と揚水は「時間をまたいで電力を移動させる」設備です。
「電力（MW）」と「残量（MWh）」を分けて考えます。
また、予備力制約のために上げ幅（今すぐ増やせる余力）を表す変数も入れています。

6.1 蓄電池

(1) 変数

• 放電電力（MW）$P_t^{bat,ch}≥0$
• 放電電力（MW）$P_t^{bat,dis}≥0$
• 残量（MWh）$E_t^{bat}≥0$
• 放電側の予備力（MW）$R_t^{bat}≥0$

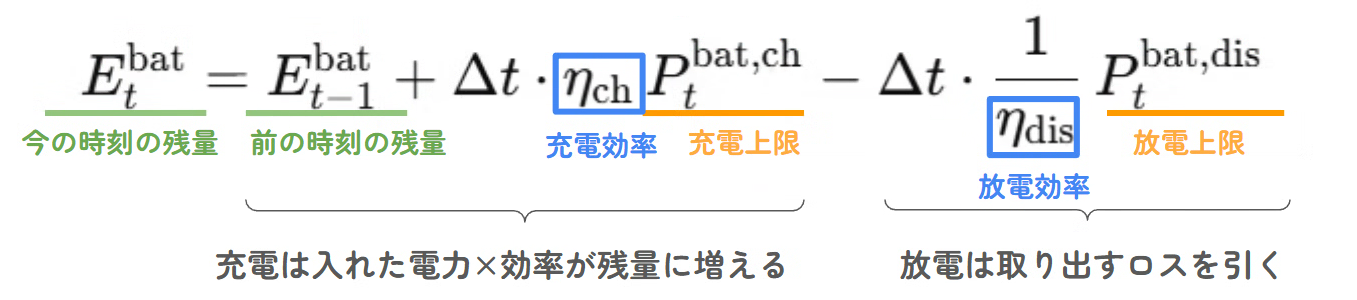
(2) エネルギーバランス

残量を以下のように考えます。

• 充電は「入れた分のうち効率ぶんだけ増える」
• 放電は「同じ電力を出すのに、残量からは効率の逆数ぶん減る」
• $E_t^{bat}$は中に残っているエネルギー（MWh）で$P_t^{bat,dis}$は系統へ出す電力（MW）→単位が違うので必ず$△t$をかけてMWをMWhに変換する

(3) 容量制約

• 残量（エネルギー容量）
  
• 充電・放電の出力上限（MW）
  

上記の定数を以下のように設定しました。

• $E_{\max}$（容量）は 固定
• $P^{\text{dis}}_{\max}$（放電上限）は 実績から動的推定（effective_pmax） して更新
• $P^{\text{ch}}_{\max}$（充電上限）は、実績から動的推定（effective_pmax） して更新

(4) 予備力（上げ幅）の制約

• 放電出力の余力で縛る
  放電出力の上限まであとどれだけ上げられるかを示す
  

• 残量（エネルギー）で縛る
  そもそも残量が足りないと上げられないことを示す
  

6.2 揚水

揚水発電も蓄電池と同じ構造です（水をくみ上げる＝充電、水を落とす＝放電）

(1) 変数

• 揚水（ポンプ）（MW）$P_t^{ps,pump}≥0$
• 揚水（発電）電力（MW）$P_t^{ps,gen}≥0$
• 上池相当の残量（MWh）$E_t^{ps}≥0$
• 発電側の予備力（MW）$R_t^{ps}≥0$

(2) エネルギーバランス

(3) 容量制約

• 残量（MWh）
  

• 揚水（ポンプ）・発電（MW）
  

こちらも蓄電池と同様に定数を置いていきます。

• $E^{\text{ps}}_{\max}$ は固定
• $P^{\text{ps,gen}}_{\max}$（発電上限）は実績から動的推定して更新（effective_pmax）
• $P^{\text{ps,pump}}_{\max}$（揚水上限）は実績から動的推定して更新（effective_pmax）

予備力の制約

蓄電池と同様に2本の制約を入れています。

7. 連系線の受電

今回は需要不足を埋める用途に限定しているので、受電（輸入）のみを考えています。

(1) 変数

• 受電電力（MW）$P_t^{imp}≥0$
• 受電の予備力（MW）$R_t^{imp}≥0$

(2) 容量（上限）と予備力（上げ幅）

こちらも今までと同様に実績から動的推定して更新するようにしています。
​

「今の受電＋上げ幅が上限以内」としています。

8. 燃料コスト（可変費）

最適化の目的関数に入れたいのは、各火力の 可変費（円/MWh） です。
そして最適化モデル側では、30分値の発電量（MW）を使うので、MWhに直すためにΔtを掛けます。
ここではコストを示す$c$を作っていきます。

8.1 市場価格を $/MMBtu に揃える

原油は「1バレルあたり約 5.8 MMBtu」という関係、石炭についても「1トン（※短トン）あたり約24 MMBtu」程度の換算を用います。※実際には炭種や単位で変わります

• 原油（Brent）：/bbl→/MMBtu
  
• 石炭（一般炭）: /t→/MMBtu
  
• LNG: 取得元であるHenry Hubの値を/MMBtuとみなしてそのまま使用

8.2 為替を掛けて 円/MMBtu にする

8.3 熱量単価を「電力量単価」に変換（× HEATRATE）

HEATRATEは電気1MWhを作るのに必要な燃料（MMBtu）の量を表します。

HEATRATE = {  # MMBtu/MWh
    "lng": 6.5,
    "coal": 9.0,
    "oil": 10.0,
}

これは、以下の資料にあるモデルプラントの効率から逆算した値です。

参考：資源エネルギー庁>発電コスト検証WG[火力発電]

⇒ここでようやく「電気1MWhを作る燃料費（円/MWh）」になります

8.4 可変O&M と CO₂コストを足す

• $VOM_f$: 可変O&M（円/MWh）
  燃料費とは別に、発電量に比例して増加する運転・保守費用を近似したものです。
  実際の発電コスト分解では、燃料費が支配的であり、VOMはその1割未満となるケースが多いため、本モデルでは数百〜千円/MWh 程度のオーダーで設定しています。
  電源ごとの差については、
  • LNG：燃焼がクリーンで灰処理が不要
  • 石炭：灰処理・脱硫脱硝設備の運転が必要
  • 石油：起動停止が多く設備負担が大きい
    といった運用・設備特性を反映し、LNG < 石炭 < 石油 の関係となるように設定しています。

VOM_YEN_PER_MWH = {
    "lng": 500.0,
    "coal": 1000.0,
    "oil": 1200.0,
}

• $EF_f$: 排出係数（t-CO2/MWh）
  LNG < 石油 < 石炭になるようにしています。

CO2_T_PER_MWH = {
    "lng": 0.35,
    "coal": 0.90,
    "oil": 0.75,
}

• $CO2Price$: 円/t-CO2
  日本では明確な炭素価格がありません。社会的コストを内部化するための擬似的な炭素価格として扱っています。
  2022年に開設された東証のカーボンクレジット市場において、1tあたり3,000円くらいで取引価格となっています。※2024年6月以降は再エネに分類されるクレジットにおいては6,000円を超えるケースも出てきています

CO2_PRICE_YEN_PER_T: float = 3000.0

• 「燃料費＋可変O&M＋CO₂コスト」までまとめたものを、発電の世界では 可変費（variable cost） と呼びます

すべて合わせた関数：

def make_fuel_cost(market):
    """
    市場データ（1日分）から、火力の可変費（円/MWh）を作る
    - 1) 商品価格を $/MMBtu に寄せる（単位変換）
    - 2) USDJPY を掛けて 円/MMBtu にする
    - 3) (円/MMBtu × heatrate) + 可変O&M + CO2コスト を足して 円/MWh にする
    変換の前提：
    - 原油: 1 bbl ≒ 5.8 MMBtu
    - 一般炭: 1 t ≒ 24 MMBtu
    - LNG: Henry Hub を $/MMBtu としてそのまま
    """

    # $/MMBtu への変換
    market["oil_usd_per_mmbtu"]  = market["brent"].astype(float) / 5.8
    market["coal_usd_per_mmbtu"] = market["coal_aus"].astype(float) / 24.0
    market["lng_usd_per_mmbtu"]  = market["henry_hub"].astype(float)

    # 円/MMBtu（為替掛け）
    fx = market["USDJPY"].astype(float)
    market["oil_jpy_per_mmbtu"]  = market["oil_usd_per_mmbtu"]  * fx
    market["coal_jpy_per_mmbtu"] = market["coal_usd_per_mmbtu"] * fx
    market["lng_jpy_per_mmbtu"]  = market["lng_usd_per_mmbtu"]  * fx

    def varcost_yen_per_mwh(row: pd.Series, fuel: Literal["lng", "coal", "oil"]) -> float:
        fuel_jpy_per_mmbtu = float(row[f"{fuel}_jpy_per_mmbtu"])
        return (
            fuel_jpy_per_mmbtu * float(HEATRATE[fuel])
            + float(VOM_YEN_PER_MWH[fuel])
            + float(CO2_PRICE_YEN_PER_T) * float(CO2_T_PER_MWH[fuel])
        )

    market["c_lng"]  = market.apply(varcost_yen_per_mwh, axis=1, fuel="lng")
    market["c_coal"] = market.apply(varcost_yen_per_mwh, axis=1, fuel="coal")
    market["c_oil"]  = market.apply(varcost_yen_per_mwh, axis=1, fuel="oil")

    return market[["timestamp", "c_coal", "c_oil", "c_lng"]]

まとめ

最終的な需給バランス制約は以下のようになります。

明日

今日までで、変数、制約、定数の設定ができました。明日は実際に最適化モデルに入力してみます！