この記事は「【リアルタイム電力予測】需要・価格・電源最適化ダッシュボード構築記」シリーズの十四日目です
Day1はこちら | 全体構成を見る
前回は、電力システムにおける数理最適化とは何か、どのような問題が現実に解かれているのかを整理しました。
今回は実際に 「経済負荷配分問題」 をどのような変数・目的関数・制約で表現するかを数式レベルで整理していきます。
0. 今回扱う最適化問題の整理
まず、取り扱う問題をもう一度整理します。
使用するcsvはこちら：
区別しやすいように名前を変えます。
name_map = {
"thermal_lng": "lng",
"thermal_coal": "coal",
"thermal_oil": "oil",
"thermal_other": "th_other",
"hydro": "hydro",
"pumped_hydro": "pstorage", # 正：プラス発電、マイナス揚水
"battery": "battery", # プラス放電、マイナス充電
"interconnection": "tie",
"nuclear": "nuclear",
"geothermal": "geothermal",
"biomass": "biomass",
"other": "misc",
"solar": "pv",
"wind": "wind",
}
actual.rename(columns=name_map, inplace=True)
actual.set_index("timestamp", inplace=True)
actual.head()
扱う問題：経済負荷配分問題（Economic Dispatch）
- いつ・どの電源を・どれだけ動かすか
- 需要を満たしつつ、トータルのコスト（燃料費＋ペナルティ）を最小にしたい
という問題です。
1. 意思決定変数（Decision Variables）
各時刻における各電源の発電量や、連系線・蓄電池・揚水発電に関する「出力・エネルギー残量」を決めます。
2. 目的関数（Objective）
- 一日の総コスト（燃料費＋各種ペナルティ）を最小化します
今回は燃料コストのみを扱い、実務上重要な「起動停止コスト」「CO₂コスト」などは簡略化のため除いています<(_ _)>
3. 制約条件（Constraints）
- 需要＝供給（需給バランス）
- 各電源の出力上限・下限
- 予備力（リザーブ）の確保
- ランプ制約（火力・水力の変化速度制限）
- 水力・蓄電池・揚水のエネルギーバランス
- 連系線の容量制約
これらを一つずつ数式で書き下していきます！
1. 前提
1.1 電源の種別
今回扱う主な電源は次のとおりです。
- 太陽光：
pv - 風力：
wind - 水力：
hydro - 火力（LNG, 石炭, 石油, 火力その他）：
lng,coal,oil,th_other - バイオマス：
biomass - その他（VPP 等）：
misc - 連系線：
tie - 蓄電池：
battery - 揚水発電：
pstorage
最適化の「通常の発電機」グループを次の集合で表します。
$$
\mathcal{G} = {\text{pv}, \text{wind}, \text{hydro}, \text{coal}, \text{oil}, \text{lng}, \text{th_other}, \text{biomass}, \text{misc}}
$$
※ 連系線・蓄電池・揚水発電は振る舞いが特殊なので、ここでは別扱いとします。
1.2 時刻の集合
30分刻みの時刻スロット：
$$
t \in \mathcal{T}
$$
1 スロットあたりの時間幅：
$$
\Delta t = 0.5 \ \text{[hour]}
$$
1.3 需要
時刻 $t$ の需要（負荷）：
$$
L_t \ \text{[MW]}
$$
1.4 予備力
安定供給のためには、一定以上の予備力を持つことが求められます。ここでは予備率 $\rho$ を用いて必要予備力を以下のように定義します。
$$
R^{\text{req}}_t = \rho , L_t
$$
参考：資源エネルギー庁>政策について>電力・ガス>電力需給対策>ディマンド・リスポンス（DR）>電力需給状況
2. 変数（意思決定変数）
2.1 各電源の発電量
各時刻 $t$ における各電源の発電出力（MW）を変数にします。
火力（LNG・石炭・石油・火力その他）
$$
P^{\text{lng}}_t \ge 0,\quad
P^{\text{coal}}_t \ge 0,\quad
P^{\text{oil}}_t \ge 0,\quad
P^{\text{th_other}}_t \ge 0
$$
太陽光・風力
$$
P^{\text{pv}}_t \ge 0,\quad
P^{\text{wind}}_t \ge 0
$$
水力
$$
P^{\text{hydro}}_t \ge 0
$$
バイオマス・その他
$$
P^{\text{biomass}}_t \ge 0,\quad
P^{\text{misc}}_t \ge 0
$$
2.2 太陽光・風力の出力抑制量
天候次第でポテンシャルは変わりますが、系統の状況によっては発電を「絞る（カットする）」必要があります。その「捨てた分」を以下のように定義します。
- 太陽光の出力抑制量
$$
C^{\text{pv}}_t \ge 0
$$ - 風力の出力抑制量
$$
C^{\text{wind}}_t \ge 0
$$
後で、この量にペナルティを課すことで「できるだけ捨てたくない」ことをモデルに反映させることが狙いです。
2.3 需給遮断量（停電量）
需要をすべて満たせないとき、「何 MW 分を諦めたか（停電したか）」を以下で表します。
$$
S_t \ge 0
$$
停電はあってはならないので、この変数に非常に大きなペナルティ単価を設定することで、どうしても他に手段がない場合だけ選ばれるようにします。
2.4 連系線（受電／送電）
エリア間での電力のやり取りを次のように分けます。
- 受電（他エリアからの輸入）
$$
P^{\text{imp}}_t \ge 0
$$ - 送電（他エリアへの輸出）
$$
P^{\text{exp}}_t \ge 0
$$
便宜上、連系線のネット潮流を以下のように定義します。
$$
P^{\text{tie}}_t = P^{\text{imp}}_t - P^{\text{exp}}_t
$$
2.5 蓄電池
蓄電池は「電力（瞬間の入出力）」と「エネルギー（残量）」を分けて考えます。
- 充電電力（系統から蓄電池へ）：
$$
P^{\text{bat,ch}}_t \ge 0
$$ - 放電電力（蓄電池から系統へ）：
$$
P^{\text{bat,dis}}_t \ge 0
$$ - 蓄電池のエネルギー（残量）：
$$
E^{\text{bat}}_t \ge 0
$$
2.6 揚水発電
揚水発電も同様に、「ポンプで水をくみ上げるとき」と「水を落として発電するとき」に分けて考えます。
- 揚水（ポンプ消費側）：
$$
P^{\text{ps,pump}}_t \ge 0
$$ - 揚水（発電側）：
$$
P^{\text{ps,gen}}_t \ge 0
$$ - 貯水池のエネルギー（有効落差×水量を電力量換算したもの）：
$$
E^{\text{ps}}_t \ge 0
$$
揚水発電は「電力の需要側」として振る舞うとき（ポンプ）と、「発電側」として振る舞うときがあり、蓄電池とほぼ同じ役割を果たします。
3. 目的関数
一日の総コストを最小化することが目的です。
$$
\min Z
= \sum_{t \in \mathcal{T}} \Delta t \left(
\text{FuelCost}_t + \text{Penalty}_t
\right)
$$
3.1 燃料コスト
自然エネルギーである水力・太陽光・風力は、ここでは「燃料費 0 円」とみなします。燃料費を持つ電源の単価を
- LNG 単価：$c^{\text{lng}}$ [円/MWh]
- 石炭単価：$c^{\text{coal}}$
- 石油単価：$c^{\text{oil}}$
- 火力その他単価：$c^{\text{th_other}}$
- バイオマス単価：$c^{\text{biomass}}$
- その他単価：$c^{\text{misc}}$
とすると、時刻 $t$ の燃料コストは
となります。
3.2 ペナルティ・受電コスト
ペナルティや連系線コストも目的関数に含めます。
- 太陽光出力抑制ペナルティ単価：
$$
\pi^{\text{pv}}_{\text{curtail}} \ [\text{円/MWh}]
$$ - 風力出力抑制ペナルティ単価：
$$
\pi^{\text{wind}}_{\text{curtail}}
$$ - 需給遮断ペナルティ単価（非常に大きい）：
$$
\pi^{\text{shed}}
$$ - 連系線からの受電コスト（輸入単価）：
$$
c^{\text{imp}}
$$
とすると、時刻 $t$ のペナルティ・輸入コストは以下のようになります。
4. 制約条件
4.1 需給バランス制約
「発電＋受電＋蓄電池・揚水の放電」が、「需要＋揚水ポンプ＋蓄電池の充電＋需給遮断」と一致するようにします。
左辺が系統に「入ってくる電力」、右辺が系統から「消費される電力」です。
4.2 発電上限・下限制約
各電源には「設備容量（最大出力）」があります。電源 $g \in \mathcal{G}$ に対する時刻 $t$ の上限を $\overline{P}^g_t$ とすると、
$$
0 \le P^g_t \le \overline{P}^g_t
\qquad (\forall g \in \mathcal{G},\ \forall t)
$$
となります。
太陽光・風力の $\overline{P}^g_t$ は時刻により変化し、水力や火力などは当日一定とする予定です。
この上限をどう推定するかは、次回の記事で詳しく説明します。
4.3 予備力制約
各時刻 $t$ において、「まだ使っていない余力の合計」が必要予備力以上になるようにします。
火力・水力・連系線など、調整可能な電源集合を $\mathcal{G}_{\text{flex}}$ とすると、余力は「上限−現在出力」で表せるので
と書けます。
4.4 ランプ制約（火力・水力）
火力や水力は、1 スロットで急激に出力を変えることができません。
電源 $g$ の上昇ランプ（1 ステップで上げられる最大量）を $RU^g$、下降ランプを $RD^g$ とすると、$t>t_0$ について
となります。
この制約によって、時間変化がなめらかな出力パターンになります。
4.5 水力の一日エネルギー予算
水力発電には「一日に使える水量の上限」があります。これがないと、安いからといって水力を出しっぱなしにしてしまいます。
一日に使える水力エネルギーの上限を $E^{\text{hydro}}_{\text{day,max}}$ とすると以下のように表します。
4.6 蓄電池のエネルギーバランスと容量制約
蓄電池の残量は「前時刻の残量＋充電−放電」で決まります。
- 充放電効率をそれぞれ $\eta_{\text{ch}}, \eta_{\text{dis}}$ とすると蓄電池のエネルギーバランスは以下のようになります
- 容量上限 $E^{\text{bat}}_{\max}$ を用いると、容量制約は以下のようになります
4.7 揚水発電のエネルギーバランス
揚水発電の貯水池も同様に、時間をまたいでエネルギー保存の式が必要です。
- ポンプ効率：$\eta_{\text{pump}}$
- 発電効率：$\eta_{\text{gen}}$
-
エネルギーバランス
-
容量制約は以下のようになります
4.8 連系線の上限制約
連系線にも系統計画で決まっている容量上限があります。
片方向の上限を $P^{\text{tie}}_{\max}$ とすると、以下のように表されます。
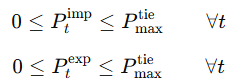
5. まとめ
今回は、経済負荷配分問題 を扱います
- 変数（各電源の発電量・蓄電池・揚水・連系線など）
- 目的関数（燃料費＋ペナルティの合計）
- 制約条件（需給バランス・上限下限・予備力・ランプ制約・エネルギーバランス）
を数式として定義しました。
明日
各電源の出力上限 $\overline{P}^g_t$ をどのように推定・設定するか について、実データ（過去実績や予測値）を使った具体的な方法を考えます！