【リアルタイム電力予測】需要・価格・電源最適化ダッシュボード構築記 Advent Calendar 2025

【電力価格予測】分位点回帰（理論編）

Last updated at 2025-12-08Posted at 2025-12-08

この記事は「【リアルタイム電力予測】需要・価格・電源最適化ダッシュボード構築記」シリーズの九日目です
Day1はこちら | 全体構成を見る

前回は電力価格データの特徴について可視化し、電力価格がどのような要因で変動するのかを整理しました。
今回からはいよいよ予測モデルの理論編に入り、なぜ平均回帰ではなく分位点回帰（Quantile Regression）を採用するのかを説明していきます。

電力価格データの復習

電力価格は、

長期トレンド（燃料価格・為替レート）
短期トレンド（気温・需要・再エネ発電量）
周期性（季節・時間帯・曜日）

といった複数の要因が複雑に絡み合って決まります。

こちらは季節別に時間帯の平均価格を描画したものです。
季節ごとに平均の形そのものが大きく異なることが分かります。

季節ごとで平均の形が大きく異なることが分かります。

冬（紫）
- 早朝から価格が高く、夕方にかけて急騰します
  -暖房負荷や日照不足の影響で、高価格帯に分布が偏る傾向があります
夏（赤）
- 午前中は太陽光で価格が抑えられやすい一方、午後の気温上昇で価格が跳ね上がります
- 太陽光が強く発電する日は、低価格に張り付くケースも多く見られます
  → 高価格と低価格の両極端が出やすく、分布が広いことが特徴です
春・秋（黄・青）
- 気温が穏やかで需要ピークが小さく、全体として安定しています
- 価格分布も比較的狭く、平均が代表性を持ちやすい季節です

このように季節ごとに価格分布が大きく異なり、分散が多く外れ値が頻出してしまいます。

分布のゆがみ

例として、17時の電力価格ヒストグラムを描いてみると、次のようになります。

ヒストグラムを見ると、右側に長い裾を持つ右に歪んだ分布になっていることが分かります。
こうした分布では、100円・200円台といった極端に高いスパイク価格が少数ながら存在するため、平均値が大きく引き上げられてしまいます。
図でも示すように、

中央値（赤線）＝13.11円
平均値（青線）＝17.73円

となっており、平均値がスパイクに引っ張られて上昇してしまっています。

続いて、時間帯ごとの分散を見てみます。

もっとも分散が大きいのは夕方の17時で、気象・需要・再エネ条件が複雑に重なる時間帯です。
このように、ばらつきが大きいため、平均予測だけでは構造をうまく表現できないことが分かります。

平均（最小二乗法）が抱える問題

平均回帰では、損失関数に MSE（平均二乗誤差）を用います。

スパイクが1点あるだけで、平均が強く引き上げられることになります
MSEは外れ値に非常に敏感で、スパイクに過剰に引っ張られる

その結果として、通常時の予測精度が悪くなることにつながります。
このように、電力価格のように歪み・裾の長さ・外れ値が多いデータには平均回帰が構造的に向いていません。

分位点回帰（Quantile Regression）

そこで登場するのが分位点回帰です。
分位点回帰では、価格の 代表値 そのものではなく、
「分布のどのあたりに価格が落ち着きそうか」
を直接予測します。

例として、次の3つの分位点を扱います。

10% 分位（q=0.1）
→ 太陽光が強い・需要が弱いなどの 低価格帯
50% 分位（q=0.5 中央値）
→ その時間の典型的な価格
90% 分位（q=0.9）
→ 需要ひっ迫・供給不足など 高価格帯

先ほどの分散のplotについて、分位点も描画してみました。

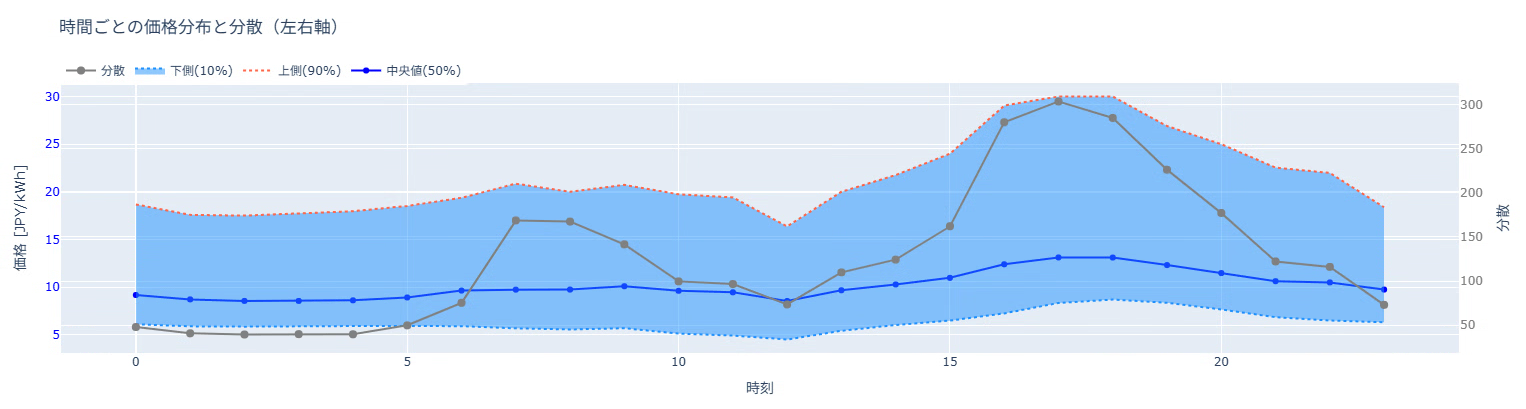
分位点レンジ（q10〜q90）をプロットした図を見ると、分散とよく連動していることが分かります。
ばらつきが大きい時間帯では分位点レンジも広がり、
逆に安定した時間帯ではレンジが狭くなります。
この「分布の幅をそのまま予測できる」という点が、分位点回帰の最大のメリットです。