この記事はfreee データに関わる人たち Advent Calendar 2019 6日目のエントリーです。
前日の夜中に書きはじめてヒーヒー言いながら書いています。
はじめに
PyClusteringというライブラリを皆さんご存知でしょうか。PyClusteringはPythonとC++から利用できるクラスタリングに特化したライブラリです。そんなPyClustering v0.9.2にG-meansというアルゴリズムが新しく実装されました。G-meansという名前を初めてみた + 日本語の記事が見当たらなかったので調べてまとめてみました。
アルゴリズム自体はシンプルなので論文を直接読んで頂くのが一番分かりやすいかも知れません。
G-means
G-meansはK-meansを拡張したものでK-meansのパラメータであったクラスタ数を自動で決定してくれるアルゴリズムです。
似たような方法にX-meansというものがありますがそちらは「クラスタ数を自動推定するX-means法を調べてみた」でコードとともにわかりやすく紹介されています。(ちなみにPyclusteringではX-meansも使えます)
アルゴリズム
アルゴリズムは以下の通りです。停止条件が違うだけで小さいクラスタ数からはじめてそれを再分割していくのはX-meansと同じですね。
- 適当にいくつか中心点を決める。
- 1.で決めた中心点を初期値として使ってK-meansによるクラスタリングを行う。
- 2.でできた各クラスタ内のサンプルに対してガウス分布に従うかの統計検定(Anderson–Darling検定)を行う。1
- 帰無仮説が棄却された場合はクラスタを2つに分割する。帰無仮説が棄却されない場合はそのクラスタを確定する。2
- クラスタが分割されなくなるまで2.から4.を繰り返す。
アルゴリズムは以上ですが, 論文では
- 4.でクラスタを分割する事になった場合の新たな中心点の決め方
- Anderson-Darling検定を行いやすくするための工夫
についても言及されています。
クラスタを分割する際の新たな中心点初期値の決め方
- クラスタ内の中心点を $\mathbf{c}$ としたとき $\mathbf{c} \pm \mathbf{m}$ の2点を新たな中心点初期値とする。
- $\mathbf{m}$ は2種類提案されている。
- ランダムに決めてしまう。
- クラスタ内サンプルに対して主成分分析を行い, 第一主成分を $\mathbf{s}$ , 主成分の固有値(主成分の分散)を $\lambda$ としたとき $\mathbf{m} = \mathbf{s} \sqrt{2 \lambda / \pi}$ とする。3
論文では2番目の主成分を使った方法を採用するとのことでしたが, Pyclusteringでは1番目の方法を採用しているように見えます。
Anderson-Darling検定を行いやすくするための工夫
クラスタリングの対象となるサンプルはそのままだと高次元で統計検定しづらいので1次元に射影します。具体的には以下のようにしてサンプル $\mathbf{x}$ を1次元の $x^{\prime}$ へ射影します。
x^{\prime} = \frac{\langle \mathbf{x}, \mathbf{v} \rangle}{\| \mathbf{v} \|^2}
ただし $\mathbf{v}$ は上記「クラスタを分割する際の新たな中心点初期値の決め方」で決めた2点をそれぞれ $\mathbf{c}_1$, $\mathbf{c}_2$ としたときの $\mathbf{c}_1$ - $\mathbf{c}_2$ です。第一主成分(広がりを持っている方向の軸)に射影してそれが正規分布に従うかを検定するということですかね。
実践
さて, アルゴリズムがわかったところで実際にPyclusteringを使ってクラスタリングを行ってみたいと思います。とりあえずこちらと同じデータを対象としてみました。
ダミーデータ生成
from sklearn.datasets import make_blobs
X, Y = make_blobs(n_samples=500,
n_features=2,
centers=8,
cluster_std=1.5,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=1)
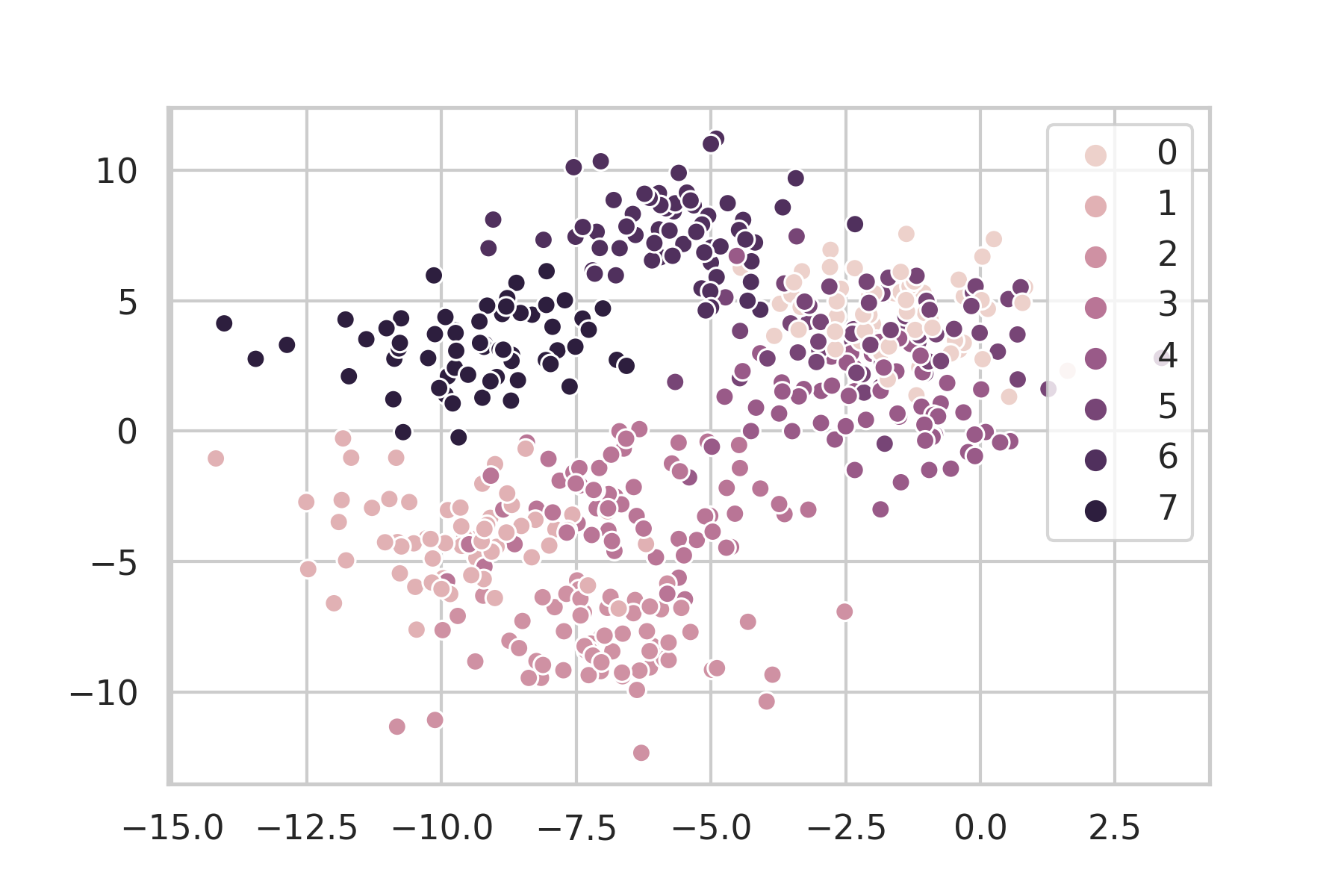
正解ラベル
正解ラベルプロット
import seaborn as sns
sns.set(style="whitegrid")
sns.scatterplot(
X[:, 0], X[:, 1], hue=Y, legend="full"
);
centers=8 なので当然8色出てきます。
G-means
さて, ここからが本題。G-meansを使ってみるとどんな感じになるのでしょうか。
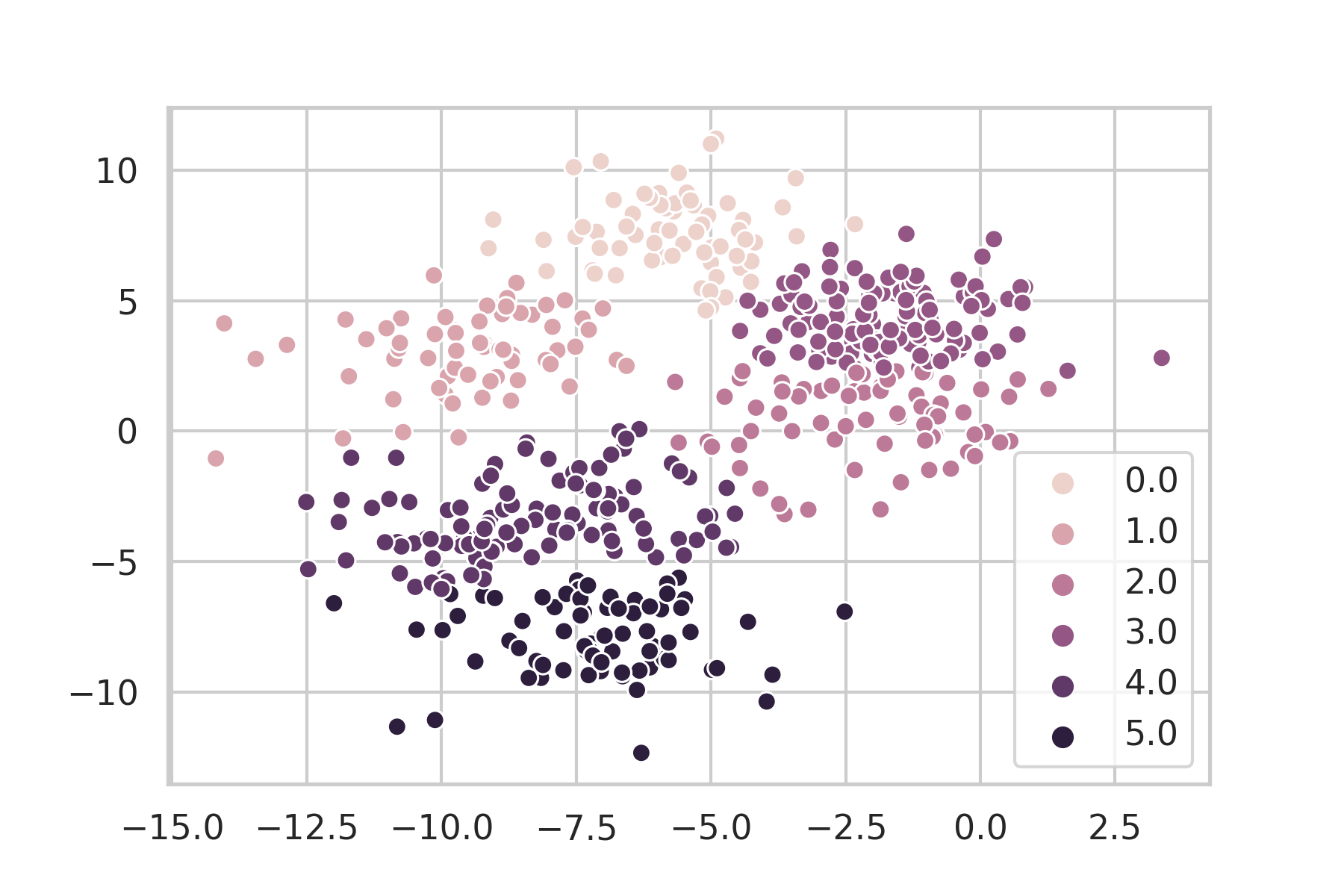
gmeans結果プロット
from pyclustering.cluster import gmeans
import numpy as np
import itertools
gmeans_instance = gmeans.gmeans(X).process()
clusters = gmeans_instance.get_clusters()
centers = gmeans_instance.get_centers()
labels_size = len(
list(itertools.chain.from_iterable(clusters))
)
labels = np.zeros((1, labels_size))
for n, n_th_cluster in np.ndenumerate(clusters):
for img_num in n_th_cluster:
labels[0][img_num] = n[0]
labels = labels.ravel()
sns.scatterplot(
X[:, 0], X[:, 1], hue=labels, legend="full"
)
おー。クラスタ数は8つではないですが違和感のない感じにクラスタリングされていますね。これは結構イケてるのではないでしょうか。
クラスタ数の見当が全くつかないような状況でクラスタをしたい場合はG-meansを使ってみると言うのはそう悪くない選択肢のように思えます。
対抗馬のX-meansは……。
最後に対抗馬としてPyclusteringのX-meansを使ってみて結果を比較したいと思います。
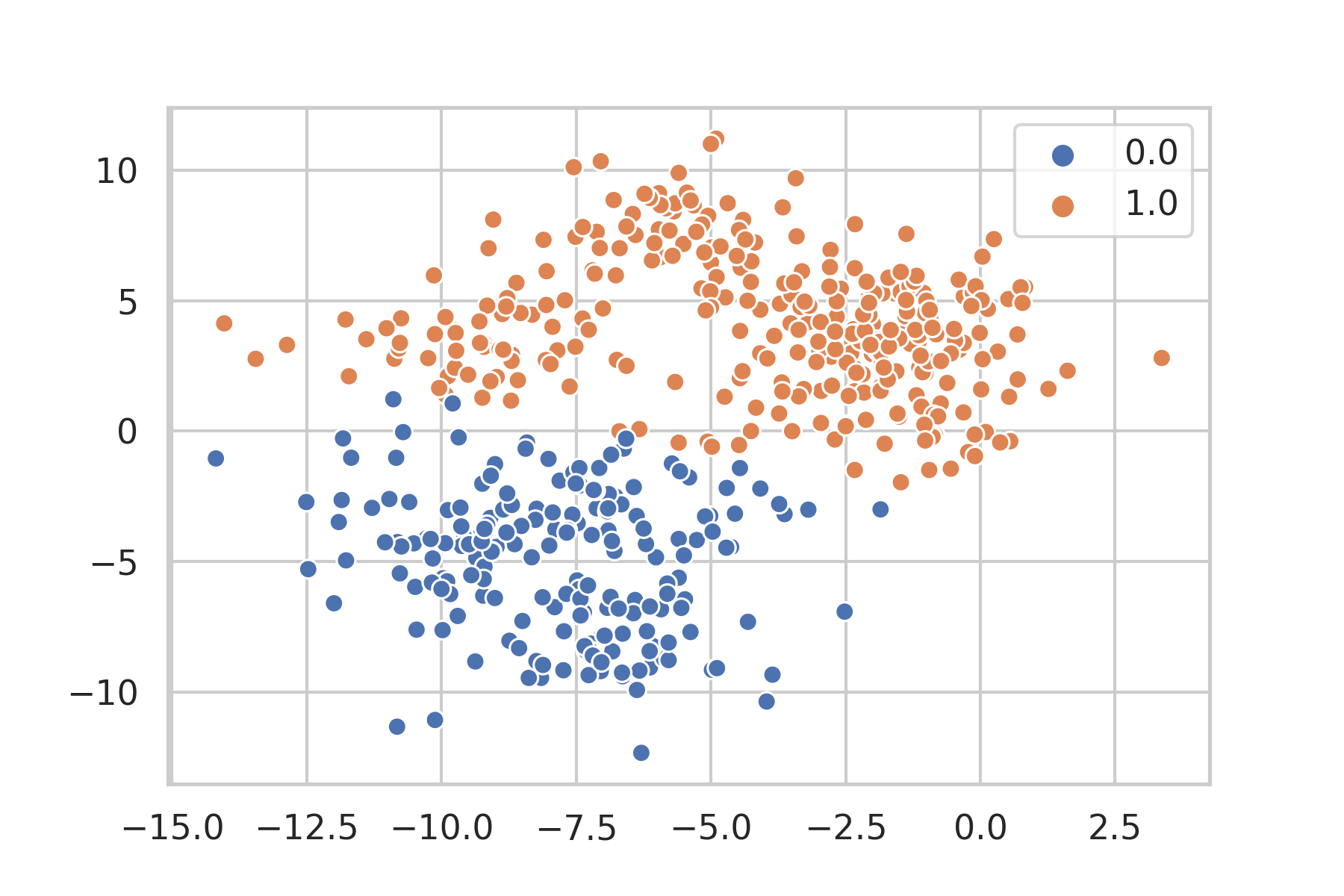
xmeans結果プロット
from pyclustering.cluster import xmeans
import numpy as np
import itertools
xmeans_instance = xmeans.xmeans(X).process()
clusters = xmeans_instance.get_clusters()
centers = xmeans_instance.get_centers()
labels_size = len(
list(itertools.chain.from_iterable(clusters))
)
labels = np.zeros((1, labels_size))
for n, n_th_cluster in np.ndenumerate(clusters):
for img_num in n_th_cluster:
labels[0][img_num] = n[0]
labels = labels.ravel()
sns.scatterplot(
X[:, 0], X[:, 1], hue=labels, legend="full"
)
あら? 参考にしたX-meansの記事とは全然違いますね……。
G-meansの論文の方にもX-meansがoverfitしてクラスタ数を過大に見積もっているという実験結果が載っているので結果に違和感が残ります……。(ここは深堀りできていない)
Pyclusteringを使う限りにおいてはX-meansよりもG-meansを使ったほうが良さそうです。
おわりに
Pyclusteringに最近(?)実装されたG-meansのアルゴリズム紹介と実際に使ってみた結果をまとめました。軽く使ってみた感じではG-meansのほうがX-meansよりも良さげな結果が得られたので「とりあえずクラスタリングしてみる!」みたいなときにはG-meansを使ってみると良いかも知れません。
ふー。Advent Calendarはなんとか間に合った……。さて寝るか……ってもう早朝じゃん!!!
-
G-meansはGaussianのGみたいですね。 ↩
-
論文では $\alpha=0.0001$ を使っていますがPyclusteringだと $\alpha=0.01$ でやっているみたいです。論文ではType I Error(偽陽性)が発生する確率を減らすようにしたほうが良いと言っているのでこの実装でいいのか?と思ってしまいます。 ↩
-
サンプルが散らばっている方向の軸を分割するとイメージでしょうか。 ↩