最初に
この記事に興味を持った人はすでにレイトレーシングとノイズについては知識を持っていると思いますので、レイトレーシングとノイズについての説明は割愛させていただきます。
その2ということで、その1を書きましたが、こちらが本当に目指していたところです。
この論文自体は、2017年のHPG(High Performance Graphics)で発表され、ベストペーパーにも選ばれた論文ですが、なんと1sppでデノイズをして、リアルタイムレイトレーシングを目指すということで、これを選んでみました。この論文は、「Edge-Avoiding A-Trous Wavelet Transform for fast Global Illumination Filtering」をベースにしています。こちらで解説しているので、そちらを先に読んでいただくといいと思います。
雑訳
雑訳とはいえ、全部を載せるのは大変なので、Introductionとコア部分である3,4章のみの超雑訳となります。
超雑訳ですので、細かいところで意味がわからない(そもそも私も理解できていない)ところもあると思いますが、ご容赦ください。
Introduction
近年、パストレース(Kajiya 1986)は、映画や視覚効果のためのレンダリングアルゴリズムとして浮上しています[Keller et al. 2015]。 これは、モンテカルロサンプリングの必然的なノイズを低減する高度なフィルタおよび再構成カーネルの開発を促進します(例えば、 Zwicker et al. [2015])。これらのカーネルは、ピクセルごとに数十から数百のサンプルでノイズフリーの画像再構成を可能にします。さらなるアルゴリズムの進歩により、パストレースされたグローバルイルミネーションへの移行は、リアルタイムグラフィックスへの兆しがあると私たちは主張します。
ビデオゲームと映画の両方が経験的モデルから物理的なシェーディングに移行しました[McAuley and Hill 2016]。しかし、ラスタライズで利用できる単純化されたライトトランスポートは開発者を正確な影、反射、multi-bounce global illuminationについて考えさせ続けます。しかし、現在のレイトレーシングのパフォーマンスは約200~300 Mrays/secに制限され[Binder and Keller 2016; Wald et al. 2014]、1920×1080および30Hzの環境ではピクセルあたりわずかなレイを与えるだけです。この数は、動的なacceleration structures、大きなシーン、および可変CPU / GPUパフォーマンスを使用したプロダクション使用ではさらに低くなります。
したがって、1パス当たりの複数のレイ、およびより高い解像度およびリフレッシュレートに対する傾向により、現実的な性能は、予測可能な将来の1ピクセル当たり1つのパスを超える可能性は低くなります。Reconstruction filterを開発することによって この制約に配慮するフィルタを使用することで、リアルタイムパストレースをより早期に実現することを目指しています。
階層的なウェーブレットベースの再構成フィルタを拡張して、拡散的で光沢のある相互反射を含む時間的に安定したグローバルイルミネーション、ソフトシャドウを1ピクセルあたり1パスのストリームから出力します。非常に低いサンプリングレートでの再構成には多くの課題があります。 貧弱なサンプリングからの高い分散は、高周波信号を不明瞭にし、1つのサンプルだけで、ノイズ源を区別することは困難です。例えば、高周波のsurfaceテクスチャを空間的にサンプリングすることによるノイズは、light transportおよび可視性によって導入される分散と融合します。
リアルタイムのパフォーマンス目標を前提としたこのフィルタは、前のフレームのサンプルを活用して、アニメーションシーンのコンテキストでも詳細なノイズを分離し、ノイズ源を切り離すのに役立ちます。1920×1080で、現在のGPUで約10ミリ秒で動作することで、将来のリアルタイムパストレースされたグローバルイルミネーションのための扉を開きます。
論文のポイントは以下となります。
-
空間的および時間的領域における推定分散によって導かれるフィルタの組み合わせを使用して構築された、1パス/ピクセル入力からの実時間再構成のための効率的かつ時間的に安定したアルゴリズム。
-
過去のフレームからの情報を使用してピクセルごとの分散推定値を計算することで、空間的な不一致を見積もり、時間方向の情報不足でも動作するようにする。
-
以前の作業(Dammertz et al. [Dammertz et al。2010])に基づいて構築され、複数のウェーブレット反復によって入力カラーをフィルタリングする空間パス。 私たちの空間パスは、時間的な分散の推定を使用して開始しますが、各反復中に更新して信頼性を向上させます。
-
新しい、シーンに依存しない幾何学的なエッジストップ機能。
我々のフィルタはシーンに依存するパラメータや基本的な光輸送アルゴリズムの知識を必要としない一方で、ノイズのないG-バッファの入力を仮定しています。つまり、被写界深度やモーションブラーといった確率的サンプリングをサポートしていません。しかし今日のゲームでは、ポスト処理を用いてこれらの効果を近似しています。
3. RECONSTRUCTION PIPELINE
ここからは、ラスタライズとパストレース入力、コンポーネントを分離してノイズ源を分離する方法、再構成フィルタ、および後処理ステップを含む、再構築パイプライン(図2参照)の概要を示します。4章では、再構成アルゴリズムのコアをより詳細にカバーします。
図2
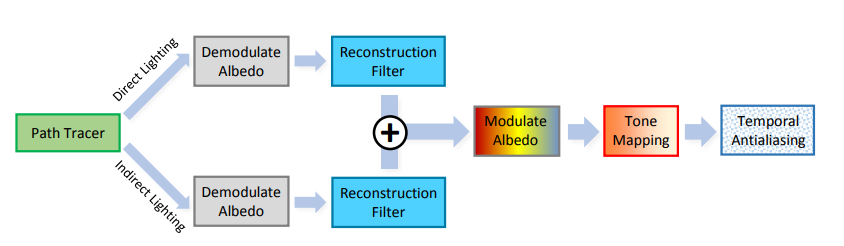
直接照明と間接照明を別々に再構成します。再構成の前に、surface アルベドは、ラスタ化されたGバッファに基づいて復調されます。これは、高周波テクスチャの細部をノイズ除去するのではなく、光輸送に関する再構築に焦点を当てています。フィルタリングの後、我々は直接的および間接的な光を一次アルベドと再結合させ、トーンマッピングおよびtemporalアンチエイリアスを適用します。
Path Tracing
再構成フィルタへの入力として、標準的なnext event estimationパストレースを使用して1 sppのカラーサンプルを生成します。私たちのパストレーサーは既存のGPUリソースをより効率的に使う最適化を含みます。それは効率的にprimary raysを生成するためのラスタライザの使用を含みます。これにより、我々の再構成フィルタを導き出すために使用される付加的な表面属性(surface attributes)を含むノイズのないGバッファ[Saito and Takahashi 1990]が提供されます(4章を参照)。
低食い違い量列のHalton列を使っています。私たちのtemporal filterの指数移動平均(exponential moving average)は数フレーム後に早いフレームでのサンプルからの寄与を失うので、小さいセットのHalton列(例、16)を利用しています。
パスの最初の散乱後のNone-diffuseの表面にはpath space regularizationを適用します[Kaplanyan and Dachsbacher 2013]。path space regularizationは本質的に増加する2次散乱事象におけるsurface roughness、high-glossyのマテリアルであっても、光源に接続することにより、パストレーサが間接的な(indirect)バウンスの寄与を見出すことを可能にします。これにより、光輸送のロバスト性が高まり、パスがより均一に寄与することが可能になります。
2回目以降のバウンスではパスごとにパスの長さを制限することで、計算コストを制限します。1つのレイが可視サーフェースにヒットしたときには、そこから2つのシャドウレイをライトにつなげます。
私たちのパストレーサは直接照明と間接照明を別々に出力します。これにより、フィルタは、両方のコンポーネントで局所的な滑らかさを個別に説明することができ、サンプリングされていないシャドウエッジの再構成が良好になります。分離はコストを倍増させるように見えますが、多くのステップがラスタライズされたGバッファを使用するため、重要な作業は共有されます。
Reconstruction
我々はまず、サンプルカラーから直接見えるsurfaceのアルベド(テクスチャおよび空間的に変化するBRDFを含む)を復調します。これにより、高周波テクスチャの詳細がぼやけてしまうのを防ぐフィルタが不要になります。
言い換えると、未処理の照明成分をフィルタリングし、再構成後にテクスチャリングを再適用します。フィルタがテクスチャの詳細をぼかしすぎないようにする必要がないことに加えて、これはまた、近隣のサンプルに対して可能な空間再利用を増加させる。Multi layer materialの場合、各レイヤーごとのアルベドをサンプリング確率で重み付けして追加します。
Reconstructionは主に3つのステップで実行されます。
- 有効なサンプリングレートを増加させるために、1パスのパストレースされた入力を時間的に蓄積します。
- これらの時間的に拡張されたカラーサンプルを使用して局所的な輝度の分散を推定します。
- これらの分散推定値を使用して 階層的なA-trousウェーブレット・フィルタを駆動します。
図3は概要を示し、第4章はこれらの手順を詳細に示します。 再構成後、surfaceアルベドを用いてフィルタ出力を(再)変調します。
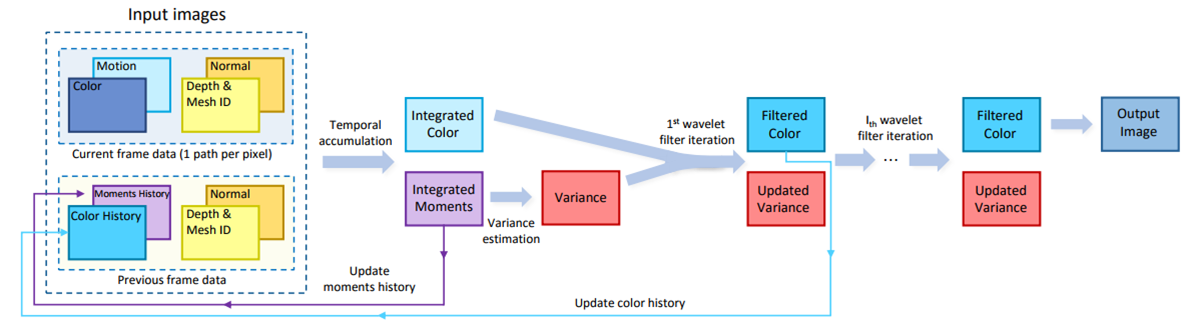
図3
コア再構成フィルタの概要(図2の青色のボックス)
我々は時間的に統合されたカラーとモーメントを得るために、ディープフレームバッファ(左)を時間的にフィルタリングします。推定された輝度分散を使用して、エッジ認識型空間ウェーブレットフィルタ(中央)を駆動します。ウェーブレットフィルタの最初の反復は、将来のフレームを一時的にフィルタリングするのに役立つカラーおよびmoments historyを提供します。 再構成された結果(右)は図2に戻り、アルベドを再変調し、トーンマッピングを実行し、最終的な一時的なアンチエイリアシングパスを実行します。
Post Processing
再構築後、今日のリアルタイムレンダリングの多くに似た後処理を実行します。我々のフィルタリングされた結果は、ハイダイナミックレンジを扱うトーンマッピング処理を通ります。最後に、再構成フィルタが保持する幾何学的エッジに沿った時間的安定性とフィルタエイリアシングを増加させるためのtemporalアンチエイリアシング[Karis 2014]を実行します。
4. SPATIOTEMPORAL FILTER
我々の再構成フィルタは、ラスタ化されたGバッファ(Saito and Takahashi 1990)および以前のフレームの再構成からの履歴バッファとともに、パストレースされた1 sppのカラーバッファを入力として使用します。再構成された画像と、次のフレームのための履歴バッファを出力します。
私たちのGバッファには、主な可視性のためにラスタライズパスから生成された深度、オブジェクト空間およびワールド空間の法線、メッシュID、およびスクリーンスペースの動きベクトルが含まれています。私たちの履歴バッファには、時間的に統合されたカラーとカラーmomentデータと、以前のフレームの深度、法線、およびメッシュIDが含まれています。堅牢性を高めるため、光の位置、形状、その他のシーンのプロパティなど、シーン固有の情報を意図的に使用しないようにしています。特定の光の転送方法は想定していません。
補足
ここでいうモーメントは分散を計算するためのモーメントのことです。
詳細については、こちらをご覧いただくといいと思います。
4.1 Temporal Filtering
ビデオゲームにおけるスーパーサンプリングに広く採用されているtemporal アンチエイリアス(TAA)[Karis 2014]では、これをリアルタイムパストレースに適用するのは当然のように思われます。残念なことに、色に基づく時間フィルタリングは、非常にノイズの多い入力に適用するとアーティファクトを招きます。 Nehabら[2007]およびYang et al [2009]のアイデアからインスパイアされたジオメトリベースの時間フィルタを代わりに採用することで、これらのアーチファクトを最小限に抑え、有効なサンプル数を増やします。
TAAの場合と同様に、フレーム$i$の各色サンプル$C_i$に関連付けられた2D動きベクトルが必要です。
これは、 前のフレームのスクリーン空間位置に$C_i$を逆投影することを可能にします。
カラー履歴バッファにアクセスすることにより、我々のフィルタによって前のフレームで出力し、複数のフレームにわたってカラーサンプルを連続的に蓄積することができます。各$C_i$について、色履歴バッファからサンプル$C_{i-1}$を探し出し、2つのサンプルの深度、オブジェクト空間法線、およびメッシュIDを比較して、それらが一貫している(すなわち、同じ表面上にある)かどうかを判定します。
これらの一貫性テストは、以前の研究でフラグメントマージヒューリスティクスと同様の経験的類似性メトリクスを使用しています[Jouppi and Chang 1999; Kerzner and Salvi 2014]。一貫したサンプルは、指数移動平均を介して新しい統合色$C^{’}_i$として蓄積されます。
C^{'}_i=\alpha\bullet{C_i}+(1-\alpha)\bullet{C^{'}_{i-1}}
ここで、αは時間遅れを制御し、遅れに対する時間的安定性を提供します。私たちは$\alpha=0.2$がベストだと考えています。
私たちの動きベクトルは現在、カメラと剛体の動きを扱いますが、ヒストリバッファに多くのデータを追加し、やや複雑な整合性テストを行うことで、より複雑な変換が可能となります。動きのある画質を改善するために、2×2タップbilinearフィルタを使用して$C_{i-1}$を再サンプリングします。各タップは、逆投影された深度、法線、およびメッシュIDを個別にテストします。
タップに一貫性のないジオメトリが含まれている場合、サンプルは破棄され、そのウエイトは一定したタップにわたって均等に再配分されます。一貫性のあるタップがない場合は、より大きな3×3フィルタを試して、葉のような細い形状を見つけるのを助けます。一貫したジオメトリを見つけられない場合、サンプルはdisocclusion(前のフレームには存在しないピクセル)を表しているので、一時的な履歴を破棄して$C^{'}_{i}=C_i$を使用します。
4.2 Variance Estimation
A-trous ウェーブレットフィルタを信号に局所的に調整するために、ノイズを検出するための効率的なプロキシとして時間積算を用いて色輝度のピクセルごとの分散を推定します。重要なアイデアは、私たちの再構成が、ノイズがほとんどまたは全くない領域(例えば、完全に影になっている領域)でサンプルを変更することを避け、疎にサンプリングされたノイズの多い領域でより多くフィルタリングすることです。
時間の経過とともに異なるサンプルを分析することにより、フィルタは特定のサンプルの信頼性を検出します。空間的に計算された分散推定値は、雑音に対して不完全な代理を与えるだけであることに留意してください。ノイズは分散を増加させますが、分散はノイズなしで発生することができます。
色輝度の1次と2次の生のモーメント$\mu_{1i}$、$\mu_{2i}$を使用して、ピクセルごとの輝度分散を推定します。有意義な推定のために十分に多くのサンプルを収集することで、これらのモーメントを一時的に蓄積し、ジオメトリ一貫性テストを再利用します。積分されたモーメント$\mu_{1i}^{'}$、$\mu_{2i}^{'}$から簡単な公式を使い時間的な分散を見積もります。
{\sigma_{i}^{'}}^{2}=\mu_{1i}^{'}-{\mu_{2i}^{'}}^{2}
カメラのモーション、アニメーション、およびビューポートの境界はすべて、変動予測の品質に影響を与えるdiocclusionイベント(前のフレームには存在しないピクセルの発生)を引き起こします。我々の時間的履歴が制限されている場合(disocclusion後4フレーム未満)、代わりに分散$\sigma$を深度とワールド空間法線によって駆動される重みを備えた7×7のバイラテラルフィルタを使用して、空間的に推定します。
特に、disocclusion(前のフレームには存在しないピクセルの発生)後の数フレームの間は、私たちのフィルタは安定した推定のために十分な時間的な蓄積データが収集されるまでは分散の空間的な見積もりに頼ることになる。
4.3 Edge-avoiding a-trous wavelet transform
Edge-avoiding a-trous wavelet transformについては、こちらで解説しています。
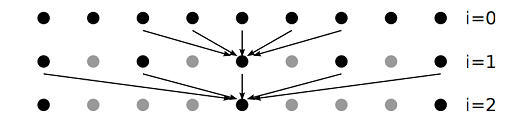
a-trousウェーブレット変換は、各フットプリントが増加するが、非ゼロ要素が一定数である複数の反復にわたって階層的にフィルタリングします(図4参照)。細部係数を破棄すると入力が平滑化されますが、エッジストップ機能は境界でフィルタの範囲を制限することで鮮明な細部を保持します。
図4
1次元ウェーブレット変換の3つのレベルの図。
矢印は、フィルタ内の非ゼロエントリに対応するピクセルを示し、次のレベルの中心ピクセルを計算するために使用されます。灰色のドットは、完全に未確認のウェーブレット変換が考慮する位置ですが、A-Trousアルゴリズムによってスキップされます。
ラスタライズされたGバッファには確率的ノイズが含まれていないため、Gバッファ属性を使用して共通サーフェスを識別するエッジ停止機能を定義できます。我々の実装は、画素$p$、$q$間の重み関数$w(p,q)$を有する5×5のクロスバイラテラルフィルタを用いてエッジ認識型のa-trousウェーブレット分解の各ステップを実現します[Dammertz et al [2010]]。
\hat{c}_{i+1}(p)=\frac{\sum_{q\in{\Omega}}h(q)\bullet{w(p,q)}\bullet{\hat{c}_{i}(q)}}{\sum_{q\in{\Omega}}h(q)\bullet{w(p,q)}}\cdots(1)
$h=(\frac{1}{16},\frac{1}{4},\frac{2}{8},\frac{1}{4},\frac{1}{16})$はフィルタのカーネルです。$\Omega$は収集するフィルタのピクセル範囲です。
重み関数$w(p,q)$は典型的にジオメトリおよび色に基づくエッジストップ関数を組み合わせます[Dammertz et al. 2010]。私たちの新しい重み関数は、代わりに深度、ワールド空間法線、フィルター入力の輝度を使用します。
w_{i}(p,q)=W_{z}\bullet{w_{n}}\bullet{w_{l}}\cdots(2)
ウェーブレットフィルタを適用する前に、輝度分散のローカル推定値に基づいて輝度エッジストップ機能を調整します(4.4節参照)。
次に、式(1)のように時間的に統合された色にウェーブレットフィルタを適用し、分散サンプルが無相関であると仮定することによって、以下のようにフィルタリングします。
Var(\hat{c}_{i+1}(p))=\frac{\sum_{q\in{\Omega}}h(q)^2\bullet{{w(p,q)}^2}\bullet{Var(\hat{c}_{i}(q))}}{(\sum_{q\in{\Omega}}h(q)\bullet{w(p,q)})^2}
この結果を使用して、エッジストッピング関数を次のレベルの変換用に操作します。再構成では、5レベルのウェーブレット変換を使用し、有効な65×65ピクセルのサンプリング範囲を与えます
ウェーブレット変換の一環として、最初のウェーブレットiterationからフィルタリングされたカラーを、将来のフレームと時間的に統合するために使用されたカラー履歴として出力します(図3参照)。我々は、他のウェーブレットレベルからのフィルタリングされた色を使用することができましたが、経験的に最初のWavelet iterationを時間方向への統合に使用することは空間フィルタリングからのバイアスによる時間安定性を改善するベストなバランスであることがわかりました。
4.4 Edge-stopping functions
我々のリアルタイム要件が与えられたとき、時間的安定性とロバスト性を最大化するために、式2の3つのエッジストップ機能を選択しました。サンプルをrejectする各functionの能力は、パラメータ$\sigma_z$、$\sigma_n$および$\sigma_l$によって個別に制御される。これらのパラメータの値の範囲は有効ですが、実験によって、$\sigma_z=1$、$\sigma_n=4$、$\sigma_l=128$がテストしたすべてのシーンでうまく機能することがわかりました。このため、これらのパラメータはユーザーに公開されません。
現実的なシーンには、幾何学的なスケール(geometric scale)に大きな変化が含まれることがよくあります。特にopen lanscalesなシーンで。これにより、グローバルなエッジストップ機能を制御するのが難しくなります。
したがって、surface depthの局所線形モデルを仮定し、クリップ空間平面からの偏差を測定します。我々は、クリップ空間深度のスクリーン空間偏微分を用いて局所深度モデルを推定します。
w_z=exp(-\frac{|z(p)-z(q)|}{\sigma_z{|\nabla{z(p)}\bullet{(p-q)}|}+\epsilon})\cdots(3)
$\nabla{z}$はスクリーンスペースにおけるクリップ空間の深度の勾配です。$\epsilon$はゼロ割り算を回避するための値です。
我々は、ワールド・スペース法線に対するエッジ・ストップ関数の余弦項(cosine term)を採用しています。
w_n=max(0, n(p)\bullet{n(q)})^{\sigma_n})\cdots(4)
$n(p)$はピクセル位置$p$における法線となります。メッシュ単純化とアンチエイリアスアルゴリズムの以前の研究では、2つのサーフェスを結合するかどうかを制御するために似たような計算を使用しています。
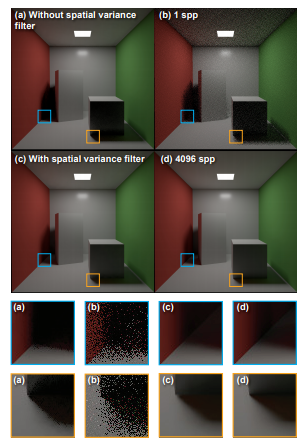
輝度edge stopping functionの重要な側面は、ローカル標準偏差に基づいて輝度を再標準化することによって、すべてのスケールに自動的に適応する能力です。しかし、低いサンプル数で動作させると、分散と標準偏差の推定値が不安定になります。これによりアーティファクトが導入される可能性があります。これを回避するために、3×3ガウスカーネルを使用して分散画像を事前フィルタリングし、再構成品質を大幅に改善します(図5参照)。
図5
輝度edge stopping functionは以下のようになります。
w_l=exp(-\frac{|l_{i}(p)-l_{i}(q)|}{\sigma_l{\sqrt{g_{3x3}(Var(l_{i}(p)))}}+\epsilon})\cdots(5)
$g_{3x3}$は3x3のガウスフィルタ、$l_{i}(p)$はピクセル位置$p$における輝度となります。輝度分散はその後のフィルタiterationで減少する傾向があるので、$w_l$の影響は各iterationで増大し、ぼかしを防止します。このガウスプレフィルタは、輝度edge stopping functionを駆動するためにのみ使用され、ウェーブレット変換の次の反復に伝播される分散画像には適用されないことに留意してください。
補足
どうもこの論文の実装にはFalcorを使っているそうです。
要約
私の理解で手順を簡単にまとめると、以下のようになります。
- G-Buffer作成
- ラスタライザで法線、深度、モーションベクトルをG-Bufferに出力
- Path Tracing
- Halton列を使用
- Path Regularization
- Next Event Estimation
- Shadow Rayは2つ飛ばしている
- Direct Lighting、Indirect Lightingとそれぞれレンダリング
- Temporal Accumulation
- Temporal Reprojectionにより過去のフレームに対してレンダリング結果を蓄積
- 分散計算用のモーメントを更新
- Variance Estimation
- 4フレーム以上蓄積されていないピクセルに対して、7x7タップでVariance Estimationを行う
- 4フレーム以上蓄積されている場合はモーメントから分散を計算
- A-trous Wavelet
- G-Bufferおよび分散からedge stopping functionを使って、A-trous wavelet filterを行う
- 最初のイテレーションのフィルタした結果は次のフレームのtemporal filterを蓄積先のデータとして利用
- Temporal Anti Aliasing
- 最後にTAAを行うことで、1sppレンダリングによるピクセルのブレを抑制
処理は複雑ですが、1つ1つの処理はシンプルだと思われます。ポイントは、以下と思っています。
- リプロジェクションを行うことでプログレッシブレンダリングされるようにすることで、カメラの移動などインタラクションが発生したときでもレンダリングをクリアしないようにしている。
- 分散を利用することでA-trous wavelet filterの品質を上げている。
実装
さすがにコードをここに記載するには大きすぎるので、それはしません。私がどういう実装しているのか、つまづいたところ、工夫したところ、よく理解できていないところをここに書きます。
Path Tracing
Next Event Estimationをしています。Path Regularizationはしていません。とくに特別なことはしていません。Direct LightingとIndirect Lightingを分離していません。私の実装が悪いのか試してみたところ、あまり品質に差がなかったためです。
Temporal filtering
アニメーションには対応していないのでモーションベクトルは使わずに前のフレームのカメラマトリクスを使って、計算しています。3x3の範囲を見てフィルタした結果を蓄積しています。法線、深度、メッシュIDなどを見て中心ピクセルに対して差が大きいものの寄与が下がるようにしています。
Variance Estimation
具体的な計算方法が示されていないので、自分流です・・・。いまいち品質が上がらないのはここが原因ではと思っています。7x7の範囲を法線、深度、位置からウエイトを計算してフィルタリングすることで計算しています。
A-trous wavelet
ここは説明が十分だったので、そんなに迷わなかったです。
ただ、以下の式で、
w_z=exp(-\frac{|z(p)-z(q)|}{\sigma_z{|\nabla{z(p)}\bullet{(p-q)}|}+\epsilon})\cdots(3)
$\nabla{z(p)}$て具体的にどういう計算なのかわからなかったので、著者に確認したところ、ddx、ddyを使っているだけだよ、とのことでした。
Temporal Anti Aliasing
High-Quality Temporal SupersamplingとTemporal Reprojection Anti-Aliasing in INSIDEを参考にしています。
特にTemporal Reprojection Anti-Aliasing in INSIDEはgithubにソースコードもアップされています。(ただし、Unityのコードです)
が、ここも私の実装がダメダメなせいか、いまいち品質がよくありません・・・。
誰か、これ参考するといいよ、という単体動作するソースコード教えてください・・・。
結果
みんな大好きSponza(布無し)を512x512の解像度でレンダリングしたものです。
これで1sppのレンダリングですので、悪くないのではないでしょうか。
各ステップの比較は以下となります。
TAAしてない結果だとfire flyが出てしまいました。High-Quality Temporal Supersamplingを参考にして、TAA内部で抑制するような処理をしています。
肝心のカメラを動かしたときですが、以下です。
粒のようなノイズが発生しているのがわかります。これが、私がVariance Estimationがうまくいってないのではないか、と言った理由です。
ちなみに、カメラが動いているときのVariance Estimationの様子が以下です。
動いている様子を見せているわけではないので、わかりにくいですが、
変化の大きいところは白くなっていて、変化の小さいところは黒くなっています。
性能
論文では、1920x1080で10msだ、みたいなことを書いていますが、私の実装ではそんなに性能がでていません。単純なパストレだけでもそんなに性能が出ません。どういう実装をしたらそこまで速くなるのでしょうか・・・。
GTX1080上でCUDAを使って実装していますが処理時間はパストレーシングとフィルタリングを合わせて、解像度512x512、5bouceで約31ms。解像度1280x720、5bounceですと、約103msとなります。
TAA以外のフィルタ処理をCUDAで実装しているのですが、こちらも論文で書かれている性能が出ていません・・・。どうも論文はフィルタ処理はGLSLで実装しているようです。
制約事項
Introductionにも書かれていますが、被写界深度、モーションブラーはサポートされません。ポストエフェクト処理でリアルタイムグラフィックス手法で実現する必要があります。
あとは、反射がボケたり、シャープな影がボケるそうです。さらに、過去フレームの情報を利用するためカメラを動かしたりすると輝度差が激しい個所では残像が発生するそうです。
また、鏡、半透明といったマテリアルのピクセルのフィルタリングがぼけてしまうと思われます。ただ、これについては鏡に写っているピクセルは2回目のバウンスしたものなので、2回目のバウンスの法線、深度などの情報を利用することで回避できると思われます。(Pixarでもデノイズ用に2回目以降のバウンスの法線などの情報を保持しているようです)
最後に
是非これをきっかけに誰か実装してみてください。
論文と同じ性能、品質が出たぜ、という人はぜひ私に教えてください・・・。