Go to Qiita Advent Calendar 2024 Top
LoginSignup
15
13

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

GraphicsAdvent Calendar 2017Day 4
@nackdai

レイトレーシングレンダリングのデノイズを考える（その１）Edge-Avoiding A-Trous Wavelet Transform for fast Global Illumination Filtering

Last updated at Posted at 2017-10-01

最初に

この記事に興味を持った人はすでにレイトレーシングとノイズについては知識を持っていると思いますので、レイトレーシングとノイズについての説明は割愛させていただきます。

どのような内容か

ざっくり言うと、G-Buffer（位置、色、法線）を使って、エッジがボケないフィルタリングを行うことでデノイズを行う手法となります。
近年はやりの傾向がある統計解析的な手法やそこから発展した機械学習の手法ではなく、あくまでも画像処理的な手法となり、シンプルな方法だと思われます。

なぜこれを選んだのか

疑似コードが紹介されていて、実装が簡単にできそうだったからです。
あと、この次に投稿しようとおもっているネタがこの論文をベースにしていたからです。

雑訳

雑訳とはいえ、全部を載せるのは大変なので、Edge-Avoiding A-Trous Wavelet Transform for fast Global Illumination FilteringのIntroductionとコア部分である２章のみの超雑訳となります。
超雑訳ですので、細かいところで意味がわからない（そもそも私も理解できていない）ところもあると思いますが、ご容赦ください。

Introduction

モンテカルロベースのグローバルイルミネーションレイトレーシングは、最も柔軟で堅牢なライトトランスポートシミュレーションアルゴリズムの1つです。
多くの異なるアプローチが存在するが、それらはすべてレンダリング方程式の積分を解くためにランダムパスサンプリングを使用します。

通常、滑らかな画像を得るためには、ピクセルあたり数百のパスが必要です。しかし、現代のコンピュータやアルゴリズムでさえ、インタラクティブなアプリケーションや高速プレビューに必要な時間枠内でピクセルあたりわずかなパスしか提供できません。
ランダムパス数を制限することは目立つノイズを含む画像を生成することになります。そのため、高速でfast undecimated A-Trous wavelet transformを拡張して、複数のエッジ停止機能を組み込み、ノイズの多いモンテカルログローバルイルミネーション画像を確実に（robustly）フィルタリングし、インタラクティブなレートで視覚的に満足できる結果を引き出すことができることを示します。

追加のラスタライズされた画像からの情報でCPUベースのレイトレーサの出力を補完するハイブリッド技術を使用します。私たちのGPUシェーダは、異なるバッファを組み合わせたEdge-AvoidingA-Trousフィルタを適用して、出力イメージを生成します。

この論文の主なポイントは以下のとおりとなります。

  • the interactive edge-avoiding A-Trous filter

  • an edge-stopping function (depending on edges in geometry and illumination) for noisy path traced images

  • comparison to other (edge and non edge-avoiding) wavelet bases for reconstruction of Monte Carlo images.

これにより、高精細（例えば、シャープな影）を保持するインタラクティブなレートで視覚的に滑らかな外観のパストレースされたグローバルイルミネーション画像を生成することができます。

2. Edge-Avoiding A-Trous Filtered Path Tracing

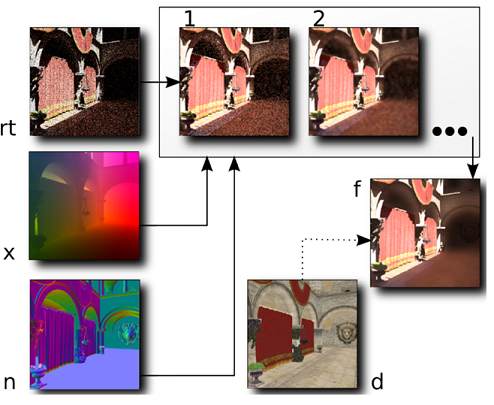
atrous_fig2.png

図2：オーバービュー
rt)、n)、x)は入力バッファです。（それぞれ、RayTracing（レイトレーシング）、Normal（法線）、WorldSpacePosition（ワールド空間座標））。1)、2)は私たちのedge-avoiding A-Trous フィルタの２レベルの処理結果を表しています。f)はトーンマッピング後の最終出力結果です。d)はオプションのディフューズバッファです。

図2は、私たちのアルゴリズムの基本ステップを示しています。
入力はpath traced image(noisy)（rt buffer）で、最も単純な場合には直接照明と間接照明の両方が含まれます。
さらに、A-Trousフィルタのエッジストップ機能は、法線バッファとpositionバッファを考慮しています。
A-Trousフィルタの適用数は、所望の全フィルタサイズ（今回は、5 iterations, i.e. 80×80）によって決定されます。
エッジがない場合（例えば、すべてのバッファが単色）、iterationごとにフィルタサイズを増加させて平滑化を適用します。
エッジが存在する場合、隣接するサンプルの影響は、エッジ停止機能によって低減されます。
これはバイラテラルフィルタと密接に関連し、[FAR07]のA-Trousアルゴリズムと[Fat09]のデシメーション（ダウンサイジング）ウェーブレットベースで使用されました。

2.1. Monte Carlo Light Transport

モンテカルロ法は、カメラをシーン内の光源に接続するランダムパスを構築することによって、レンダリング方程式[Kaj86]の積分を解きます。
これは完全レンダリングの式の最も一般的な既知の解であり、文献でよく研究されています。
モンテカルロイメージの1つの問題 合成は、単純なシーンでも見える高い分散です。
この分散を2次的に減少させるために、線形改善のためにより多くのサンプルが必要とされます。
我々のシステムでは、基本的な画像形成アルゴリズムとして、next event estimationを使用する。
このパストレーサは、カメラからの光をランダムウォークとしてシーンにトレースすることから始まります。
各ヒットポイントにおいて、光源上のランダムに選択された位置への接続が行われます。
遮蔽されていない場合、この経路の寄与が画像蓄積バッファに加えられます
次のセクションでは、最終的なray traced imageの分散を減少させる平滑化プロセスについて説明します。
これは、以下の観察によって動機づけられます。
表面上の単一点における入射放射照度は、 半球上で積分します。
インタラクティブまたはリアルタイムの制約の下では、パス・トレーサは1pixelにつき1pathしかトレースすることができず、従って、単一のサンプルのみで積分を推定します。
しかし、隣接する半球が類似していれば、同様の積分を期待します。したがって、平滑化は、同様の半球でサンプルを平均化しようとします。

2.2. Edge-Avoiding A-Trous Filter

このセクションでは、（重み付けされていない）A-Trousウェーブレット変換について説明し、その後、エッジ・ストップ関数を組み込むように拡張します
A-Trousアルゴリズムの各反復（ステップ幅が増加する）は、ウェーブレット解析のもう1つのレベルを計算することに対応します。これは、フィルタサイズを2倍にすることにも相当します。
[Bur81]は、広いガウスフィルタは、カーネルを生成することと繰り返し畳み込むことでよく近似できることを示しています。
[HKMMT89]は、この構造を使用して離散ウェーブレット変換を計算します。これはアルゴリズムA-Trousとして知られています。

  1. At level $i=0$, we start with the input signal $C_0(p)$.
  2. $C_{i+1}(p)=C_i(p) * h_i$, $*$ は離散畳み込みである。フィルタ$h_i$内のエントリ間の距離は$2^i$である。
  3. $d_i(p)=C_{i+1}(p)-C_i(p)$ ここで$d_i(p)$はレベル$i$のディテールまたはウェーブレット係数です。
  4. if $i < N$ (number of levels to compute) increment $i$, go to step 2
  5. $\{d_0, d_1,...,d_{N-1}, C_N\}$ は$c$のウェーブレット係数である。

再構成は、以下の式によって与えられます。

c=c_N+\sum_{i=N-1}^{0}d_i

フィルター$h$はB3スプライン補間をベースにしています。

\{\frac{1}{16},\frac{1}{4},\frac{3}{8},\frac{1}{4},\frac{1}{16}\}

各レベル$i>0$において、フィルタは最初のエントリの間に$2^{i-1}$個のゼロを埋め込むことによって、その範囲を２倍にします。
したがって、非ゼロエントリーの数は一定のままとなります。(図3)

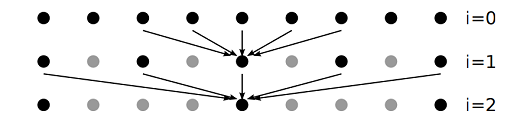
atrous_fig3.png

図3 : A-Trousウェーブレット変換の3つのレベル。
矢印は、フィルタ$h_i$内の非ゼロエントリに対応するピクセルを示し、次のレベルの中心ピクセルを計算するために使用されます。灰色のドットは、完全に未確認のウェーブレット変換が考慮する位置ですが、A-Trousアルゴリズムによってスキップされます。

エッジ回避フィルタリングは、データ依存重み付け関数を導入することによって達成されます。
我々は、バイラテラルフィルタの強度ベースのエッジ停止関数を拡張し、複数のエッジ停止関数を組み合わせます。
ステップ2の離散畳み込みは次のようになります。

c_{i+1}(p)=\frac{1}{k}\sum_{q\in\Omega}h_i(q)w(p,q)c_i(q)

$w$は重み関数、$p,q$はピクセル位置、$\Omega$は$h_i$の中の非ゼロ係数の位置の集合です。

$k$は正規化項で、 $k=\sum_{q\in\Omega}h_i(q)w(p,q)$となります。

$w$はレイトレースイメージ(rt)、法線(n)、位置(x)バッファからのエッジ停止関数を組み合わせたものです。

w(p,q)=w_{rt}w_nw_x

w_{rt}=e^{(\frac{|I_p-I_q|}{\sigma})}

$I_p, I_q$は位置$p, q$におけるrt(ray trace)バッファのカラー値です。
$w_n, w_x$も同様の方法で計算することができます。

このフィルタはGLSLで実装されており（ソースコードの最後を参照）、ステップ幅（つまり、 フィルタエントリ間のゼロの数）、フィルタ$h$、パラメータ$\sigma_{rt}, \sigma_n, \sigma_x$をユニフォーム変数、画像rt、n、xをテクスチャとして指定します。

レイトレース画像に含まれるノイズについては仮定を立てることが難しいため、レイトレース画像の最大強度のスケールの変動を含めるように初期の$\sigma_{rt}$を選択します。HDR環境では強度が1よりも大きくなる可能性があることに注意してください。したがって、エッジ停止機能は、$w_n$および$w_x$上の第1レベルにのみ依存します。各パスで、${\sigma_{rt}}^i$を$2^{-i}\sigma_{rt}$に設定して、より小さな照明変化を平滑化することができます。

私たちのエッジストップ機能によって保存されているエッジは、より粗いレベルのトランスフォーメーションではまだ存在しています。 したがって、我々はウェーブレット変換のより細かいレベルを破棄し、A-Trousアルゴリズムのステップ3を不要にし、出力画像としてレベルNを直接使用します。

実装解説

で、実際に実装してみたので、どう実装したのかを説明します。

以下は、論文内に記載されている疑似コードとなります。

疑似コード
uniform sampler2D colorMap, normalMap, posMap;
uniform float c_phi, n_phi, p_phi, stepwidth;
uniform float kernel[25];
uniform vec2 offset[25];

void main(void) {
    vec4 sum = vec4(0.0);
    vec2 step = vec2(1./512., 1./512.); // resolution

    vec4 cval = texture2D(colorMap, gl_TexCoord[0].st);
    vec4 nval = texture2D(normalMap, gl_TexCoord[0].st);
    vec4 pval = texture2D(posMap, gl_TexCoord[0].st);

    float cum_w = 0.0;

    for(int i = 0; i < 25; i++) {
        vec2 uv = gl_TexCoord[0].st + offset[i]*step*stepwidth;

        vec4 ctmp = texture2D(colorMap, uv);
        vec4 t = cval - ctmp;
        float dist2 = dot(t,t);
        float c_w = min(exp(-(dist2)/c_phi), 1.0);

        vec4 ntmp = texture2D(normalMap, uv);
        t = nval - ntmp;
        dist2 = max(dot(t,t)/(stepwidth*stepwidth),0.0);
        float n_w = min(exp(-(dist2)/n_phi), 1.0);

        vec4 ptmp = texture2D(posMap, uv);
        t = pval - ptmp;
        dist2 = dot(t,t);
        float p_w = min(exp(-(dist2)/p_phi),1.0);

        float weight = c_w * n_w * p_w;
        sum += ctmp * weight * kernel[i];
        cum_w += weight*kernel[i];
    }

    gl_FragData[0] = sum/cum_w;
}

だいぶシンプルな実装なので、解説はほとんどいらないと思います。

私のかなり怪しい理解では、画像のウェーブレット変換はフィルタを掛けながら、画像を縮小し、縮小された画像ほど高周波が残るので、同じように画像を縮小しながらノイズフィルタを掛け、残った高周波ノイズを消していくということなのかと思っています。ただし、画像を縮小するのではなく、参照するピクセル位置のステップサイズを大きくすることで同様の効果を得ています。

以下が、私の実装したGLSLコードです。

実装
uniform sampler2D s0;    // rt buffer.
uniform sampler2D s1;    // normal map.
uniform sampler2D s2;    // position map.

// NOTE
// pow(2, iteration)
uniform int stepScale;

// NOTE
// pow(2, -iteration)
uniform float clrSigmaScale = 1.0;

uniform float clrSigma = 0.125;
uniform float nmlSigma = 0.125;
uniform float posSigma = 0.125;

layout(location = 0) out vec4 oOut;

// NOTE
// h = [1/16, 1/4, 3/8, 1/4, 1/16]
// H = h * h
const float kernel[25] = float[25](
    1.0 / 256.0, 1.0 / 64.0, 3.0 / 128.0, 1.0 / 64.0, 1.0 / 256.0,
    1.0 / 64.0, 1.0 / 16.0, 3.0 / 32.0, 1.0 / 16.0, 1.0 / 64.0,
    3.0 / 128.0, 3.0 / 32.0, 9.0 / 64.0, 3.0 / 32.0, 3.0 / 128.0,
    1.0 / 64.0, 1.0 / 16.0, 3.0 / 32.0, 1.0 / 16.0, 1.0 / 64.0,
    1.0 / 256.0, 1.0 / 64.0, 3.0 / 128.0, 1.0 / 64.0, 1.0 / 256.0);

// NOTE
// 5x5
const ivec2 offsets[25] = ivec2[25](
    ivec2(-2, -2), ivec2(-1, -2), ivec2(0, -2), ivec2(1, -2), ivec2(2, -2),
    ivec2(-2, -1), ivec2(-1, -1), ivec2(0, -2), ivec2(1, -1), ivec2(2, -1),
    ivec2(-2, 0), ivec2(-1, 0), ivec2(0, 0), ivec2(1, 0), ivec2(2, 0),
    ivec2(-2, 1), ivec2(-1, 1), ivec2(0, 1), ivec2(1, 1), ivec2(2, 1),
    ivec2(-2, 2), ivec2(-1, 2), ivec2(0, 2), ivec2(1, 2), ivec2(2, 2));

void main()
{
    vec4 sum = vec4(0.0);
    float weightSum = 0.0;

    ivec2 centerUV = ivec2(gl_FragCoord.xy);

    vec4 centerClr = texelFetch(s0, ivec2(gl_FragCoord.xy), 0);
    vec4 centerNml = texelFetch(s1, ivec2(gl_FragCoord.xy), 0);
    vec4 centerPos = texelFetch(s2, ivec2(gl_FragCoord.xy), 0);

    int centerMtrlId = int(centerPos.w);
    int centerMeshId = int(centerNml.w);

    if (centerMeshId < 0) {
        // This is background.
        oOut= vec4(1, 1, 1, 1);
        return;
    }

    centerPos.w = 1.0f;
    centerNml.w = 0.0f;

    // NOTE
    // 5x5 = 25
    for (int i = 0; i < 25; i++) {
        ivec2 uv = centerUV + offsets[i] * stepScale;

        vec4 clr = texelFetch(s0, uv, 0);
        vec4 nml = texelFetch(s1, uv, 0);

        vec4 pos = texelFetch(s2, uv, 0);

        int mtrlId = int(pos.w);
        int meshId = int(nml.w);

        if (meshId < 0) {
            // Ignore background.
            continue;
        }

        nml.w = 0.0f;
        pos.w = 1.0f;

        if (mtrlId != centerMtrlId || meshId != centerMeshId) {
            // Ignore different material or mesh.
            continue;
        }

        vec4 delta = clr - centerClr;
        float dist2 = dot(delta, delta);
        float w_rt = min(exp(-dist2 / (clrSigma * clrSigmaScale)), 1.0);

        delta = nml - centerNml;
        dist2 = dot(delta, delta);
        float w_n = min(exp(-dist2 / nmlSigma), 1.0);

        delta = pos - centerPos;
        dist2 = dot(delta, delta);
        float w_p = min(exp(-dist2 / posSigma), 1.0);

        float weight = w_rt * w_n * w_p;

        sum += clr * weight * kernel[i];
        weightSum += weight * kernel[i];
    }

    oOut = sum / weightSum;
}

疑似コードでは、法線の差分の内積をイテレーションごとのステップサイズの２乗で除算しています。たぶんこれはイテレーションごとに法線の影響を小さくしたいのではと思っているのですが、試したところ品質が下がってしまいましたのでやっていません。
また、私はG-BufferにメッシュID、マテリアルIDを含めて、異なるメッシュの値は拾わないようにしています。ちなみにunifromの初期値は適当です。

そして、呼び出し側の処理（一部）が以下となります。

呼び出し側の処理
glUseProgram(program)

for (int i = 0; i < 5; i++) {
    // Bind textures
    if (i == 0) {
        // Bind original image.
    }
    else {
        // Bind previous iteration FBO as texture.
    }

    // For A-trous wavelet.
    int stepScale = 1 << i;

    float clrSigmaScale = powf(2.0f, i);

    auto handle = glGetUniformLocation(program, "stepScale");
    glUniform1i(handle, stepScale);

    handle = glGetUniformLocation(program, "clrSigmaScale");
    glUniform1f(handle, clrSigmaScale);

    // Other uniforms
    ....

    // Bind FBO as render target.
    ...

    // Draw
    ....
}

各イテレーションごとに計算が必要な値をシェーダに渡して、描画しています。ここで気を付けることは、FBOに書き出して、それを次のイテレーションの入力として使うことです。

結果

パラメータは適当に設定しているため、バンドみたいなものが出てしまっていますが
8sppでここまでノイズが消えれば、まずまずではないでしょうか。

atrous_result.png

処理時間は測定していませんが、5イテレーション回しているので、それなりの処理時間だと思われます。
それでもNonLocalMeanフィルタよりはだいぶ軽いのではないでしょうか。

制約事項

論文では、以下の２点を制約事項として書かれています。

  • 複雑な形状のシーンだと法線、深度が隣接ピクセルごとに値が異なりすぎて、十分にフィルタリングできなくなります。
  • フィルタリングするため、Unbiasedでなくなります。

以下は、私が実装してみて、たぶん制約だろうと思うことです。

  • エッジを明確にするため、ピクセルに含まれる情報が１ジオメトリ（１マテリアル）である必要があるため、ピクセル上に複数のジオメトリ（マテリアル）が含まれるぼけたピクセルをフィルタリングに利用できないと思われます。つまり、レンズシミュレーションによる被写界深度、モーションブラーができないと思われます。
  • 鏡、半透明といったマテリアルのピクセルのフィルタリングがぼけてしまいます。ただ、これについては鏡に写っているピクセルは２回目のバウンスしたものなので、２回目のバウンスの法線、深度などの情報を利用することで回避できると思われます。（Pixarでもデノイズ用に2回目以降のバウンスの法線などの情報を保持しているようです）
15
13
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
15
13

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?