ストラング先生の４つの部分空間 ー 四大陸をメタファとして

１ はじめに

ストラング先生の４つの部分空間 ¹⁾ をご存知だろうか？
行列 $A$ の背後にある構造を示す行空間 $C(A^T)$ 、零空間 $N(A)$ 、列空間 $C(A)$ 、そして左零空間 $N(A^T)$ の４つの部分空間のことである（下図）。

私は体調を崩して入院していた。病棟の早い消灯時間が過ぎても眠れない夜、私の頭の中はストラング先生の４つの部分空間によって占められていた。先ほど読んだ同門の @osawat さんの Qiita の記事 ²⁾ のことを考えていたからだ。ずっと眺めていると４つの部分空間が世界地図に見えてきたではないか（下図）。そこで考えた。ストラング先生の４つの部分空間を４大陸になぞらえて解説記事を書いてみてはどうかと。

Weblio辞書を引けば、四大陸とは「アメリカ、アフリカ、アジア、オセアニアのこと」とある。が、ここでは、アジア大陸を行空間 $C(A^T)$、アフリカ大陸を零空間 $N(A)$、北アメリカ大陸を列空間 $C(A)$、そして南アメリカ大陸を左零空間 $N(A^T)$ にたとえる物語を書いてみる。

コラム：ストラング教の住人
伝道師：@kenjihiranabe さん。ストラング先生の代弁者にしてストラング教の住人のリーダー。ストラング教の門徒の尊敬を一身に集める。ストラング先生の経典を翻訳
門徒A：@osawat さん。古くからのストラング教の門徒でストラング教の分派である射影派の熱心な教徒。
門徒B：@kau さん。高齢者が多いストラング教門徒にあって若手の代表格。ストラング教の門徒は理系族が多くを占めるが、珍しい文系族出身。伝道師 @kenjihiranabe さんの崇拝者。新参者の私が密かにライバル視する若手のホープで、かつて私との間に「入力空間－行空間」問題で論争が起こった
門徒C：私。ストラング教の新参者。かつては線形代数を単なる計算の手段としか考えていなかったがストラング教の奥深さに感化され今では回心している。
異端者D：@innovation1005 さん。ストラング教の経典の勉強会 ³⁾ の主催者。一見、門徒のために熱心に布教活動をしているようにも見えるが、実はストラング教の真理を究めるため門徒との議論を通じて自らの啓発を企てる異端（統計準２級教）の教徒

2. 行列 A の構造

$A$ は $m\times n$ の実数を要素に持つ行列である。これを、$A\in \mathbb{R}^{m\times n}$ と書く。
$A$ は $n$ 次元ベクトル $\boldsymbol{v} \in \mathbb{R}^n$ を入力とし、$m$ 次元ベクトル $\boldsymbol{w} \in \mathbb{R}^m (= A\boldsymbol{v})$ を出力する線形変換を表す行列である。入力ベクトル $\boldsymbol{v}$ が存在する空間を $A$ の入力空間 ($V$) 、出力ベクトル $\boldsymbol{w} = A\boldsymbol{v}$ が存在する空間を出力空間 ($W$) と呼ぶことにする。

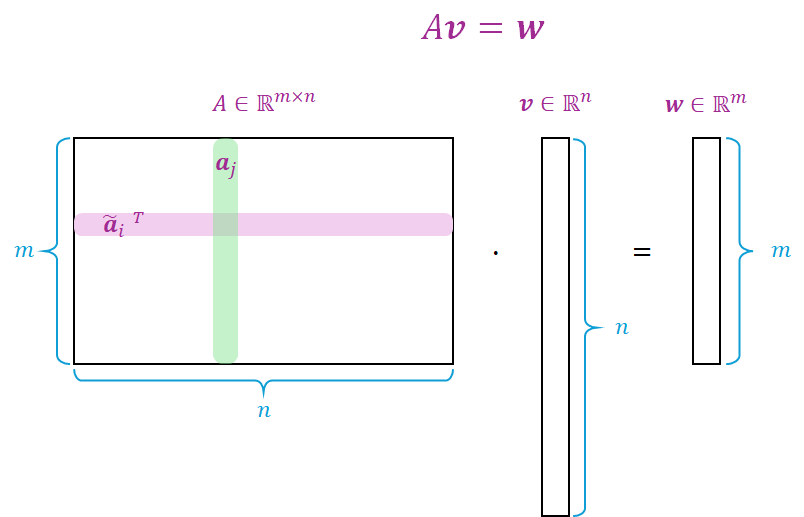
行列 $A$ の $i$ 番目の行ベクトルを $\boldsymbol{\tilde{a}}_i$ 、 $j$ 番目の列ベクトルを $\boldsymbol{a}_j$ とすると、

A =
\begin{bmatrix} {\boldsymbol{\tilde{a}}_1}^T \\ \vdots \\ {\boldsymbol{\tilde{a}}_m}^T
\end{bmatrix}
=
\begin{bmatrix} \boldsymbol{a}_1 & \cdots & \boldsymbol{a}_n \end{bmatrix}

\tag{2.0.1}

のように行ベクトルあるいは列ベクトルを用いて行列を表現することができる。

2.1 行空間

$A$ の行ベクトルから構成される空間、すなわち$A$ の行ベクトルで張られる空間を$A$ の行空間といい、$C(A^T)$ で表す（Fig.3参照）。Fig.1の４つの部分空間の図では左上にある矩形領域が、また、Fig.2の世界地図ではアジア大陸がこれに対応する。
行空間上の任意のベクトルを $\boldsymbol{x}_R \in \mathbb{R}^n$ とすると

\boldsymbol{x}_R = A^T \boldsymbol{y} 
= y_1 \tilde{\boldsymbol{a}}_1 + \cdots + y_m \tilde{\boldsymbol{a}}_m 
\tag{2.1.1}

と表すことができる。ここで、$\boldsymbol{y} = (y_1, \dots, y_m) \in \mathbb{R}^m$ は $A$ の行ベクトルの線形結合の係数を要素とするベクトルである。したがって

C(A^T) = \lbrace \boldsymbol{x} \in \mathbb{R}^n| \boldsymbol{x} = A^T \boldsymbol{y}, \forall \boldsymbol{y} \in \mathbb{R}^m\rbrace \tag{2.1.2}

である。
さて、$C(A^T)$ が $\mathbb{R}^n$ の $n$ 次元空間のうち何次元の部分空間を占めるかは、行列 $A$ の $m$ 個の行ベクトルのうち線形独立な最大個数（これを行列 $A$ のランクという）に依存する。いま、その数を $r$ 個とすると（ただし $r \le \min(n,m)$）、$\boldsymbol{x}_R$ が占める部分空間、すなわち行空間 $C(A^T)$ の次元は $r$ となる。

コラム：行列のランク
行列 $A$ のランクとは、$A$ の列ベクトルもしくは行ベクトルの線形独立な最大個数である。

2.2 零空間

行空間 $C(A^T)$ は入力空間 $V(=\mathbb{R}^n)$ の部分空間で、その次元は $r$ 次元であることは既に述べた。では、入力空間 $V(=\mathbb{R}^n)$ のうち、行空間を除いた残りの部分空間は一体何だろう？
それを考えるには $A$ のすべての行ベクトルと直交するようなベクトルを考えればよい。そのようなベクトルを $\boldsymbol{x}_N \in \mathbb{R}^n$ とすると、

A \boldsymbol{x}_N = 0 \tag{2.2.1}

となる。なぜなら、$A \boldsymbol{x}_N$ は $A$ の各行ベクトルとベクトル $\boldsymbol{x}_N$ の内積を計算したものを並べたベクトルであるが（Fig.3右上参照）、それが $0$ であるということは、$\boldsymbol{x}_N$ は $A$ のすべての行ベクトルと直交することを表しているからである。このような $\boldsymbol{x}_N$ の集合からなる部分空間を行列 $A$ の零空間と呼び $N(A)$ で表す。すなわち、

N(A) = \lbrace \boldsymbol{x} \in \mathbb{R}^n | A \boldsymbol{x} = 0 \rbrace \tag{2.2.2}

である。零空間上の任意のベクトルは行空間上の任意のベクトルと直交するので、零空間は行空間の直交補空間になっている。そして、零空間の次元は $\mathbb{R}^n$ 全体の次元 $n$ から行空間の次元 $r$ を引いた $n-r$ になっている。Fig.1の４つの部分空間の図では左下にある矩形領域が、また、Fig.2の世界地図ではアフリカ大陸が零空間に対応する。

コラム：直交補空間
直交補空間は、ある部分空間の全てのベクトルと直交するベクトル全体の集合のことである。

2.3 入力空間

入力空間上の任意のベクトル $\boldsymbol{x} \in V$ は、行空間上のベクトル $\boldsymbol{x}_R \in C(A^T)$ と零空間上のベクトル $\boldsymbol{x}_N \in N(A)$ の和に分解でき

\boldsymbol{x} = \boldsymbol{x}_R + \boldsymbol{x}_N \tag{2.3.1}

と表すことができる（Fig.1）。つまり、入力空間 $V$ は行空間 $C(A^T)$ と零空間 $N(A)$ の直和空間

V = C(A^T) \oplus N(A) \tag{2.3.2}

である。

2.4 列空間

$A$ の列ベクトルから構成される空間、すなわち$A$ の列ベクトルで張られる空間を$A$ の列空間といい、$C(A)$ で表す（Fig.4参照）。Fig.1の４つの部分空間の図では右上にある矩形領域が、また、Fig.2の世界地図では北アメリカ大陸がこれに対応する。
列空間上の任意のベクトルを $\boldsymbol{y}_C \in \mathbb{R}^m$ とすると

\boldsymbol{y}_C = A \boldsymbol{x} 
= x_1 \boldsymbol{a}_1 + \cdots + x_n \boldsymbol{a}_n \tag{2.4.1}

と表すことができる。ここで、$\boldsymbol{x} = (x_1, \dots, x_n) \in \mathbb{R}^n$ は $A$ の列ベクトルの線形結合の係数を要素とするベクトルである。したがって

C(A) = \lbrace \boldsymbol{y} \in \mathbb{R}^m | \boldsymbol{y} = A \boldsymbol{x}, \forall \boldsymbol{x} \in \mathbb{R}^n \rbrace \tag{2.4.2}

である。
さて、$C(A)$ が $\mathbb{R}^m$ の $m$ 次元空間のうち何次元の部分空間を占めるかは、行列 $A$ の $n$ 個の列ベクトルのうち線形独立な最大個数に依存するが、その数は行列 $A$ のランク $r$ である。よって $\boldsymbol{y}_C$ が占める部分空間、すなわち列空間 $C(A)$ の次元は行空間 $C(A^T)$ の次元と同じく $r$ となる。

2.5 左零空間

列空間 $C(A)$ は出力空間 $W(=\mathbb{R}^m)$ の部分空間であり、その次元は $r$ 次元であった。では、出力空間 $W(=\mathbb{R}^m)$ のうち、列空間を除いた残りの部分空間は一体何だろう？
それを考えるには $A$ のすべての列ベクトルと直交するようなベクトルを考えればよい。そのようなベクトルを $\boldsymbol{y}_N \in \mathbb{R}^m$ とすると、

A^T \boldsymbol{y}_N = 0 \tag{2.5.1}

となる。なぜなら、$A^T \boldsymbol{y}_N$ は $A$ の各列ベクトルとベクトル $\boldsymbol{y}_N$ の内積を計算したものを並べたベクトルであるが（Fig.4右上参照）、それが $0$ であるということは、$\boldsymbol{y}_N$ は $A$ のすべての列ベクトルと直交することを意味しているからである。このような $\boldsymbol{y}_N$ の集合からなる部分空間を行列 $A$ の左零空間と呼び $N(A^T)$ で表す。すなわち、

N(A^T) = \lbrace \boldsymbol{y} \in \mathbb{R}^m | A^T \boldsymbol{y} = 0 \rbrace \tag{2.5.2}

である。左零空間上の任意のベクトルは列空間上の任意のベクトルと直交するので、左零空間は列空間の直交補空間になっている。そして、左零空間の次元は $\mathbb{R}^m$ 全体の次元 $m$ から列空間の次元 $r$ を引いた $m-r$ になっている。Fig.1の４つの部分空間の図では右下にある矩形領域が、また、Fig.2の世界地図では南アメリカ大陸が左零空間に対応する。

2.6 出力空間

出力空間上の任意のベクトル $\boldsymbol{y} \in W$ は、列空間上のベクトル $\boldsymbol{y}_C \in C(A)$ と左零空間上のベクトル $\boldsymbol{y}_N \in N(A^T)$ の和に分解でき

\boldsymbol{y} = \boldsymbol{y}_C + \boldsymbol{y}_N \tag{2.6.1}

と表すことができる（Fig.1）。つまり、出力空間 $W$ は列空間 $C(A)$ と左零空間 $N(A^T)$ の直和空間

W = C(A) \oplus N(A^T) \tag{2.6.2}

である。

3. 連立方程式の解法

3.1 連立方程式

行列の応用として最初に思い浮かぶのは次のような連立方程式の解法だろう。

A \boldsymbol{x} = \boldsymbol{b} \tag{3.1.1}

ここで、$\boldsymbol{x} \in \mathbb{R}^n$ は入力空間 $V$ 上のベクトルで、$\boldsymbol{b} \in \mathbb{R}^m$ は出力空間 $W$ 上のベクトルである。$A \in \mathbb{R}^{m \times n}$ であるから、(3.1.1)式は $m$ 個の連立 $n$ 元方程式を表している。

3.2 右辺の b が列空間上にある場合

まず、最初に言えることは、$\boldsymbol{b}$ が列空間 $C(A)$ 上にない場合、連立方程式 (3.1.1) には解がない。つまり、不能である。なぜなら、左辺の $A \boldsymbol{x}$ は(2.4.1)式で示すように $A$ の列ベクトルの線形結合、すなわち列空間上にあるので、列空間にない右辺の $\boldsymbol{b}$ に一致するがずがない。そこで、この節では $\boldsymbol{b}$ が列空間 $C(A)$ 上にある場合について考える。

2.3節でみたように、入力空間 $V$ 上の任意のベクトル $\boldsymbol{x} \in \mathbb{R}^n$ は、(2.3.1)式のように行空間上のベクトル $\boldsymbol{x}_R \in C(A^T)$ と零空間上のベクトル $\boldsymbol{x}_N \in N(A)$ の和に分解できるので、(3.1.1)式は

A \boldsymbol{x} = A (\boldsymbol{x}_R + \boldsymbol{x}_N) = A \boldsymbol{x}_R + A \boldsymbol{x}_N = \boldsymbol{b} \tag{3.2.1}

と表される。一方、(2.2.1)式より $A \boldsymbol{x}_N = \boldsymbol{0}$ なので、上式は

A \boldsymbol{x} = A \boldsymbol{x}_R = \boldsymbol{b} \tag{3.2.2}

となる。これは何を意味しているかというと、(3.1.1)式の解は一意に決まるのではなく、零空間上のベクトル $\boldsymbol{x}_N$ の分だけ不定性があるということである。@osawat さんは彼のブログ「ストラング先生の4つの部分空間 （行空間と零空間）」³⁾ の中でこの $\boldsymbol{x}_N$ のことを「報われないベクトル」と呼んでいる。言い得て妙である。また、@kenjihiranabe さんのブログ「$A\boldsymbol{x}=\boldsymbol{b}$ を4つの部分空間を使って理解する?連立一次方程式の解の秘密?」⁴⁾ にはこのあたりの話が大変詳しく書いてある。

コラム：A が可逆な場合
$\boldsymbol{b}$ が列空間上にある場合、$A$ が可逆であれば
$$
\boldsymbol{x} = A^{-1} \boldsymbol{b} \tag{3.2.1}
$$
によって簡単に解が得られる（逆行列 $A^{-1}$ の計算は簡単でないかもしれないが）。$A$ が可逆ということは、$A$ は正方行列（$n \times n$ とする）でしかも正則行列（$A$ はフルランク）ということである。フルランクの正方行列では行空間も列空間も $\mathbb{R}^n$ で、零空間も左零空間も $\lbrace \boldsymbol{0} \rbrace$ なので、当然 $\boldsymbol{b}$ は列空間上にある。

3.3 入力空間内での射影

Fig.5 を見ると、方程式(3.1.1)は、入力空間内での任意のベクトル $\boldsymbol{x}$ を行空間と零空間に射影して、本質的には、射影された行空間上のベクトル $\boldsymbol{x}_R$ の $A$ による像が $\boldsymbol{b}$ であるという方程式、すなわち $A \boldsymbol{x}_R = \boldsymbol{b}$ を解いているように見える。そして、こうして求めた $\boldsymbol{x}_R$ に「報われない」零空間上の任意のベクトル $\boldsymbol{x}_N \in N(A)$ を加えたものがすべて(3.1.1)式の解になる。

そこで、入力空間内での任意のベクトル $\boldsymbol{x}$ を行空間と零空間に射影する行列をそれぞれ $P_R, P_N$ とすると

\begin{equation}\begin{split}
P_R \boldsymbol{x} &= \boldsymbol{x}_R \\
P_N \boldsymbol{x} &= \boldsymbol{x}_N \\
\end{split}\end{equation}
\tag{3.3.1}

と表され、これを(3.2.1)式に代入すると

A \boldsymbol{x} = A P_R \boldsymbol{x} + A P_N \boldsymbol{x} = A (P_R + P_N) \boldsymbol{x} = \boldsymbol{b} \tag{3.3.2}

となる。$A P_N \boldsymbol{x} = A \boldsymbol{x}_N = 0$ であるから、(3.3.2)式は

A \boldsymbol{x} = A P_R \boldsymbol{x} = \boldsymbol{b} \tag{3.3.3}

となり、これから

A = A P_R \tag{3.3.4}

という関係が得られる。この関係式を見て @osawat さんは、行列 $A$ には行空間への射影 $P_R$ が含まれるのではないかと言った。私はむしろ $A$ に $P_R$ が含まれるというよりは $P_R$ が $A$ のフィルターあるいはマスクになっており、$A$ の機能のうち行空間から列空間への写像の部分だけを取り出すような役割をしているのではないかと思っている。そのあたりの理由は具体例とともに @osawat さんのブログ ²⁾ のコメントに書いた。

いずれにせよ、行列 $A$ は、その本質は行空間から列空間への写像であり、行空間上にない任意の入力空間上のベクトル $\boldsymbol{x}$ を $P_R$ で行空間上の $\boldsymbol{x}_R$ に射影してから（つまり、報われない零空間上のベクトル $\boldsymbol{x}_N$ を削ぎ落してから） 列空間上のベクトル $\boldsymbol{b}$ へ写像するという描像を描くことができる。

コラム： @osawat さんのブログへのコメント
いま、$a, b$ を任意の $0$ でない実数として

A = \begin{bmatrix}1 & a 
\\ b& ab\end{bmatrix} 

とすると、$A$ の行空間および零空間の射影行列 $P_R, P_N$ は

\begin{equation}\begin{split}
P_R &=  \frac{1}{1+a^2}\begin{bmatrix}1&a\\a&a^2\end{bmatrix}, \\
P_N &=  \frac{1}{1+a^2}\begin{bmatrix}a^2&-a\\-a&1\end{bmatrix}
\end{split}\end{equation}

となる。
次に、$A, P_R, P_N$ を対角化すると

\begin{equation}\begin{split}
&\begin{bmatrix}1&-a\\b&1\end{bmatrix}^{-1} A \begin{bmatrix}1&-a\\b&1\end{bmatrix} =
\begin{bmatrix}1+ab&0\\0&0\end{bmatrix} \\
&\begin{bmatrix}1&-a\\a&1\end{bmatrix}^{-1} P_R \begin{bmatrix}1&-a\\a&1\end{bmatrix} =  
\begin{bmatrix}1 &0\\0&0\end{bmatrix}  \\
&\begin{bmatrix}1&-a\\a&1\end{bmatrix}^{-1} P_N \begin{bmatrix}1&-a\\a&1\end{bmatrix} =  
\begin{bmatrix}0 & 0\\ 0 & 1\end{bmatrix} 
\end{split}\end{equation}

となり、対角化後の $P_R$ は $A$ の第一列を取り出す行列になっているが、対角化後の $A$ は第一列のみの行列なので $P_R$ をかけても変わらない。つまり、$A P_R=A$ である。
同様に、$P_N$ は第二列を取り出す行列になっているが、対角化後の $A$ の第二列は $0$ なので、$P_N$ をかけた結果は $0$ になる。つまり、$AP_N=0$ である。

3.4 四大陸のメタファ

ここに至ってやっと四大陸のメタファに言及できる。ある大手旅行会社が画期的な旅行パッケージを企画した。それは太平洋上の島（ただし日付変更線以西の島とする）から北アメリカ大陸の都市へ向かう定額パッケージである。
ただし、この旅行パッケージには次のようなルールがある。それは、太平洋上の島から必ずアジア大陸の最寄りの都市を経由してから北アメリカ大陸の都市へ向かわなければならないというルールである。その際、太平洋上のその島から最寄りのアジア大陸の都市を結ぶ直線上にあれば（ただし日付変更線を東に越えてはならない）どんな島であってもパッケージ価格は同じである。ただし、当然のことながら、経由するアジア大陸の都市や目的地である北アメリカ大陸の都市が異なれば、パッケージ価格はそれに応じて変わる。

一例として、グァム島から最寄りのアジア大陸の都市である東京を経由してニューヨークへ向かうプランをFig.6に示す（東京がアジア大陸の都市であるかどうか、また、グァム島の最寄りの都市であるかどうかは甚だ疑問だが、ここではそのような細かいことは言わないことにする）。このパッケージでは東京からグァム島に引いた延長線上にある島、たとえばラバウル島を出発点に変更しても料金は同じなのだ。実のところ、島 $\boldsymbol{x}$ からアジア大陸の最寄りの都市 $\boldsymbol{x}_R$ までの運賃はこの旅行会社にとって「報われない」サービスになっている。

したがってこの場合、方程式 $A \boldsymbol{x} = \boldsymbol{b}$ を解くことは、出発点の太平洋上の島 $\boldsymbol{x}$ と目的地の北アメリカ海陸上の都市 $\boldsymbol{b}$ が与えられている状況で、アジア大陸上の最寄りの中継都市 $\boldsymbol{x}_R$ を求めることに相当する。旅行プランナーの腕の見せどころである。

3.5 右辺の b が列空間上にない場合

右辺の $\boldsymbol{b}$ が列空間上にない場合、(3.1.1)式の解は存在しない。それでも、この方程式の近似解を求めることに意味を見出だせる場合がある。この節では、まず、近似解の求め方を述べ、次にこれがどのような場合に役立つかを説明しよう。

(2.6.1)式に示したように、出力空間 $W$ 上の任意のベクトル $\boldsymbol{b} \in \mathbb{R}^m$ は、列空間 $C(A)$ 上のベクトル $\boldsymbol{p}$ と左零空間 $N(A^T)$ 上のベクトル $\boldsymbol{e}$ の和に分解でき

\boldsymbol{b} = \boldsymbol{p} + \boldsymbol{e} \tag{3.5.1}

と表すことができる（Fig.7）。

(3.1.1)式 $A \boldsymbol{x} = \boldsymbol{b}$ の近似解を $\boldsymbol{\hat{x}}$ とすると、$A$ による $\boldsymbol{\hat{x}}$ の像は $\boldsymbol{b}$ に最も近い列空間上のベクトルになるだろう。それは、$\boldsymbol{b}$ を列空間上に射影した $\boldsymbol{p}$ である。したがって

\boldsymbol{p} = A \boldsymbol{\hat{x}} \tag{3.5.2}

である。(3.5.2)式の両辺に左から $A^T$ を掛けると

A^T \boldsymbol{p} = A^T A \boldsymbol{\hat{x}} \tag{3.5.3}

となるが、これに(3.5.1)式を $\boldsymbol{p}$ について解いて得られる $\boldsymbol{p} = \boldsymbol{b} - \boldsymbol{e}$ を代入すると

A^T (\boldsymbol{b} - \boldsymbol{e}) = A^T A \boldsymbol{\hat{x}} \tag{3.5.4}

が得られる。$\boldsymbol{e}$ は左零空間上のベクトルなので $A^T \boldsymbol{e} = 0$ であるから、(3.5.4)式は

A^T \boldsymbol{b} = A^T A \boldsymbol{\hat{x}} \tag{3.5.5}

となる。
ここで、$A^T A$ が可逆である場合を考えよう。その場合、(3.5.5)式の両辺に左から$(A^T A)^{-1}$ を掛けることにより

\boldsymbol{\hat{x}} = (A^T A)^{-1} A^T \boldsymbol{b} \tag{3.5.6}

と近似解 $\boldsymbol{\hat{x}}$ を求めることができる。

さて、(3.5.6)式を求めるときに $A^T A$ の可逆性を仮定したが、そのためには

\mathrm{rank}(A) = n \le m \tag{3.5.7}

であることが必要とされる。つまり、行列 $A$ のランクはその列数 $n$ に等しく、行数 $m$ は列数 $n$ 以上でなければならない（証明はコラム参照）。Fig.7において行空間の次元が $n$ で零空間の要素が $\boldsymbol{0}$ しかないのはこのためである。

コラム：$A^T A$ が可逆であるために必要な条件
$A^T A$ は $n \times n$ の正方行列で、可逆であることから正則行列である。つまり、 $\mathrm{rank}(A^T A) = n$ である。一方、 行列の積のランクは、 積を構成するそれぞれの行列のランク以下なので $$\mathrm{rank}(A^T A) \le \min(\mathrm{rank}(A^T), \mathrm{rank}(A))$$ である。さらに、転置行列のランクは、元の行列のランクに等しいので $\mathrm{rank}(A^T) = \mathrm{rank}(A)$ であるから、最終的に $$n = \mathrm{rank}(A^T A) \le \mathrm{rank}(A) \le \min(m, n)$$ を得る。なお、上式の最後の不等号は、$m \times n$ 行列 $A$ のランクは高々行数 $m$ か列数 $n$ であるという事実を反映したものである。
もし $m \lt n$ であれば、上記の不等式は $n \le \mathrm{rank}(A) \le m \lt n$ となって不適切な不等式になる（$n \lt n$ になる）。したがって $n \le m$ でなければならず、その場合、上記の不等式は $n \le \mathrm{rank}(A) \le n \le m$ となって(3.5.7)式が得られる。

3.6 重回帰分析

前節では $\boldsymbol{b}$ が列空間にない場合に(3.1.1)式の近似解 $\boldsymbol{\hat{x}}$ を求めた。これを受けて本節ではどのような場合にこの近似解が役に立つか議論する。

ある旅行会社が、自社が企画して販売する旅行パッケージの過去の販売実績から今後企画するパッケージの販売数を予測するモデルを開発することになった。その際、販売数（$Y$ 個）は、パッケージの価格（$X_1$ 円）、旅行日数（$X_2$ 日）、 移動距離（$X_3$ km）、・・・との関係性によって決まると考え、

Y = \alpha_1 X_1 +  \alpha_2 X_2 + \cdots +  \alpha_n X_n \tag{3.6.1}

というモデルを立てた。ここで、$Y, X_1, \dots, X_n$ は平均化しているものとする（たとえば $Y$ は販売数そのものではなく、過去の販売実績の平均からのずれを表す）。これはいわゆる重回帰分析と呼ばれるもので、$Y$ を目的変数、$X_1, \dots, X_n$ を説明変数、そして $\alpha_1, \dots, \alpha_n$ を回帰係数という。

$i$ 番目の旅行パッケージの目的変数 $Y$ の値を $y_i$、説明変数 $X_1, \dots, X_n$ の値をそれぞれ $x_{i,1}, \dots, x_{i,n}$ とすると、(3.6.1)式は

\begin{bmatrix}y_1 \\ \vdots \\ y_m \end{bmatrix}
=
\begin{bmatrix}
x_{1,1} & \cdots & x_{1,n} \\ 
\vdots & \ddots & \vdots \\ 
x_{m,1} & \cdots & x_{m,n} \\ 
\end{bmatrix}
\begin{bmatrix}\alpha_1 \\ \vdots \\ \alpha_n \end{bmatrix}
\tag{3.6.2}

と行列を使って表すことができる。ここで、$m$ はパッケージ数である。

いま、

\begin{equation}\begin{split}

\boldsymbol{b} &= \begin{bmatrix}y_1 \\ \vdots \\ y_m \end{bmatrix}, \\
A &=
\begin{bmatrix}
x_{1,1} & \cdots & x_{1,n} \\ 
\vdots & \ddots & \vdots \\ 
x_{m,1} & \cdots & x_{m,n} \\ 
\end{bmatrix}, \\
\boldsymbol{x} &= 
\begin{bmatrix}\alpha_1 \\ \vdots \\ \alpha_n \end{bmatrix}

\end{split}\end{equation}
\tag{3.6.3}

とおけば、(3.6.2)式は(3.1.1)式と同じく

\boldsymbol{b} = A \boldsymbol{x} \tag{3.6.4}

という形になる。

重回帰分析では、過去の実績データ $A, \boldsymbol{b}$ から前節で導いた(3.5.6)式

\boldsymbol{\hat{x}} = (A^T A)^{-1} A^T \boldsymbol{b} \tag{3.6.5}

を用いて回帰係数 $\boldsymbol{\hat{x}}$ を求め、次いで、これも前節で導いた(3.5.2)式を使って目的変数 $\boldsymbol{b}$ の近似値 $\boldsymbol{\hat{b}}$ である $\boldsymbol{p}$（重回帰分析では近似値ではなく推測値と呼ぶ）

\boldsymbol{\hat{b}} \equiv \boldsymbol{p} = A \boldsymbol{\hat{x}} =A (A^T A)^{-1} A^T \boldsymbol{b} \tag{3.6.6}

を求めることが主要な仕事になる。

コラム：最小二乗法と射影の関係
(3.6.6)式は $\boldsymbol{b} \in \mathbb{R}^m$ を列空間上へ射影して $\boldsymbol{p}$ を求めていると見ることができ、射影演算子 $P_C$ を $$P_C \equiv A (A^T A)^{-1} A^T$$ と定義すれば $\boldsymbol{p} = P_C \boldsymbol{b}$ と書くことができる。つまり、目的変数 $\boldsymbol{b}$ の推測値 $\boldsymbol{\hat{b}} = \boldsymbol{p}$ を求めることは $\boldsymbol{b}$ を列空間上に射影することと等価である。
一方で、重回帰分析は目的変数と推測値の誤差 $\boldsymbol{b} - \boldsymbol{\hat{b}} = \boldsymbol{b} - \boldsymbol{p} = \boldsymbol{e}$ の絶対値の二乗 $|\boldsymbol{e}|^2$ を最小化するいわゆる最小二乗法によって予測を行う手法として理解されているが、ここで見たように最小二乗法と射影は同等な数学的操作であることがわかる。
このように同じ数学的操作を異なる観点から眺めると不思議な感じがするとともに線形代数の奥深さを垣間見た気がする。

3.7 直行便がない！

アジア大陸の都市 $\boldsymbol{x} \in C(A^T)$ から大西洋上に浮かぶバミューダ諸島 $\boldsymbol{b}$ へ行きたいのだが直行便がない（$A \boldsymbol{x} = \boldsymbol{b}$ ?）。そんな場合どうすればよいだろうか。幸いアジア大陸 $C(A^T)$ の各都市から北アメリカ大陸 $C(A)$ の都市に向かう航空路はいくつもある（Fig.8）。

もっとも効率がよいのは最終目的地であるバミューダ諸島 $\boldsymbol{b}$ の最寄りの北米大陸の都市 $\boldsymbol{p}$ を探してそこへの直行便があるアジア大陸の都市 $\boldsymbol{\hat{x}}$ を出発点にすればよいだろう（$A \boldsymbol{\hat{x}} = \boldsymbol{p}$）。実際はどうか知らないが、バミューダ諸島 $\boldsymbol{b}$ の最寄りの北米大陸の都市 $\boldsymbol{p}$ がニューヨーク、（他にもたくさんあるだろうが）そこへの直行便があるアジア大陸の都市 $\boldsymbol{\hat{x}}$ が東京であるとして描いたのが Fig.8 である。

この場合、ニューヨーク $\boldsymbol{p}$ はバミューダ諸島 $\boldsymbol{b}$ の近似値になっており、北米大陸からの誤差（$\boldsymbol{e} = バミューダ諸島 \boldsymbol{b} - ニューヨーク \boldsymbol{p}$）が最小化されている。つまり、この旅行プランは最小二乗法プランである。

4. おわりに

ストラング先生の４つの部分空間を４大陸になぞらえて解説記事を書いてみようというアイデアは良かったのだが、こうして書き終えてみると４大陸の話がほとんどなかったし、加えて４大陸を持ち出す必然性が感じられなかった。つまり、４大陸になぞらえて理解が深まった、あるいは理解が助けられたという実感が少しもわかない。

ということで企画倒れになってしまったが、記事を書いている身にとってはどのようなメタファにしようかとあれこれ考えているときは楽しかったし、そのお陰で４つの部分空間に親近感が湧いた。しかし、所詮、メタファはメタファである。読者は話半分程度に受け取って読んで欲しい。

なお、４つの部分空間の解説も @kenjihiranabe さんの Qiita の記事 ⁵⁾ の焼き直しのようになってしまい、あまり新鮮味はなかった。しかし、最初はあまり理解していなかったストラング先生の４つの部分空間が今ではすっかり分かったような気になれたのは良かったと思う。

参考文献

1. G. ストラング：線形代数イントロダクション 原著第４版. 近代科学社, 2015.
2. @osawat：ストラング先生の4つの部分空間 （行空間と零空間）. https://qiita.com/osawat/items/380ea7b8f424030efa0b, （閲覧日：2024.3.5）
3. データ分析を楽しむ会：Gストラング線形代数勉強会. https://study-data-analysis.connpass.com/event/311877/, （閲覧日：2024.3.5）
4. @kenjihiranabe (平鍋 健児)：Ax=b を4つの部分空間を使って理解する?連立一次方程式の解の秘密?. https://qiita.com/kenjihiranabe/items/51a7f45e4972339e2aa3, （閲覧日：2024.3.10）
5. @kenjihiranabe (平鍋 健児)：線形代数学の基本定理 - 4つの部分空間. https://qiita.com/kenjihiranabe/items/eadbcae5402d89660e65, （閲覧日：2024.3.5）