これは何?
- Gilbert Strang 先生から学んだ線形代数シリーズ、第3回目の記事です。全体は以下から。
前回、行列 $A$ の「4つの部分空間」について導入しました。
今回は、このコンセプトを使って、連立一次方程式 $Ax=b$ の解の構造について見ていきたいと思います。
問題
こんな連立方程式を考えます。
\begin{align}
2x+2y+4z &= 4 \\
4x+4y+8z &= 8 \\
x+2y+3z &= 2
\end{align}
これを行列の言葉で書くと、
\begin{bmatrix}
2 & 2 & 4 \\
4 & 4 & 8 \\
1 & 2 & 3 \end{bmatrix}
\begin{bmatrix}
x \\ y \\ z
\end{bmatrix}
= \begin{bmatrix}
4 \\ 8 \\ 2
\end{bmatrix}
こうなり、さらに、 $x, y, z$をそれぞれ$x_1, x_2, x_3$ としてベクトル行列表記すると、短く、
Ax = b \\
と書くことができます。一般化すると、$n$個の変数からなる実数係数の$m$本の一次式からなる「連立一次方程式」を解くということになります。さらに、見方を変えて、ベクトル $x \in \mathbb{R}^n$に行列 $A$ ($m \times n$) を掛け、$\mathbb{R}^m$に写像したときに、ベクトル $b \in \mathbb{R}^m$となる $x$ を求める問題です。
$m=n$ の場合、1つの解が求まることも多いですが、$m \gt n$の場合は解がないこともありますし、$m \lt n$ の場合は解が複数あることもあります。「多い」とか「場合がある」とか、はっきりしない言い方ですよね。この辺りを正確に表現しよう、というのがテーマです。
例に挙げた式をよくみると、1行目を2倍したものが2行目になっているので、条件の情報量としては2つ式だけです。見た目は3本の式と3個の変数ですが、どうも条件がゆるそうです。この方程式の解はどのようになるでしょう? 一般的な視点でその構造を解き明かしていきたいと思います。
答えを先に
線形代数に慣れた方のために、先に結論を貼っておきます。この図が「読めれば」ここから先に新しい情報はありません。

図: $Ax = b$ の構造
Ax=b の構造
さて、$y=Ax$ によって $\mathbb{R}^n$ から $\mathbb{R}^m$ への線型写像 $f$ が定義され、$A$から自然に以下の4つの部分空間が定義されることは、前回述べました。この上に、今回の問題を重ねて描きます。
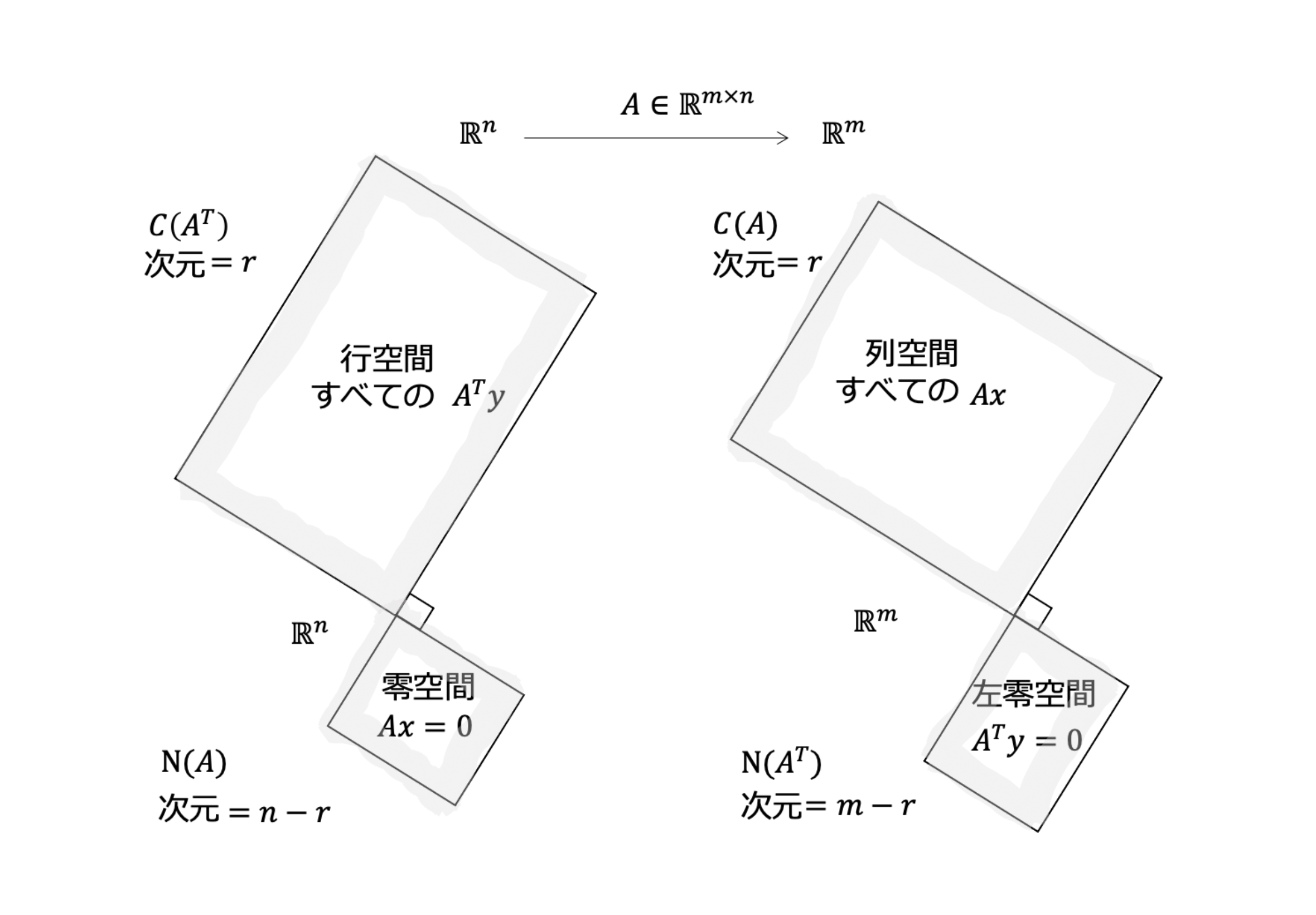
図: 世界標準MIT教科書 ストラング:線形代数イントロダクションより(前回から再掲)
Axの2つの見方
まず、この方程式に解があるかどうか、を考えます。左辺には2つの見方があったことを思い出してください。
\begin{align}
Ax &= b \\
\begin{bmatrix}
2 & 2 & 4 \\
4 & 4 & 8 \\
1 & 2 & 3 \end{bmatrix}
\begin{bmatrix}
x_1 \\ x_2 \\ x_3
\end{bmatrix}
&= \begin{bmatrix}
4 \\ 8 \\ 2
\end{bmatrix}
\end{align}
- 行ごとに式を内積として見る
Ax = \begin{bmatrix}
2x_1+2x_2+4x_3 \\
4x_1+4x_2+8x_3 \\
x_1+2x_2+3x_3
\end{bmatrix}
この見方では、3つの式は3つの内積とそれぞれの値、という風に見えます。問題は、3つの行ベクトルと内積を取って $b$ のそれぞれの値になる$x$を求めよ、という意味になります。図形的には、3つの平面の交点を求める、とも読めます。
- 列ベクトルの線型結合として見る
Ax = x_1 \begin{bmatrix} 2 \\ 4 \\ 1 \\ \end{bmatrix}
+ x_2 \begin{bmatrix} 2 \\ 4 \\ 2 \end{bmatrix}
+ x_3 \begin{bmatrix} 4 \\ 8 \\ 3 \end{bmatrix}
こちらの見方では、全部で1つの式と見た方がよいでしょう。問題は、3つの列ベクトルの線型結合が、与えられた $b$ になるように係数 $x_1, x_2, x_3$ を見つけよ、という意味になります。図形的には、3つのベクトルをそれぞれ何倍かして足し合わせ、求めるベクトルにする、とも読めます。
こんなビジュアルを頭に焼き付けると、すぐにこの2つの解釈が見えるようになります。
解が存在するかどうか
ここでは、左の見方(3つの内積)から、右の見方(3つの列ベクトルの線型結合)へと移行します。取りうるすべての$x$に対しての $Ax$ の集合が列空間 $C(A)$ でした。その中の1つが今回指定された $b$ と等しい必要があるので、
- $Ax=b$に解がある $\Leftrightarrow$ $A$ の列空間 $C(A)$ に $b$ が存在する。
なのです。そうすると、図の中の $b$ の位置によって解の有無が決まります。$b$を$\mathbb{R}^m$内にプロットして$C(A)$の中に入っているかどうか、が決め手です。
ところで、他の教科書だと、$A$を拡張して $[A | b]$ という $m \times (n+1)$ 行列を作り、
- $Ax=b$ に解がある $\Leftrightarrow$ $\mathrm{rank} A = \mathrm{rank} [A | b]$
と書いてあるものが多いですが、実はランクを調べる変形操作の中で、 $b \in C(A)$ すなわち、$Ax$ が $b$ に到達可能かを調べていたのです。
もう一度。
- $Ax=b$に解がある $\Leftrightarrow$ $b \in C(A)$
解は1つか
次に、解がある場合に、複数あるか?という問題です。ある解が既に1つ見つかったとします。これを特解 (particular solution) と呼んで、$x_p$ とします。
Ax_p = b
また、 $Ax = 0$ の解を零解(null solution)と呼び、 $x_n$ と書きます。
Ax_n = 0
この $x_n$ が $0$ 以外に存在すれば、$x=x_p + x_n$ も必ず解(別の解)となります。複数の解がこれで作れます!
Ax = A(x_p + x_n) = Ax_p + Ax_n = b + 0 = b
さあ、ここでピンときますよね、複数の解を持つには、$x_n \ne 0$ が存在すればいいのです。$x_n$ は4つの部分空間のどこに存在するでしょう? $Ax = 0$ の解($x_n$)すべてを構成する空間を私たちは知っています。そう、零空間 $N(A)$ です。ですから、解が複数あるかどうかの判断の決め手はこれ。
- $Ax=b$ に解が複数ある $\Leftrightarrow$ 解が1つ存在し、かつ、$ \{ 0 \} $ でない零空間 $N(A)$ が存在する
ということになります。最初に1つの解の存在を言ったのは、$Ax =b$ を満たす $x_p$ がまず1つ無ければ、0 をいくつ足しても $b$ には届かないからです。
$x_n$ は $N(A)$ 部分空有間にたくさん存在するので、一つでも$x_n$が存在すれば自動的に解は無限にある、ということになります(ちょうど2つある、ということは起こり得ません)。少なくとも、$x_n$ の定数倍はすべて $N(A)$ に属するので、すでに無限です。もう少し踏み込むと、 $N(A)$ の次元、 $\dim N(A)$ 個のパラータで表現されるだけ多くの解が存在します。$x_n$ として線形独立なベクトルが、$N(A)$ 内に、 $\dim N(A)$ 個取れ、それらの線形結合は、すべて $x_p$ に足しても解となるわけです。
さらに、$x_p$ は、$\mathbb{R}^n$ 内にありますが、$N(A)$ 成分とその直交成分、すなわち行空間 $C(A^T)$ 成分に分解できます。この2つの空間は互いに直交補空間となっていたことを思い出してください(直和でありそれらの和空間が全体を充満する。和空間は和集合ではなくそれぞれの空間要素の線型結合全体)。
\begin{align}
C(A^T) &\perp N(A) \\
\dim C(A^T) &+ \dim N(A) = n \\
C(A^T) &\oplus N(A) = \mathbb{R}^n
\end{align}
すべての $x$ が、$C(A^T)$と $N(A)$の和に一意に分解されるるので、$x_p$も分解可能です。その $N(A)$成分は $x_n$ですから、$C(A^T)$成分を $x_r$ とします。(row spaceの $r$ )
x_p = x_r + x_n, \qquad (x_r \in C(A^T), \quad x_n \in N(A))
これまで、$x_p$ はなんでもよく、$x_n$ を何倍かして足しても $x_p$として1つの解となりました。また、それに $x_n$をどれだけ足しても、全体の解になります。ただ、$x_p$を $x_r$に限る、というか$x_n$に直交する成分だけ残してそれを $x_r$とすれば、一意的に $x_r$ が取れます。
もう一度。
- $Ax=b$ に解が複数ある $\Leftrightarrow$ 解が1つ存在し、かつ$\{0\}$でない零空間 $N(A)$ が存在する
- 解の自由度は $\dim N(A)$である。
- 解が存在すれば、$C(A^T)$ 成分と $N(A)$ 成分の和に一意に分割される。
図で見てみよう
さて、お待たせしました。最後にこの絵で全体を理解しましょう。

図: $Ax = b$ の構造
次の順に辿ってください。
- $b$ の位置。$b'$ の位置
- 一般解 $x = x_r + x_n$
- $Ax=0$ の解 $x_n$ の位置
- 行空間の解 $x_r$ の位置
- $x_p$ はたくさん
- $A$ の緑の線が向かう3つの先
- $N(A)$ の大きさ
この図がとてもうまく説明に機能することが分かりますよね!
消去法との関係
では、Gauss の消去法もしくは行基本変形による解き方をここで再現し、より理解度を高めたいと思います。
\begin{bmatrix}
2 & 2 & 4 \\
4 & 4 & 8 \\
1 & 2 & 3 \end{bmatrix}
\begin{bmatrix}
x_1 \\ x_2 \\ x_3
\end{bmatrix}
= \begin{bmatrix}
4 \\ 8 \\ 2
\end{bmatrix}
を消去で解いていきます。変形は行基本変形であり、行空間および零空間は変化しません。なぜなら、連立方程式を辺々足したり引いたりしているだけですから、行の張る空間(行空間)および連立方程式の解(零空間)は変化しません。でも、列空間側はどんどん変わっていきます!
しかし、行基本変形は「可逆な線形変換」ですから、$b$ と $C(A)$は変化しますが、「$b$ と $C(A)$ の関係」つまり、$b$ が $C(A)$ に入っているかどうか、は変わりません。
\begin{align}
& \begin{bmatrix} \begin{array}{ccc|c}
2 & 2 & 4 & 4\\
4 & 4 & 8 & 8\\
1 & 2 & 3 & 2 \\
\end{array}
\end{bmatrix}
& \begin{matrix}
① \div 2 \\
② \div 4 \\
\longrightarrow
\end{matrix}
& \begin{bmatrix} \begin{array}{ccc|c}
1 & 1 & 2 & 2\\
1 & 1 & 2 & 2\\
1 & 2 & 3 & 2 \\
\end{array}
\end{bmatrix} \\
\begin{matrix}
② - ① \\
③ - ① \\
\longrightarrow
\end{matrix}
& \begin{bmatrix} \begin{array}{ccc|c}
1 & 1 & 2 & 2\\
0 & 0 & 0 & 0\\
0 & 1 & 1 & 0 \\
\end{array}
\end{bmatrix}
& \begin{matrix}
② \leftrightarrow ③ \\
\longrightarrow
\end{matrix}
& \begin{bmatrix} \begin{array}{ccc|c}
1 & 0 & 1 & 2\\
0 & 1 & 1 & 0 \\
0 & 0 & 0 & 0
\end{array}
\end{bmatrix}
\end{align}
となります。計算大丈夫ですよね。ここで、ピボット列が 1,2 列目。自由列が 3 列目です。$x_3$ を自由変数とし、まず $x_3 = 0$ として、$x_p$を見つけます。
x_p = \begin{bmatrix}
2 \\ 0 \\ 0
\end{bmatrix}
次に、自由列にあたる $x_3 = 1$として、$Ax=0$ となる $x_n$を見つけます。
x_n = \begin{bmatrix}
-1 \\ -1 \\ 1
\end{bmatrix}
これで、みなさんが見慣れた解の一般形が書き出せます。 $s$ をパラメータとします。
x = x_p + x_n = \begin{bmatrix}
2 \\ 0 \\ 0
\end{bmatrix} + s \begin{bmatrix}
-1 \\ -1 \\ 1
\end{bmatrix}
$Ax_p=b$ および、$Ax_n=0$ を確認してください。さらに $x_r$ を見つけるのはひと手間かかりますが、これは、問題としておきましょう。
正則あるいは可逆
行列 $A$ が逆行列 $A^{-1}$ を持つ場合、正則行列、というのでした。それについてもちょっと考えてみます。
\begin{align}
A x &= b \\
x &= A^{-1}b
\end{align}
まず、この記事の議論では、$A$は $(m \times n)$行列でした。教科書では $m=n$ の場合しか $A$ は正則ではないと習うかもしれませんが、ほんとかどうかも、検証してみましょう。
まず、これは、$A$ と $b$ が決まると $x$が一意に決まる、ということを意味しています。どんな $b$ を取ってきても、$x$が存在する必要があります。そのためには、$Ax$ が到達可能な範囲に $b$がないといけないのですが、$b$に制限はないです。だから、$b$ が常に到達可能であるためには、 $b$ が存在する全空間 $\mathbb{R}^m$ が $C(A)$で埋め尽くされている必要があります。つまり、
\begin{align}
\mathbb{R}^m &= C(A) \\
N(A^T) &= \{0\}
\end{align}
が要請されます。$m, n$ の関係で言うと、
\dim C(A) = \mathrm{rank}(A) = m, \quad \dim N(A^T) = 0
次に、解が複数あってもいけません。ということは、$x_n=0$ しか認められないのです。つまり、零空間もつぶれてしまって、$N(A)= \{0\}$である必要があるのです。すると、自動的に $C(A^T)$が$\mathbb{R}^n$ を埋め尽くすことになりますね。
\begin{align}
N(A) &= \{0\} \\
\mathbb{R}^n &= C(A^T)
\end{align}
が要請されます。つまり、$m, n$ の関係で言うと、
\dim C(A^T) = \mathrm{rank}(A^T) = n, \quad \dim N(A) = 0
さらに、「行ランクと列ランクは等しい(→別記事))」を使うと、
\begin{align}
r &= \mathrm{rank} (A) = \mathrm{rank} (A^T) \\
r &= m = n
\end{align}
すなわち、Aが正則である条件は、Aが正方行列であり、
\mathrm{rank} (A) = n
と言えるのです!
さらに、さらに、$A$が$n$次正方行列でランクが$n$であれば、逆にたどって $Ax=b$がただ一つの解を持つことが言えます。(左からかける$A$と右からかける$A$の話を残しますが、$A^T$を考え、図の対称性から言えるでしょう)
問題
この記事の理解度を試す問題です。
問1
\begin{bmatrix}
2 & 2 & 4 \\
4 & 4 & 8 \\
1 & 2 & 3 \end{bmatrix}x
= \begin{bmatrix}
4 \\ 8 \\ 2
\end{bmatrix}
の解は、
x = x_p + x_n = \begin{bmatrix}
2 \\ 0 \\ 0
\end{bmatrix} + s \begin{bmatrix}
-1 \\ -1 \\ 1
\end{bmatrix}
が求まりました。ここから、行空間上の $x_r$ を求めてください。 $x=x_r+x_n$ と書くこともできます。
- ヒント1: 行空間の線型結合として $x_r$ が書けます。
- ヒント2: $x_p$ から行空間に「垂線」を下ろした足として$x_r$ が書けます。
- ヒント3: $x$ の中で最も長さの短いものが $x_r$ です。 $s$ のパラメータ表示で長さを表示し、それを最小化するものを求めてもいいでしょう。
- ヒント4: 同じ意味ですが、 $s$ で微分する、という考え方もあります。
- ヒント3: 射影行列がわかる方は、行空間への射影行列 $P$ を求めると $x_r = P x_p$ です。
問2
この解(行空間の解 $x_r$ )は、無数にある $x$ の中でノルム(長さ)が最小であることを説明してください(上記ヒント3)。
ヒント:最小であることの説明には、直角三角形3角形の辺の長さの性質(点から平面上の点への距離が一番短くなるのは垂線の足)を使ったものや、その結果として射影行列を使うもの、最小値になる条件を微分を使って求めるものがあります。
問3
一般的に $Ax=b$ の一つの解が $x_p$ の時の $x_r$ を式で書き下してください。
やり方は、上記の過程を一般的にたどることになります。ただし、$A$ のランクは列数に比べて小さく(複数解を持つ)、行空間 $C(A^T)$ の線形独立なベクトルのみ並べたものが、$C$と書けるとします。上記の問題では、$A$ の3つの行のうち1行目と2行目は線形従属なので、1行目の(1/2)倍、と3行目を線形独立なベクトルとして採用し、それらを転置したものを並べて、
C = \begin{bmatrix}
1 & 1\\
1 & 2\\
2 & 3
\end{bmatrix}
とします。これは、 $C(A^T)$ を表す行列となります(ダブりを省いています)。
この問題には答えを書いておきましょう。
x_r = C (C^T C)^{-1} C^T x_p
です。先に $C$ を単位直交行列化して $V$ とおけば、
V^T V = I\\
x_r = V V^T x_p
とも書けます。先の射影行列 $P$ は、
P = C (C^T C)^{-1} C^T = V V^T
だったということです(この問題が難しかった方に、別の射影に関する記事を書く予定です)。
本が出ました
このテーマが詳しく語られている本が日本語版が出ました(2023/2/11)
ストラング:教養の線形代数

Tシャツ作った
この話をはじめてきいたとき、あまりにも感動したので、Tシャツを作りました。

いきさつやストーリーはこちら(Tシャツの記事(英語)→)
行列の掛け算を可視化
Gilbert先生は $Ax$ を内積と線型結合の2つの見方でみるような「目の慣れ」を重視して講義を進めています。こんな可視化に興味がある方は、こちらにまとまった資料
Gilbert先生は $A$ の分解を「目の慣れ」を重視して講義を進めています。こんな可視化に興味がある方は、こちらにまとまった資料
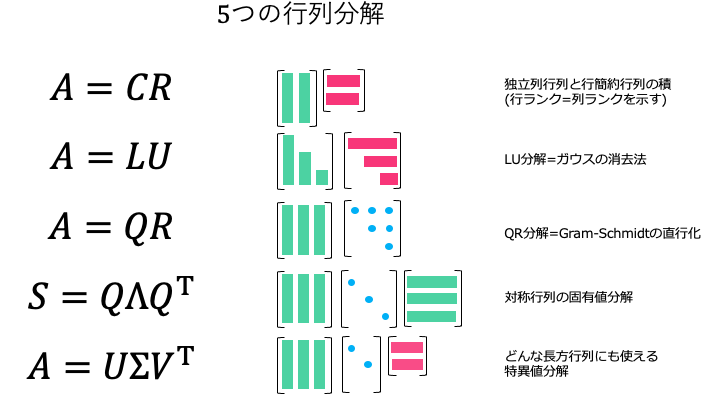
があります。私はこれを推し進めて、先生の提唱する行列5分解を、今後解説していこうと思います。5つの行列分解については、こんな感じです。
参考文献
- Gilbert 先生の他の線形代数やデータサイエンスの書籍について。(こちらの別記事)
このシリーズについて
このシリーズでは、Gilbert Strang 先生の Linear Algebra Vision 2020 を元に、この後、$LU$分解, $QR$分解(Gram-Schmidt), 固有値分解, 特異値分解(SVD) を扱っていきます。
Gilbert Strang 先生は MIT の有名な(名物)線形代数の先生です。OpenCourseware で無償で先生の講義をみることができます。 線形代数イントロダクション や 教養の線形代数(2023年) という著書があります。
今後、シリーズ化して先生の講義から目から鱗の話題を解説する予定です。
先生については、別のページで紹介します(日本語版は別途用意中)。