これは何か?
このシリーズでは、Gilbert Strang 先生の Linear Algebra Vision 2020 を元に、線形代数の直感的理解を得るための「目から鱗」の話題を紹介したいと思います。
Gilbert Strang 先生は MIT の有名な(名物)線形代数の先生です。OpenCourseware で無償で先生の講義をみることができます。これが、とっても楽しいです。定理の証明を追うようなスタイルでなく、具体的な数で手を動かしながら、どんどん、直感的理解が進みます。ほんと、目から鱗です。まるで、古典落語を鑑賞するような感覚で何度も見ることができるクラシックです。
その他、有名な著作がいくつもあり、インタビュー動画等もあります。
先生の線形代数の本
-
『ストラング:教養の線形代数』 日本語版が出ました(2023/2/11)。 表紙の $A=CR$ の意味、解説はこちらに。(→解説記事)

-
『線形代数イントロダクション』(原著: "Introduction To Linear Algebra" )表紙の意味わかりますか? 解説がこちらに。(→解説記事)

-
『線形代数とデータサイエンス』
よりデータサイエンスや機械学習に必要な要素が詳しく。

記事のリスト(執筆中)
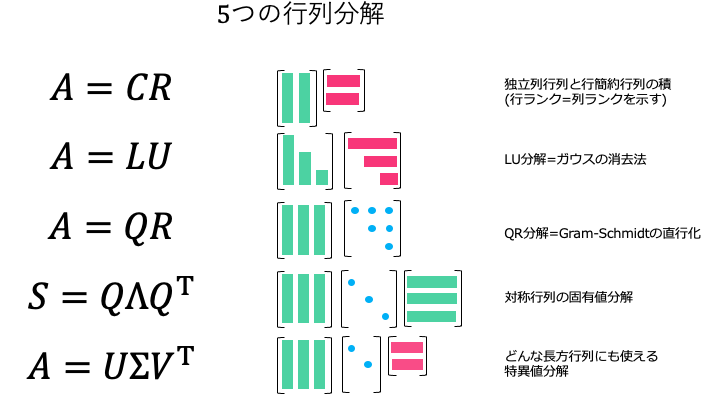
さて、という訳で以下が**「Gilbert Strang先生から学んだ線形代数」**シリーズの目次です。
- QR 分解を使ってGram-Schmidt の直交化を理解する(未稿)
- 対称行列の固有ベクトルは互いに直交する(ように選べる)(未稿)
- 特異値分解(SVD)によって任意の(長方)行列は、直交・対角・直交の3行列に分解できる(未稿)
視覚化して行列演算を捉えることに挑戦していて、こんな感じで上記を展開する予定です。
このあたりに興味がある方は、こちらに資料があります。
先生と私のエピソード
個人的に email を交換することができ、その過程で、先生の人柄にふれ感動してTシャツを作ったりしています。
- Gilbert 先生のTシャツのお話
- Matrix World の話