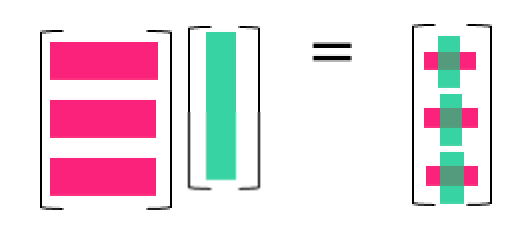これは何?
- Gilbert Strang 先生から学んだ線形代数シリーズ、第2回目の記事です。全体は以下から。
今回は、線形写像の表現行列 $A$ の「4つの部分空間」(The Four Subspaces)について、証明ではなく直感的に理解する方法について書いてみます。それらは$A$の零空間、$A$の列空間、$A$の行空間、$A$の左零空間です。
これは、『線形代数学の基本定理』とも呼ばれています。この定理には、先生の教育上の功績が大きいと思います。
- 線形代数学の基本定理 (Wikipedia) - $(m \times n)$行列 $A$ が表現する$\mathbb{R}^{n}$ から $\mathbb{R}^{m}$ への線型写像に自然に定義される、4つの部分空間の間に成り立つ関係
ザ・4つの部分空間
ここでは、実数のベクトル空間を扱います。行列 $A$ ($m \times n$) から、 $y=Ax$ によって $\mathbb{R}^n$ から $\mathbb{R}^m$ への線型写像 $f$ が定義されます。$A$から自然に以下の4つの部分空間が定義されます。
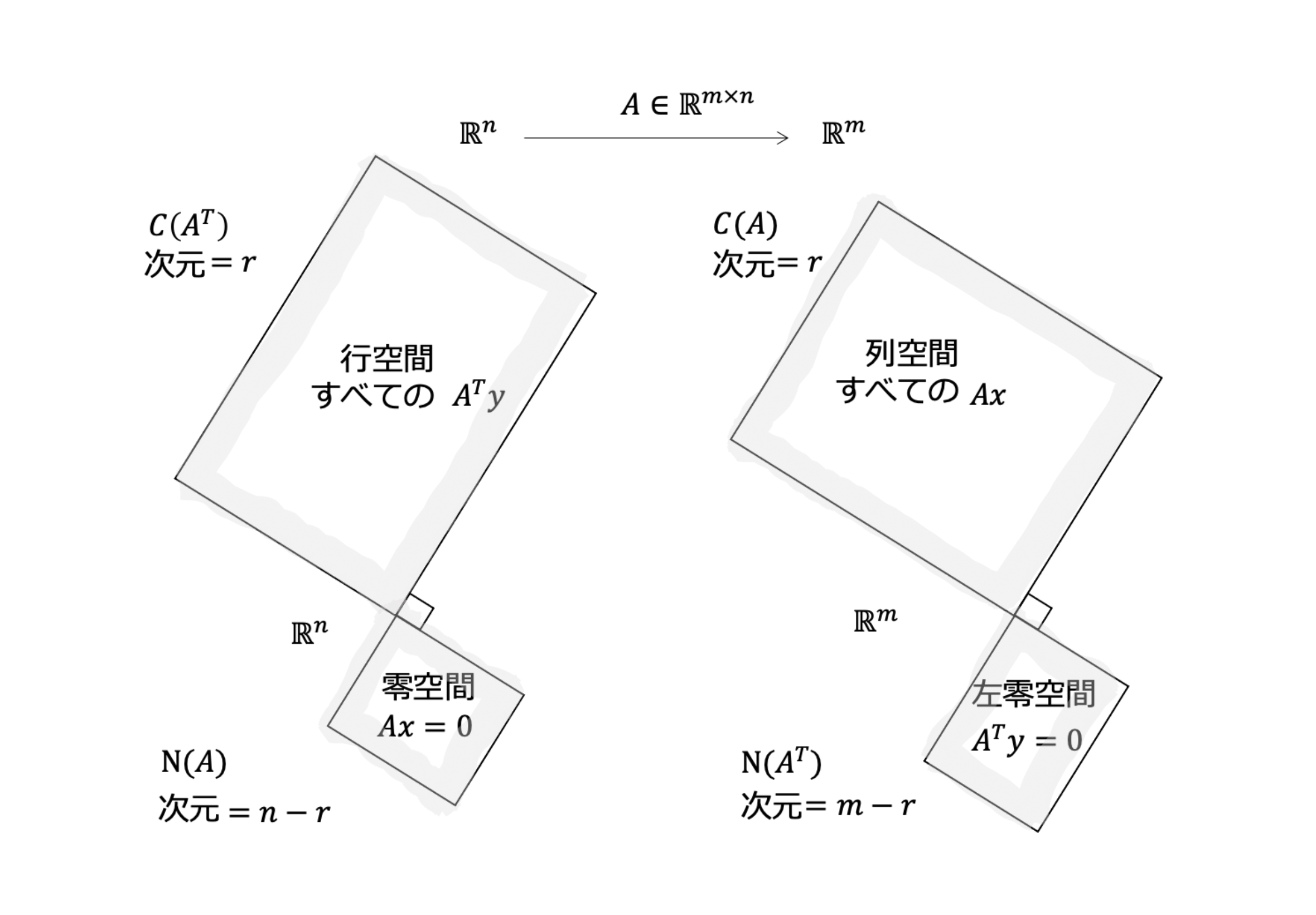
図: 世界標準MIT教科書 ストラング:線形代数イントロダクションより
$r$を$A$の階数 $r=\mathrm{rank}(A)$ として、
- 行空間 $C(A^T)$ は $\mathbb{R}^n$ の部分空間であり、次元は $r$ である。
- 列空間 $C(A)$ は $\mathbb{R}^m$ の部分空間であり、次元は $r$ である。
- 零空間 $N(A)$ は $\mathbb{R}^n$ の部分空間であり、次元は $n-r$ である。
- 左零空間 $N(A^T)$ は $\mathbb{R}^m$ の部分空間であり、次元は $m-r$ である。
上記には、
- 行空間と列空間の次元は等しい。 すなわち、$r=\mathrm{rank}(A)=\mathrm{rank} (A^T)$
が含まれています。このことについては別記事に書きました(行列の行ランクと列ランクはなぜ等しいか)。さらに、
- $\mathbb{R}^n$ において、行空間は零空間の直交補空間となる。
- $\mathbb{R}^m$ において、列空間は左零空間の直交補空間となる。
すごい!
それぞれの部分空間
Strang流に則って、具体的例示で進めます。行列 $A$ は前回の記事(行列の行ランクと列ランクはなぜ等しいか?)で使った例です。
y = Ax = \begin{bmatrix}
2 & 2 & 4 \\
4 & 4 & 8 \\
1 & 2 & 3 \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\ x_2 \\ x_3
\end{bmatrix}
という写像を考えます。ここで、 $x$が左の $\mathbb{R}^n$、$y$が右の$\mathbb{R}^n$の中に存在します。そして、$A$がその間の変換行列です。(わざと、1列目と2列目を足して3列目になるように細工してあります。)
図には、右に2つ、左に2つの部分空間がそれぞれあります。右上の列空間 $C(A)$ から初めましょう。
Ax = \begin{bmatrix}
2 & 2 & 4 \\
4 & 4 & 8 \\
1 & 2 & 3 \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\ x_2 \\ x_3
\end{bmatrix} =
(x_1)\begin{bmatrix} 2\\ 4\\ 1\\ \end{bmatrix}
+ (x_2)\begin{bmatrix} 2 \\ 4 \\ 2 \\ \end{bmatrix}
+ (x_3)\begin{bmatrix} 4 \\ 8 \\ 3 \\ \end{bmatrix}
という風にバラして見ます。このバラし方をこのように直感的に見えるように慣れておくとよいです。
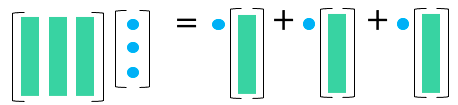
すると、$x$が $\mathbb{R}^n$ 全体(左側)を動くとき、$Ax$は、3つの列ベクトルの線型結合全体となり、$A$の列ベクトルが張る空間になります。これを、$A$の列空間と呼び、$C(A)$ と書きます。これは、 $\mathbb{R}^m$ の部分空間となります。$A$の値域(Range)とか像(Image)とも呼ばれます。記号を使ってより一般的に書くと、
A = \begin{bmatrix}
| & | & | \\
a_1 & a_2 & a_3 \\
| & | & |
\end{bmatrix}, \;
x = \begin{bmatrix}
x_1 \\ x_2 \\ x_3
\end{bmatrix}
として、
Ax=
x_1\begin{bmatrix} | \\ a_1 \\ | \\ \end{bmatrix}
+ x_2 \begin{bmatrix} | \\ a_2 \\ | \end{bmatrix}
+ x_3 \begin{bmatrix} | \\ a_3 \\ | \end{bmatrix}\\
と $a_1, a_2, a_3$の線型結合として $C(A)$が書けるので、
C(A) = \{y \in \mathbb{R}^m \mid y = Ax, x \in \mathbb{R}^n \}
と表現できます。
次に 左下の$N(A)$です。これは、$Ax=0$ となる $x$ の集合です。 $A$の零空間 とか核空間(Kernel)、0の逆像$f^{-1}(\boldsymbol{0})$ とも呼ばれ、$\mathbb{R}^n$ の部分空間です。
Ax = \begin{bmatrix}
2 & 2 & 4 \\
4 & 4 & 8 \\
1 & 2 & 3 \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\ x_2 \\ x_3
\end{bmatrix} = 0
今度はこれを、こう読みます。横ベクトルと縦ベクトルの積です。
Ax = \begin{bmatrix}
\begin{bmatrix}2 & 2 & 4\end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} \\
\begin{bmatrix}4 & 4 & 8\end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} \\
\begin{bmatrix}1 & 2 & 3\end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}
\end{bmatrix} = \begin{bmatrix}
2x_1+2x_2+4x_3 \\
4x_1+4x_2+8x_3 \\
x_1+2x_2+3x_3 \\
\end{bmatrix} = \begin{bmatrix}
0\\
0 \\
0 \\
\end{bmatrix}
この見方を視覚的に書くとこんな感じです。クロスで内積を表現しています。
N(A) = \{x \in \mathbb{R}^n \mid Ax=0 \}
と表現できます。
次に左上$C(A^T)$は、 $A$の行空間 で、$A$の行べクトル($A^T$の列ベクトル)が張る空間です。$y$ が $\mathbb{R}^m$ (右側)全体を動くとき、$A^Ty$ は、$A$ の行ベクトル(を列ベクトルとしたもの)の線型結合全体です。また、これは $\mathbb{R}^n$ の部分空間となります。$R(A)$ (Row Space of A)とも書きますが記号を節約して転置を使っています。
C(A^T) = \{x \in \mathbb{R}^n \mid x = A^Ty, y \in \mathbb{R}^m \}
最後に、右下$N(A^T)$は左零空間と名付けています。$A^T$の零空間で、 $A^Ty=0$となる $y$の集合で、$\mathbb{R}^m$ の部分空間となります。
N(A^T) = \{y \in \mathbb{R}^m \mid A^Ty=0 \}
直交する部分空間たち
零空間に含まれるすべてのベクトル$x$は、行空間に含まれるすべてのベクトルに直交します(これが、図で直交記号が入っている訳です)。なぜって、$Ax=0$ ですからね。$A$の各行 $ a^*_j$と $x$ の内積はすべて 0 です。
Ax = \begin{bmatrix}
- & a^*_1 & - \\
- & a^*_2 & - \\
- & a^*_3 & -
\end{bmatrix} x =
\begin{bmatrix}
a^*_1 x \\ a^*_2 x \\ a^*_3 x
\end{bmatrix} =
\begin{bmatrix}
0 \\ 0 \\ 0
\end{bmatrix}
$x$ は $A$ のすべての行に直交しているのです。零空間の元 $x$ と行空間の元 $A^Ty$ の内積 $x \cdot (A^Ty)$ をとると、
x \cdot (A^Ty) = x^T(A^Ty) = (Ax)^Ty = 0^Ty = 0
となることからも分かるでしょう。このことから、 零空間 $N(A)$と行空間 $C(A^T)$ は直交します。さらに、(行基本変形による行階段行列で明らかにされるピボットと自由変数の数の関係から)両空間の次元を足すと $n$ で $\mathbb{R}^n$ を充満するのです。
\begin{eqnarray}
\quad C(A^T) \perp N(A)& \\
\dim C(A^T) + \dim N(A) &= n \\
C(A^T) \oplus N(A) &= \mathbb{R}^n
\end{eqnarray}
まったく同様の直交性と次元関係が $\mathbb{R}^m$側の列空間と左零空間についても言えます。
\begin{eqnarray}
\quad C(A) \perp N(A^T)& \\
\dim C(A) + \dim N(A^T) &= m \\
C(A) \oplus N(A^T)&= \mathbb{R}^m
\end{eqnarray}
美しい!
今回の例では
今回の例、
A = \begin{bmatrix}
2 & 2 & 4 \\
4 & 4 & 8 \\
1 & 2 & 3 \\
\end{bmatrix}
に対応する空間を図の中に書いておきます。もしAが正則(可逆)であれば、左右の零空間は ${0}$となってつぶれています。つまり、$A$には$A^{-1}$が存在し、全単射となるわけです。今回は、3つ目の列ベクトルが $a_3 = a_1 + a_2$ となっていて$A$のランクは2です。残りの1次元(直交補空間)が、それぞれの零空間に配置されます。
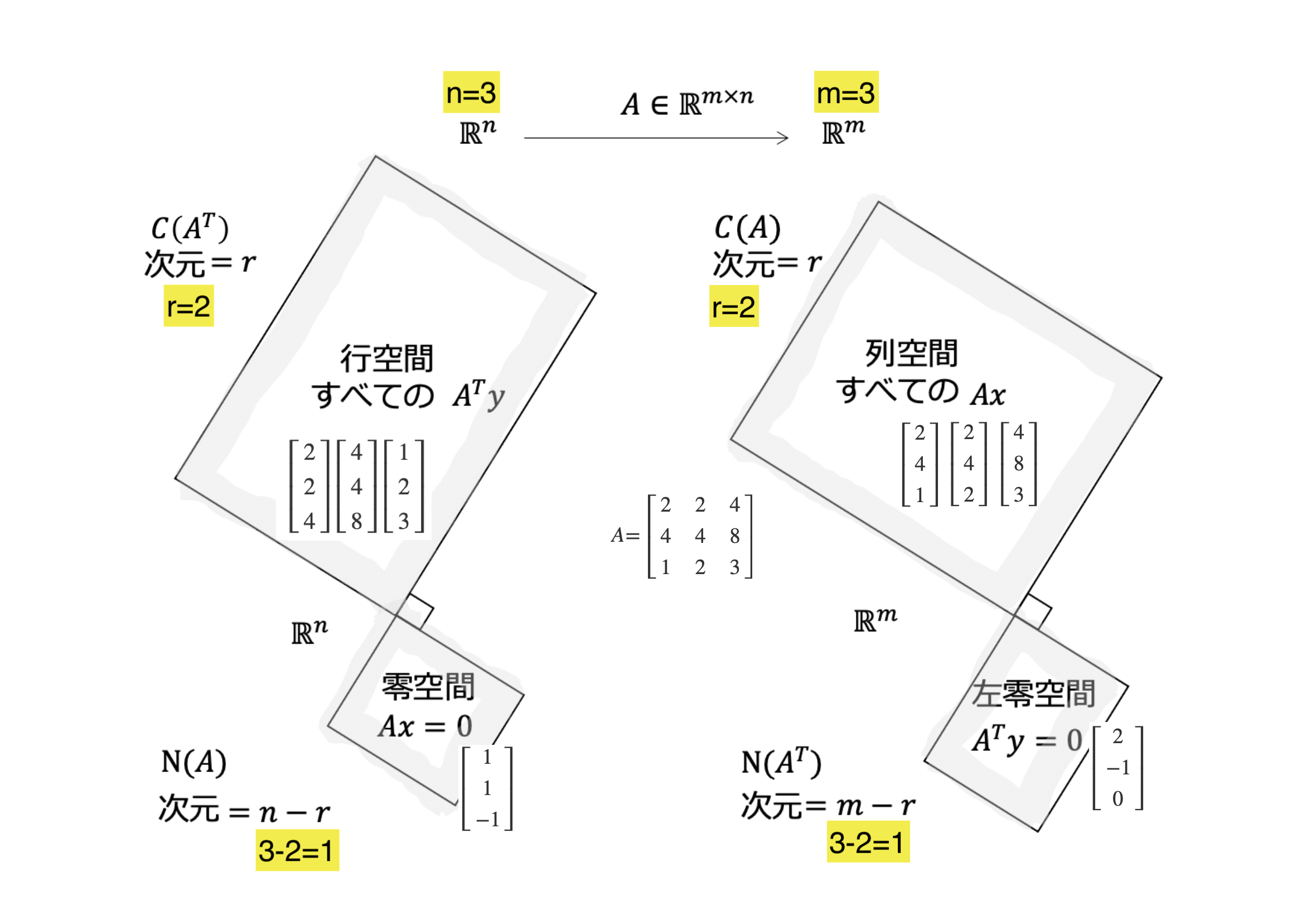
零空間のベクトルが行空間と、左零空間のベクトルが列空間と直交していることを計算で確かめてください。
Ax = \begin{bmatrix}
\begin{bmatrix}2 & 2 & 4\end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} \\
\begin{bmatrix}4 & 4 & 8\end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} \\
\begin{bmatrix}1 & 2 & 3\end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}
\end{bmatrix} = \begin{bmatrix}
2x_1+2x_2+4x_3 \\
4x_1+4x_2+8x_3 \\
x_1+2x_2+3x_3 \\
\end{bmatrix} = \begin{bmatrix}
0\\
0 \\
0 \\
\end{bmatrix}
から、
x=\begin{bmatrix}
1 \\
1 \\
-1 \\
\end{bmatrix}
が零空間 $N(A)$の基底にとれ、
A^Ty=\begin{bmatrix}
2y_1+4y_2+y_3 \\
2y_1+4y_2+2y_3 \\
4y_1+8y_2+3y_3 \\
\end{bmatrix} = \begin{bmatrix}
0\\
0 \\
0 \\
\end{bmatrix}
から、
y=\begin{bmatrix}
2 \\
-1 \\
0 \\
\end{bmatrix}
が左零空間 $N(A^T)$ の基底にとれます。
まとめ
| 名前 | 記号 | 全体空間 | 英語 | 意味 | 他の書き方 |
|---|---|---|---|---|---|
| 列空間 | $C(A)$ | $\mathbb{R}^m$ | Column Space of $A$ | すべての $Ax$ すなわち $A$ の各列ベクトルが張る空間 | $\mathrm{Image}(A), \mathrm{Range}(A), f(\mathbb{R}^n)$ |
| 零空間 | $N(A)$ | $\mathbb{R}^n$ | Nullspace of $A$ | $Ax = 0$ となる $x$ の空間 | $\mathrm{Ker}(A), f^{-1}(0)$ |
| 行空間 | $C(A^T)$ | $\mathbb{R}^n$ | Row Space of $A$ | すべての $A^Ty$ すなわち $A$ の各行ベクトル($A^T$の列ベクトル)が張る空間 | $\mathrm{Image}(A^T), f^{-1}(\mathbb{R}^m)$ |
| 左零空間 | $N(A^T)$ | $\mathbb{R}^m$ | Nullspace of $A^T$ | $A^Ty=0 $ となる $y$ の空間 | $\mathrm{Ker}(A^T)$ |
ここから何が言える?
この記事とは別に、行列の列ランクと行ランクが等しいこと、すなわち、
\dim C(A) = \dim C(A^T) = \mathrm{rank}(A)
が言えます。(詳しくはこの記事を参照してください)
さらに、零空間と行空間が$ \mathbb{ R }^n $を構成する直和となっていること、
n = \dim C(A^T) + \dim N(A)
この二つから、
n = \dim C(A) + \dim N(A)
が導かれます。
もしくは写像の言葉で、$A$ によって表される $ \mathbb{ R }^n $ から $ \mathbb{ R }^m $への線形写像を $f$ 、とすると、その核空間 $f^{-1}(\boldsymbol{0}) $ と値域 $f(\mathbb{ R }^n) $の次元には、
n = \dim f(\mathbb{ R }^n) + \dim f^{-1}(\boldsymbol{0})
の関係が成り立つというのが線形代数の第一のハイライトです。
他の教科書では...
- 『ストラング:教養の線形代数(2023新刊)』 日本語版が出ました(2023/2/11)。

この記事は、この本の議論に沿って解説しています。(表紙の $A=CR$ の意味、解説はこちらに→解説記事)。もう一冊先生の本です。
図: 森毅 『線型代数〜生態と意味』より
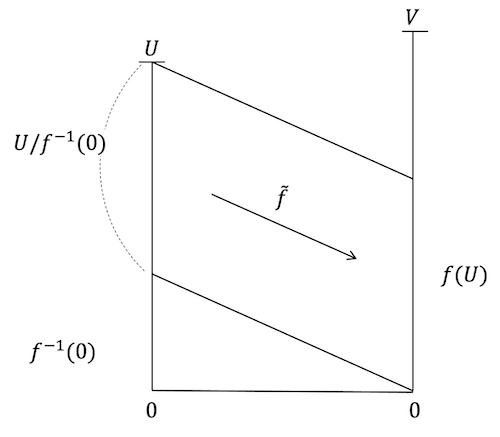
この議論を「線型写像の標準分解」と呼んでいます。定義域全体を$U$、$f$の零空間を $f^{-1}(0)$ として行空間を商空間$U/f^{-1}(0)$としてみています。また、$f$ を制限した双射 $\tilde{f}$ を作ることによって、
\dim U/f^{-1}(0) = \dim \tilde{f} = \dim f(U)
を示します。また、$\dim U/f^{-1}(0)$ を零空間の "余次元 $\mathrm{codim}$ " と呼んでいます。そして、余次元の性質
\mathrm{codim} \; f^{-1}(0)+ \dim f^{-1}(0) = \dim U
から、
\dim f^{-1}(0) + \dim f(U) = \dim U
と表現しています。また、森毅先生は、
抽象的な図をかくなら、図のようになる。よくベン図風にマルを書くが、いっそシンボル化して線にした方がはっきりする(「線型だから線にするのだ」とダジャレを言う人もある。)
とおっしゃっています。
- 佐武一郎『線型代数学』
名著と言われている本で、証明などとても詳しく、テンソルまで入っています。演習問題などもかなり深いです。
定義域を $V^n$ として、含まれる部分空間$f^{-1}(0)$の基底を延長して $V^n$の基底を作成します。延長した側(行空間側)の基底 ($n - \dim f^{-1}(0)$本)の写像が $F(V^n)$を張ること、かつそれらが一次独立になること、すなわち $f(V^n)$の基底にもなっていることを示して、
\dim f(V^n) = n - \dim f^{-1}(0) \tag{1}
を導いています。さらに、$V^n$の任意部分空間 $W$ とその直交補空間$W^{\perp}$について、
\dim W^{\perp} = n - \dim W \tag{2}
が成り立つことと組み合わせて、行ランクと列ランクが等しいこと、すなわち、
\mathrm{rank}(A^T) = \mathrm{rank}(A) \tag{3}
を導きます。その後で、(1), (2), (3) はそのうちどれか2つが分かればもう一つが導かれることを注記しています。この教科書では、行基本変形についてはほとんど扱っておらず、行列式にかなりのボリュームを割いていることもあり、行列式の言葉でもランクが定義されています。
$\mathrm{rank}(A)$ を $A$ に含まれる$\neq 0$なる小行列式の最大次数として定義することができる。
- 齋藤正彦『線形代数学』
初学者にもっともおすすめの本です(Strang 先生の本の次に)。行列の行基本変形、そしてブロック化された行列の計算を使った証明を基本に展開します。
当該の部分は、佐武の前半と全く同じ理論展開です。行ランクと列ランクが等しいことは、行列の基本変形によって本の前半で示されます。
- 松谷茂樹『線型代数学周遊』
最近購入した良書です。応用方面と数学的な進展の両方が読め、代数学者のエピソードなども豊富な面白い本です。
直接的には触れられていませんが、付録B.2 に同値類があり、商空間と零空間の解説から、当該の定理が分かります。
以下の3つの命題を同値としています。
$f: V \to W, \dim V =n, \dim W = m$ とし、
(1). $f$ の階数が r
(2). $V$の基底 $x_1,...,x_n$と $W$の基底 $y_1,...,y_m$ で以下を満たすものが存在する。
f(x_i) =
\begin{cases}
y_i & (1 \leq x \leq r)\\
0 & (r \lt x \leq n )
\end{cases}
(3). $V$の基底と$W$の基底で、それらに関する $f$ の行列表示が左上に$r$次単位行列があり、その他のブロックが零行列であるようなものが存在する。
その上で、系として、この当該定理を(1),(2)の帰結として示しています。(1)⇨(2)は佐武同様の底の延長による説明です。
\dim V = \dim Ker(f) + \mathrm{rank} \; f
- 岩堀長慶『線形代数学』
私が大学一年生で習った線形代数の教科書です(ほとんど理解できていなかったことが、Strang先生の講義を受けて分りました)。
当該の式は、数ベクトル空間については、行列 $A$ の基本変形によって証明し、線型写像としては、行列で表現して前の議論に帰着させるとともに、線形空間での佐武同様の証明も別章で加えています。
ただし後者の証明の方向は逆で、零空間の底の延長での定義域を構成からスタートするのではなく、零空間と列空間にそれぞれ基底をとり、列空間の逆像と零空間の基底を合わせて定義域の基底が作れることを示します。
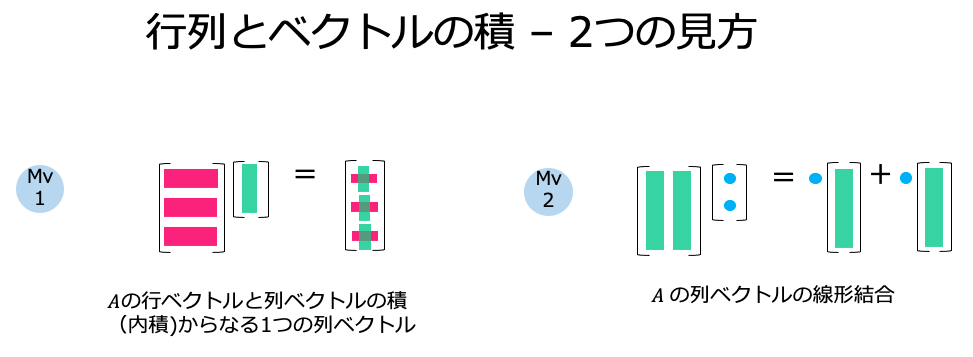
行列の掛け算を可視化
このページで出てきた行列とベクトル、行列同士の掛け算の視覚化です。左(Mv1)が零空間$N(A)$の見方で、$Ax=0$が$A$の行ベクトルと$x$が直交していることを示します。
右(Mv2)が列空間$C(A)$の見方で、$Ax$がAの列ベクトルの線型結合となることを示します。
Gilbert先生は具体的な数字による解説と、「目の慣れ」を重視して講義を進めています。こんな可視化に興味がある方は、こちらにまとまった資料
Gilbert先生は $A$ の分解を「目の慣れ」を重視して講義を進めています。こんな可視化に興味がある方は、こちらにまとまった資料
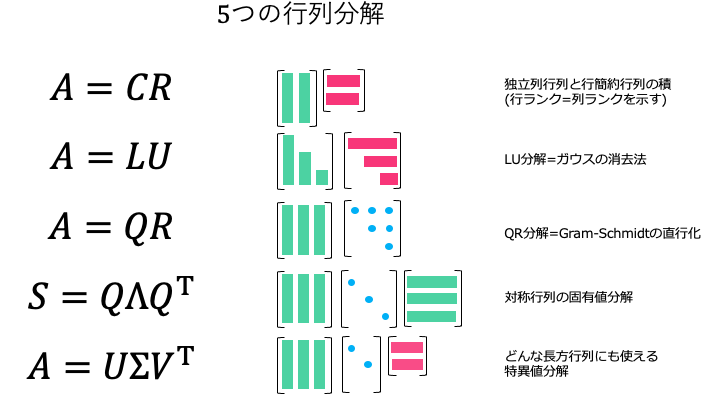
があります。今後お話する 5つの行列分解については、こんな感じです。
参考文献
数学で他に基本定理と呼ばれるもの
その他、「〜学の基本定理」(The fundamental theory)と名前がつくものには(Wikipedia)、
などの大定理があります。この定理はそれらに比べると知名度も低いですが、先生の線形代数の教育方法の1つのランドマークと言えるでしょう。
ちなみに、Steven Roman 先生は、Advanced Linear Algebra の中で「線形代数学の基本定理」を、
線形変換は始域の基底の像を決めてやれば、すべての元の行き先がもれなく決まる(変換が決まる)。また、それらの行き先は自由に決めることができる。
としています。
内省
先生の講義や本では、定理と証明を並べて行くスタイルではなく、具体的な数字と行列の形による直感的理解を重視しています。そのためか、集合論的書き方を避け、平易な英語で、記号もフランス的ではなく米国的です(転置 $A^T$ や $C(A)$)。この記事では、慣れもあって、部分空間の記述に集合的表記を使ってしまいました。日本の大学1年生を考えるとむしろこの方がすっきりするか、と思いましたが、先生はお気に召さないでしょう。さらに、行ベクトルと $x$ の内積、という書き方をしていますが、本当は双対空間の話をしないといけないのかもしれません。しかし、データが縦横に大量に並んだ行列を扱うときは、数学科的記述よりも、工学部的に直感が効く記述を好んでしているのが先生の特徴です(おかげで私は理解が突然飛躍的に進みました)。
このシリーズについて
このシリーズでは、Gilbert Strang 先生の Linear Algebra Vision 2020 を元に、この後、$CR$分解だけでなく、$LU$分解, $QR$分解(Gram-Schmidt), 固有値分解, 特異値分解(SVD) を扱っていきます。
Gilbert Strang 先生は MIT の有名な(名物)線形代数の先生です。OpenCourseware で無償で先生の講義をみることができます。
- 『線形代数イントロダクション』
- 『ストラング:教養の線形代数』(2023年新刊)
という日本語の著書があります。
今後、シリーズ化して先生の講義から目から鱗の話題を解説する予定です。
先生については、別のページで紹介します(日本語版は別途用意中)。