これは何?
- Gilbert Strang 先生から学んだ線形代数シリーズ、第一回目の記事です。シリーズ全体はこちら。
今回は、「行列の行ランクと列ランクはなぜ等しいか」について、証明ではなく直感的に理解する方法について書いてみます。
行列のランクは、その行列を構成する線形独立な行または列ベクトルの数のことです。
- 行ランク: 線形独立な行ベクトルの数
- 列ランク: 線形独立な列ベクトルの数
実際、この2つのランクは等しいことが知られていますが、これを直感的に示しましょう。この説明を初めて Strang 先生から聞いた時、目から鱗が落ちました。他の多くの教科書にはない直感的な説明だったからです(他の教科書での証明方法については参考に後で書こうと思います)。
行列の行ランクと列ランクはなぜ等しいか
$CR$分解(後述)を用いて、「行ランクと列ランクが等しい理由」を解説します。
A = \begin{bmatrix}
2 & 2 & 4 \\
4 & 4 & 8 \\
1 & 2 & 3 \\
\end{bmatrix}
列ランクは2
こんな行列があったとき、次のような手順で行列を分解します。まず、列について左から順に1列ずつ見ていきます。そして、線形独立なのものを残し、列を集めていきます。1列目、2列目と見ていって、これまで出てきたものの線型結合で表現できるもの(線形従属なもの)があれば、それは、省いて集めます。省いたものは、他の列の線形結合で表現します(この手順でできた列ベクトルの基底を「ゴーシュ基底」と呼ぶことが提案されています。ゴーシュはフランス語で左を意味します)。
この例だと、1列目と2列目は「目の子」で線形独立なので残します。3列目はどうでしょう? 同様に目の子で、
- 3列目 = 1列目 + 2列目
となっていることが分かります。ですので、3列目は、1,2列目の線形結合です。これを行列分解の形で表してみましょう。
\begin{bmatrix}
2 & 2 & 4 \\
4 & 4 & 8 \\
1 & 2 & 3 \\
\end{bmatrix}
= \begin{bmatrix}
2 & 2 \\
4 & 4 \\
1 & 2 \\
\end{bmatrix} \begin{bmatrix}
1 & 0 & ?\\
0 & 1 & ?\\
\end{bmatrix}
と書けるのがわかりますか?1列目と2列目を基底としてみて、それぞれを$(1,0), (0,1)$と表現できます。そして、3列目は、$(1,1)$と表現できるので、
\begin{eqnarray}
\begin{bmatrix} 2\\ 4\\ 1\\ \end{bmatrix} =
(1)\begin{bmatrix} 2 \\ 4 \\ 1 \\ \end{bmatrix}
+ (0) \begin{bmatrix} 2 \\ 4 \\ 2 \end{bmatrix} \\
\begin{bmatrix} 2\\ 4\\ 2\\ \end{bmatrix} =
(0)\begin{bmatrix} 2 \\ 4 \\ 1\\ \end{bmatrix}
+ (1) \begin{bmatrix} 2 \\ 4 \\ 2 \end{bmatrix} \\
\begin{bmatrix} 4\\ 8\\ 3\\ \end{bmatrix} =
(1)\begin{bmatrix} 2 \\ 4 \\ 1\\ \end{bmatrix}
+ (1) \begin{bmatrix} 2 \\ 4 \\ 2 \end{bmatrix}
\end{eqnarray}
となるのが分かりますか?こんな風に目がなれるといいでしょう。
よって、これをまとめて書くと、
\begin{bmatrix}
2 & 2 & 4 \\
4 & 4 & 8 \\
1 & 2 & 3 \\
\end{bmatrix}
= \begin{bmatrix}
2 & 2 \\
4 & 4 \\
1 & 2 \\
\end{bmatrix} \begin{bmatrix}
1 & 0 & 1\\
0 & 1 & 1\\
\end{bmatrix} \\
すなわち、
A = CR
となります。$C$ が独立な列のセット、$R$ がそれに掛かる係数です。記号的に書くと、
A = \begin{bmatrix}
| & | & | \\
a_1 & a_2 & a_3 \\
| & | & |
\end{bmatrix}
として、
\begin{eqnarray}
a_1 = (1)a_1 + (0)a_2 \\
a_2 = (0)a_1 + (1)a_2 \\
a_3 = (1)a_1 + (1)a_2 \\
\end{eqnarray}
A = \begin{bmatrix}
| & | & | \\
a_1 & a_2 & a_3 \\
| & | & |
\end{bmatrix}
= \begin{bmatrix}
| & | \\
a_1 & a_2 \\
| & |
\end{bmatrix} \begin{bmatrix}
1 & 0 & 1\\
0 & 1 & 1\\
\end{bmatrix} = CR
ここまでの手順で、列ランクは2ということが分かります。この過程で2つの線形独立な列ベクトルが得られたのですから。
行ランクも2
元の式に戻って、
A =\begin{bmatrix}
2 & 2 & 4 \\
4 & 4 & 8 \\
1 & 2 & 3 \\
\end{bmatrix}
= \begin{bmatrix}
2 & 2 \\
4 & 4 \\
1 & 2 \\
\end{bmatrix} \begin{bmatrix}
1 & 0 & 1\\
0 & 1 & 1\\
\end{bmatrix} = CR
この式を別の見方で見てみます。今度は、 $A$ の行ベクトルに注目。
A = \begin{bmatrix}
- a^*_1 - \\ - a^*_2 -\\ - a^*_3 -
\end{bmatrix}
として、
\begin{eqnarray}
a^*_1 = \begin{bmatrix} 2 & 2 & 4 \end{bmatrix} =
(2)\begin{bmatrix} 1 & 0 & 1 \\ \end{bmatrix}
+ (2) \begin{bmatrix} 0 & 1 & 1 \end{bmatrix} \\
a^*_2 = \begin{bmatrix} 4 & 4 & 8 \end{bmatrix} =
(4)\begin{bmatrix} 1 & 0 & 1 \end{bmatrix}
+ (4) \begin{bmatrix} 0 & 1 & 1 \end{bmatrix} \\
a^*_3 = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} =
(1)\begin{bmatrix} 1 & 0 & 1 \end{bmatrix}
+ (2) \begin{bmatrix} 0 & 1 & 1 \end{bmatrix}
\end{eqnarray}
すなわち、
A=CR
です。$A$ の各行は、右側に現れた $R$ 行列の各行を基底とみて、 それらの線形結合($C$が係数)で表されているのです!すなわち、行ランクも2です。
見方は、こんな感じです。
何が起こっているの?
最初は $A$ の線形独立な列を集めていました($C$) 。その数が列ランクであり、2です。全ての列ベクトルは、$C$ の2つの列ベクトルの線形結合で表現され、その係数が $R$ に現れます。
出来上がった分解をよく見ると、$A$ の各行も、2つの線形独立な行ベクトル($R$ の2つの行)の線形結合になっていて、その係数が $C$ に現れます。すなわち、行ランクも2なのです。
$C$ と $R$ はそれぞれ役割を変えて、「列ベクトルと線形結合の係数」、「線形結合の係数と行ベクトル」を表現し、それらの掛け算として $A$ が表現されるのです。
だから、「列ベクトルのランクと行ベクトルのランクは等しい」、と言うことができます。説明は以上です!
CR分解
ちなみに、この分解を「 $CR$ 分解」といいます。 $C$ は列(column)、 $R$ は行(row)を表します。そして、$R$を行簡約階段形(reduced row echelon form)といいます。おなじみ、ガウスの消去法に出てくる形で、非零要素が上からの階段になっていて、階段以下はすべて 0 。そして、ピボットの上もすべて 0 となる形です。
※ただし、普通にガウスの消去法を行うと、最下行には元の $A$ と同じ行数になるように、0ばかりからなる行が残ります。ここでの $R$ はその「0ばかりの行」を取り除いたものです。
ここから何が言える?
行列$A$の列空間を $C(A)$と書きます。ここまでの議論で、
\dim C(A) = \dim C(A^T)
が言えました( $A^T$ は Aの転置、$C(A^T)$は行空間となります)。詳しくは次回に譲りますが、このことと、行列 $A$ の零空間$ = N(A)$が行空間 $C(A^T)$と直交していること(これも次回解説)を使うと、「線形代数学の基本定理」(Wikipedia)(あるいは次元定理)が言えます。
$A \in \mathbb{ R }^{m \times n}$ とすると、
n = \dim C(A) + \dim N(A)
もしくは写像の言葉で、$A$ によって表される $ \mathbb{ R }^n $ から $ \mathbb{ R }^m $への線形写像を $f$ 、とすると、その核空間 $f^{-1}(\boldsymbol{0}) $ と値域 $f(\mathbb{ R }^n) $の次元には、
n = \dim f(\mathbb{ R }^n) + \dim f^{-1}(\boldsymbol{0})
の関係が成り立つという、線形代数の第一のハイライトです。これについては、詳しく別記事を書きました。
本が出ました(2023)
- 『ストラング:教養の線形代数』 日本語版が出ました(2023/2/11)。 表紙の $A=CR$ の意味がこの記事そのものです。

他の教科書では...
- 佐武一郎『線型代数学』
名著と言われている本で、証明などとても詳しく、テンソルまで入っています。演習問題などもかなり深いです。
この教科書では、「行列式」を重点的に先に学習するスタイルをとっています。その流れから、ランクが 「$A$ に含まれる $\ne \boldsymbol{0} $なる小行列式の最大次数である」と定義できることを利用して証明しています。
また、別の証明として、先に、前述の「線形代数学の基本定理」を証明し、「核空間」が「行空間」の「直交補空間」であることから、それ次元の和から導くこともできる、としています。
- 齋藤正彦『線形代数学』
この教科書では、行列の「右基本変形」と「左基本変形」を繰り返すことで、単位行列を左上に作成でき、他の要素をすべて 0 にできる(階数標準形)ことを使い、できた単位行列のサイズをランク $=r$ と定義しています。その上で、
- 「左基本変形」が行ベクトルの張る空間(行空間)、核(零空間)、および列ベクトルの「線形独立・従属性」を変えないこと
- 「右基本変形」が列ベクトルの張る空間(列空間・像)、および行ベクトルの「線形独立・従属性」を変えないこと
から、列ランクと行ランクがが等しいことを証明しています。
これがもっとも多くの教科書行われている一般的な証明だと思います。
行列の掛け算を可視化
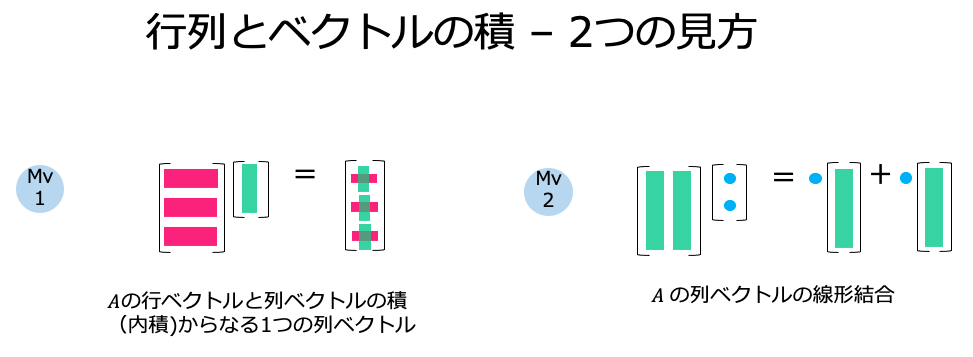
このページで出てきた行列とベクトル、行列同士の掛け算の見方に慣れない方のために、別の資料を用意しています。例えばこんな風に行列の掛け算を見れるようになるといいでしょう。左が通常の見方。今回の見方は右です。
これを使って、列はこうなります。
行も、こんな風にみてください。
線形代数に慣れてくると、目で追えるようになります。こんな可視化に興味がある方は、こちらにまとまった資料
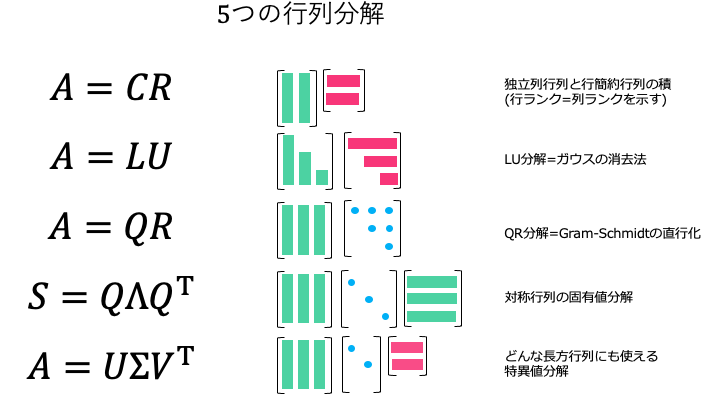
があります。今後お話する 5つの行列分解については、こんな感じです。
このシリーズについて
このシリーズでは、Gilbert Strang 先生の Linear Algebra Vision 2020 を元に、この後、$CR$分解だけでなく、$LU$分解, $QR$分解(Gram-Schmidt), 固有値分解, 特異値分解(SVD) を扱っていきます。
Gilbert Strang 先生は MIT の有名な(名物)線形代数の先生です。OpenCourseware で無償で先生の講義をみることができます。
という日本語の著書があります。
今後、シリーズ化して先生の講義から目から鱗の話題を解説する予定です。
先生については、別のページで紹介します(日本語版は別途用意中)。