例題6:端モーメントを受ける単純梁＜【② 構造力学の「構造」例題】様を参考にsympyで実行した。

Last updated at 2025-01-20Posted at 2025-01-16

前　例題5:等分布荷重を受ける両端固定梁へ
次　例題7:x=aで集中荷重を受ける片持ち梁へ
　　私のsympyの目次へ

オリジナル

Youtube 仮想仕事の原理の教育に関する研究会様　
例題6:端モーメントを受ける単純梁 (14:10〜16:00)
https://youtu.be/NMP0Q78Wl9Q?t=850
＜目次(18:50)
https://youtu.be/NMP0Q78Wl9Q?t=1130
＜フル【② 構造力学の「構造」例題】(0:00〜19:21)
https://youtu.be/NMP0Q78Wl9Q

sympyで

・ver0.2 未差し替え
・ver0.1

# ver0.1
# 例題6:端モーメントを受ける単純梁【② 構造力学の「構造」例題】を参考にsympyで実行した。
from sympy import *
var('x,C1,C2,C3,C4,Mbar,L,EI')
def myMujigennka(v,com):
    return ( str(com)+"*("
            +str((v/com).expand())                \
                 .replace("x**2/L**2","(x/L)**2") \
                 .replace("x**3/L**3","(x/L)**3") \
                 .replace("x**4/L**4","(x/L)**4") 
            +")").replace(" ","")
def myKakeruPw(v,Pw):
    return Pw+"*"+str(v).replace("*"+Pw,"")
EIv4=0                                     #;print(EIv4)
EIv3=integrate(EIv4,x)+     C1             #;print(EIv3)
EIv2=integrate(EIv3,x)+L   *C2             #;print(EIv2)
EIv1=integrate(EIv2,x)+L**2*C3             #;print(EIv1)
EIv =integrate(EIv1,x)+L**3*C4             #;print(EIv )
sol =solve([Eq(1/EI*EIv .subs({x:0}),0),   # 幾何的境界条件
            Eq(1/EI*EIv .subs({x:L}),0),
            Eq(    -EIv2.subs({x:0}),Mbar),# 力学的境界条件
            Eq(    -EIv2.subs({x:L}),0),           
           ],[C1,C2,C3,C4])                # ;print(sol)
v   =(1/EI*(EIv.subs({C1:sol[C1],C2:sol[C2],C3:sol[C3],C4:sol[C4]}))).factor()     #;print(w)
print("#",myKakeruPw(myMujigennka(v,Mbar*L**2/(6*EI)),"Mbar"))                   
print("# あと少し",                 v.subs({x:Rational(1,3)*L}))    # L*1/3に同じ
print("# あと少し",                 v.subs({x:Rational(2,3)*L}))    # L*2/3に同じ
# Mbar*L**2/(6*EI)*(2*x/L-3*(x/L)**2+(x/L)**3)
# あと少し Mbar*5*L**2/(81*EI)
# あと少し Mbar*4*L**2/(81*EI)
# 
rep={Mbar:1,L:1,EI:1}
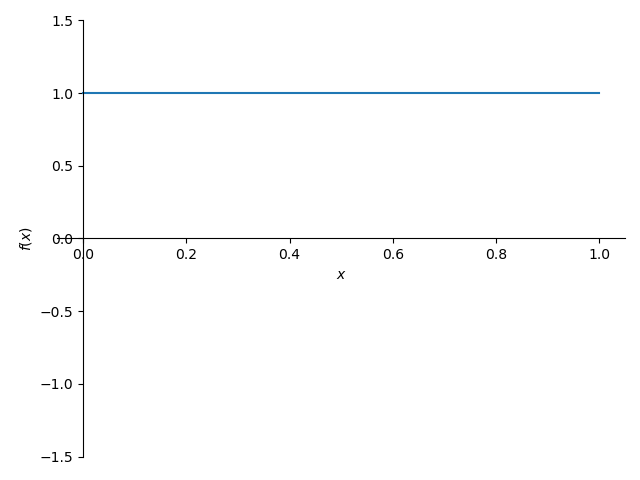
plot (diff(v,x,3).subs(rep),(x,0,1),ylim=(-1.5,1.5))
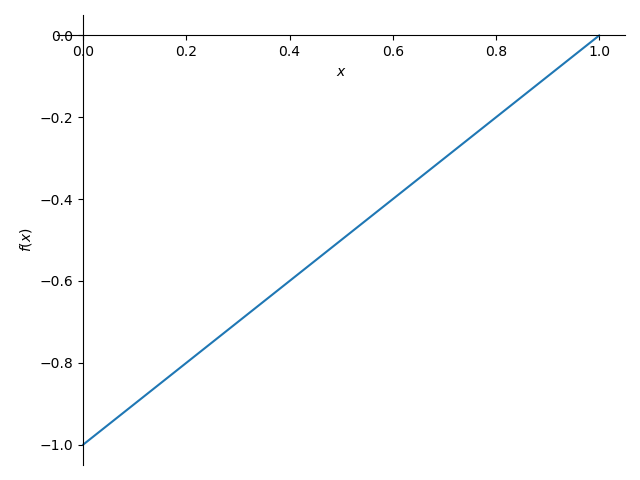
plot (diff(v,x,2).subs(rep),(x,0,1))