$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
はじめに
本記事では、IBM Quantum Challenge Fall 2022で出題された問題を復習も兼ねて記事にしたいと思います。具体的な問題は、IBM Quantum Challenge Fall 2022 Lab3で出題された「Quantum Optimization Challenge - 宇宙船を脱出させよう!」です。やっていることとしては、「TSP専用のPQCの実装とVQEによる経路最適化」です。
終了した過去のIBM Quantum Challengeの内容については、共有の制限が特に設けられていないため、本記事で共有させていただいています。今後何かルール変更が行われた場合は、速やかに準拠させていただきます。
また、私自身が量子コンピュータの学習歴が短い素人のため、間違っている点やよろしくない表現がありましたら、ご指摘をよろしくお願いいたします。
対象者
・量子コンピュータの基本的特性である「重ね合わせ」や「量子もつれ」、「測定」の概念を知っている方。
・量子コンピュータの基本的なゲート演算子は分かるものの、VQEに関しては知らない方。
・IBM Quauntum Challengeで出題される問題に興味がある方。
概要
IBM Quantum Challengeは、IBM社が主催する量子コンピュータ・プログラミングのコンテストです。IBMは量子コンピューティング用のオープンソースSDKであるQiskitを提供しており、Qiskitを利用することで、pythonによる量子コンピューティングを行うことができます。このコンテストは2019年から始まって2020年から毎年2回開催されており、ChallengeやLabと呼ばれる課題が大きく4つ出題されます。
今回のコンテストは、近未来で宇宙探索が可能になった世界において、宇宙船がブラックホールに捕まってしまったため、様々な課題(Lab1~4)をクリアして、ブラックホールの重力から抜け出そう、というテーマに沿って進められました。
中でもLab3は、以下のような文脈から巡回セールスマン問題(Traveling Salesman Problem, TSP)を量子コンピュータで解くことになっていました。
・スイングバイ航法によるブラックホールの重力影響下からの脱出を試みている
→ 対象惑星周辺のスペースデブリをドローンによって回収する必要がある
→ デブリ回収の最短経路を求める必要がある
→ 最短経路問題をTSPに落とし込み、量子コンピュータを使って解く
TSPは古典コンピュータによる求解が難しいため、量子コンピュータによる求解が期待されている問題の一つです。量子コンピュータによる求解方法の一つとして、パラメータ化された量子回路(Parameterized Quantum Circuit, PQC)のパラメータ収束によって求解する、変分量子固有値ソルバー(Variational Quantum Eigensolver, VQE)という手法があります。今回特徴的だった点は、TSPの制約条件をPQCに反映することで解の探索空間を縮小し、より高速な求解を試みるという内容でした。
なお、過去のIBM Quantum ChallengeにおけるVQE問題については、「IBM Quantum Challengeで取り扱われたVQE応用例をまとめる」の記事でまとめられているので、参考にしてください。
早速問題の解説に入っていきましょう。といきたいのですが、その前に初学者がLab3を解くにあたって必要となる知識がいくつかあります。そこで、私自身のためにもそれらについて説明した後に、Lab3に入っていこうと思います。
・もう分かっているから問題の内容を知りたい、という方は「Lab3 : TSP専用のPQCの実装とVQEによる経路最適化」
・最後の問題の答えだけ知りたい、という方は「Lab3の本題を解く」
の章まで飛ばしてください。
Lab3に必要な前提知識
Lab3では、TSPという最適化問題をVQEという量子アルゴリズムを使って解きます。さらに、TSPに特化したパラメータ化量子回路であるPQCを構築することで、より一層効率的に最適解を探索します。ここではまず、TSPとVQEについて見ていきましょう。
TSPとは
TSP(Traveling Salesman Problem, 巡回セールスマン問題)とは、各拠点と2拠点間の移動コストの集合が与えられたとき、「全ての拠点を1回ずつのみ通って出発点に戻ることのできる経路のうち、総移動コストが最小になる経路を求める」という組み合わせ最適化問題です。
TSPの定式化
IBM Quantum Challenge Fall 2022 Lab3でも説明されているように、各拠点の集合を$V$、経路順序の集合を$G$、拠点を$i$、経路順序を$p$、2拠点間の移動コストを$w_{i,j}$とすると、2値変数$x_{ip}$(バイナリ)を導入することで、TSPは2値整数計画問題として定式化することができます。2値整数計画問題の形式で定式化することで、後々量子コンピュータで求解可能な形式へと変換することができます。TSPの最小化すべき目的関数は以下で表されます。
\sum_{i,j\in V}w_{i,j}\sum_{p\in G}x_{i,p}x_{j,p+1} \tag{1}
ここで2値変数$x_{ip}$とは、$p$番目に拠点$i$を通過した場合1となり、$p$番目に拠点$i$を通過しない場合は0となる変数のことを指します。
x_{i,p}=\left\{ \tag{2}
\begin{array}{ll}
1 & (p番目に拠点iを通過する) \\
0 & (p番目に拠点iを通過しない)
\end{array}
\quad \quad \quad \quad \quad (\forall i, \ \forall p)
\right.
一方、TSPには制約条件が二つあり、1.全ての拠点が経路内で一回だけ現れる、2.各順序において必ず拠点のいずれかが出現する、という制約を満たす必要があります。これらを式で表すと以下のようになります。
制約条件1 \quad \sum_{i\in V}x_{i,p}=1 \quad \forall p \tag{3}
制約条件2 \quad \sum_{p\in G}x_{i,p}=1 \quad \forall i \tag{4}
そして、上記の目的関数と制約条件を一つの目的関数$C(X)$にまとめると、次のようになります。
C(X)=\sum_{i,j}w_{i,j}\sum_{p}x_{i,p}x_{j,p+1}+A_1\sum_{p}(1-\sum_{i}x_{i,p})^2+A_2\sum_{i}(1-\sum_{p}x_{i,p})^2 \tag{5}
第一項は目的関数であり、第二項と第三項はそれぞれ制約条件1と2をペナルティという形で表し、目的関数の中に含めています。また、$A_1$、$A_2$は各ペナルティの重みであり、値が大きいほど厳しい制約条件となります。
TSPの変換とイジングハミルトニアン
これでTSPを一つの式で定式化することができました。式(5)では、TSPという最適化問題が2次目的関数と制約関数の結合形式で表されています。このような形式の最適化問題は、QUBO(Quadratic Unconstrained Binary Optimization、二次制約なし二値最適化)と呼ばれます。
ここで、QUBOはイジングモデルのハミルトニアン(イジングハミルトニアン) に変換することができます。
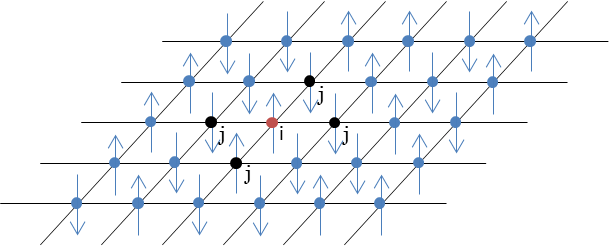
イジングモデルとは、以下のようなモデルを指します。上下を指す矢印は、QUBOの2値変数{0,1}に対応します。
イジング模型とは二つの状態をとる格子点から構成され、最隣接する格子点のみの相互作用を考えた格子模型を表しています。
難しい説明ですが、とりあえず図は以下のようになります。
ハミルトニアンとは、注目している現象(系)のエネルギーを表す行列(演算子)です。
後述のVQEといった量子アルゴリズムによって、イジングハミルトニアンの最小固有値(=QUBOの最適解)を求めることができます。
そのため、今回もTSPの最適解を求めるために、QUBOとして定式化した式(5)をイジングハミルトニアンに変換する必要があります。
では、イジングハミルトニアンはどのようにして求めるのでしょうか?
QiskitではQUBOからイジングハミルトニアンへの一連の変換をAPIを使って行うことができます。詳細な実行方法については後で説明します。
それでは次に、イジングハミルトニアンの最小固有値を求めるのに利用するVQEについて見ていきましょう。
VQEとは
VQE(Variational Quantum Eigensolver)とは、量子化学計算や組み合わせ最適化計算への応用が期待される量子アルゴリズムです。変分原理と呼ばれる原理を利用して、最小固有値問題を近似的に解き、系の安定状態や最短経路を効率的に計算することが可能です。 また、古典コンピュータと量子コンピュータの両方を使用するハイブリットな特徴を持っています。
まずはVQEの根幹である変分原理についてみていきましょう。
変分原理
こちらで紹介されているように、量子力学の世界ではハミルトニアンと呼ばれるエルミート行列$H$が与えられた場合、
H\ket{\psi} = E\ket{\psi} \tag{6}
を満たすような任意の量子状態$\ket{\psi}$とエネルギー$E$の組み合わせが存在します。式(6)は時間に依存しないシュレディンガー方程式と呼ばれます。特に、(6)式を満たすような$\ket{\psi}$は固有状態と呼ばれ、対応する$E$は固有値と呼ばれます。いわゆるハミルトニアンの固有値問題ですね。
基本的に、系はエネルギーの一番低く安定した状態(=基底状態と呼ぶ)になっています。そこで、固有状態の中でも最小固有値に対応する基底状態に注目が集まります。そして、ハミルトニアンの最小固有値と基底状態を求める際に有効な手法の一つがリッツの変分法です。変分法は以下で示される変分原理を利用して、最小固有値を求めます。
\bra{\psi}H\ket{\psi} \geq E_0 \tag{7}
これは任意の量子状態$\ket{\psi}$において、エネルギーの期待値$\bra{\psi}H\ket{\psi}$が必ず基底エネルギー(=最小固有値)$E_0$以上であることを示しています。
つまり、全ての量子状態$\ket{\psi}$を用意して、エネルギーの期待値$\bra{\psi}H\ket{\psi}$が最小の量子状態$\ket{\psi}$を見つけ出せば、基底エネルギー$E_0$と基底状態$\ket{\psi_0}$を求めることができます。実際に全ての量子状態を探索することは出来ないので、物理的・化学的経験をもとに、パラメータ化された量子状態$\ket{\psi(\theta)}$を構成し、$\bra{\psi(\theta)}H\ket{\psi(\theta)}$を最小化するような$\theta$を見つける、というアプローチがとられています。
そして、量子コンピュータを用いて、量子状態を効率的に記述できることを活用したアルゴリズムがVQEです。次に、VQEのアルゴリズムの流れを眺めながら、どの部分が量子計算化されているのかを確認しましょう。
VQEの流れ
こちらで紹介されているように、VQEの流れは以下のようになっています。
①. ハミルトニアン$H$と量子状態$\ket{\psi(\theta)}$とパラメータ初期値$\theta_0$を生成する。
②. 量子コンピュータ上で$\bra{\psi(\theta)}H\ket{\psi(\theta)}$を計算・測定し、エネルギー固有値$E$を得る。
③. 測定結果をもとに、古典コンピュータ上で$\bra{\psi(\theta)}H\ket{\psi(\theta)}$が小さくなるような$\theta$を決定する。
④. $\bra{\psi(\theta)}H\ket{\psi(\theta)}(=E_0)$が収束するまで②と③を繰り返すことで、近似的な基底状態を求める。
VOEの流れのイメージ図を以下に示します。

参考:「A variational eigenvalue solver on a photonic quantum processor」
①~④の内、手順②は量子コンピュータが威力を発揮するVQEの心臓部になります。そのため、手順②のみ詳細に説明します。
手順②
こちらで紹介されているように、量子コンピュータではユニタリ行列しか扱えないため、エルミート行列であるハミルトニアン$H$をパウリ行列$\sigma$の線形結合で表します。($a$は係数)
H=a_1\sigma_1+a_2\sigma_2+...+a_n\sigma_n \tag{8}
これは、パウリ行列$\sigma$ ($X$, $Y$, $Z$)が、エルミート行列かつユニタリ行列であるという性質を有しているため可能となっています。さらに、パウリ行列の直積は線形であるため、ハミルトニアンの固有値$E$も各ユニタリ行列の固有値の和として表現できます。
\bra{\psi(\theta)}H\ket{\psi(\theta)}=a_1\bra{\psi(\theta)}\sigma_1\ket{\psi(\theta)}+a_2\bra{\psi(\theta)}\sigma_2\ket{\psi(\theta)}+...+a_n\bra{\psi(\theta)}\sigma_n\ket{\psi(\theta)} \tag{9}
そして、この$a_k\bra{\psi(\theta)}\sigma_k\ket{\psi(\theta)}$が、図中の「Quantum module $1...N$」に相当します。各ユニタリ行列$\sigma_k$の固有値$a_k\bra{\psi(\theta)}\sigma_k\ket{\psi(\theta)}$は量子コンピュータ上の量子状態をもとに算出できます。
以上で、TSPをVQEを使って解くために必要な前提知識が揃いました。
それでは本編に入りましょう。
Lab3 : TSP専用のPQCの実装とVQEによる経路最適化
Lab3は概要でも述べた通り、ドローンによるスペースデブリ回収最短経路問題をTSPとして捉え量子計算によって求めよ、という内容でした。例えば、デブリが4つの時の各デブリとデブリ間の距離を図で表すと以下のようになります。

このくらいの最適化問題は正直古典計算のほうが早い気がしますね。。。笑
今回特徴的だったのが、TSP専用のパラメータ化された量子回路(Parameterized Quantum Circuit, PQC)を作成する誘導でした。このTSP専用のPQCでは、各制約条件を回路に反映することで解の探索空間を縮小し、VQEによる求解の高速化を図ることができます。そこでまず、TSP専用のPQCの実装について見ていきましょう。
TSP専用のPQCの実装
TSP問題に対して問題固有のPQCを実装し、探索空間を縮小して解を得る、という分野は活発に研究されています。今回の課題では、「Problem-specific parameterized quantum circuits of the VQE algorithm for optimization problems」 という論文が紹介されており、この論文中に提案されたPQCを実装します。
論文中ではTSP専用のPQCの実装方法を段階的に示しており、Lab3もこの流れに沿っています。
具体的には3段階あり、
- 制約条件1のみを満たすPQCの実装 (The first case)
- 制約条件1および制約条件2の一部($i=1$のみ)を満たすPQCの実装 (The second/Third case)
-
全ての制約条件を満たすPQCの実装 (The fourth case)
という流れです。以下に概念図を示します。ここでは、拠点を$i$、順序を$p$としています。

参考:「Problem-specific parameterized quantum circuits of the VQE algorithm for optimization problems」
図中の2値変数$x_{i,p}$の正方行列では、各行は各順序$p$においてどの拠点を通過するのかを表し、各列は各拠点$i$がどの順序において通過するかを表しています。ただし、通過する$x$のみ1でそれ以外は0です。この図は後々出てくるので、頭の片隅にいれておく程度でよいです。
それでは、実際に問題を解いてみましょう。
Qiskitの各種ライブラリ
必要となるQiskitの各種ライブラリを示します。
from qiskit_ibm_runtime import QiskitRuntimeService, Session, Estimator, Sampler, Options
from qiskit.circuit import ParameterVector, QuantumCircuit
from qiskit_aer import Aer
from qiskit.algorithms import MinimumEigensolver, NumPyMinimumEigensolver, VQE
from qiskit.algorithms.optimizers import SPSA
from qiskit.utils import algorithm_globals
from qiskit_optimization.algorithms import MinimumEigenOptimizer
from qiskit_optimization.applications import Tsp
from qiskit_optimization.problems import QuadraticProgram
from qiskit_optimization.converters import QuadraticProgramToQubo
制約条件1のみを満たすPQC
まず、TSPの制約条件1のみを満たすPQCを実装します。
制約条件1は、それぞれの順序$p$において1拠点だけに訪問できるという制約で、以下の式で表されます。
\sum_{i\in V}x_{i,p}=1 \quad \forall p
この制約の特徴は、各制約において2値変数$x_{i,p}$が1つのみ1で、それ以外はすべて0であることです。この制約に対応して、解の集合は$W$状態に対応する基底の集合$\ket{\psi_{i}}$に制限されます。$W$状態とは、量子ビットのうち1つのみが$\ket1$で、それ以外の全ての量子ビットが$\ket{0}$である状態の重ね合わせです。 具体的には以下の式で表されます。
\ket{W(\phi)}=\sum_{i}{\alpha_{i(\phi)}\ket{\psi_{i}}} \tag{10}
\sum_{i}{|\alpha_{i(\phi)}|^2}=1
\ket{\psi_{i}}\in \{\ket{100...0},\ket{010...0},...,\ket{000...1}\}
ここで、解の集合が$W$状態に対応する基底の集合に制限されるとはどういうことでしょうか。
$n$量子ビットで表される解を$\ket{\psi_{\alpha}}$とすると、$\ket{\psi_{\alpha}}$は本来、
\ket{\psi_{\alpha}}\in \{\ket{100...0},\ket{110...0},...,\ket{101...0},...,\ket{111...1}\}
という基底の集合に属します。そのため、解$\ket{\psi_{\alpha}}$の場合の数は$2^n$になります。しかし、制約条件1を考慮すると、$\ket{\psi_{\alpha}}$は$W$状態の基底のいずれかになるため、場合の数は$n$までに縮小するということです。そして、各順序における解の重ね合わせ状態は、$W$状態に対応する基底集合の線形結合で表すことができます。TSPでは制約条件1を各順序において満たす必要があるため、拠点$N$における解の場合の数は、$2^N \times N$から、$N^2$まで縮小することになります。 このように、制約条件を量子回路に反映させることで、探索する解空間を縮小させることができます。これによって、より早い解の収束が可能になるのです。
W状態を量子回路で生成する関数
$n$量子ビットにおける$W$状態を表すPQCの実装手順は、次のようになります。なお、初期状態はすべて$\ket{0}$であるとします。
- $1$番目の量子ビットに$X_{1}$ゲートを適用して$\ket{1}$とする。
- $i+1$番目の量子ビットに$R_{y_{i+1}}(\theta_{i})$ゲートを適用する。
- $i+1$番目の量子ビットに$CZ_{i,\ i+1}$ゲートを適用する。
- $i+1$番目の量子ビットに$R_{y_{i+1}}(-\theta_{i})$ゲートを適用する。
- 手順2~4の操作を$i=1,2,...,n-1$の範囲で繰り返す。
- 最後に、$CX_{j+1,\ j}$ゲートの適用を$j=1,2,...,n-1$の範囲で繰り返す。
例えば3量子ビットでは、以下の図のような回路になります。

参考:「Problem-specific parameterized quantum circuits of the VQE algorithm for optimization problems」
TSPの場合、拠点数が$N$だとすると、拠点数と順序の全組み合わせ数である$N^2$量子ビットが必要になります。また、制約条件1は、各順序において満たす必要があるため、$N$量子ビットごとに制約がかけられることになります。そのため、上記の操作を$N$量子ビットごとに合計$N$回行うことで、順序$p$ごとの量子ビット$q_{p,1}$~$q_{p,N}$で表される$W$状態を重ね合わせた状態を表すPQCを構築することができます。このPQCのイメージを以下の左図に示します。また、右図はTSPの2値変数$x_{i,p}$の正方行列であり、水色の線で囲まれた範囲は、各順序$p$における制約条件1の適用範囲を示しています。左右の図を比べることで、2値変数$x_{i,p}$と量子ビット$q_{p,i}$の対応関係を把握することができると思います。制約条件の適用範囲は、2値変数正方行列で考えることで理解しやすい一方、実際には量子回路に反映させる必要があるため、2値変数と量子ビットの対応関係を把握することは重要です。

参考:「Problem-specific parameterized quantum circuits of the VQE algorithm for optimization problems」
量子ビット$q_{p,i}$と前述した2値変数$x_{i,p}$は、拠点$i$と順序$p$の順番が入れ替わっていることに注意してください。具体的な例として、拠点数$N=3$の場合におけるPQCを以下に示します。

3量子ビットに作用する$W$状態の重ね合わせ回路が$3$回繰り返されているのが分かりますね。手順を繰り返す際には、各ゲートを適用する量子ビット番号に気を付ける必要があります。実際に作成した関数は以下のようになります。今回はゲートを適用する周期性を変数$a$、$b$で表しています。
# Nは拠点数
def tsp_entangler(N):
# 量子回路とパラメータθの設定
circuit = QuantumCircuit(N**2)
theta = ParameterVector('theta',length=(N-1)*N)
for k in range(N):
circuit.x(k*N) #手順1
for k in range(N):
a = k*N
b = k*(N-1)
for i in range(N-1): #手順5
circuit.ry(theta[i+b],i+1+a) #手順2
circuit.cz(i+a,i+1+a) #手順3
circuit.ry(-theta[i+b],i+1+a) #手順4
for i in range(N-1):
circuit.cx(i+1+a, i+a) #手順6
return circuit
$N=3$の場合は、次のようにして回路を構築します。
PQC = tsp_entangler(3)
tsp_entangler関数によって、初期状態から$W$状態に変換する回路を構築することができました。
VQE関数の作成
次に、作成した回路にパラメータ初期値を設定し、VQEを実行することで、最適化時のパラメータを求めていきましょう。
VQEを実行するためのVQE関数は以下のようになります。
def RunVQE(estimator, model, optimizer, operator, init=None):
# 一時的な解を保存
history = {"eval_count": [], "parameters": [], "mean": [], "metadata": []}
def store_intermediate_result(eval_count, parameters, mean, metadata):
history["eval_count"].append(eval_count)
history["parameters"].append(parameters)
history["mean"].append(mean.real)
# VQE実行オブジェクトの作成
vqe = VQE(estimator=estimator, ansatz=model, optimizer=optimizer, initial_point=init)
# VQEによる最小固有値の求解
result = vqe.compute_minimum_eigenvalue(operator=operator)
return result, history["mean"]
RunVQE関数の引数を見ていきましょう。modelはtsp_entangler関数によって作成されるPQCです。optimizerはパラメータ$\theta$を収束させる古典的アルゴリズムです。operatorはTSPのイジングハミルトニアン$H$のゲート演算子です。initはパラメータの初期値です。ここで重要なことは、解の重ね合わせを表すPQC(model)に対して、ハミルトニアン$H$のゲート演算子(operator)を作用させているということです。
では、$N=3$の場合のVQE実行の結果を見てみましょう。
# ランダムシードの指定
algorithm_globals.random_seed = 123
# パラメータ収束のための古典的アルゴリズムの指定(Classical Optimizer)
optimizer = SPSA(maxiter=50)
#初期パラメータの指定
np.random.seed(10)
init = np.random.rand((n-1)*n) * 2 * np.pi
#量子デバイスの指定
backend = service.backends(simulator=True)[0]
#estimatorオブジェクトの作成
estimator = Estimator()
#ゲート(演算子)の指定(=TSPから変換したハミルトニアン)
operator = qubitOp
# VQEの実行
with Session(service = service, backend = backend):
result, mean = RunVQE(estimator, PQC, optimizer, operator, init)
# VQEの実行結果を表示
print(result)
{ 'aux_operators_evaluated': None,
'cost_function_evals': 100,
'eigenvalue': -4750.85369976058,
'optimal_circuit': <qiskit.circuit.quantumcircuit.QuantumCircuit object at 0x7f54fc1b47f0>,
'optimal_parameters': { ParameterVectorElement(theta[4]): 4.706895428144666,
ParameterVectorElement(theta[3]): 4.70869194010299,
ParameterVectorElement(theta[5]): 3.147716694624536,
ParameterVectorElement(theta[2]): 4.708620211338824,
ParameterVectorElement(theta[1]): -1.660067101003188,
ParameterVectorElement(theta[0]): 3.1405938762891474},
'optimal_point': array([ 3.14059388, -1.6600671 , 4.70862021, 4.70869194, 4.70689543,
3.14771669]),
'optimal_value': -4750.85369976058,
'optimizer_evals': None,
'optimizer_result': <qiskit.algorithms.optimizers.optimizer.OptimizerResult object at 0x7f550dcffdc0>,
'optimizer_time': 1.2629129886627197}
CPU times: user 1.02 s, sys: 37.5 ms, total: 1.06 s
Wall time: 1.27 s
VQEの実行結果として、最適化された固有値がeigenvalueに、最適化パラメータ$\theta$がoptimal_parametersに格納されていることが分かります。また、最適化パラメータ$\theta$によって最適化されたPQCがoptimal_circuitに格納されています。このように、最適化されたパラメータ$\theta$を得ることができました。
固有状態の計算
最後に、VQEによって収束した最適なパラメータ$\theta$から構成されたPQCを測定することで、最小固有値に対応する固有状態を求めます。ただし、固有状態は量子的に重ね合わせた状態になっており、測定によって一意の状態に定まります。そのため、一回の測定結果からでは最適な固有状態を得たとは言い難く、測定を重ねて作成した固有状態の疑似確率分布から、最適解を得る必要があります。 Qiskitでは、Samplerと呼ばれる測定サンプリングAPIがあるため、今回はこちらを利用します。
Samplerを使用して、固有状態の最適解を計算する関数は、以下のようになります。
def BestBitstring(result, optimal_circuit):
# 系のエネルギーの取得
energy = result.eigenvalue.real
# シミュレーションのオプション設定
options = Options(simulator={"seed_simulator": 42},resilience_level=0)
# 量子デバイスとのSessionを確立
with Session(service = service, backend = backend):
# Samplerオブジェクトの生成
sampler = Sampler(options=options)
# サンプリングの実行
# VQEによる最適な回路と最適なパラメータを使って、shotsの回数だけサンプリングを実行
job = sampler.run(circuits=optimal_circuit, parameter_values=list(result.optimal_parameters.values()), shots=10000)
sampler_result = job.result()
# 固有状態の疑似確率分布を、真の確率分布に変換
result_prob_dist = qiskit.result.QuasiDistribution.nearest_probability_distribution(sampler_result.quasi_dists[0])
# 固有状態の確率分布から、最も確率の高い値を最適解(バイナリ形式)として取得
max_key = format(max(result_prob_dist, key = result_prob_dist.get),"016b")
#最適解を配列に格納
result_bitstring = np.array(list(map(int, max_key)))
return energy, sampler_result, result_prob_dist, result_bitstring
このBestBitString関数を用いて、$N=3$の場合における最適解を求めます。
# VQEの結果から最適な量子回路を抽出
optimal = result.optimal_circuit.measure_all(inplace=False)
# 最適化計算を実行
with Session(service=service, backend=backend):
energy, sampler_result, result_prob_dist, result_bitstring = BestBitstring(result=result, optimal_circuit=optimal)
# 最適化計算の結果を出力
print("Optimal bitstring = ", result_bitstring[7:])
TSPCost(energy = energy, result_bitstring = result_bitstring[7:], adj_matrix = adj_matrix)
Optimal bitstring = [0 1 0 1 0 0 0 0 1]
-------------------
Energy: -4750.85369976058
Tsp objective: 130.14630023942027
Feasibility: True
Solution Vector: [1, 0, 2]
Solution Objective: 130.0
-------------------
TSPCost関数は、最適化計算の結果を出力するために定義した関数です。
このように、制約条件1のみを満たすPQCを構築・実行し、最適解を求めることができました。
制約条件1および制約条件2の一部(i=1のみ)を満たすPQC
次に、 制約条件1だけでなく制約条件2の一部も考慮して、探索部分空間をより縮小していきましょう。制約条件2は、それぞれの拠点$i$において経路内で1回だけ訪問できるという制約で、以下の式で表されます。
\sum_{p\in G}x_{i,p}=1 \quad \forall i
この章では、特に$i=1$の場合にのみ注目してPQCを構築します。すなわち、追加する制約条件は、
\sum_{p\in G}x_{1,p}=1 \tag{11}
となります。ここでは、以下の手順で新たな制約条件をPQCに反映していきます。
- 制約条件1の一部($p=1$)と制約条件2の一部($i=1$)を組み合わせたL字型制約条件の実装
- L字型制約を除いた部分において、制約条件1を満たすPQCの実装およびブリッジの実装
- 手順1と2の回路の合成
制約条件1の一部(p=1)と制約条件2の一部(i=1)を組み合わせたL字型制約条件の実装
制約条件1の一部($p=1$)と制約条件2の一部($i=1$)の適用範囲を示す2値変数行列の概念図(右)と、その2つの制約を組み合わせたL字型制約を満たすPQCの概念図(左)を以下に示します。$p=1$における制約条件1は、右図の水色の線で囲われた範囲の2値変数$x_{k,1}$の合計が1であることを示し、$i=1$における制約条件2は、右図の赤色の線で囲われた範囲の2値変数$x_{1,k}$の合計が1であることを示しています。 この二つを組み合わせると、右図のTSPの2値変数$x$正方行列において、'L'字型の制約になっていることが分かります。L字型制約を量子回路に反映させたイメージが左図となっています。

参考:「IBM Quantum Challenge Fall 2022 Lab3」
L字制約を反映させた量子回路の実装手順は、次のようになります。
- L字の角である$q_{1,1}$に対して、$R_{y}(\phi_{0})$ゲートを適用する。
- $q_{1,1}$と$q_{1,2}$と$CNOT$ゲートによって、垂直方向にもつれさせる。(制約条件2)
- $q_{1,1}$と$q_{2,1}$と$CNOT$ゲートによって、水平方向にもつれさせる。(制約条件1)
- $q_{1,1}$を除いた残りの垂直方向の要素$q_{1,p}$で$W$状態を構築。(制約条件2)
- $q_{1,1}$を除いた残りの水平方向の要素$q_{i,1}$で$W$状態を構築。(制約条件1)
注目すべき量子ビットは$q_{1,1}$です。 制約条件2と制約条件1を組み合わせるために、それぞれ$(q_{1,1},\ q_{1,2})$、$(q_{1,1},\ q_{2,1})$に対して$CNOT$ゲートを適用し、右図の水平方向と垂直方向のもつれ(=L字のもつれ)を実現させています。
では、$N=3$の場合を見てみましょう。
後々の制約条件の強化によって、作用させるべき量子ビットの番号は変化するため、今回はハードコーディングしています。
n = 3
l_circuit = QuantumCircuit(n**2)
theta = ParameterVector('theta',length=(n-1)*n-1)
# L字のもつれを構築 手順1,2,3
l_circuit.ry(theta[0],0)
l_circuit.cx(0,1)
l_circuit.cx(0,3)
l_circuit.barrier()
# 垂直方向(制約条件2)のW状態を作成 手順4
l_circuit.x(1)
l_circuit.ry(theta[1],2)
l_circuit.cz(1,2)
l_circuit.ry(-theta[1],2)
l_circuit.cx(2,1)
# 水平方向(制約条件1)のW状態を作成 手順5
l_circuit.x(3)
l_circuit.ry(theta[2],6)
l_circuit.cz(3,6)
l_circuit.ry(-theta[2],6)
l_circuit.cx(6,3)
l_circuit.draw("mpl")
PQCは以下のようになります。ここで、回路のゲートを区切るbarrier関数を適宜入れています。
通常回路では、各ゲートが左詰めで表記されてしまうため、各ゲートの役割が分かりにくくなってしまいます。
そこで、barrier関数を入れることによって視認性の向上を図っています。なお、回路に何かの作用を追加するものではありません。図において、灰色の縦太線と黒色の縦点線がbarrier関数です。

L字型制約を除いた部分とブリッジの実装
TSPの2値変数正方行列において、L字型制約の部分を除くと、次の右図のように再び制約条件1のみの2値変数正方行列の集合になっていることがわかります。そのため、左図では、$W(\phi_{p^{'}})$として表される「L字型制約を除いた部分」を$W$状態として実装します。また、左図では、$q_{1,\ p^{'}}$と$q_{2,\ p^{'}}$に対して$CNOT$ゲートが適用されています。これは、L字型とそれ以外の部分をつなぐブリッジであり、お互いをもつれさせることで、結びつけることができます。

参考:「IBM Quantum Challenge Fall 2022 Lab3」
次の図において、$q_{1,\ p^{'}}$と$q_{2,\ p^{'}}$に対する$CNOT$ゲートの作用が、手順aとbの回路をつなぐブリッジの役割を果たしていることが分かります。

参考:「IBM Quantum Challenge Fall 2022 Lab3」
では、$N=3$の場合における、 L字型制約を除いた部分とブリッジの実装を見ていきましょう。
# L字型制約を除いた部分の実装
## 回路の初期化
r_circuit = QuantumCircuit(n**2)
theta = ParameterVector('theta',length=(n-1)*n-1)
# p=2における制約条件1をW状態で表現
r_circuit.x(4)
r_circuit.ry(theta[3],5)
r_circuit.cz(4,5)
r_circuit.ry(-theta[3],5)
r_circuit.cx(5,4)
# p=3における制約条件1をW状態で表現
r_circuit.x(7)
r_circuit.ry(theta[4],8)
r_circuit.cz(7,8)
r_circuit.ry(-theta[4],8)
r_circuit.cx(8,7)
# ブリッジ部分の実装
## 回路の初期化
bridge_circuit = QuantumCircuit(n**2)
## ブリッジの作成
bridge_circuit.barrier()
bridge_circuit.cx(3,4)
bridge_circuit.cx(6,7)
bridge_circuit.barrier()
手順1と2の回路の合成
model_2 = QuantumCircuit(n**2)
theta = ParameterVector('theta',length=(n-1)*n-1)
model_2 = l_circuit.compose(bridge_circuit).compose(r_circuit)
model_2.draw(output="mpl", fold=1000)
回路を確認すると、以下のようになります。

このように、制約条件1と制約条件2の一部を満たすPQCを実装することができました。
全ての制約条件を満たすPQC
最後に、全ての制約条件を満たすPQCを実装していきましょう。IBM Quantum Challenge Fall 2022 Lab3でも説明されているように、全ての制約条件を考慮すると、固有状態の基底の集合には実現可能な解のみが含まれることになります。TSPにおいて全ての制約条件を考慮すると、2値変数正方行列の各行と各列に1が1つしかないことが分かります。このような行列は置換行列と呼ばれ、$n \times n$行列における置換行列の数は$n$個になります。すなわち、拠点数$N$における解の場合の数は、制約条件がない場合の$2^N$から$N$まで縮小することになります。例えば$N=2$の時は、
\begin{bmatrix}
1 & 0\\
0 & 1
\end{bmatrix}
,
\begin{bmatrix}
0 & 1\\
1 & 0
\end{bmatrix}
の2つが実現可能な解となります。このような任意の$N$に対するPQCは再帰的な方法で実装できることが分かっています。すなわち、$N=2$の回路から、$N=3, 4, ... k$の場合の回路を実装できます。$k \times k$ の置換行列を $(k-1) \times (k-1)$ の置換行列から作成する手順は次のようになります。
- $(k-1) \times (k-1)$ の置換行列に、0のみで構成される行と列を1つずつ追加
- 右上の角の値0を1に置き換える。
- 最後の列を各列と交換し、置換行列の集合を作成。
このようにして、$(k-1) \times (k-1)$ の置換行列の集合から、$k \times k$ の置換行列の集合を作成することができます。このイメージ図は以下のようになります。

参考:「Problem-specific parameterized quantum circuits of the VQE algorithm for optimization problems」
では、上記の手順を量子ビットに適用していきましょう。手順は以下のようになります。
- $2k-1$個の量子ビットを用意し、順番に$q_{k, p'},\ q_{v, k}(p'= 1 ... k-1,\ v= 1 ... k)$とラベル付けする。
この時、$k$列目に追加した量子ビットの集合は、{$q_{k, p'}|p'=1 ... k-1$}であり、$1$行目に追加した量子ビットの集合は、{$q_{v, k}|v=1 ... k$}である。 - 追加した$k-1$個の量子ビットにおける$W$状態のゲートを、$k$列目に追加した量子ビットの集合{$q_{v, k}|v=1 ... k$}に適用。
- すべての$v'=1 ... k-1$に対して{$CSWAP_{q_{v',k}、q_{k,p'}、q_{v',p'}}|p'=1 ... k-1$}を適用する。
この時、$v'$は列番号を表しており、$1$行目の各列の要素$q_{v',k}$を制御ビットとして、$k$列目かつ$p'$行目の要素$q_{k,p'}$と$v'$列目の$p'$行目の要素$q_{v',p'}$をスワップ対象とした$CSWAP$ゲートを適用するという意味になります。この手順のイメージ図は以下のようになります。

参考:「Problem-specific parameterized quantum circuits of the VQE algorithm for optimization problems」
では、$N=3$の場合を見てみましょう。$2 \times 3 -1 =5$量子ビットを追加して上記の手順を進めていきます。量子回路中の$q_2$は$q_{3,1}$を意味するので、$CNOT$ゲートの位置が変化していることに注意してください。
n = 3
model_3 = QuantumCircuit(n**2)
theta = ParameterVector('theta',length=(n-1)*n//2)
# N=2における置換行列の作成(上図の青線で囲われた箇所)
## 2量子ビット(q_0,q_1)におけるW状態の作成
model_3.x(0)
model_3.ry(theta[0],1)
model_3.cz(0,1)
model_3.ry(-theta[0],1)
model_3.cx(1,0)
model_3.barrier()
## 2×2行列の対角成分でCNOTゲートを作用させる。
model_3.cx(1,3)
model_3.cx(0,4)
model_3.barrier()
# 追加した量子ビットの行の部分をW状態にする(上図の赤線で囲われた箇所)
model_3.x(6)
model_3.ry(theta[1],7)
model_3.cz(6,7)
model_3.ry(-theta[1],7)
model_3.ry(theta[2],8)
model_3.cz(7,8)
model_3.ry(-theta[2],8)
model_3.cx(7,6)
model_3.cx(8,7)
model_3.barrier()
# (N-1)^2列分だけCSWAPさせる(上図の緑で囲われた箇所を列ごとに移動させながら、swapさせる)
model_3.cswap(6,2,0)
model_3.cswap(6,5,3)
model_3.cswap(7,2,1)
model_3.cswap(7,5,4)
model_3.draw(output="mpl", fold=300)
回路を確認すると、以下のようになります。

$3 \times 3$の置換行列の集合を量子ビットの重ね合わせ状態で表すことができました。
ここで回路の深さを見るため、barrier関数を除くと次のようになります。

depth関数を使って回路の深さを確認したところ$8$でした。
次に、VQEを実行し、得られた最適化パラメータから最適解を求めていきます。
# RunVQEに渡す引数の設定
estimator = Estimator()
optimizer = SPSA()
np.random.seed(10)
operator = qubitOp
init_3 = np.random.rand((n-1)*n//2) * 2 * np.pi
# RunVQEの呼び出し
with Session(service = service, backend = backend):
result_m3, mean_m3 = RunVQE(Estimator(), model_3, optimizer, qubitOp, init=init_3)
# VQEの結果から最適な量子回路を抽出
optimal_m3 = result_m3.optimal_circuit.measure_all(inplace=False)
# 最適化計算を実行
with Session(service=service, backend=backend):
energy_m3, sampler_result_m3, result_val_m3, result_m3_bitstring = BestBitstring(result=result_m3, optimal_circuit=optimal_m3)
# 最適化計算の結果を出力
print("Optimal bitstring = ", result_m3_bitstring[7:])
TSPCost(energy = energy_m3, result_bitstring = result_m3_bitstring[7:], adj_matrix = adj_matrix)
結果は以下のようになります。
Optimal bitstring = [0 0 1 0 1 0 1 0 0]
-------------------
Energy: -4751.000000000001
Tsp objective: 129.9999999999991
Feasibility: True
Solution Vector: [2, 1, 0]
Solution Objective: 130.0
-------------------
$N=3$における経路問題と最適化経路を図で表すと以下のようになります。

これで、拠点数$N=3$におけるTSPの最適解を求めることができました。
Lab3の本題を解く
遂に最後です。Lab3の主題である「主要な4つのデブリの座標と各デブリ間の距離が与えられたとき、TSPとしての制約条件を考慮した最短経路をVQEによって求めよ」を解いていきましょう。すなわち、$N=4$におけるTSP問題です。
置換行列を実装する一般化関数
ここがLab3における一番の山場かと思います。置換行列の集合をPQCに実装するにあたって、$N=3$では各ゲートを作用させる量子ビット番号をハードコーディングしていましたが、今回は$N \geq 4$のスケーリングも想定して、一般化関数を定義しました。なお、Lab3では、関数の一般化は求められていないので、ハードコーディングでも大丈夫です。
実装において、ゲートを作用させる量子ビットの番号は、全体の置換行列の大きさによって少し変則的に変化するので注意が必要です。$N\times N$の置換行列を作成する関数は以下のようになります。なお適宜barrier関数を挟んでいます。
def tsp_permutation(n, model, theta):
# nは拠点数
# 2×2の置換行列の作成
def create_permutation(model):
## W状態の作成
model.x(0)
model.ry(theta[0],1)
model.cz(0,1)
model.ry(-theta[0],1)
model.cx(1,0)
model.barrier()
## 対角成分でCNOTゲートを作用
model.cx(1,n)
model.cx(0,n+1)
model.barrier()
return model
# N×Nの置換行列の作成(N>2)
def expand_permutation(N, model, theta):
a = n*(N-1)
k = 0
for i in range(2, N+1):
k += i-2
## W状態の作成
model.x(a)
for i in range(N-1):
model.ry(theta[i+k],i+a+1)
model.cz(i+a,i+a+1)
model.ry(-theta[i+k],i+a+1)
for i in range(N-1):
model.cx(i+a+1,i+a)
model.barrier()
## SWAPゲートを作用
for i in range(N-1):
for j in range(N-1):
model.cswap(i+a,(N-1)+n*j,i+n*j)
model.barrier()
return model
if n >= 3:
model = create_permutation(model)
for i in range(3, n+1):
model = expand_permutation(i, model, theta)
elif n >= 2:
model = create_permutation(model)
else:
print("Invalid value")
return model
では、tsp_permutation関数を使って$N=4$におけるPQCを確認してみましょう。
# 拠点数と必要な量子ビット数
n = 4
num_qubits = n**2
# TSPの制約条件を反映したPQCの実装
model = QuantumCircuit(num_qubits)
theta = ParameterVector('theta',length=(n-1)*n//2)
PQC_model = tsp_permutation(n, model, theta)
PQC_model.draw(fold=1000)

$3 \times 3$の置換行列の集合から$4 \times 4$の置換行列の集合を作成する手順通りに、回路が構成されていることが分かります。
barrier関数を除いた場合のPQCは以下のようになります。

回路の深さは$11$でした。
一応$N=5$のときのPQCも確認してみましょう。
# 拠点数と必要な量子ビット数
n = 5
num_qubits = n**2
# TSPの制約条件を反映したPQCの実装
model = QuantumCircuit(num_qubits)
theta = ParameterVector('theta',length=(n-1)*n//2)
PQC_model = tsp_permutation(n, model, theta)
PQC_model.draw(fold=1000)
barrier関数あり

barrier関数なし

回路の深さは$14$でした。$N=3,4,5$の場合から、回路の深さ$d$と拠点数$N$には、$d=3N-1 \ (N \geq2)$という関係が成り立ちそうなことが分かります。
主要な4つのデブリを回収する最短経路を求める
拠点数$N=4$の置換行列を反映したPQCに、TSPのイジングハミルトニアンを適用して、VQEによる最小固有値の求解を行いましょう。
# 拠点数と必要な量子ビット数
n = 4
num_qubits = n**2
# TSPの制約条件を反映したPQCの実装
model = QuantumCircuit(num_qubits)
theta = ParameterVector('theta',length=(n-1)*n//2)
PQC_model = tsp_permutation(n, model, theta)
# tsp問題の取得
tsp = Tsp.create_random_instance(n, seed=123)
# tspのQUBO形式からイジングハミルトニアンへの変換
qp = tsp.to_quadratic_program()
qp2qubo = QuadraticProgramToQubo()
qubo = qp2qubo.convert(qp)
qubitOp_4, _ = qubo.to_ising()
# 各種設定
algorithm_globals.random_seed = 1024
optimizer = SPSA(maxiter=100)
np.random.seed(10)
init = np.random.rand((n-1)*n//2) * 2 * np.pi
backend = service.backends(simulator=True)[0]
# VQEの実行
with Session(service = service, backend = backend):
result_4, mean = RunVQE(Estimator(), PQC_model, optimizer, qubitOp_4, init=init)
# 最適化回路の抽出
optimal = result_4.optimal_circuit.measure_all(inplace=False)
# 最適化計算の実行
with Session(service=service, backend=backend):
energy, sampler_result, result_val, bitstring = BestBitstring(result=result_4, optimal_circuit=optimal)
# 最適化計算の結果を出力
print("Optimal bitstring = ", bitstring[7:])
TSPCost(energy = energy, result_bitstring = bitstring[7:], adj_matrix = adj_matrix)
結果は以下のようになります。
Optimal bitstring = [0 1 0 0 0 0 0 1 1 0 0 0 0 0 1 0]
-------------------
Energy: -51520.0
Tsp objective: 236.0
Feasibility: True
Solution Vector: [1, 2, 3, 0]
Solution Objective: 236.0
-------------------
$N=4$における経路問題と最適化経路を図で表すと以下のようになります。

見事主要な4つのデブリを回収する最短経路を求めることができました。
振り返ってみると、VQEはQiskitのAPIを使えば簡単に実行できることが分かりました。一方で、解の探索空間を縮小するための、TSPの制約条件を回路に反映する実装は、初学者の私にとってはなかなか大変でした。また本来は、従来の手法とVQEとの比較として、解の収束スピードや計算精度などについて考える必要があるのですが、今回は割愛させていただきます。
最後に
ご質問やご指摘等ありましたらコメントまでお願い致します。
参考文献
・IBM Quantum Challenge Fall 2022 Lab3
・IBM Quantum Challengeで取り扱われたVQE応用例をまとめる
・Fixstars Amplify SDKで、東京観光の最適巡回ルートを求めてみた!
・イジングモデル (Ising model)
・5-1. Variational Quantum Eigensolver(VQE)アルゴリズム
・VQEについて調べてみた
・A variational eigenvalue solver on a quantum processor
・Problem-specific Parameterized Quantum Circuits of the VQE Algorithm for Optimization Problems