Fixstars Amplify SDKで、東京観光の最適巡回ルートを求めてみた！

はじめに

こんにちは！
本記事では、Fixstars社から提供されているイジングマシン（量子アニーリングマシンを含む）向けライブラリであるFixstars Amplify SDKを紹介し、その後、Amplifyを使って、組み合わせ最適化問題を解いていきたいと思います。具体的には、このサイトを参考にして、さまざまな制約下での、東京スカイツリーの撮影スポットの最適巡回ルートの求解を行いたいと思います。

量子アニーリングに関しては、まだまだ勉強中のため、間違っている点もあるかもしれませんが、その際は、有識者の皆様方、（優しく）ご指摘をお願いしますm(__)m

本記事で書くこと

• Fixstars Amplify SDKについての説明。
• 利用にあたって、必要なイジングマシンやその入力形式（QUBOやイジング模型）の説明。
• Fixstars Amplify SDKを用いた、東京スカイツリーの撮影スポットの最適巡回ルートの求解。
  • 参考：【保存版】東京スカイツリーのおすすめ撮影スポットまとめ

本記事の対象者

• 量子アニーリング技術に興味がある方。
• 組み合わせ最適化については知っているが、量子アニーリングマシンでの求解方法について、知らない方。
• Fixstars Amplify SDKの特徴について知りたい方。

Fixstars Amplify SDKについて

まず、今回扱うFixstars Amplify SDKについて、Fixstars社の公式ドキュメントでは、以下のように紹介されています。

Amplify SDK は株式会社フィックスターズの開発するイジングマシン向けミドルウェアライブラリです。

ここでイジングマシンというワードが登場しました。
Fixstars Amplify SDKを説明する前に、まず、前提知識として、イジングマシンは何かということについてお話します。
なお、もう理解しているよ！という方は、その次の章である「利用方法」まで飛ばしてください。

イジングマシン

イジングマシンとは、簡単にいうと、特定の最適化問題の計算に特化した仕組みを持った計算機の総称であり、具体例としては以下のマシンがあります。

• 量子アニーリングマシン
  • D-Wave 2000Q / Advantage / Leap Hybrid Solver
• 古典アニーリングマシン（シミュレーティッドアニーリング）
  • Fujitsu Digital Annealer / DA2 / DA3
  • Toshiba Simulated Bifurcation Machine
  • Hitachi CMOS annealing machine

この仕組みについてはまだまだ勉強中であり、説明できるほどの力を持ち合わせていないので、個別の説明は一旦置いておいて、このイジングマシンについて、組み合わせ最適化問題を解くうえで、把握しておくべき特徴は、以下の２点です。

• イジングマシンは入力形式を考慮して、特定の最適化問題を2値変数の2次多項式にする
• イジングマシンはこの２次多項式を最小化する、２値変数の組み合わせを求めること

２値変数とは{0,1}や{-1,1}など二つの値しかとらない変数のことを示しています。
以下の式は、２値変数の２次多項式の簡単な例となります。

 x_{1}x_{2}+x_{2}x_{3}+x_{3}x_{1}     　　　  (x_{1},x_{2},x_{3}=\{0,1\})

ちなみに、この式で定義される最小化問題を考えたときに、解（式を最小化する２値変数の組み合わせ）は $(x_1,x_2,x_3)=(0,0,0)$ となっています。この例は、簡単すぎますが、イジングマシンはこのように、2次多項式の値を最小にする2値変数の組み合わせを求めることに特化したマシンとなっています。そのため、組み合わせ最適化問題をこれらイジングマシンで実行する際は、1つの2値変数の2次多項式の形式で定式化を行う必要があります。

具体例：巡回セールスマン問題の定式化

この2値変数の2次多項式の形式で定式化ついて、今回扱う巡回セールスマン問題を例にとって、説明します。
ここで、巡回セールスマン問題とは、各地点の集合と各2地点間の移動コスト（たとえば距離）が与えられたとき、全ての都市をちょうど一度ずつ巡り出発地に戻る巡回路のうちで総移動コストが最小のものを求める組み合わせ最適化問題です。¹

1.　https://ja.wikipedia.org/wiki/%E5%B7%A1%E5%9B%9E%E3%82%BB%E3%83%BC%E3%83%AB%E3%82%B9%E3%83%9E%E3%83%B3%E5%95%8F%E9%A1%8C より引用

例えば以下の画像では、駅0～駅3の4駅に関して、コストとして各地点（駅）間の移動時間が与えられた時の、総移動時間が最小になる巡回セールスマン問題を示しており、実際には赤矢印で結ばれたルート（=総移動時間が最小になるルート）を求めることが目標となっています。

図 巡回セールスマン問題の問題設定と最適ルートのイメージ（図の駅間の○○分は各駅の移動時間を示す。）

この問題をイジングマシンで解く際のポイントとして、以下を2値変数の2次多項式で表現する必要があります。

• 目的関数：選ばれたルートの総コスト
• 制約条件：選ばれたルートは各駅を1回ずつ巡回していること

そこで、ここでは、以下の**4×4=16個の2値変数（バイナリ）**を導入することで、この巡回セールスマン問題を目的関数・制約条件の定式化していきたいと思います。

x_{ni}= \left\{\begin{array}{lll}
1 & (n番目に到着した都市はiである。)   \\
0 & (n番目に到着した都市はiではない。)
\end{array}
\right.   　　　　　　　　n, i = 0,1,2,3

いきなり、このような変数を並べられても、わかりずらいと思うので、上記の例（駅0～駅3の最適巡回路、赤矢印のルート）を使って説明したいと思います。この例では、**駅0→駅2→駅3→駅1（→駅0）**を順番に巡回するルートが示されていますが、この時、バイナリ変数$x_{ni}$のうち、1となる変数は以下の4変数です。

x_{00}, x_{12}, x_{23}, x_{31}

例えば、$x_{00}$は**「0番目（最初）に駅0に訪問するかどうか」を示す変数であり、上記ルートの通り、真のため値は1をとっています。逆に、$x_{01}$は「0番目（最初）に駅1に訪問するかどうか」**を示す変数ですが、こちらは偽のため値は0となっています。。
以下の図は、巡回ルートと各バイナリ変数の値の対応を示しています。

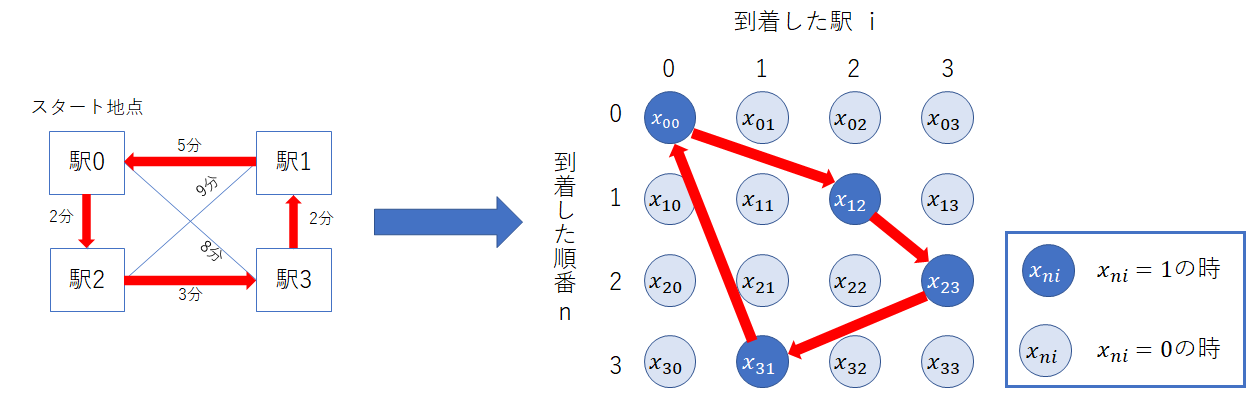
上記の画像の例ではすでに、コスト（総移動時間）が最適値をとるような、バイナリ変数の組み合わせが示されていますが、実際はこのような、バイナリ変数を用いて、目的関数・制約条件の定式化を行い、それをイジングマシンで求解し、バイナリ変数の値の組み合わせを求めるといった流れになります。
それでは、実際に目的関数・制約条件の定式化を行っていきます。

目的関数：選ばれたルートの総コスト

選ばれたルートの総和をバイナリ変数xを用いて定式化すると、以下のようになります。

\sum_{i,j}^{N-1}t_{ij}\sum_{n}^{N-1}x_{n,i}x_{n+1,j}\\

ここで$N$は総地点（今回は駅、$N=4$）数を示し、また、$t_{ij}$ は各駅間の移動時間を示しています。
※なお、目的関数内の$x_{n,i}x_{n+1,j}$に関して、$n=N-1$の時は $x_{N-1,i}x_{0,j}$ となるため、正確には、$x_{n,i}x_{(n+1)%N,j}$というのが正しい記述です。

制約条件：選ばれたルートは各駅を1回ずつ巡回していること

適切な求解を行うために、制約条件を設定する必要があります。
具体的には、「選ばれたルートは各駅を1回ずつ巡回していること」という制約をバイナリ変数で表現するために、以下2つの制約に分解します。

①各順番ごとに1都市のみ訪問する。
②ある駅の訪問は1回だけである。

それぞれの制約のイメージを以下の図に示します。
①, ②の制約がバイナリ変数$x_{ni}$を用いて、定式化できるということがわかると思います。

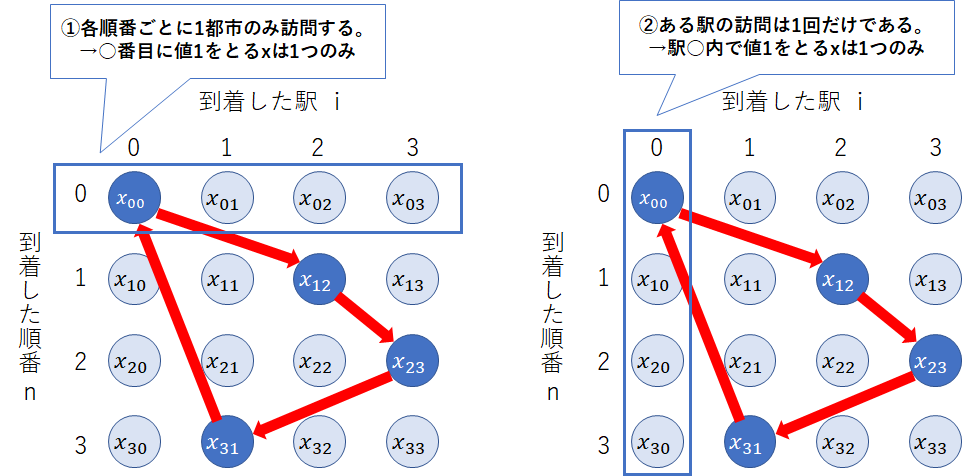
具体的に①、②の制約を式に表すと、以下の通りになります。

\sum_{i=0}^{N-1} x_{ni}=1　n=0,..,N-1　①\\
\sum_{n=0}^{N-1} x_{ni}=1　i=0,..,N-1　②

①は、「各順番で値1をとる変数は1つのみ ➡ 各順番ごとの変数の総和は1である。」と考えて、このような定式化がされています。②も同様に、「各駅で値1をとる変数は1つ ➡ 各駅ごとの変数の総和は1である。」といった考えに基づいています。

目的関数と制約条件を1つの2次多項式として定式化する

イジングマシンの入力のために、1つの2値変数の2次多項式を用意しなければならないため、上記の目的関数と制約条件を1つの式として、定式化する必要があります。
こちらは、いわゆる緩和問題として、制約条件を罰則項で実装したいと思います。つまり、制約条件の等式を満たさないときほど大きな値とるように変換して、目的関数とまとめたいと思います。

具体的には以下の式のようになります。

\sum_{i,j}^{N-1}t_{ij}\sum_{n}^{N-1}x_{ni}x_{nj} + A_{1}\sum_{n}^{N-1}(1-\sum_{i=0}^{N-1}x_{ni})^2+A_{2}\sum_{i}^{N-1}(1-\sum_{n=0}^{N-1} x_{ni})^2　\\

第1項は目的関数がそのまま反映されていますが、第2項 $\sum_{n}^{N-1}(1-\sum_{i=0}^{N-1}x_{ni})^2$ や第3項 $\sum_{i}^{N-1}(1-\sum_{n=0}^{N-1} x_{ni})^2$ はそれぞれ、制約条件①、②を変換した式となっています。
また、$A_1$、$A_2$は各罰則項の重み（値が大きいほど厳しい制約条件となる）を示しており、あらかじめ特定の値を決めておく必要があります。

このようにして、組み合わせ最適化問題をイジングマシンの入力形式として変換し、求解を行います。

ちなみに、このようなバイナリ変数でのイジングマシンの入力形式は**QUBO(Quadratic Unconstrained Binary Optimization)**と呼ばれています。また、バイナリ変数の代わりに、{-1,1}の2値をとる入力形式をイジング模型といいます。

多くの組み合わせ最適化問題は、これら、イジング模型やQUBOの形式で定式化可能といわれており、変数の数に制限はあるものの、イジングマシンで実行することができることが知られています。
参考：Ising formulations of many NP problems

Fixstars Amplify SDKの利用方法

かなり脱線してしまいましたが、イジングマシンやそれを用いた組み合わせ最適化問題の求解方法について、簡単に理解していただいたところで、次に利用方法について説明したいと思います。

公式のドキュメントによると、Fixstars Amplify SDKは以下の環境に対応しています。

• Ubuntu 16.04 / 18.04 / 20.04

• CentOS 7 / 8
• Windows 10 (WSL1/2)
• macOS Catalina 以降 / Big Sur (M1)

注意点としては、Windows PCで利用の場合は、[WSL1/2 (Windows Subsystem for Linux)] (https://docs.microsoft.com/ja-jp/windows/wsl/about)環境を構築する必要があります。

また、インターフェースとしてPythonを利用するため、そちらの環境構築を行っておく必要があります。

※ちなみに有料版ではC++の利用も可能だそうです。
詳細はhttps://amplify.fixstars.com/en/pricing をご覧ください。

これらの環境を用意したうえで、Fixstars Amplify SDKを利用するために、こちらの手順にもあるように、以下2つを行う必要があります。

行う必要があること	詳細手順
Amplifyアクセストークン取得	①https://amplify.fixstars.com/ja/register でユーザー登録を行う。 ②ログインするとアクセストークンが表示される。➡　完了！ ※後で使うので控えておく。
Fixstars Amplify SDKのインストール	①用意した環境上（Windowsの場合はWSL環境上）で 　pip install amplify　➡　完了！

Fixstars Amplify SDKの特徴

次にFixstars Amplify SDKの特徴について述べたいと思います。
主な特徴としては、以下の点が挙げられます。

①入力形式を意識せず定式化するのみで、実行できる。
②様々なイジングマシンをほぼ同じコードで実行できる。
③チュートリアルが豊富に用意されている。

それぞれの特徴について詳細に説明していきます。

①入力形式を意識せず定式化するのみで、実行できる。　

イジングマシンを利用して、組み合わせ最適化問題を解く際、定式化からイジングマシンの入力形式に落とし込むことが一つ煩わしい部分となります。

具体的には、以下に示す図の通り、通常のプログラミングでは、定式化したあと、論理モデル（イジングモデルやQUBO）への変換をし、その後、マシンの仕様や制限に合わせて変換を行い、はじめてマシンを実行できます。そのため、問題の定式化だけではなく、マシンへの入力形式も意識をする必要があります。

その一方で、Fixstars Amplify SDKでは、数式を表現する関数がいくつか用意されており、それをそのまま入力として、イジングマシンを実行できます。これにより、入力形式を意識せず、定式化するのみで、マシンを実行できます。

（https://amplify.fixstars.com/ja/sdk#functions より引用）

ここで、具体的な式に対するFixstars Amplify SDKの関数の例をいくつか紹介します。
まず、Σ(シグマ)による総和を表す式（例 $\sum_{n=0}^{N-1} x_{n}$)は以下のsum_polyで表現されます。

sum_poly([x[n] for i in range(N)]) 

また、等式制約（例 $x = 1$）は表される式は以下のequal_toで表現されます。

equal_to(x,1)

これらを組み合わせて、巡回セールスマン問題の目的関数や制約条件は以下のように表すことができます。（以下、Fixstars社の公式ドキュメントを参考にしたものになります。）

#目的関数
cost = sum_poly(
    N,
    lambda n: sum_poly(
        N,
        lambda i: sum_poly(
            N, lambda j: distances[i][j] * x[n][i] * x[(n + 1) % N][j]
        ),
    ),
)

# 制約：①各順番ごとに1駅にのみ訪問する。
row_constraints = [
    equal_to(sum_poly([x[n][i] for i in range(N)]), 1) for n in range(N)
]

# 制約：②ある駅の訪問は1回だけである。
col_constraints = [
    equal_to(sum_poly([x[n][i] for n in range(N)]), 1) for i in range(N)
]

#制約をまとめる。
constraints = sum(row_constraints) + sum(col_constraints)

上記のように、目的関数や制約条件を、可視性の高いコードとして、記述することができます。

また、イジングマシンで求解を行うために、これら目的関数や制約条件を入力形式（QUBO）で表される２次多項式として定式化してから、マシンを実行する必要がありますが、Fixstars Amplify SDKでは、これらを以下の1行で実現できます。

model = cost + A * constraints #Aは制約の強さ

あとは、このmodelを引数として、マシンを実行すれば、解を求めることができます。

このように、Fixstars Amplify SDKでは、定式化さえすれば、直感的かつ少ない行数のコードで、マシンを実行できるため、問題の定式化に集中できるということが一つメリットとして挙げられます。

②様々なイジングマシンをほぼ同じコードで実行できる。

Fixstars Amplify SDKによって、以下のイジングマシンを実行できます。

• Fixstars Amplify Annealing Engine
• D-Wave 2000Q / Advantage / Leap Hybrid Solver
• Fujitsu Digital Annealer / DA2 / DA3
• Toshiba Simulated Bifurcation Machine
• Hitachi CMOS annealing machine

こちらでも紹介されている通り、例えばFixstars Amplify Annealing Engineを利用して、求解を行う場合、以下のように記述します。簡単な実行の流れは、定式化(model)➡マシン設定(client)➡結果取得(result)となっています。
また、利用方法で説明した、アクセストークンについてはこのマシン設定部分のclient.tokenに設定する必要があります。

FixstarsAmplifyAnnealingEngineで実行

from amplify import Solver
from amplify.client import FixstarsClient

model = <--最小化する式（後で説明）-->

#FixstarsAmplifyAnnealingEngineを利用する際のパラメータ設定し、オブジェクトclientに格納
client = FixstarsClient()
client.token = "<Fixstarsのアクセストークン>" 

#マシンの設定
solver = Solver(client)

#model(最小化する式)を入力としてマシンを実行し、resultに求解結果を格納
result = Solver.solver(model)

一方で、 D-Wave 2000Qで記述する場合は、以下のようになります。
#変更点とコメントアウトされている部分がFixstars Amplify Annealing Engineと記述が異なる部分を示しています。

D-Wave2000Qで実行

from amplify import Solver
from amplify.client import DWaveClient　#変更点

model = <--最小化する式（後で説明）-->

# D-Wave 2000Qを利用する際のパラメータ設定し、オブジェクトclientに格納
client = DWaveClient()
client.token = "<Fixstarsのアクセストークン（D-Wave用）※>" 　#変更点
client.solver = "DW_2000Q_VFYC_6"　#変更点

#マシンの設定
solver = Solver(client)

#model(最小化する式)を入力としてマシンを実行し、resultに求解結果を格納
result = Solver.solver(model)

つまり、定式化部分、および結果取得部分のコードを変えずに、マシン設定部分を数行変更するだけで、実行するマシンを変更することができます。
※D-Waveを利用する際は、別途D-Wave用のアクセストークンをFixstarsに申請する必要があります。詳しくはユーザー登録後、閲覧できるマイページをご覧ください。

③日本語でのチュートリアルが豊富に用意されている。

こちらにあるように、公式の初心者向けのチュートリアルが、日本語で豊富に用意されています。また、実際の組み合わせ最適化問題などをAmplifyで求解したデモもいくつか用意されています。これらはともに、説明のほかにコードも示されているため、今まで、Fixstars Amplify SDKを触ったことのない方でも、簡単な実装であれば、すぐに行うことができます。

図 Amplify　ホームページに用意されているチュートリアル、オンラインデモの例
https://amplify.fixstars.com/ja/demo より引用

その他、詳細情報について知りたい方は公式ホームページやドキュメントをご覧ください。

実際に東京スカイツリーの撮影スポットの最適巡回ルートの求めてみる

問題設定

こちらで紹介されている東京スカイツリーの撮影スポットを１回ずつ訪問する際の最適ルートを実際に求めてみます。
とはいっても、それぞれの撮影スポット同士の距離を考えるのは少しややこしいので、今回はそれぞれの最寄り駅を1回ずつ訪問する場合を考えたいと思います。
具体的には、以下10駅です。

最寄り駅のリスト

stationList = ["押上", "錦糸町" ,"池袋", "とうきょうスカイツリー" ,"本所吾妻橋","浅草","南千住","月島" ,"船堀","市川"]

また、今回は最適ルートとして、最も巡回時間が短くなるようなルートを求めたいと思います。

データセット

下記を条件とし、鉄道各社が公開する時刻表をベースに移動時間行列を検討・作成しました。

• 2021年9月25日12:00 出発
• 手段は鉄道or徒歩
• 到着時間が最も早いルートの所要時間、運賃、乗換回数を取得

実行環境

今回は以下の環境で行いました。

• WSL2(Ubuntu)
• Python 3.8
• Visual Studio code
• Jupyter Notebook

手元にWindows10のPCのみしか用意できなかったため、今回はこのWindows10のPC上に、[WSL2 (Windows Subsystem for Linux)] (https://docs.microsoft.com/ja-jp/windows/wsl/about)環境(ubuntu)を構築しました。また、Fixstars Amplify SDKを利用のために、Python環境を用意する必要があり、先ほどのUbuntu上に、Pythonを導入しました。

また、コーディングはVScode+Jupyter Notebookを利用しました。

定式化

今回の問題は、巡回セールスマン問題として、考えることができます。そのため、この記事のイジングモデルの部分で説明したものと同様の手順で定式化を行い、求解を行いたいと思います。

今回の場合、合計10駅を１回ずつ訪問する際の所要時間の合計を最小にする巡回路を求める問題として、以下のように目的関数を定式化できます。
（再びの紹介となりますが、式やコードはFixstars社の公式ドキュメントを参考にしたものになります。）

\sum_{n=0}^{N-1}\sum_{i=0}^{N-1}\sum_{j=0}^{N-1} t_{ij}x_{ni}x_{n+1,j}　　\\

ここで、$t_{ij}$ は駅$i,j$ 間の所要時間を示します。また、$x_{nj}$の意味は以下の通りとなります。

x_{ni}= \left\{\begin{array}{ll}
1 & (n番目に到着した都市はiである。) \\
0 & (n番目に到着した都市はiではない。)
\end{array}
\right.

また、制約条件は以下のようになります。

\sum_{i=1}^{N-1} x_{ni}=1　　①\\
\sum_{n=1}^{N-1} x_{ni}=1　　②

ここで、①は各都市は１回ずつ訪問されること、②は同時には１つの都市にのみ訪問することを表しています。

それでは、上記の目的関数、および制約条件をFixstars Amplify SDKで実装します。
まず、必要な変数として、駅の総数を示す$N$（今回は10）と、N×Nのバイナリ変数$x$を定義します。

変数の定義

from amplify import BinaryPoly, SymbolGenerator

#Nは駅の総数（今回は10）
N = len(stationList)

#バイナリ変数xをN×N個として定義。
gen = SymbolGenerator(BinaryPoly) #バイナリー変数を生成するオブジェクトの定義
x = gen.array(N,N) #N×Nのバイナリ配列の生成

バイナリ変数の組は、SymbolGenerator(BinaryPoly) ➡ gen.array(N,N)で生成します。これにより、以下のような、N×Nの2次元配列として、バイナリ変数を生成します。

>>x
[[ q_0,  q_1,  q_2,  q_3,  q_4,  q_5,  q_6,  q_7,  q_8,  q_9],
 [q_10, q_11, q_12, q_13, q_14, q_15, q_16, q_17, q_18, q_19],
 [q_20, q_21, q_22, q_23, q_24, q_25, q_26, q_27, q_28, q_29],
 [q_30, q_31, q_32, q_33, q_34, q_35, q_36, q_37, q_38, q_39],
 [q_40, q_41, q_42, q_43, q_44, q_45, q_46, q_47, q_48, q_49],
 [q_50, q_51, q_52, q_53, q_54, q_55, q_56, q_57, q_58, q_59],
 [q_60, q_61, q_62, q_63, q_64, q_65, q_66, q_67, q_68, q_69],
 [q_70, q_71, q_72, q_73, q_74, q_75, q_76, q_77, q_78, q_79],
 [q_80, q_81, q_82, q_83, q_84, q_85, q_86, q_87, q_88, q_89],
 [q_90, q_91, q_92, q_93, q_94, q_95, q_96, q_97, q_98, q_99]]

※生成された配列xのクラスはAmplify SDKで提供されているBinaryPolyArrayクラスであり、NumPyのndarrayのような振る舞いをすると説明されています。
参考：https://amplify.fixstars.com/ja/docs/array.html

次に、定義した変数を用いて、目的関数、制約関数部分を記述します。
ここで、t に関しては、各駅間の移動時間を格納したリストとなっています。

目的関数と制約関数

from amplify import sum_poly

#目的関数
cost = sum_poly(
    N,
    lambda n: sum_poly(
        N,
        lambda i: sum_poly(
            N, lambda j: t[i][j] * x[n][i] * x[(n + 1) % N][j]
        ),
    ),
)

# 制約：①各順番ごとに1駅にのみ訪問する。
row_constraints = [
    equal_to(sum_poly([x[n][i] for i in range(N)]), 1) for n in range(N)
]

# 制約：②ある駅の訪問は1回だけである。
col_constraints = [
    equal_to(sum_poly([x[n][i] for n in range(ncity)]), 1) for i in range(N)
]

#制約条件をまとめる。
constraints = sum(row_constraints) + sum(col_constraints)

# 制約条件の強さを設定。
constraints *= np.amax(t)  

#制約条件と目的関数を、入力形式として定式化。
model = cost + constraints 

上記ソースのうち、costが目的関数を表しており、記事の冒頭で説明した通り、Σ（シグマ）表現は、sum_polyを、Σ（シグマ）の重ね合わせの表現はPythonの組み込み関数であるlambdaを用いて実装しています。また、制約条件①、②はそれぞれ、row_constraints、col_constraintsとして定義されており、等式制約の表現には、equal_toを利用しました。この際、x, n, i, jなど、各変数は前述の式（目的関数や制約条件①、②）の同名の変数と同じ使われ方をされています。

最終的にマシン実行の際の入力引数となるのが、modelとなっており、この時、制約条件の重みの値として、各駅間の移動時間を格納したリストtのうち、最大値であるnp.amax(t) を設定しました。このnp.amax(t) に関して、巡回路を形成する上で、目的関数にかかる重み（t）と比較して、制約条件①、②には強い重みをかける必要があったため、tの最大値であるnp.amax(t) を今回設定しました。

求解結果

定式化が済んだら、さっそく解いてみましょう。
この際、ユーザー登録時に取得したアクセストークンを記述します。

求解部分

from amplify import Solver
from amplify.client import FixstarsClient

#クライアントオブジェクトの設定
client = FixstarsClient()
client.token = "入手したアクセストークンを記入" 

#ソルバーオブジェクトを作成
solver = Solver(client)

#マシンの実行と求解結果の取得
result = solver.solve(model)

結果の取得に関しては、関数のsolve()を利用します。この関数によって、求解結果に関する様々な情報を格納したオブジェクトのリストを取得し、resultに格納しています。なお、このリストのデフォルトの要素数は1となっています。

※補足として、同じ最適コストをもたらすバイナリ変数の組み合わせが複数ある場合は、client.parameters.outputs.duplicate = Trueと設定することで、すべての組み合わせとその求解結果をsolve()で取得することができます。

そして、この取得したオブジェクトresult[0]の要素にアクセスすることで、具体的な、求解結果を得ることができます。例えば、result[0].energyには、求められた目的関数の最小値（総所要時間（分））が格納されています。

結果：最小値表示

energy = result[0].energy

>>energy
118.0

これは、求められたルートをたどる場合、その移動時間の合計は118分ということを示しています。

また、最適コストをもたらすバイナリ変数の組み合わせはresult[0].valuesで取得できます。

結果：最適ルート表示

values = result[0].values

>>values
{8: 0,
 87: 0,
 16: 0,
 95: 0,
 24: 0,
 32: 0,
 40: 0,
 48: 0,
 56: 0,
 64: 0,
 72: 1,
---省略----
}

しかし、上記のように、result[0].valuesは、キーがバイナリ変数のインデックス、値が0or1の辞書の形式となっており、少し見ずらいです。
そこで、便利なのがdecode_solution()で、第一引数に指定したリストなどの形式に、出力を整形してくれます。
具体的には、以下の通りです。第一引数にxを指定したことで、10×10の配列の形式での出力となっています。

結果：出力の整形

x_values = decode_solution(x, values)

>>x_values
array([[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
       [0., 0., 0., 0., 1., 0., 0., 0., 0., 0.],
       [1., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
       [0., 0., 0., 0., 0., 0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 0., 0., 0., 1., 0., 0.],
       [0., 0., 1., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 1., 0., 0., 0.],
       [0., 0., 0., 1., 0., 0., 0., 0., 0., 0.]])

その後、上記で整形した配列を用いて、実際に、求められた巡回ルートを駅名付きで表示します。

結果：ルート駅名表示

#x_valuesから1のみを抜き出し
route = np.where(np.array(x_values) == 1)[1]

#順番にルート表示
for stationIndex in route:
    print(stationList[stationIndex])

押上
錦糸町
市川
船堀
月島
池袋
南千住
とうきょうスカイツリー
浅草
本所吾妻橋

以上に示された通り、制約条件を満たす（各駅を１回ずつ訪問する）ルートを求めることができました。

※ちなみに、求まった最適解がすべての制約条件を満たさない場合、solve()関数はデフォルトで結果を出力しない（長さ0のリストを返す）設定となっています。
もし、すべての制約条件を満たさない場合でも解を出力してほしい場合はソルバーオブジェクトを作成後、"solver.filter_solution = False"を設定する必要があります。
参考：https://amplify.fixstars.com/ja/docs/solver.html

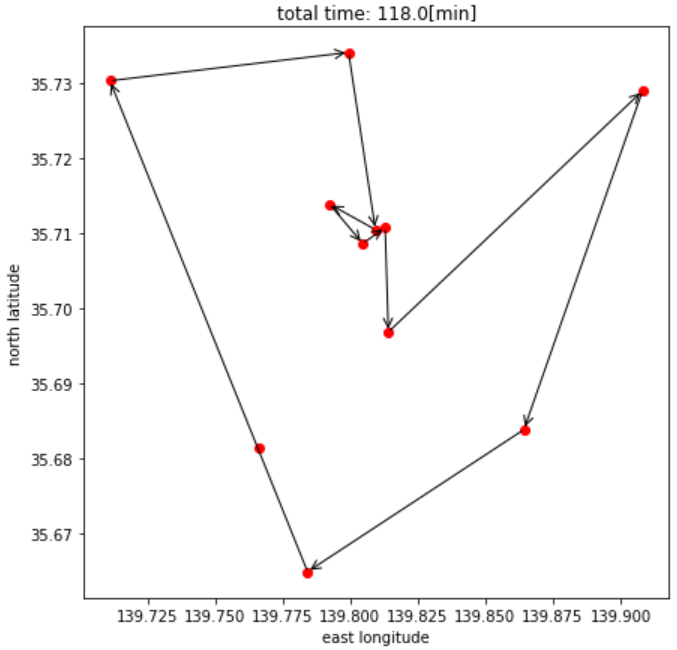
最後に、各駅の位置関係と求めたルートを可視化して、以下の図に反映させました。
この図の縦軸は各駅の北緯、横軸は東経を示しており、赤点が各駅の位置、黒矢印が求められたルートを示しています。

このように、各駅の位置関係で見ても、妥当なルートの構成ができたと思います。

制約を追加して、解いてみる。

上記のように、妥当そうなルートを求めることができましたが、これで終わりはつまらないので、いくつか制約を加えて、それを満たす最適ルートを求めたいと思います。
具体的には、以下の制約を加えたいと思います。

+「押上駅」と「とうきょうスカイツリー駅」を連続で訪問する。
+「東京駅」を最初の出発駅＆最後の到着駅に追加する。

「押上駅」と「とうきょうスカイツリー駅」を連続で訪問する

地図アプリなどで調べてみればわかると思いますが、この２つの駅はどう考えても徒歩圏内です。
それにも関わらず、上記ルートでは、押上駅ととうきょうスカイツリー駅は順番的には離れてしまっています。
そこで、この二つの駅を連続で訪問するような制約を加えたいと思います。
以下の式で表現される制約を追加しました。

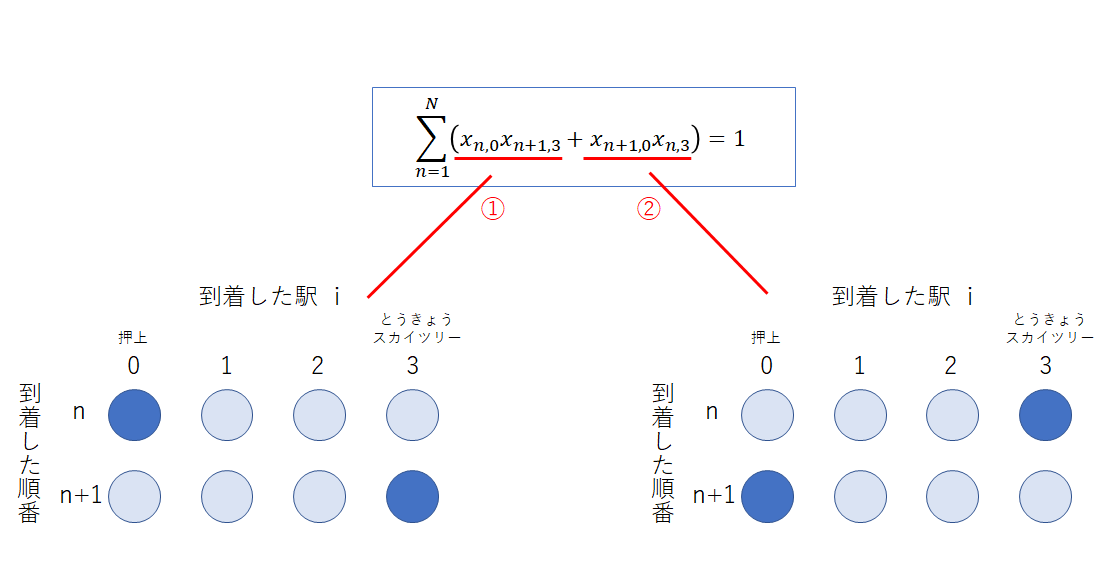
\sum_{n=1}^N (x_{n,0}x_{n+1,3}+x_{n+1,0}x_{n,3})=1　　(4)

以下の図に、上記制約のイメージを示します。

画像のように、この制約条件は、巡回ルートが次のいずれかを満たすように制限するものとなっており、各項がそれを表現しています。
①押上の次にとうきょうスカイツリーに訪問する。➡ $x_{n,0}x_{n+1,3}=1$ となる。
②とうきょうスカイツリーのつぎに押上に訪問する。➡ $x_{n+1,0}x_{n,3}=1$ となる。

この制約条件について、ソースコード上では、以下のように記述します。

routefix_constraints = [
    equal_to(sum_poly([x[n][0]*x[(n+1)%N][3]+x[n+1][0]*x[(n)%N][3]  for n in range(N)]), 1) 
]

「東京駅」を最初の出発駅＆最後の到着駅に追加する

ルートは求まったものの、スタート地点とゴール地点となる駅は、決めていませんでした。
そこで、新たに、最初の出発駅＆最後の到着駅として、東京駅を加えたいと思います。

まず、駅のリストに「東京駅」を追加します。また各駅との移動時間も改めて取得します。

stationList = ["押上", "錦糸町" ,"池袋", "とうきょうスカイツリー" ,"本所吾妻橋","浅草","南千住","月島" ,"船堀","市川","東京"]

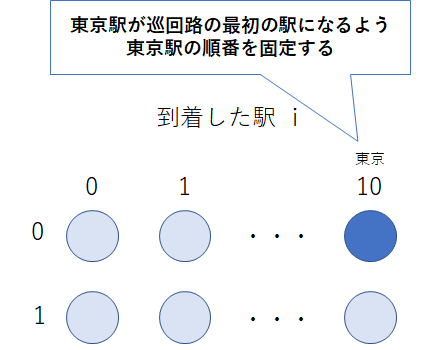
今回は巡回ルートを求める問題のため、最初の出発駅=最後の到着駅となるため、ここでは、東京駅が最初の出発駅となるような、以下の制約を追加します。制約のイメージは以下の画像に示しています。

x_{0,10}=1

上記の制約式をAmplifyで表すと、以下のようになります。

追加の制約条件

tokyo_constraints = [
   equal_to(q[0][10],1)
]

求解結果

先ほどと同様のコードで、求解結果を取得しました。
その結果は以下のようになります。

結果：最小値表示

>>result[0].energy
152.0

結果：ルート駅名表示

東京
南千住
押上
とうきょうスカイツリー
浅草
本所吾妻橋
錦糸町
市川
船堀
月島
池袋

以上のように、追加したものを含む、すべての制約を満たすようなルートを求めることができました！

まとめ

この記事では、Fixstars Amplify SDKの特徴をいくつか紹介した後、それを用いて、東京スカイツリーの撮影スポットの最適巡回ルートの求解を行ってみました。
再掲になりますが、この記事ではFixstars Amplify SDKの特徴として、以下3点を紹介しました。

①入力形式を意識せず定式化するのみで、実行できる。
②様々なイジングマシンをほぼ同じコードで実行できる。
③チュートリアルが豊富に用意されている。

実際に使ってみて、①の恩恵を特に感じました。今回は制約として、等式制約のみしか設定しませんでしたが、こちらにあるように、Fixstars Amplify SDKでは不等式制約や最小値制約など、さまざまな制約を表現する関数が用意されているので、興味がある人はぜひ使ってみてください。
また、③に関しては、チュートリアルのほかにも、公式のドキュメントが充実しており、初学者の私でも特に苦労することなく、マシンの実行を行うことができました。

最後に、なかなかボリュームのある記事となってしまいましたが、最後まで見てくださりありがとうございました。ご質問やご指摘等ありましたら、コメントまでお願いいたします。