はじめに
本記事は、Triplet Loss and Online Triplet Mining in TensorFlowを読んでTriplet Miningが何たるかの理解を深めるとともに、PytorchでOnline Triplet Miningの実装を試みたものです:)
↑の技術記事は、Olivier MoindrotさんによるTriplet Loss, Triplet Miningの解説と、TensorflowによるTriplet Minignの実装例が紹介されています。
ちなみに私がTriplet Loss & Triplet Miningを勉強して本記事にまとめた理由(モチベーション?)は、テキスト情報 & カテゴリラベルを持ったアイテム達に対して、その特徴や類似性を保持した埋め込みベクトルをいい感じ(?)に生成したいと思ったことです:)
もし気になった点や理解が誤っている箇所がありましたら、ぜひコメントいただけると喜びます:)
そもそもTriplet Lossとは?
Triplet Lossの始まり
Triplet Lossという方法論(損失関数)は、2015年にGoogleから出された顔画像認識の論文 A Unified Embedding for Face Recognition and Clusteringで初めて紹介されました。
この論文ではOnline Triplet Miningという方法を用いて、顔画像の埋め込みベクトルを学習する為の新しいアプローチについて述べています。
通常、教師あり学習による分類タスクでは、**固定数のクラス(ex. Aさん、Bさん、...)**があり、出力層の活性化関数としてソフトマックス関数、損失関数としてクロスエントロピー等を用いてネットワークを学習します。
しかし、場合によっては、クラスの数を可変にする必要があります。
例えば、顔認識において2つの未知の顔を比較して、同一人物の顔かどうかを判断する必要があります。
図. Triplet loss on two positive faces (Obama) and one negative face (Macron)
顔画像認識においてTriplet Lossは、各顔の特徴を表現する為のよりよい埋め込みベクトルを学習する為の方法です。
理想的な埋め込み空間では、同一人物の顔は近くにあり、異なる人物同士の埋め込みベクトル間ではよく分離したクラスタを形成しているはずです。
(つまり、同じ人物の複数の顔写真の埋め込みベクトルは似ているように、違う人物同士の埋め込みベクトル達は似ていないように、って事ですね...!
そして、上述した特徴を持った理想的な埋め込みベクトルを作る為に、Triplet Lossを活用できると!)
Triplet Lossの定義
Triplet Lossは損失関数の一種なので、定義式があります。
上のサブセクションで述べた様に、Triplet Lossを適用する目的は、生成される埋め込みベクトル達が以下の条件を満たすようにすることですよね。
- (条件1)同じラベルを持つ2つのサンプルは、埋め込み空間においてその埋め込みベクトル同士が近接している.
- (条件2)ラベルが異なる2つのサンプルでは、埋め込みベクトル同士が離れている。
この要件を定式化するために、Triplet Lossという損失関数は、以下のように**埋め込みベクトルのTriplet(i.e. 三つ組ですね!)**に対して定義されます。
- an anchor: アンカー. "メインの埋め込みベクトル"というイメージですかね...!
- a positive of the same class as the anchor: アンカーと同じラベルを持つ、ある一つの埋め込みベクトル
- a negative of a different class: アンカーと異なるラベルを持つ、ある一つの埋め込みベクトル
埋め込み空間(embedding space)における2つのベクトル間の距離を$d()$と表すと、Triplet(3つ組) $(a, p, n)$に関する損失関数$L$は以下の様に定義されます:
$$
L = \max(d(h_a,h_p) - d(h_a, h_n) + \text{margin}, 0)
$$
ここで$h_a, h_p, h_n$はそれぞれ、任意のTripletにおけるanchorの埋め込みベクトル、positiveの埋め込みベクトル、及びnegativeの埋め込みベクトルを表しています。
marginはハイパーパラメータで、大きく指定するほどクラス間の埋め込みベクトルの距離を広げさせるような定数だと理解しています。(理解が間違っていたらぜひ指摘してください...!)
上の損失関数を最小化する事で、$d(h_a,h_p)$を0に押し上げ(=条件1)、$d(h_a,h_n)$が$d(h_a,h_p) + \text{margin}$ よりも大きくなるように(=条件2)します。
Triplet lossの値に基づく3種類のTriplet
前のサブセクションで述べたTriplet lossの定義に基づき、Tripletを3つのカテゴリーに分ける事ができます。
-
easy triplets:
- $d(h_a,h_p) + \text{margin} < d(h_a,h_n)$により、損失が0になるtriplet.
-
hard triplets:
- 埋め込み空間において、negativeの方がpositiveよりもanchorに近いtriplet.
- i.e $d(h_a,h_n) <d(h_a,h_p)$
-
semi-hard triplets:
- 埋め込み空間において、positiveの方がnegativeよりもanchorに近いが、その差がmarginよりも小さい為、損失の値が正になるTriplet.
- i.e. $d(a,p) < d(a,n) < d(a,p) + \text{margin}$
また、この3つのカテゴリーの定義はそれぞれ、anchorとpositiveに対するnegativeの相対的な位置関係によって決まります。
したがって、Tripletの3つのカテゴリをnegativeの位置の3つのカテゴリに拡張して、hard negative、semi-hard negative、easy negativeと表す事もできます。
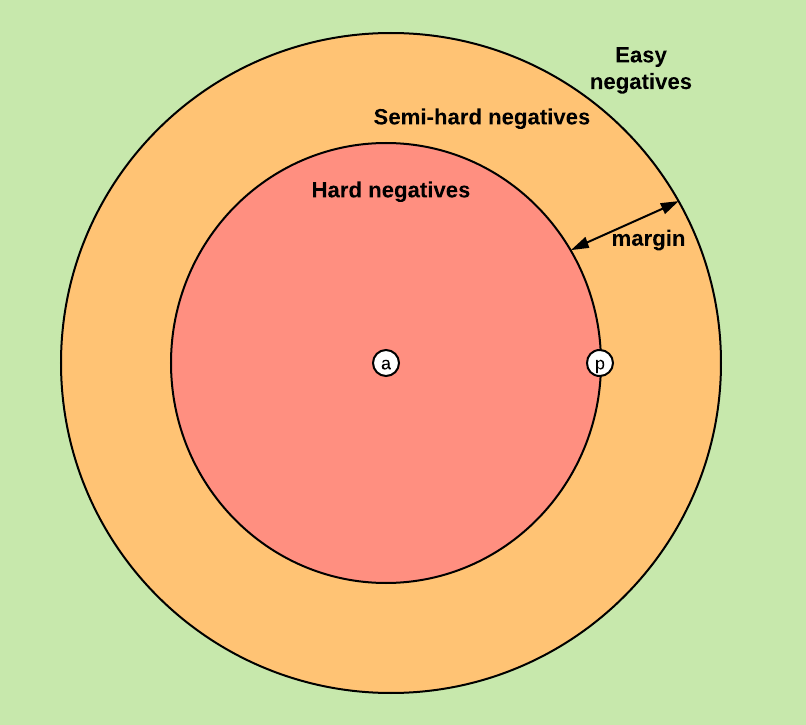
下図は、「anchorとpositiveに対するnegativeの相対的位置」に対応する、埋め込み空間の3つの領域を示しています。下図においてnegativeがどこに置かれるかによって、Tripletのカテゴリが一つに定まるという事ですね...!
図. anchorとpositiveが与えられた状態でのnegativeの相対的位置と、三種類のTripletカテゴリ(=negativeカテゴリ)の関係
どのようなTripletで学習させるかは、測定値に大きく影響します。
Tripletの元祖であるFacenet論文では、anchorとpositiveのペアごとにランダムにsemi-hardなnegativeを選び、これらのTripletで学習しています。
Triplet Mining
上のセクションで、**埋め込みベクトルのTriplet(3つ組)に対する損失関数(i.e. Triplet Loss)**を定義し、定義式を元にTripletを三種類のカテゴリに分類、そしてあるTripletは他のTripletよりも学習に有用であることを見てきました。
問題は、これらのTripletをどのようにサンプリングするか、つまり「マイニング」するかです。
Triplet MiningはOfflineとOnlineの大きく二種類に分かれます.
Offline triplet mining
Offline Triplet Miningでは、例えば各エポックの最初に、オフラインでトリプレットを見つけます。
学習セット上のすべての埋め込みベクトルを計算し、hardまたはsemi-hardなTripletのみを選択します。
そして、これらのTripletを用いて1つのエポックの学習を実行します。
具体的には、Tripletのリスト$(i,j,k)$を作成します。(i.e. 埋め込みベクトルを計算する前に、予め考えられるTripletを取得している事がオフラインの特徴っぽい...!)
つまり、$B$個のTripletを得るために$3B$個の埋め込みベクトルを計算し、これらの$B$個のTriplet Lossを計算し、モデルを更新させる必要があります。
この手法は、トリプレットを生成するためにトレーニングセットをフルパスする(i.e. パラメータ更新の度に全レコードを一旦モデルに通して埋め込みベクトルを取得するってこと??)必要があるため、全体としてあまり効率的ではありません。また、オフラインでマイニングされたTripletを定期的に更新する必要があります。
Online triplet mining
一方、Online triplet miningはFacenetで導入され、Brandon Amosのブログ記事OpenFace 0.2.0: Higher accuracy and halved execution timeでよく説明されています。
Online triplet miningのアイデアは、入力のバッチごとに、有用なTripletをその場で計算することです。
B$個の例(例えば顔画像)が与えられたら、先に$B$個の埋め込みベクトルを計算し、最大$B^3$個のTripletを見つけます。もちろん、これらのTripletのほとんどは、**有効(valid)**ではありません.(=anchor & positive & negativeの関係性を満たさない.)
オフライン手法と比べて、オンライン手法では$B$個の埋め込みベクトルを計算したのち、それらの値を元にTripletを選ぶので、計算量的により効率的なアプローチです。
図. Online triplet miningによるTriplet Lossの計算
Online triplet miningにおける戦略
Online triplet miningでは、$B$個の入力データから$B$個の埋め込みベクトルを一括して計算します。次に重要なのが、これらの**$B$個の埋め込みベクトルを考慮して、どのようにTripletを生成するか**(選ぶか)です。
まず、1 batchの入力データにおいてi,j,kの3つのインデックスを指定します。
$i$と$j$が同じラベルを持ち、$i$と$k$が異なるラベルであれば、$(i,j,k)$はValid(有効な) Tripletであると言えます。
(この時点で$B^3$個からだいぶ削れるはず...!)
ここで残るのは、「Valid(有効な) Triplet達の中から、どのように実際に損失を計算し学習に活用するTripletを選ぶべきか」ですよね。
↑に関する戦略のうち2つについては、論文「In Defense of the Triplet Loss for Person Re-Identification」の第2節に詳しい説明があるそうです。(私はまだこの技術記事しか読んでいません...!)
入力データとして、$B = PK$個の顔画像のバッチがあり、$P$人の異なる人物からなり、それぞれ$K$枚の画像があると仮定しましょう。
例えば$K=4$です。このとき、2つの戦略があります: batch all storategyとbatch hard storategyです。
batch all storategy
- batch all storategyでは、有効なトリプレットをすべて選択し、その上でhardおよびsemi-hardなTripletの損失を平均化します。
- ここで重要なのは,easyなtriplet(損失=0 のTriplet)を考慮しないことです。
- なぜなら、これらのTripletを含めて平均化すると、全体の損失が非常に小さくなるからです。
- batch all storategyにより合計 $PK \times (K-1) \times (PK-K)$ 個のTripletが生成されます
- ($PK$ 個のanchor、1つのanchorあたり $K-1$ 個のpositive、 $PK-K$ 個のnegative)。
- (実際にはここから更にeasy tripletを取り除くので、更に少なくなる。)
batch hard storategy
- batch hard storategyでは、$B=PK$個の各anchorについて、バッチの中で最もhardなpositiveと、最もhardなnegativeを選択します。
- 最もhardなpositive = (i.e 距離 $d(h_a,h_p)$が最大)
- 最もhardなnegative = (i.e. 距離 $d(a,p)$が最小)
- 即ち↑の方法で選択されたtripletは、各anchorにおいて最もhardな(損失が大きい)tripletです。
- batch hard storategyで生成(選択)されるtripletの数は、$B=PK$個です。
- 最終的には$B=PK$個のTriplet Lossを平均化したものを用います。
なお上述した論文によると、batch hard storategyが最も良い性能を発揮するとの事です。ただこの結論はデータセットに依存するものであり、開発におけるTriplet Miningの戦略は、実際のデータセットを用いてパフォーマンスを比較することによって決定されるべきものであるとも述べています。
Online Triplet Mining をPytorchで実装してみた
それでは、tensorflowによるtriplet miningの実装を参考にしつつ、pytorchで実装し直してみます。
ソースコードは以下のリンクにおいてあります。
埋め込みベクトル間の距離を効率的に算出する
Triplet Lossの値は埋め込みベクトルの距離 $d(h_a, h_p)$ と $d(h_a, h_n)$ に依存するので、まず、埋め込みベクトル達の距離行列を効率的に計算する必要があります。ユークリッドノルムと二乗ユークリッドノルムについて、 calc_pairwise_distances 関数として実装します。
import torch
from torch import Tensor
def calc_pairwise_distances(embeddings: Tensor, is_squared: bool = False) -> Tensor:
"""compute distances between all the embeddings.
Parameters
----------
embeddings : Tensor
tensor of shape (batch_size, embed_dim)
is_squared : bool, optional
If true, output is the pairwise squared euclidean distance matrix.
If false, output is the pairwise euclidean distance matrix.,
by default False
Returns
-------
Tensor
pairwise_distances: tensor of shape (batch_size, batch_size)
行列の各要素に、2つのembedding vector間の距離が入っている.
"""
dot_product_matrix = torch.matmul(
input=embeddings,
other=embeddings.t(),
) # ->各ベクトル間の内積を要素とした行列
squared_embedding_norms = dot_product_matrix.diag().unsqueeze(dim=1) # 対角要素(=各ベクトルの長さの二乗)を取り出す
# euclidean distance(p, q) = \sqrt{|p|^2 + |q|^2 - 2 p*q}
euclidean_distances = squared_embedding_norms + squared_embedding_norms.t() - 2 * dot_product_matrix # ユークリッド距離を算出
if not is_squared:
return torch.sqrt(euclidean_distances)
return euclidean_distances
valid Triplet/invalid tripletを判定させる
続いて、各Triplet(バッチ内の任意の3つの組み合わせ)に対して、valid(有効な) tripletか否かを判定する処理をTripletValidetorクラスに実装します。
get_valid_maskメソッドでは、引数でバッチ内の全てのデータのラベルのTensor(batch_size1)を受け取り、返り値として有効な(valid) triplet(i,j,k)->True, 無効な(invalid) triplet(i,j,k)->FalseとなるようなTensor(batch_sizebatch_size*batch_size)を返します。
最終的にはこのbool Tensorを距離行列に乗じたりする事で、invalid tripletを取り除くmaskとしての使い方を想定しています。
class TripletValidetor:
"""tripletが有効か無効かを判定する為のクラス"""
def __init__(self) -> None:
pass
def get_valid_mask(self, labels: Tensor) -> Tensor:
"""有効な(valid) triplet(i,j,k)->True, 無効な(invalid) triplet(i,j,k)->Falseとなるような
Tensor(batch_size*batch_size*batch_size)を作成して返す.
Return a 3D mask where mask[i, j, k]
is True iff the triplet (i, j, k) is valid.
A triplet (i, j, k) is valid if:有効なtripletである条件は以下の2つ:
- i, j, k are distinct
- labels[i] == labels[j] and labels[i] != labels[k]
Parameters
----------
labels : Tensor
int32 `Tensor` with shape [batch_size]
return:Tensor
shape = (batch_size, batch_size, batch_size)
mask[i, j, k] は $(i,j,k)$ が有効なトリプレットであれば真
"""
# 条件1:Check that i, j and k are distinct 独立したindicesか否か
is_not_distinct_matrix = torch.eye(n=labels.size(0)).bool() # labelsのサイズに応じた単位行列を生成し、bool型にキャスト
is_distinct_matrix = ~is_not_distinct_matrix # boolを反転する
i_not_equal_j = is_distinct_matrix.unsqueeze(dim=2)
i_not_equal_k = is_distinct_matrix.unsqueeze(dim=1)
j_not_equal_k = is_distinct_matrix.unsqueeze(dim=0)
is_distinct_triplet_tensor = i_not_equal_j & i_not_equal_k & j_not_equal_k
# 条件2: Check if labels[i] == labels[j] and labels[i] != labels[k]
is_label_equal_matrix = labels.unsqueeze(0) == labels.unsqueeze(1)
i_equal_j = is_label_equal_matrix.unsqueeze(2)
i_equal_k = is_label_equal_matrix.unsqueeze(1)
is_valid_labels_triplet_tensor = i_equal_j & (~i_equal_k)
return is_distinct_triplet_tensor & is_valid_labels_triplet_tensor
def get_anchor_positive_mask(self, labels: Tensor) -> Tensor:
"""各要素がboolの2次元のTensorを返す. anchor * positiveのペアならTrue, それ以外はFalse
Return a 2D mask where mask[a, p] is True,
if a and p are distinct and have same label.
Parameters
----------
labels : Tensor
with shape [batch_size]
Returns
-------
Tensor
bool Tensor with shape [batch_size, batch_size]
"""
# 条件1: iとjがdistinct(独立か)を確認する
is_not_distinct_matrix = torch.eye(n=labels.size(0)).bool()
is_distinct_matrix = ~is_not_distinct_matrix # boolを反転する
# 条件2: labels[i]とlabels[j]が一致しているか否かを確認する
is_label_equal_matrix = labels.unsqueeze(0) == labels.unsqueeze(1)
# 条件1と条件2をcombineして返す
return is_distinct_matrix & is_label_equal_matrix
def get_anchor_negative_mask(self, labels: Tensor) -> Tensor:
"""各要素がboolの2次元のTensorを返す. anchor * negativeのペアならTrue, それ以外はFalse
Return a 2D mask where mask[a, n] is True,
if a and n have distinct labels.
Parameters
----------
labels : Tensor
with shape [batch_size]
Returns
-------
Tensor
bool Tensor with shape [batch_size, batch_size]
"""
# 条件1: iとjがdistinct(独立か)を確認する
is_not_distinct_matrix = torch.eye(n=labels.size(0)).bool()
is_distinct_matrix = ~is_not_distinct_matrix # boolを反転する
# 条件2: labels[i]とlabels[j]が一致していないか否かを確認する
is_not_label_equal_matrix = labels.unsqueeze(0) != labels.unsqueeze(1)
# 条件1と条件2をcombineして返す
return is_distinct_matrix & is_not_label_equal_matrix
batch all storategyを実装
では、上で定義したcalc_pairwise_distances関数とTripletValidetorクラスを用いて、BatchAllStrategyクラスを定義します。
使い方としては、Pytorchによるtrain関数の中で、1 batch毎のdataset(embeddingベクトル & 対応するラベル)を取得した後、BatchAllStrategyオブジェクトを初期化、calc_triplet_loss()メソッドにembeddingベクトル & 対応するラベルを入力して出力としてtriplet lossを取得します。
取得したtriplet lossを損失関数としてBack Propagationする事で、モデルを更新します。
from typing import Tuple
import numpy as np
import torch
from torch import Tensor
from src.triplet_mining.pairwise_distances import calc_pairwise_distances
from src.triplet_mining.valid_triplet import TripletValidetor
class BatchAllStrategy:
def __init__(
self,
margin: float,
squared: bool = False,
) -> None:
"""
- margin : float
margin for triplet loss
- squared : bool, optional
If true, output is the pairwise squared euclidean distance matrix.
If false, output is the pairwise euclidean distance matrix.,
by default False
"""
self.margin = margin
self.squared = squared
self.triplet_validetor = TripletValidetor()
def calc_triplet_loss(
self,
labels: Tensor,
embeddings: Tensor,
) -> Tuple[Tensor, Tensor]:
"""Build the triplet loss over a batch of embeddings.
We generate all the valid triplets and average the loss over the positive ones.
Parameters
----------
labels : Tensor
labels of the batch, of size (batch_size,)
embeddings : Tensor
tensor of shape (batch_size, embed_dim)
Returns
-------
Tuple[Tensor, Tensor]
triplet_loss: scalar tensor containing the triplet loss
fraction_positive_triplets: scalar tensor containing 有効なtripletに対するpositive(i.e. not easy) tripletsの割合
"""
pairwise_distance_matrix = calc_pairwise_distances(embeddings, is_squared=self.squared)
triplet_loss = self._initialize_triplet_loss(pairwise_distance_matrix)
valid_triplet_mask = self.triplet_validetor.get_valid_mask(labels)
triplet_loss = self._remove_invalid_triplets(triplet_loss, valid_triplet_mask)
triplet_loss = self._remove_negative_loss(triplet_loss)
num_positive_triplets = self._count_positive_triplet(triplet_loss)
num_valid_triplets = torch.sum(valid_triplet_mask)
fraction_positive_triplets = num_positive_triplets / (num_valid_triplets + 1e-16)
# -> 有効なtripletに対するnot easy tripletsの割合
# Get final mean triplet loss over the positive valid triplets
triplet_loss_mean = torch.sum(triplet_loss) / (num_positive_triplets + 1e-16)
return triplet_loss_mean, fraction_positive_triplets
def _initialize_triplet_loss(self, pairwise_distance_matrix: Tensor) -> Tensor:
"""triplet_loss(batch_size*batch_size*batch_sizeの形のTensor)の初期値を作る.
各要素がtriplet_loss(i,j,k),
一旦、全てのi,j,kの組み合わせでtriplet_lossを計算する
"""
anchor_positive_dist = pairwise_distance_matrix.unsqueeze(dim=2)
# -> (batch_size, batch_size, 1)
anchor_negative_dist = pairwise_distance_matrix.unsqueeze(dim=1)
# -> (batch_size, 1, batch_size)
# Compute a 3D tensor of size (batch_size, batch_size, batch_size)
# triplet_loss[i, j, k] will contain the triplet loss of anchor=i, positive=j, negative=k
# Uses broadcasting where the 1st argument has shape (batch_size, batch_size, 1)
# and the 2nd (batch_size, 1, batch_size)
return anchor_positive_dist - anchor_negative_dist + self.margin
def _remove_invalid_triplets(self, triplet_loss: Tensor, valid_triplet_mask: Tensor) -> Tensor:
"""triplet lossのTensorから、有効なtripletのlossのみ残し、無効なtripletのlossをゼロにする"""
masks_float = valid_triplet_mask.float() # True->1.0, False->0.0
return triplet_loss * masks_float # アダマール積(要素積)を取る
def _remove_negative_loss(self, triplet_loss: Tensor) -> Tensor:
"""triplet lossのTensorから、negative(easy) triplet lossをゼロにし、positive(hard)なlossの要素のみ残す.
negative(easy)なtriplet loss= triplet lossが0未満の要素.
Remove negative losses (i.e. the easy triplets).
"""
return torch.max(
input=triplet_loss,
other=torch.zeros(size=triplet_loss.shape),
)
def _count_positive_triplet(self, triplet_loss: Tensor) -> Tensor:
"""triplet_lossのTensorの中で、positive(i.e. not easy) triplet lossの要素数をカウントして返す
Count number of positive triplets (where triplet_loss > 0)
"""
valid_triplets = torch.gt(input=triplet_loss, other=1e-16)
valid_triplets = valid_triplets.float() # positive triplet->1.0, negative triplet->0.0
return torch.sum(valid_triplets)
batch hard storategyを実装
BatchAllStrategyと同様に、calc_pairwise_distances関数とTripletValidetorクラスを用いて、BatchHardStrategyクラスを定義します。
class BatchHardStrategy:
def __init__(
self,
margin: float,
squared: bool = False,
) -> None:
self.margin = margin
self.squared = squared
self.triplet_validetor = TripletValidetor()
def calc_triplet_loss(
self,
labels: Tensor,
embeddings: Tensor,
) -> Tensor:
"""Build the triplet loss over a batch of embeddings.
For each anchor, we get the hardest positive and hardest negative to form a triplet.
Args:
labels: labels of the batch, of size (batch_size,)
embeddings: tensor of shape (batch_size, embed_dim)
Returns:
triplet_loss: scalar tensor containing the triplet loss
"""
pairwise_distance_matrix = calc_pairwise_distances(embeddings, is_squared=self.squared)
hardest_positive_dists = self._extract_hardest_positives(pairwise_distance_matrix, labels)
hardest_negative_dists = self._extract_hardest_negatives(pairwise_distance_matrix, labels)
init_triplet_loss = hardest_positive_dists - hardest_negative_dists + self.margin
triplet_loss = torch.max(
input=init_triplet_loss,
other=torch.zeros(size=init_triplet_loss.shape),
) # easy tripletを取り除く.
# Get final mean triplet loss
triplet_loss_mean = torch.mean(triplet_loss)
return triplet_loss_mean
def _extract_hardest_positives(
self,
pairwise_distance_matrix: Tensor,
labels: Tensor,
) -> Tensor:
"""各anchorに対して、hardest positiveを見つける.
For each anchor, get the hardest positive.
1. 有効なペア(anchor,positive)の2次元マスクを取得する
2. 修正(有効なペアのみ考慮)された、距離行列の各行に対する最大距離を取る
返り値は、Tensor with shape (batch_size, 1)
"""
is_anchor_positive_matrix = self.triplet_validetor.get_anchor_positive_mask(
labels,
)
is_anchor_positive_matrix_binary = is_anchor_positive_matrix.float()
pairwise_dist_matrix_masked = torch.mul(
pairwise_distance_matrix,
is_anchor_positive_matrix_binary,
) # アダマール積(要素毎の積)
hardest_positive_dists, _ = pairwise_dist_matrix_masked.max(
dim=1, # dim番目の軸に沿って最大値を取得
keepdim=True, # 2次元Tensorを保つ
) # ->Tensor with shape (batch_size, 1)
return hardest_positive_dists
def _extract_hardest_negatives(
self,
pairwise_distance_matrix: Tensor,
labels: Tensor,
) -> Tensor:
"""各anchorに対して、hardest negativeを見つける.
For each anchor, get the hardest negative.
1. 有効なペア(anchor, negative)の2次元マスクを取得する.
2. 無効なペアを考慮から取り除く為に、無効なペアのdistanceに各行の最大値を足す.
3. 距離行列の各行に対する最小距離を取る
返り値は、Tensor with shape (batch_size, 1)
"""
is_anchor_negative_matrix = self.triplet_validetor.get_anchor_negative_mask(
labels,
)
is_anchor_negative_matrix_binary = is_anchor_negative_matrix.float()
max_dist_each_rows, _ = pairwise_distance_matrix.max(
dim=1,
keepdim=True,
) # 各行の最大値を取得
pairwise_dist_matrix_masked = pairwise_distance_matrix + (
max_dist_each_rows * (1.0 - is_anchor_negative_matrix_binary)
) # is_anchor_negative=Falseの要素にmax_distを足す
hardest_negative_dists, _ = pairwise_dist_matrix_masked.min(dim=1, keepdim=True)
return hardest_negative_dists
テストコード
上述した各処理にテストコードを追加しました。
以下のリンクから参照できます。
https://github.com/morinota/ConvMF/tree/main/test/triplet_mining
なお、テストデータはTriplet Loss and Online Triplet Mining in TensorFlowの実装をそのまま取ってきています。
以下のコマンドで実行できます。
pytest テストコードのファイルパス
きちんとテストコードも書いているなんて、我ながら素敵だな-と思います:)
これで安心してリファクタリングできるぞ...!
おわりに
本記事では、pytorchでonline triplet miningの2つの戦略batch all & batch hard storategyをpytorchで実装してみました。
自分で調べた際にtriplet miningに関する日本語記事やpytorchによる実装例がなかなか発見できなかったので、私と同様にtriplet lossを活用したいと考える方の情報収集に少しでもプラスの影響を与えられたら幸いです:)
このtriplet loss & triplet miningを活用して、アイテムの特徴や類似性をより良い感じ(?)に表現する埋め込みベクトルをつくっていくぞ...!!
もし気になった点や理解が誤っている箇所がありましたら、ぜひコメントいただけると喜びます:)