More than 3 years have passed since last update.

【Go】Tree (木構造)

Last updated at 2021-06-01Posted at 2021-05-08

Goでプログラミングの基礎を学ぶシリーズ

スクールでは教えてくれないプログラミングの基礎、データ構造とアルゴリズムをGoで学んでいくシリーズです。
そのデータ構造がどのようなものであるかは、理解を助けてくれるサイトを紹介しつつ、簡単な説明に留めさせていただきます。(ご自身でも調べてみてください！)
筆者自身、Exerciseに取り組みながら理解を深めていったので、コードの解説を中心に記事を書いていきたいと思います。

	タイトル
#0	はじめに (環境構築と勉強方法)
#1	Pointer, Array, String (ポインタと配列と文字列と)
#2	File operations (ファイル操作)
#3	Linked List (連結リスト)
#4	Stack & Queue (スタックとキュー)
#5	Search algorithms (探索アルゴリズム)
#6	Tree (木構造) ☜ here
#7	Sorting algorithms (ソートアルゴリズム)
#8	String pattern matching algorithms (文字列探索アルゴリズム)

今回は**#6 Tree (木構造)**です。

Treeとは

Tree (木構造) とは、読んで字の通り、木のような構造のデータ構造のことです。
Linked List (連結リスト) が線型構造であったのに対し、 Tree は階層構造をとることができます。
Wikipediaを参考に、主な用語をあげておきます。

英語	日本語	意味
child node	子ノード	木構造の各ノードは0個以上の子ノードを持つ
parent node	親ノード	子ノードを持つノード
root node	根ノード	親ノードを持たないノード。根ノードは木構造の最上位にあるノードであり、1つの木構造に1つしか存在しない。
leaf node	葉ノード	子ノードを持たないノード。木構造の下位の末端にあるノードであり、1つの木構造に複数存在しうる。
internal node	内部ノード	子ノードを持つノード。根ノードと葉ノード以外のノードをさす。
sub tree	部分木	木構造の一部であり、それ自身も完全な木構造となっている部分をさす

Binary Tree (二分木)

Binary Tree は Tree の中でも、一つの node が持つ　child node の数が 2以下 の Tree です。

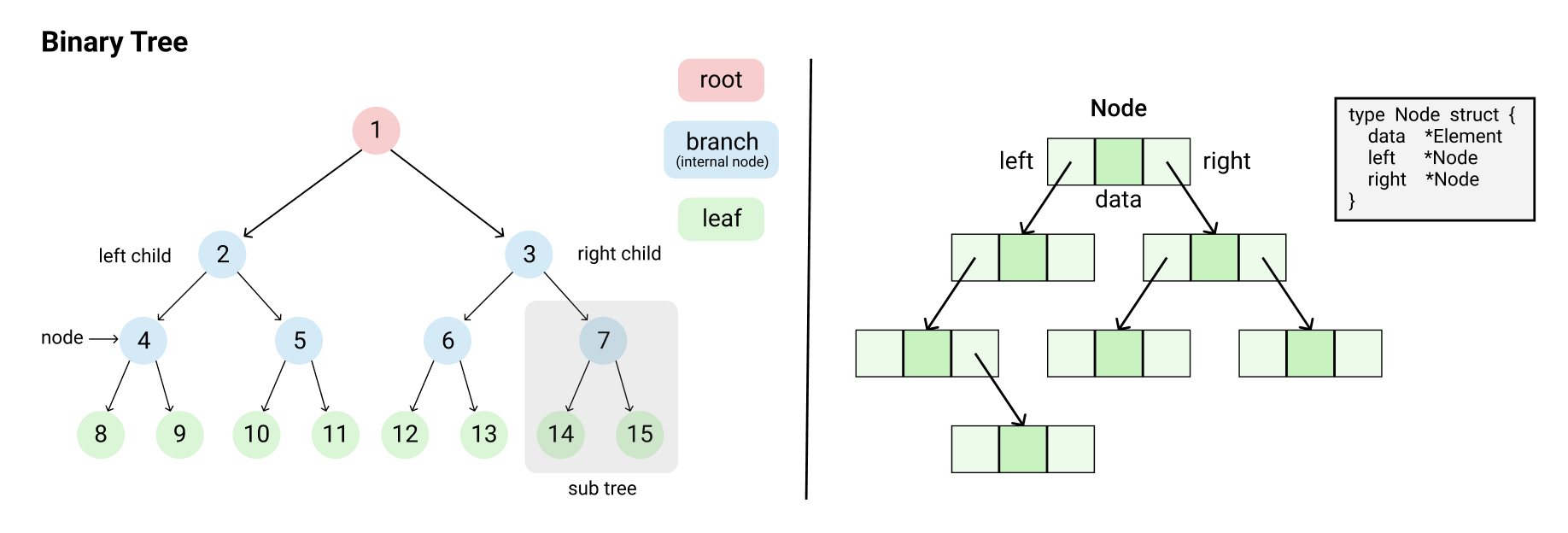
左は Tree の構造と各名称を図示し、右は Node のリンクを図示しました。
ここから、Binary Tree でよく使われる重要な関数をみていきます。

IsEmptyTree

func (t *Tree) IsEmptyTree() bool {
	return t.root == nil
}

Tree が空かどうかの判定なので、 root が nil かどうかを返します。

IsLeaf

func IsLeaf(node *Node) bool {
	if node == nil {
		return true
	}
	return node.left == nil && node.right == nil
}

引数で渡ってきた node が leaf であるかどうかを判定します。

ChildTree

func (n *Node) ChildTree() *Tree {
	if n == nil {
		return nil
	}
	return &Tree{root: n}
}

ある node を root とする Tree を返します。
sub tree を1つの Tree として扱っているような感じですね。
CountNodes などの　Recursive function (再帰関数)　で使われます。

CountNodes

func (t *Tree) CountNodes() int {
	if t == nil || t.root == nil {
		return 0
	}
	if IsLeaf(t.root) {
		return 1
	}
	return 1 + t.root.left.ChildTree().CountNodes() + t.root.right.ChildTree().CountNodes()
}

Tree を構成する node の数をカウントします。
return で、 count を +1 することと、 root.left および root.right がそれぞれ　root となった　Tree に対して、CountNodes をしています。

CountLeafs

func (t *Tree) CountLeafs() int {
	if t == nil {
		return 0
	}
	if IsLeaf(t.root) {
		return 1
	}
	return t.root.left.ChildTree().CountLeafs() + t.root.right.ChildTree().CountLeafs()
}

leaf の数をカウントします。

CountNonLeafNodes

func (t *Tree) CountNonLeafNodes() int {
	if t == nil {
		return 0
	}
	if IsLeaf(t.root) {
		return 0
	}
	return 1 + t.root.left.ChildTree().CountNonLeafNodes() + t.root.right.ChildTree().CountNonLeafNodes()
}

leaf ではない node の数をカウントします。

Binary Search Tree (二分探索木)

構造は Binary Tree と変わりませんが、 Left nodes の値 < root node の値 < Right nodes の値 という制約をもちます。
操作として、 Search (探索), Insert (挿入), Delete (削除) があります。

Search

func (t *Tree) SearchNode(x Element) *Node {
	if t == nil {
		return nil
	}
	if t.root.data == x {
		return t.root
	}
	if t.root.data < x {
		return t.root.right.ChildTree().SearchNode(x)
	} else {
		return t.root.left.ChildTree().SearchNode(x)
	}
}

Insert

func (t *Tree) InsertNode(x Element) {
	node := &Node{data: x}
	if t.root == nil {
		t.root = node
	} else {
		if t.root.data < x {
			if rightChild := t.root.right.ChildTree(); rightChild != nil {
				rightChild.InsertNode(x)
			} else {
				t.root.right = node
			}
		} else {
			if leftChild := t.root.left.ChildTree(); leftChild != nil {
				leftChild.InsertNode(x)
			} else {
				t.root.left = node
			}
		}
	}
}

Delete

Delete は処理が少し複雑です。
Search や Insert と異なり、削除された node の位置によって、他の node を移動させなくてはならないからです。
詳細は上の参考サイトやコードを見ていただきたいのですが、3つに場合分けされます。

削除する node が leaf の場合
- 対象の node を削除するだけ
削除する node が child node を1つもつ場合
- 対象の node があったところに child node を移動させる
削除する node が child node を2つもつ場合 (以下どちらでもよい)
- 削除する node の Right sub tree の最小値を root に移動させる
- 削除する node の Left sub tree の最大値を root に移動させる

func (t *Tree) DeleteNode(x Element) *Node {
	if t == nil {
		return nil
	}
	if t.root.data < x { // root が削除する対象の node ではない
		t.root.right = t.root.right.ChildTree().DeleteNode(x)
		return t.root
	} else if t.root.data > x { // root が削除する対象の node ではない
		t.root.left = t.root.left.ChildTree().DeleteNode(x)
		return t.root
	} else { // root が削除する対象の node である
		if IsLeaf(t.root) { // ① 削除する node が leaf (child node をもたない)のとき
			t.root = nil // 対象の node を削除するだけでよい
		} else if t.root.left == nil && t.root.right != nil { // ② 削除する node が child node を 1 つもつとき
			t.root = t.root.right // child node を root に移動させる
		} else if t.root.left != nil && t.root.right == nil { // ② 削除する node が child node を 1 つもつとき
			t.root = t.root.left // child node を root に移動させる
		} else { // ③ 削除する node が　child node を 2 つもつとき
			rightMin := t.RightSubTree(x).FindMostLeft().data // 削除する node の Right sub tree の最小値を root に移動させる
			t.root.data = rightMin
			t.root.right = t.root.right.ChildTree().DeleteNode(rightMin)
		}
		return t.root
	}
}

func (t *Tree) RightSubTree(x Element) *Tree {
	if t == nil {
		return nil
	}
	if t.root.data == x {
		return t.root.right.ChildTree()
	} else if t.root.data < x {
		return t.root.right.ChildTree().RightSubTree(x)
	} else {
		return t.root.left.ChildTree().RightSubTree(x)
	}
}

func (t *Tree) FindMostLeft() *Node {
	if t == nil {
		return nil
	}
	if t.root.left == nil {
		return t.root
	}
	return t.root.left.ChildTree().FindMostLeft()
}

以上をふまえて、Exerciseをやってみましょう。

💻 Exercise

1~9 がランダムに並んだ配列から Binary Search Tree を実装しましょう。
node の数を出力しましょう。
データが 2 の node を探索しましょう。
データが 2 の node を削除しましょう。
最後に全ての node を削除しましょう。

2~5を実行後に node を出力しておきましょう。
(次の Tree Traversal の内容になります。)

☟ 解答例

package main

import "fmt"

type TreeI interface {
	CountNodes() int
	PrintTree()
	Search(x Element) *Node
	InsertNode(x Element)
	DeleteNode(x Element) *Node
	RightSubTree(x Element) *Tree
	FindMostLeft() *Node
	DeleteAllNodes() *Node
}

type Element int

type Node struct {
	data  Element
	left  *Node
	right *Node
}

type Tree struct {
	root *Node
}

var _ TreeI = &Tree{}

func IsLeaf(node *Node) bool {
	if node == nil {
		return true
	}
	return node.left == nil && node.right == nil
}

func (n *Node) ChildTree() *Tree {
	if n == nil {
		return nil
	}
	return &Tree{root: n}
}

func (t *Tree) CountNodes() int {
	if t == nil || t.root == nil {
		return 0
	}
	if IsLeaf(t.root) {
		return 1
	}
	return 1 + t.root.left.ChildTree().CountNodes() + t.root.right.ChildTree().CountNodes()
}

func (t *Tree) PrintTree() {
	if t == nil || t.root == nil {
		fmt.Printf("nothing!")
		return
	}
	if t.root.left != nil {
		t.root.left.ChildTree().PrintTree()
	}
	fmt.Printf("%d ", t.root.data)
	if t.root.right != nil {
		t.root.right.ChildTree().PrintTree()
	}
}

func (t *Tree) Search(x Element) *Node {
	if t == nil {
		return nil
	}
	if t.root.data == x {
		return t.root
	}
	if t.root.data < x {
		return t.root.right.ChildTree().Search(x)
	} else {
		return t.root.left.ChildTree().Search(x)
	}
}

func (t *Tree) InsertNode(x Element) {
	node := &Node{data: x}
	if t.root == nil {
		t.root = node
	} else {
		if t.root.data < x {
			if rightChild := t.root.right.ChildTree(); rightChild != nil {
				rightChild.InsertNode(x)
			} else {
				t.root.right = node
			}
		} else {
			if leftChild := t.root.left.ChildTree(); leftChild != nil {
				leftChild.InsertNode(x)
			} else {
				t.root.left = node
			}
		}
	}
}

func (t *Tree) DeleteNode(x Element) *Node {
	if t == nil {
		return nil
	}
	if t.root.data < x {
		t.root.right = t.root.right.ChildTree().DeleteNode(x)
		return t.root
	} else if t.root.data > x {
		t.root.left = t.root.left.ChildTree().DeleteNode(x)
		return t.root
	} else {
		if IsLeaf(t.root) {
			t.root = nil
		} else if t.root.left == nil && t.root.right != nil {
			t.root = t.root.right
		} else if t.root.left != nil && t.root.right == nil {
			t.root = t.root.left
		} else {
			rightMin := t.RightSubTree(x).FindMostLeft().data
			t.root.data = rightMin
			t.root.right = t.root.right.ChildTree().DeleteNode(rightMin)
		}
		return t.root
	}
}

func (t *Tree) RightSubTree(x Element) *Tree {
	if t == nil {
		return nil
	}
	if t.root.data == x {
		return t.root.right.ChildTree()
	} else if t.root.data < x {
		return t.root.right.ChildTree().RightSubTree(x)
	} else {
		return t.root.left.ChildTree().RightSubTree(x)
	}
}

func (t *Tree) FindMostLeft() *Node {
	if t == nil {
		return nil
	}
	if t.root.left == nil {
		return t.root
	}
	return t.root.left.ChildTree().FindMostLeft()
}

func (t *Tree) DeleteAllNodes() *Node {
	if t != nil {
		t.root.left = t.root.left.ChildTree().DeleteAllNodes()
		t.root.right = t.root.right.ChildTree().DeleteAllNodes()
		t.root = nil
		return t.root
	}
	return nil
}

func main() {
	tree := &Tree{}
	integers := []Element{5, 2, 3, 8, 9, 1, 4, 6, 7}

	for _, v := range integers {
		tree.InsertNode(v)
	}

	fmt.Printf("count: %d\n", tree.CountNodes())
	tree.PrintTree()

	tree.DeleteNode(2)
	fmt.Printf("\nafter delete 2: ")
	tree.PrintTree()

	tree.DeleteAllNodes()
	fmt.Printf("\nafter delete all nodes: ")
	tree.PrintTree()
}

☟ 出力結果

count: 9
1 2 3 4 5 6 7 8 9 
after delete 2: 1 3 4 5 6 7 8 9 
after delete all nodes: nothing!

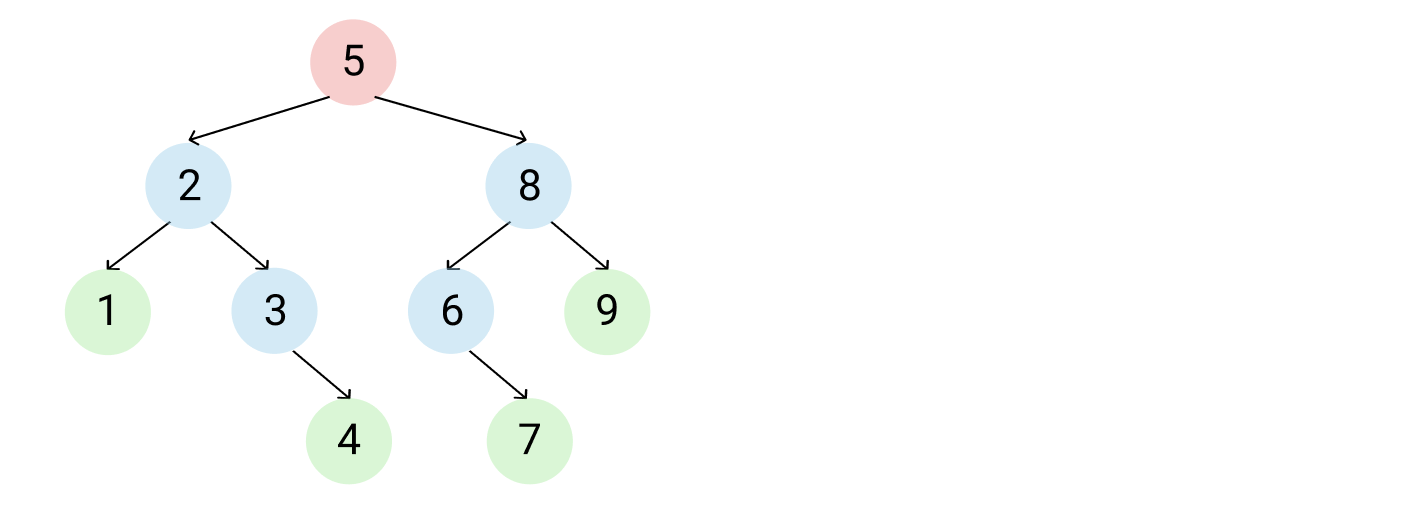
コードが長いので複雑に見えますが、出力結果の通り、Exerciseの前に記載したコードを組み合わせているだけです。

Tree Traversal

Tree にある全ての node を1回ずつ体系的に調査する処理のことです。
Traversal にはいくつか方法があります。

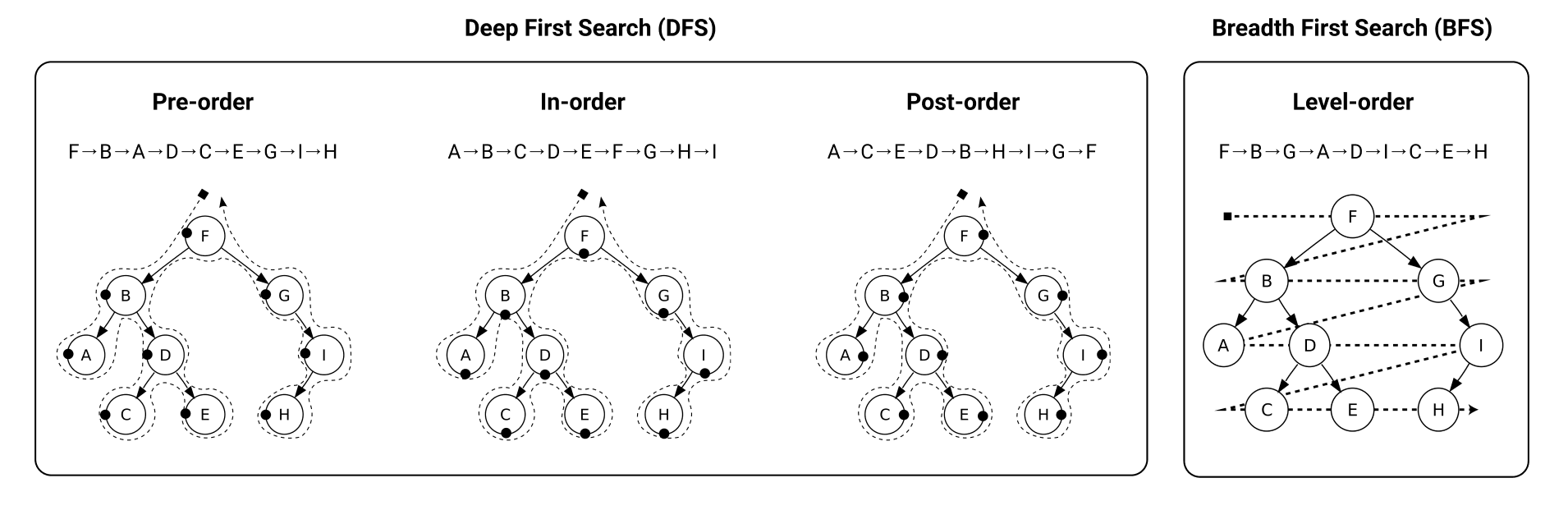
参考: Wikipedia 木構造 (データ構造)#走査法
以下の記事がわかりやすいです。

Deep First Search (DFS) は日本語では 深さ優先探索 と呼ばれます。
簡単にいうと、1つの node からいけるところまで探索していき、探索できなくなったらそこから一番近い点に戻って、再び探索をする走査法です。
In-order Traversal はソートされた順序になっているのでよく使われます。
※ データ構造としては Stack が使われますが、本記事では Recursive function で実装しています。

Breadth First Search (BFS) は日本語では 幅優先探索と呼ばれます。
探索を開始した地点から、深さが同じ node を浅い方から順番に探索をしていく走査法です。

各 Traversal を Go で実装すると以下のようになります。
DFS ではデータを出力しているタイミングが異なっていることが見てわかりますね。

Pre-order (前順 / 行きがけ順)

func (t *Tree) PreorderTraversal() {
	if t == nil || t.root == nil {
		fmt.Printf("nothing!")
		return
	}
	fmt.Printf("%s ", t.root.data)
	if t.root.left != nil {
		t.root.left.ChildTree().PreorderTraversal()
	}
	if t.root.right != nil {
		t.root.right.ChildTree().PreorderTraversal()
	}
}

In-order (間順 / 通りがけ順)

func (t *Tree) InorderTraversal() {
	if t == nil || t.root == nil {
		fmt.Printf("nothing!")
		return
	}
	if t.root.left != nil {
		t.root.left.ChildTree().InorderTraversal()
	}
	fmt.Printf("%s ", t.root.data)
	if t.root.right != nil {
		t.root.right.ChildTree().InorderTraversal()
	}
}

Post-order (後順 / 帰りがけ順)

func (t *Tree) PostorderTraversal() {
	if t == nil || t.root == nil {
		fmt.Printf("nothing!")
		return
	}
	if t.root.left != nil {
		t.root.left.ChildTree().PostorderTraversal()
	}
	if t.root.right != nil {
		t.root.right.ChildTree().PostorderTraversal()
	}
	fmt.Printf("%s ", t.root.data)
}

Level-order (レベル順)

func (t *Tree) LevelorderTraversal(queue []*Node) {
	if t == nil || t.root == nil {
		fmt.Printf("nothing!")
		return
	}

	if len(queue) == 0 {
		queue = append(queue, t.root)
		t.root.ChildTree().LevelorderTraversal(queue)
	} else {
		node := queue[0]
		queue = queue[1:]
		fmt.Printf("%s ", node.data)
		if node.left != nil {
			queue = append(queue, node.left)
		}
		if node.right != nil {
			queue = append(queue, node.right)
		}
		if len(queue) == 0 {
			return
		}
		queue[0].ChildTree().LevelorderTraversal(queue)
	}
}

Level-orderは他の Traversal と比較し、少しややこしいので流れを図にしました。

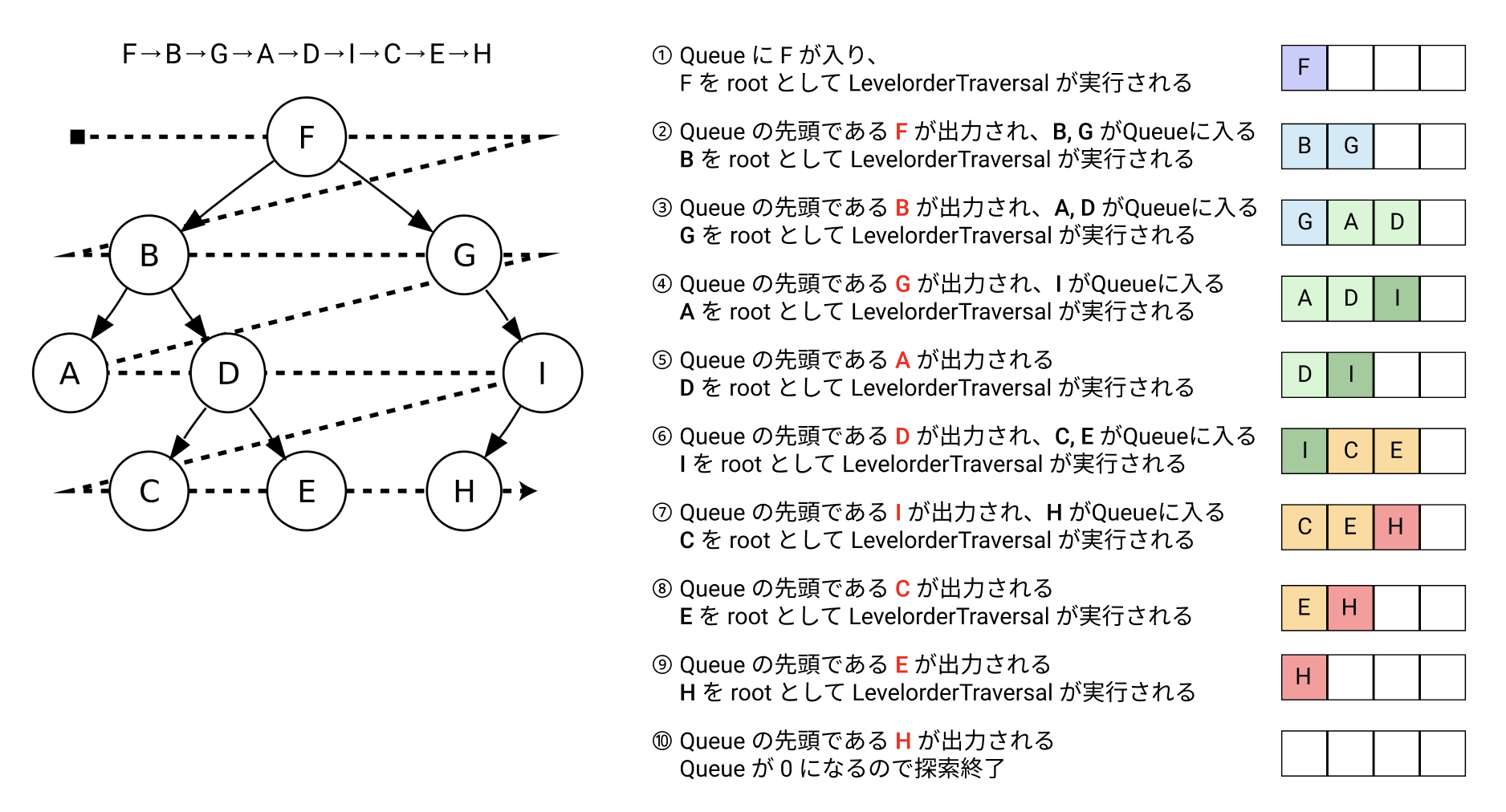
💻 Exercise

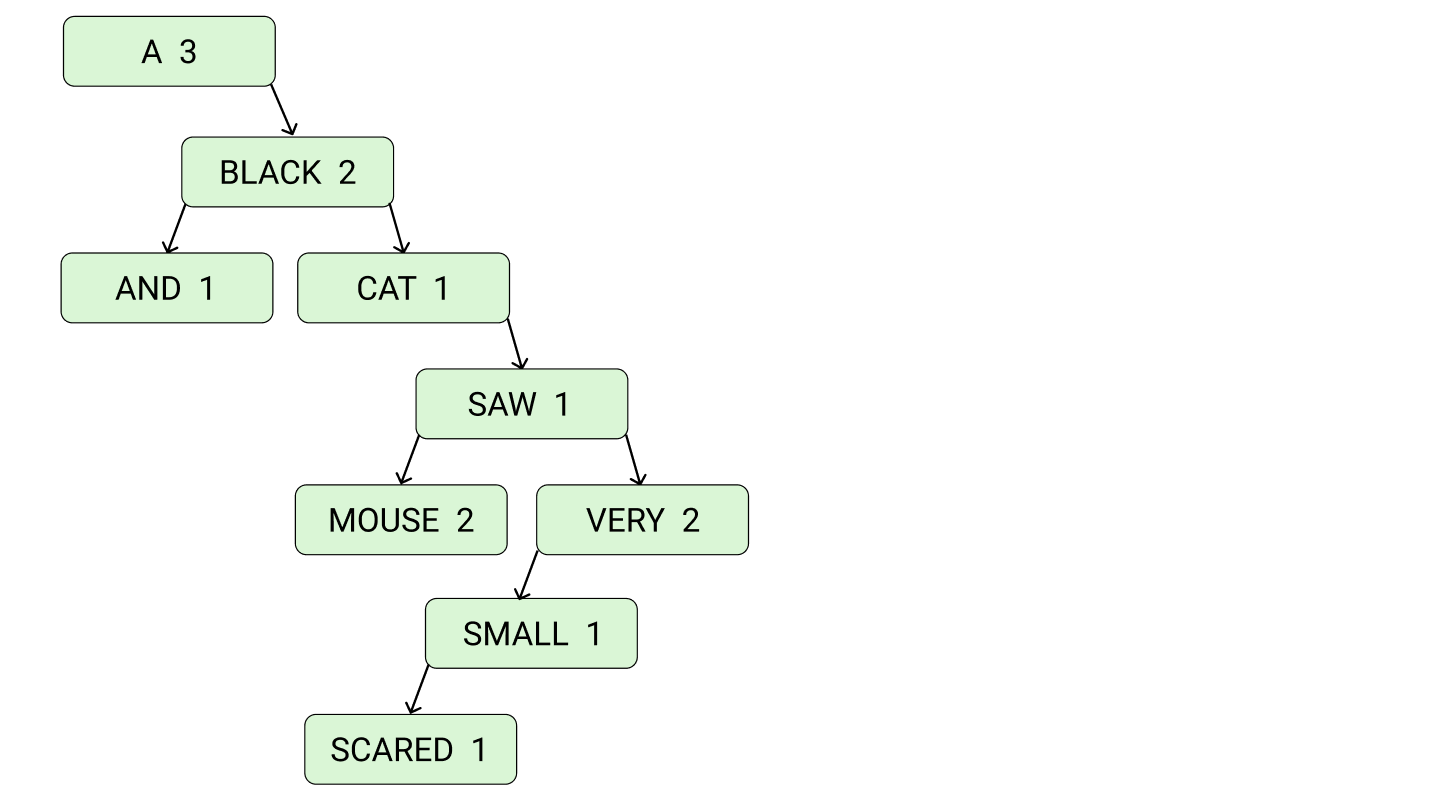
テキストファイルに入力されている文を読み取り、単語の出現頻度を出力するプログラムを実装しましょう。
☟ ファイル例

sentence.txt

A black black cat saw a very small mouse and a very scared mouse

☟ 出力例

A 3  AND 1  BLACK 2  CAT 1  MOUSE 2  SAW 1  SCARED 1  SMALL 1  VERY 2

☟ 解答例

package main

import (
	"bufio"
	"fmt"
	"io"
	"os"
	"strings"
)

type TreeI interface {
	WordCount(word string)
	PrintTree()
}

type Frequencies struct {
	word  string
	count int
}

type Node struct {
	data  *Frequencies
	left  *Node
	right *Node
}

type Tree struct {
	root *Node
}

var _ TreeI = &Tree{}

func (n *Node) ChildTree() *Tree {
	if n == nil {
		return nil
	}
	return &Tree{root: n}
}

// Tree を形成
func (t *Tree) WordCount(word string) {
	if t.root == nil {
		t.root = &Node{data: &Frequencies{word: word, count: 1}}
	} else {
		if t.root.data.word == word {
			t.root.data.count++
		} else if t.root.data.word < word {
			if rightChild := t.root.right.ChildTree(); rightChild != nil {
				rightChild.WordCount(word)
			} else {
				t.root.right = &Node{data: &Frequencies{word: word, count: 1}}
			}
		} else {
			if leftChild := t.root.left.ChildTree(); leftChild != nil {
				leftChild.WordCount(word)
			} else {
				t.root.left = &Node{data: &Frequencies{word: word, count: 1}}
			}
		}
	}
}

// In-order Traversal
// ソートされた順に単語と出現回数を出力する
func (t *Tree) PrintTree() {
	if t == nil || t.root == nil {
		fmt.Printf("nothing!")
		return
	}
	if t.root.left != nil {
		t.root.left.ChildTree().PrintTree()
	}
	fmt.Printf("%s %d  ", t.root.data.word, t.root.data.count)
	if t.root.right != nil {
		t.root.right.ChildTree().PrintTree()
	}
}

func check(e error) {
	if e != nil {
		if e != io.EOF {
			panic(e)
		}
	}
}

func main() {
	// ファイルから文を読み取って単語を抽出する
	f, err := os.Open("sentence.txt")
	check(err)

	defer f.Close()

	r := bufio.NewReader(f)
	sentence, err := r.ReadString('\n')
	check(err)

	sentence = strings.ToUpper(sentence)  // 読み取った文に含まれれるアルファベットを全て大文字にする
	words := strings.Split(sentence, " ") // 単語ごとに区切って Slice に格納する

	// 単語で Tree を形成する
	tree := &Tree{}
	for _, w := range words {
		tree.WordCount(w)
	}

	// Tree を出力
	tree.PrintTree()
}

☟ 出力結果

A 3  AND 1  BLACK 2  CAT 1  MOUSE 2  SAW 1  SCARED 1  SMALL 1  VERY 2

形成された Tree は下図のようになっています。

おわりに

Exerciseの解答例はあくまで例なので、もっといい書き方あるよ！という方、ぜひコメントをお寄せください！
説明についても、筆者自身が初心者であるため、ご指摘や補足は大歓迎でございます。

株式会社Link Sportsでは、あらゆるスポーツを楽しむ人たちに送る、チームマネジメントアプリを開発しています。
未経験でも経験豊富なエンジニアの方でも、スポーツ好きなら活躍できる環境があります！
絶賛エンジニア募集中です！
Wantedly ▶︎ https://www.wantedly.com/projects/324177
Green ▶︎ https://www.green-japan.com/job/82003

次回は、データ構造とアルゴリズム**#7 Sorting algorithms (ソートアルゴリズム)**です。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up