【Go】Sorting algorithms (ソートアルゴリズム)

Goでプログラミングの基礎を学ぶシリーズ

スクールでは教えてくれないプログラミングの基礎、データ構造とアルゴリズムをGoで学んでいくシリーズです。
そのデータ構造がどのようなものであるかは、理解を助けてくれるサイトを紹介しつつ、簡単な説明に留めさせていただきます。(ご自身でも調べてみてください！)
筆者自身、Exerciseに取り組みながら理解を深めていったので、コードの解説を中心に記事を書いていきたいと思います。

	タイトル
#0	はじめに (環境構築と勉強方法)
#1	Pointer, Array, String (ポインタと配列と文字列と)
#2	File operations (ファイル操作)
#3	Linked List (連結リスト)
#4	Stack & Queue (スタックとキュー)
#5	Search algorithms (探索アルゴリズム)
#6	Tree (木構造)
#7	Sorting algorithms (ソートアルゴリズム) ☜ here
#8	String pattern matching algorithms (文字列探索アルゴリズム)

今回は#7 Sorting algorithms (ソートアルゴリズム)です。

Sortとは

データを一定の規則に従って並び替えることです。
昇順や降順など日常生活でも馴染みがありますね。
Sort には多くのアルゴリズムが存在し、時間計算量が比較されます。
以下の記事はソートの様子が可視化されているので、直感的にわかりやすいと思います。

ここでは中でも代表的な Sort のアルゴリズムの Go での実装例をみていきます。
各ソートがどのような流れでソートしていくかは、上のサイトをご参考ください。

Insertion sort (挿入ソート)

リストのソート済みの部分に、新たな要素を適切な位置に挿入することを繰り返してソートを行うアルゴリズムです。
平均計算時間: $O(n^2)$ , 最悪計算時間: $O(n^2)$ と遅いのですが、アルゴリズムは単純で実装しやすいと思います。

func InsertionSort(numbers []int) []int {
    for i := 0; i < len(numbers); i++ {
        next := numbers[i] // ソートされていない部分の先頭

        fmt.Printf("next: %d\n", next)

        var j int
        // ソートされている部分で、 next が挿入されるところまで要素をずらしていく
        for j = i - 1; j >= 0 && next < numbers[j]; j-- {
            numbers[j+1] = numbers[j]

            fmt.Printf("j = %d, sorting... %v\n", j, numbers)
        }
        numbers[j+1] = next // next を挿入

        fmt.Printf("after insert next: %v\n\n", numbers)
    }
    return numbers
}

func main() {
    numbers := []int{7, 65, 8, 32, 4, 21, 10}
    InsertionSort(numbers)
}

所々にログを仕込んでみました。
ログを見ると、ソートの流れがよくわかるかと思います。

☟ 出力結果

next: 7
after insert next: [7 65 8 32 4 21 10]

next: 65
after insert next: [7 65 8 32 4 21 10]

next: 8
j = 1, sorting... [7 65 65 32 4 21 10]
after insert next: [7 8 65 32 4 21 10]

next: 32
j = 2, sorting... [7 8 65 65 4 21 10]
after insert next: [7 8 32 65 4 21 10]

next: 4
j = 3, sorting... [7 8 32 65 65 21 10]
j = 2, sorting... [7 8 32 32 65 21 10]
j = 1, sorting... [7 8 8 32 65 21 10]
j = 0, sorting... [7 7 8 32 65 21 10]
after insert next: [4 7 8 32 65 21 10]

next: 21
j = 4, sorting... [4 7 8 32 65 65 10]
j = 3, sorting... [4 7 8 32 32 65 10]
after insert next: [4 7 8 21 32 65 10]

next: 10
j = 5, sorting... [4 7 8 21 32 65 65]
j = 4, sorting... [4 7 8 21 32 32 65]
j = 3, sorting... [4 7 8 21 21 32 65]
after insert next: [4 7 8 10 21 32 65]

Selection sort (選択ソート)

リストのソートされていない部分から、最小値(or最大値)を持つ要素を探して、その値をソートされていない部分の先頭に移動(交換)することを繰り返してソートを行うアルゴリズムです。
平均計算時間: $O(n^2)$ , 最悪計算時間: $O(n^2)$ と遅いのですが、アルゴリズムは単純で実装しやすいと思います。

func SelectionSort(numbers []int) []int {
    for i := 0; i < len(numbers); i++ {
        min := i
        // ソートされていない部分での最小値の index を探す
        for j := i + 1; j < len(numbers); j++ {
            if numbers[min] > numbers[j] {
                min = j
            }
        }
        // ソートされていない部分の先頭と、ソートされていない部分での最小値を入れ替える
        numbers[i], numbers[min] = numbers[min], numbers[i]

        fmt.Printf("i = %d, %v\n", i, numbers)
    }
    return numbers
}

func main() {
    numbers := []int{7, 65, 8, 32, 4, 21, 10}
    SelectionSort(numbers)
}

☟ 出力結果

i = 0, [4 65 8 32 7 21 10]
i = 1, [4 7 8 32 65 21 10]
i = 2, [4 7 8 32 65 21 10]
i = 3, [4 7 8 10 65 21 32]
i = 4, [4 7 8 10 21 65 32]
i = 5, [4 7 8 10 21 32 65]
i = 6, [4 7 8 10 21 32 65]

Bubble sort (バブルソート)

隣り合う要素の大小を比較しながらソートしていくアルゴリズムです。
平均計算時間: $O(n^2)$ , 最悪計算時間: $O(n^2)$ と遅いのですが、アルゴリズムは単純で実装しやすいと思います。

func BubbleSort(numbers []int) []int {
    for i := 0; i < len(numbers)-1; i++ {
        for j := 0; j < len(numbers)-i-1; j++ {
            if numbers[j] > numbers[j+1] {
                numbers[j], numbers[j+1] = numbers[j+1], numbers[j]
            }
        }
        fmt.Printf("i = %d, %v\n", i, numbers)
    }
    return numbers
}

func main() {
    numbers := []int{7, 65, 8, 32, 4, 21, 10}
    BubbleSort(numbers)
}

☟ 出力結果

i = 0, [7 8 32 4 21 10 65]
i = 1, [7 8 4 21 10 32 65]
i = 2, [7 4 8 10 21 32 65]
i = 3, [4 7 8 10 21 32 65]
i = 4, [4 7 8 10 21 32 65]
i = 5, [4 7 8 10 21 32 65]

Heap sort (ヒープソート)

ヒープとは、データ構造の一種で、木構造（ツリー構造）のうち、親要素が子要素より常に大きい（あるいは小さい）という条件を満たすもの。
引用: IT用語辞典 e-Words

Heap sort は Binary Heap (二分ヒープ木) を用いて行うソートのアルゴリズムです。
ヒープの構造を利用するだけで、Tree を実装する必要はありません。
平均計算時間: $O(n\log{n})$ , 最悪計算時間: $O(n\log{n})$ であり、上の3つよりも速いソートアルゴリズムになります。

func HeapSort(numbers []int) []int {
    // heap を形成する
    fmt.Printf("Build Heap\n")
    for i := len(numbers)/2 - 1; i >= 0; i-- {
        heapify(numbers, len(numbers), i)
    }

    // heap から要素を一つずつ取り出す (ソートしていく)
    fmt.Printf("\nHeap Sort")
    for i := len(numbers) - 1; i > 0; i-- {
        numbers[i], numbers[0] = numbers[0], numbers[i]

        fmt.Printf("\ni = %d, sorting... %v\n", i, numbers)

        heapify(numbers, i, 0)
    }
    return numbers
}

// i 番目の要素を root とする Tree をヒープ化する.
// len は heap size, root は numbers の index
func heapify(numbers []int, len, root int) {
    largest := root // 最大の要素の index を i (root) としておく
    left := 2*root + 1
    right := 2*root + 2

    if left < len && numbers[left] > numbers[largest] { // left child が root より大きい場合
        largest = left
    }
    if right < len && numbers[right] > numbers[largest] { // right child が root より大きい場合
        largest = right
    }
    if largest != root { // 最大の要素が root ではないとき
        numbers[root], numbers[largest] = numbers[largest], numbers[root] // root の要素と最大の要素を入れ替える

        fmt.Printf("(%d %d %d) heapify... %v\n", root, left, right, numbers)

        heapify(numbers, len, largest)
    }
}

func main() {
    numbers := []int{7, 65, 8, 32, 4, 21, 10}
    HeapSort(numbers)
}

☟ 出力結果

Build Heap
(2 5 6) heapify... [7 65 21 32 4 8 10]
(0 1 2) heapify... [65 7 21 32 4 8 10]
(1 3 4) heapify... [65 32 21 7 4 8 10]

Heap Sort
i = 6, sorting... [10 32 21 7 4 8 65]
(0 1 2) heapify... [32 10 21 7 4 8 65]

i = 5, sorting... [8 10 21 7 4 32 65]
(0 1 2) heapify... [21 10 8 7 4 32 65]

i = 4, sorting... [4 10 8 7 21 32 65]
(0 1 2) heapify... [10 4 8 7 21 32 65]
(1 3 4) heapify... [10 7 8 4 21 32 65]

i = 3, sorting... [4 7 8 10 21 32 65]
(0 1 2) heapify... [8 7 4 10 21 32 65]

i = 2, sorting... [4 7 8 10 21 32 65]
(0 1 2) heapify... [7 4 8 10 21 32 65]

i = 1, sorting... [4 7 8 10 21 32 65]

流れを図にすると以下のようになります。

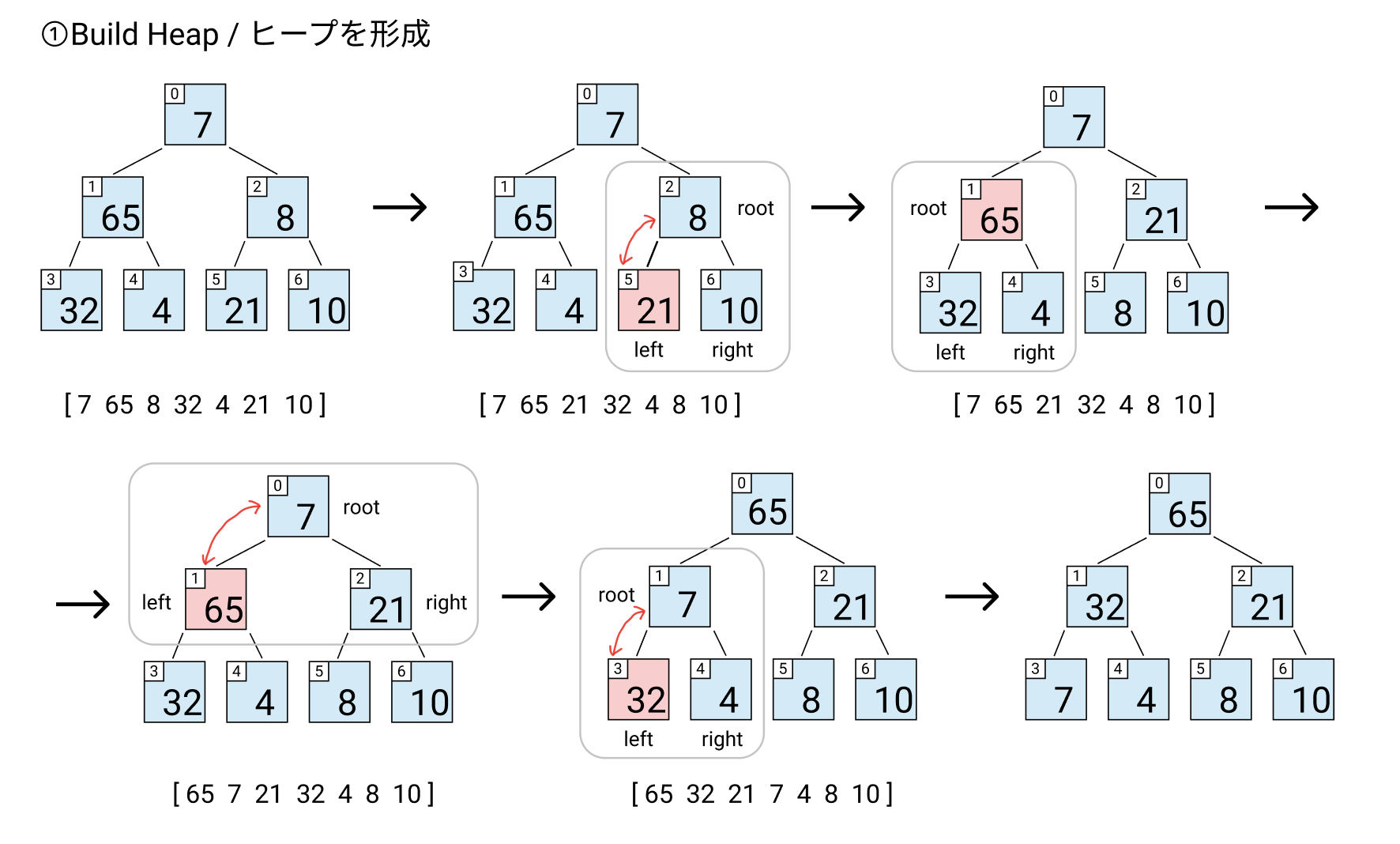
まずはランダムな配列のヒープ化を行います。
heapify　では root, left, right から最大の値を root と入れ替え、入れ替えが行われた index について再帰的に heapify を実行するという流れになります。

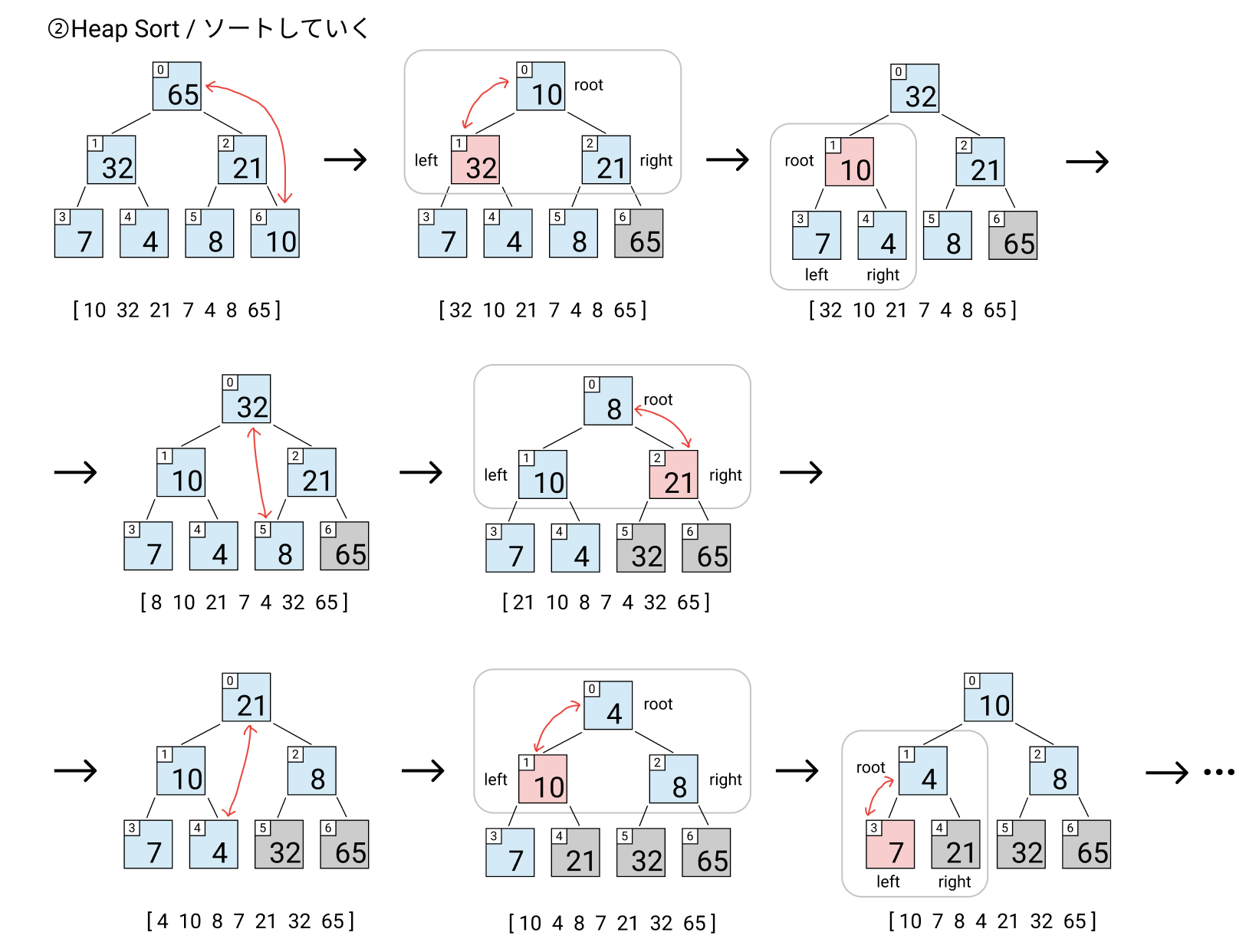
ヒープ化ができたらソートをしていきます。
ヒープ化により root が最大値になっているので、root と配列の最後尾を入れ替え、入れ替えが行われた後に再度ヒープ化( heapify )を実行します。
それの繰り返しにより、ソートされていきます。

Quick sort (クイックソート)

ピボットという基準となる値をランダムに選択し、リストの先頭からピボットよりも大きいか小さいかで両側のグループに分割し、それを繰り返してソートを行うアルゴリズムです。
平均計算時間: $O(n\log{n})$ , 最悪計算時間: $O(n^2)$ であり、Wikipediaによると、
他のソート法と比べて、一般的に最も高速だといわれているが対象のデータの並びやデータの数によっては必ずしも速いわけではない ようです。

func QuickSort(numbers []int) []int {
    if len(numbers) < 2 {
        return numbers
    }

    fmt.Printf("\nsorting... %v\n", numbers)

    left, right := 0, len(numbers)-1
    pivot := numbers[right]

    for i := 0; i < right; i++ {
        if numbers[i] < pivot {
            numbers[i], numbers[left] = numbers[left], numbers[i]
            left++

            fmt.Printf("p = %d, left = %d, %v\n", pivot, numbers[left], numbers)
        }
    }
    numbers[left], numbers[right] = numbers[right], numbers[left]

    fmt.Printf("p = %d, left = %d, %v\n", pivot, numbers[left], numbers)

    QuickSort(numbers[:left])
    QuickSort(numbers[left+1:])
    return numbers
}

func main() {
    numbers := []int{7, 65, 8, 32, 4, 21, 10}
    QuickSort(numbers)
}

☟ 出力結果

sorting... [7 65 8 32 4 21 10]
p = 10, left = 65, [7 65 8 32 4 21 10]
p = 10, left = 65, [7 8 65 32 4 21 10]
p = 10, left = 32, [7 8 4 32 65 21 10]
p = 10, left = 10, [7 8 4 10 65 21 32]

sorting... [7 8 4]
p = 4, left = 4, [4 8 7]

sorting... [8 7]
p = 7, left = 7, [7 8]

sorting... [65 21 32]
p = 32, left = 65, [21 65 32]
p = 32, left = 32, [21 32 65]

ソートの流れは最初にリンクした参考サイトの通りです。

Merge sort (マージソート)

ソートされていないリストを2つのリストに分割して、それぞれをソートした後、それらをマージしてソート済みのひとつのリストを作るアルゴリズムです。
平均計算時間: $O(n\log{n})$ , 最悪計算時間: $O(n\log{n})$

func MergeSort(numbers []int) []int {
    if len(numbers) < 2 {
        return numbers
    }
    middle := len(numbers) / 2
    return merge(MergeSort(numbers[:middle]), MergeSort(numbers[middle:]))
}

func merge(left, right []int) []int {
    var merged []int
    fmt.Printf("\nmerge %v %v\n", left, right)

    // 左のリストと右のリストの要素を比較し、小さい方を merged に追加する
    for i := 0; len(left) > 0 && len(right) > 0; i++ {
        if left[0] < right[0] {
            merged = append(merged, left[0])
            left = left[1:]
        } else {
            merged = append(merged, right[0])
            right = right[1:]
        }
        fmt.Printf("i = %d, %v\n", i, merged)
    }

    // リストに残っている要素を merged に追加
    for _, l := range left {
        merged = append(merged, l)
    }
    for _, r := range right {
        merged = append(merged, r)
    }

    fmt.Printf("sorted %v\n", merged)
    return merged
}

func main() {
    numbers := []int{7, 65, 8, 32, 4, 21, 10}
    MergeSort(numbers)
}

☟ 出力結果

merge [65] [8]
i = 0, [8]
sorted [8 65]

merge [7] [8 65]
i = 0, [7]
sorted [7 8 65]

merge [32] [4]
i = 0, [4]
sorted [4 32]

merge [21] [10]
i = 0, [10]
sorted [10 21]

merge [4 32] [10 21]
i = 0, [4]
i = 1, [4 10]
i = 2, [4 10 21]
sorted [4 10 21 32]

merge [7 8 65] [4 10 21 32]
i = 0, [4]
i = 1, [4 7]
i = 2, [4 7 8]
i = 3, [4 7 8 10]
i = 4, [4 7 8 10 21]
i = 5, [4 7 8 10 21 32]
sorted [4 7 8 10 21 32 65]

ソートの流れは最初にリンクした参考サイトの通りです。

💻 Exercise

1~500 の数字で構成される、要素数 500 のランダムな配列を Insertion sort と　Quick sort でソートしましょう。
その実行速度を比較してみましょう。

☟ 解答例

package main

import (
    "fmt"
    "math/rand"
    "time"
)

func initList(n int) []int {
    var numbers []int
    rand.Seed(time.Now().UnixNano())
    for i := 0; i < n; i++ {
        numbers = append(numbers, rand.Intn(500))
    }
    return numbers
}

func InsertionSort(numbers []int) []int {
    for i := 0; i < len(numbers); i++ {
        next := numbers[i]
        var j int
        for j = i - 1; j >= 0 && next < numbers[j]; j-- {
            numbers[j+1] = numbers[j]
        }
        numbers[j+1] = next
    }
    return numbers
}

func QuickSort(numbers []int) []int {
    if len(numbers) < 2 {
        return numbers
    }
    left, right := 0, len(numbers)-1
    pivot := numbers[right]

    for i := 0; i < right; i++ {
        if numbers[i] < pivot {
            numbers[i], numbers[left] = numbers[left], numbers[i]
            left++
        }
    }
    numbers[left], numbers[right] = numbers[right], numbers[left]

    QuickSort(numbers[:left])
    QuickSort(numbers[left+1:])
    return numbers
}

func main() {
    numbers := initList(500)
    start := time.Now()
    InsertionSort(numbers)
    runtime := time.Since(start)
    fmt.Printf("Insertion sort ▶︎ runtime: %v\n", runtime)

    numbers = initList(500)
    start = time.Now()
    QuickSort(numbers)
    runtime = time.Since(start)
    fmt.Printf("Quick sort ▶︎ runtime: %v\n", runtime)
}

☟ 出力結果

Insertion sort ▶︎ runtime: 44.611µs
Quick sort ▶︎ runtime: 23.602µs

おわりに

Exerciseの解答例はあくまで例なので、もっといい書き方あるよ！という方、ぜひコメントをお寄せください！
説明についても、筆者自身が初心者であるため、ご指摘や補足は大歓迎でございます。

株式会社Link Sportsでは、あらゆるスポーツを楽しむ人たちに送る、チームマネジメントアプリを開発しています。
未経験でも経験豊富なエンジニアの方でも、スポーツ好きなら活躍できる環境があります！
絶賛エンジニア募集中です！
Wantedly ▶︎ https://www.wantedly.com/projects/324177
Green ▶︎ https://www.green-japan.com/job/82003

次回は、データ構造とアルゴリズム#8 String pattern matching algorithms (文字列探索アルゴリズム)です。