深層ニューラルネットワークを用いたスケーラブルなベイジアン最適化

ニューラルネットの最適化について勉強中です。
ベイジアン最適化(BO)でのハイパーパラメータ最適化は昔からあったが時間がかかった。
そこでニューラルネットでベイジアン最適化を模倣することで並列化をしスピードアップに試みた。と解釈。
かなりの斜め読みなのでまたちゃんと読む。

このリポジトリには、James BrofosとRui Shuによって作成されたPythonコードが含まれています。このアプローチは、最適化技術の基礎となるニューラルネットワークを継続的に再学習し、スピード性能を向上させるための並列化設定でこの手法を実装します。
だと。
そもそもハイパーパラメータの最適化を自動化するのは普通やろ。
今はスピードにこだわってるぜって言ってはる。

ソースはこっち
https://github.com/RuiShu/Neural-Net-Bayesian-Optimization

#フォルダ構成

.
├──data
├──learning_objective
│   ├── gaussian_mix.py
│   ├── gaussian_process.py
│   ├── hartmann.py	
│   └── hidden_function.py
├──mpi
│   ├── mpi_definitions.py
│   ├── mpi_master.py
│   ├── mpi_optimizer.py
│   ├── mpi_trainer.py
│   ├── mpi_worker.py
│   └── theano_definitions.py
├──sequential
│   ├── seq_gaussian_process.py
│   ├── seq_optimizer.py
│   └── test.py
└──utilities
    ├── linear_regressor.py
    ├── neural_net.py
    └── optimizer.py

#コード実行

4つのコアと並行してホームディレクトリからコードを実行するには、単にmpiexecを呼び出します。

mpiexec -np 4 python -m mpi.mpi_optimizer

コードの連続したバージョンを実行するには：

python -m sequential.seq_optimizer

ベイジアン最適化のガウスプロセスバージョンを実行するには：

python -m sequential.seq_gaussian_process

サンプル出力：

Randomly query a set of initial points...  Complete initial dataset acquired
Performing optimization... 
0.100 completion...
0.200 completion...
0.300 completion...
0.400 completion...
0.500 completion...
0.600 completion...
0.700 completion...
0.800 completion...
0.900 completion...
1.000 completion...
Sequential gp optimization task complete.
Best evaluated point is:
[-0.31226245  3.80792522]
Predicted best point is:
[-0.31226245  3.7755048 ]

注：このコードは、書かれているように、ブラックボックス機能にアルゴリズムの使用を集中しています。 learning_objectiveには、いくつかの一般的な関数があります。選択された関数はhidden_​​function.pyで設定されます。並列化されたコードによって得られる時間節約を本当に理解するためには、現実のブラックボックス関数を評価する（すなわち、所与のハイパーパラメータのセットでMLアルゴリズムのテスト性能を計算する）には時間がかかることを認識することが重要である。 これは、hidden_​​function.pyの＃time.sleep（2）という行のコメントを外すことでシミュレートできます。

下記は論文。なんとなくわからないとバグもわからないので、一応見た。

---

#動機
ほとんどの機械学習アルゴリズムの成功は、ハイパーパラメータの適切な調整に依存する。ハイパーパラメータチューニングの一般的な手法はベイジアン最適化であり、ガウスプロセスを使用して超過パラメータ空間を補間する。しかし、GPベースのベイジアン最適化の計算時間は、サンプルサイズ（テストされたハイパーパラメータの数）に対して急速に増加し、すべてが同時に難しくない場合は、非常に時間がかかります。幸いにも、ニューラルネットワークは、Guassianプロセスの振る舞いを模倣することができますが、計算時間を大幅に短縮します。

#抜粋
ベイジアン最適化は、高価な評価を伴う関数の大域的最適化のための有効な方法論である。
これは、比較的安価な代理モデルによって定義された関数に対する分布を照会することに依存する。
関数に対するこの分布の正確なモデルは、アプローチの有効性にとって非常に重要であり、一般的にガウスプロセス（GP）を使用してフィットします。
しかし、GPは観測数に応じて3次元にスケーリングされるため、最適化が多くの評価を必要とする目的を処理することは困難であり、最適化を大規模に並列化することも困難です。
この研究では、関数に対する分布をモデル化するために、GPの代わりにニューラルネットワークの使用法を探っています。
パラメトリック・フォームとしてのニューラル・ネットワークによる適応基底関数回帰を実行すると、最先端のGPベースのアプローチと競合して実行されますが、3次元ではなくデータ数に比例して直線的に拡大することがわかります。これにより、従来の困難な並列度を達成することができました。
大規模なハイパーパラメータの最適化、畳み込みネットワークを使用したベンチマークオブジェクト認識タスクの競合モデルの発見、神経言語モデルを使用した画像キャプションの生成。

1. はじめに

最近、機械学習の分野では、豊富なデータ、計算能力の向上、新しいアルゴリズム、多数のエキサイティングな新しいアプリケーションのために、前例のない成長が見られました。
研究者がより悲惨な問題に取り組むにつれ、彼らが使用するモデルもより洗練されたものになります。
しかし、機械学習モデルの複雑化に伴い、必然的に追加のハイパーパラメータが導入されます。これらは、ニューラルネットワークアーキテクチャの形状、学習率などの最適化パラメータ、重量除算などの正則化超過パラメータなどの設計上の決定から、これらのハイパーパラメータの適切な設定は、困難な問題のパフォーマンスにとって重要です。
ハイパーパラメータの設定を、グリッドやランダム探索（Bergstra＆Bengio、2012）などの単純な手順から、ランダムフォレストを使用したより洗練されたモデルベースのアプローチに至るまで最適化する方法は多数あります（Hutter et al。、2011 ）またはガウス過程（Snoek et al。、2012）である。ベイジアン最適化は、騒々しい高価なブラックボックス関数のモデルベースのグローバル最適化のための自然なフレームワークです。不確実性をモデリングするための原則的なアプローチを提供し、探索中に探査と利用を自然に均衡させることができます。ベイジアン最適化で最も一般的に使用されるモデルは、コンディショニングと推論の点でシンプルさと柔軟性があるため、ガウスプロセス（GP）です。
しかし、GPベースのベイジアン最適化の主な欠点は、密度の高い共分散行列を逆転させる必要があるため、推論時間が観測数の3倍になることです。

非常に少数のハイパーパラメータの問題については、これは問題ではありません。なぜなら、立方体スケーリングがさらなる評価を不可能にする前に、最小値がしばしば発見されるからです。
しかし、機械学習モデルの複雑さが増大するにつれて、十分な品質の解が見つかる前に評価される必要のある超過パラメータ構成の数とともに、探索空間のサイズもまた増大する。幸運なことに、モデルの複雑さが増すにつれて、計算がかなり容易になり、多数のモデルを並行して訓練することが可能になりました。したがって、ハイパーパラメータ探索問題の自然な解は、スケーラブルなベイジアン最適化法と大規模並列性を結合することです。しかしながら、GPの3次スケーリングは、このアプローチを追求することを実行不可能にしている。

この作業の目的は、ベイジアン最適化をスケーリングする方法を開発することですが、依然として望ましい柔軟性と不確実性の特性を維持しています。そのために、ベイジアン線形回帰の基礎関数の適応集合を学習するためのニューラルネットワークの使用を提案する。我々は、グローバル最適化のためのディープ・ネットワーク（DNGO）というこのアプローチに注目します。標準的なガウスプロセスとは異なり、DNGOは、ハイパーパラメータの最適化の場合、訓練されたモデルの数に対応する関数評価の数に比例して直線的に拡大し、確率的勾配トレーニングに適しています。調整しているモデルのハイパーパラメータをチューナ自体に設定する問題を単に動かしているように見えるかもしれませんが、適切な設計選択肢のセットでは、多くの大域的な最適化問題で一般化する効果的なベイジアン最適化システムです。

我々は、ベイジアン最適化のベンチマーク問題、物体認識のための畳み込みニューラルネットワーク、および画像キャプション生成のためのマルチモーダル神経言語モデルを含む多くの困難な問題に対するDNGOの有効性を実証する。 CIFAR-10とCIFAR-100でそれぞれ6.37％と27.4％の最先端の結果と競合するハイパーパラメータ設定があり、Microsoft COCO 2014データセットのBLEUスコアは25.1と26.7です1つのモデルと3つのモデルのアンサンブル。

2. 背景と関連仕事

2.1 ベイジアン最適化

ベイジアン最適化は、雑音の多い高価なブラックボックス関数をグローバルに最適化するための確立された戦略です（Mockus et al。、1978）。詳細なレビューについては、Lizotte（2008）、Brochu et al。 （2010）およびOsborne et al。 （2009）。ベイジアン最適化は、入力空間から目的の目的への目的関数に対する分布を定義する確率論的モデルの構築に依存する。

関数形式上の事前の条件と入力 - ターゲット対

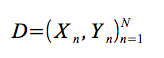
のN個の観測の条件に条件付けされた場合、関心のある高価な関数の最適値をどこで探すべきかを推論するために、比較的安価な事後関数が照会される。
新しい実験の約束は、後方平均と分散に適用された取得関数(acquisition function)を用いて定量化され、探査と開発？（exploitation）の間のトレードオフを表す。ベイズ最適化は、次の入力を評価するために、この取得関数に対してプロキシ最適化を実行することによって行われます。

最近のイノベーションは、洗練された理論的結果（Srinivas et al。、2010; Bull、2011; de Freitas et al。、2012）、マルチタスクおよび転送最適化（Krause＆Ong、2011; Swersky et al。、2013; Bardenet et al。、2013）、センサセット選択（Garnett et al。、2010）、適応モンテカルロ（Mahendran et al。、2012）のチューニング、ロボット歩行制御（Ca- landra et al。、2014b）。
一般的に、GPは柔軟性、較正された不確実性、解析的特性のためにベイジアン最適化で使用される関数の分布を構築するために使用されてきた（Jones、2001; Osborne et al。、2009）。最近の研究では、高次元の問題（Wang et al。、2013; Djolonga et al。、2013）、非定常性の入力（Snoek et al。、2014）、およびメタ学習による初期化（Feurer et al。、2015）。データと線形に比例するランダムな森林もまた、Hutterらによるアルゴリズム構成では成功裏に使用されている。 （2011年）にモデル不確実性の実証的推定値を示す。

より具体的には、ベイジアン最適化は、Xを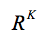のコンパクトなサブセットにする最小化問題

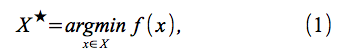
を解くことを試みる。

我々の作業では、GP代理と予期された改善獲得機能を使用するJones（2001）の標準的なGPベースのアプローチを構築する（Mockus et al。、1978）。

代理モデルの超過パラメータ

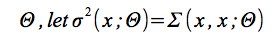
は、確率モデルの限界予測変数であり、

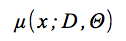
は予測平均であり、

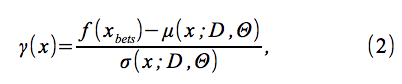
を定義する。ここで、f（xbest）は最小観測値である。

期待される改善基準は、以下のように定義される。

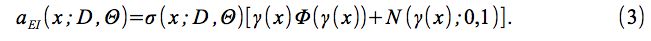
である。ここでΦ（・）は標準法線の累積分布関数であり、N（・; 0,1）は標準法線の密度。
我々のアプローチの分析特性に影響を与えることなく使用することができる、数多くの代替取得関数およびそれらの組み合わせが提案されている（Kushner、1964; Srinivasら、2010; Hoffmanら、2011）。

2.2 ベイジアンニューラルネットワーク

ベイジアン法をニューラルネットワークに適用すると、機械学習に豊富な歴史があります（MacKay、1992; Hinton＆van Camp、1993; Buntine＆Weigend、1991; Neal、1995; De Freitas、2003）。ベイジアンニューラルネットワークの目的は、不確実性を捕捉し、正則化者として行動し、モデル比較の枠組みを提供するために、ネットワーク重みの全事後分布を明らかにすることである。しかし、大部分のニューラルネットワークでは完全な事後確率は扱いにくく、高価な近似推論やマルコフ連鎖モンテカルロシミュレーションを必要とする。
より最近では、全体的なアーキテクチャの小さな部分について、完全または近似のベイジアン推論が検討されています。例えば、この研究と同様の精神で、La zaro-Gredilla＆Figueiras-Vidal（2010）; Hinton＆Salakhutdinov（2008）およびCalandra et al。 （2014a）は、ニューラルネットワークのちょうど最後の層に対する推論を考慮した。あるいは、Kingma＆Welling（2014）で変分アプローチが開発されている。 Rezende et al。 （2014）およびMnih＆Gregor（2014）に記載されている。ここで、ニューラルネットワークは、ディレクティブ生成ニューラルネットワークの潜在変数にわたる事後分布に対する変分近似で使用される。

3. ディープニューラルネットワークを用いた適応基底回帰

GPベースのベイジアン最適化の重要な制限は、この技術の計算コストが観測数の3乗に比例し、最適化するために観測数が比較的少ない目的へのアプローチの適用性が制限されることです。
この作業では、ベイズ最適化で伝統的に使用されていたGPを、それほど劇的ではないモデルに置き換えることを目標にしていますが、柔軟性や較正された不確かさなどのGPの望ましい特性のほとんどを保持します。ベイジアン・ニューラル・ネットワークは、ガウス過程と無限ベイズ・ニューラル・ネットワークとの理論的関係のために（Neal、1995; Williams、1996）、自然な考慮事項である。しかし、これらを大規模に展開するには、計算コストが非常に高くなります。
このように、我々は実用的なアプローチを取って、深層ニューラルネットワークの最後の隠れ層にベイジアン線形回帰を加え、残りのパラメータについての点推定を使用しながらネットの出力重みのみを抹消する。
これは適応基底回帰をもたらし、確立された観測数が直線的に変化する統計的手法であり、基底関数の次元性では3次的に変化する。これにより、評価時間とモデル能力を明確にトレードオフすることができます。このように、我々はニューラルネットワークによって定義された非常に柔軟で強力な非線形関数を用いて基礎を形成する。

まず、一般性を失うことなく、各入力ディメンションに対する補完的サポートを仮定して、入力空間を単位超立方体にスケーリングする。

我々は入力とターゲット

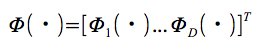
で訓練されたネットワークの最後の隠れ層からの出力のベクトルを

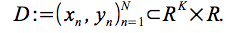
で表す。
私たちは、これらを基本機能のセットとみなしています。

さらに、Φをデータとこの基底から生じる設計行列とする。ここで、

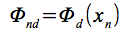
は出力設計行列、yは積み重ねられた目標ベクトルである。

これらの基底関数は、ディープニューラルネットワークの重みとバイアスによってパラメータ化され、これらのパラメータは、逆伝播と勢いでの確率的勾配降下によって訓練される。このトレーニング段階では、線形出力層も適合する。
この手順は、ネットワーク内のすべてのパラメータの最大事後（MAP）推定として見ることができる。この「基底関数ニューラルネットワーク」が訓練されると、MAPパラメータ化された出力層を、重みの不確実性を捕らえるベイジアン線形回帰器で置き換えます。この選択肢の説明は、3.1.2節を参照してください。

モデルの予測平均μ（x;Θ）および分散σ2（x;Θ）は、


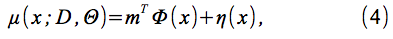
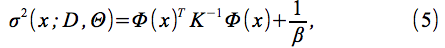
の

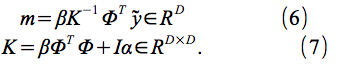
によって与えられる。ここで、η（x）は、3.1.3節および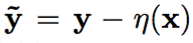に記載された事前平均関数である。

さらに、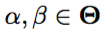は回帰モデルのハイパーパラメータである。 Snoek et al。の方法論に従ってスライスサンプリング（Neal、2000）を用いてαとβを統合する。 （2012年）

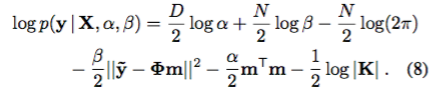
によって与えられた限界尤度以上では、この手順の計算上のボトルネックはKの逆数であることは明らかである。

しかし、この行列のサイズは、GPの場合のように観測数Nではなく、出力次元数Dで大きくなることに注意してください。これにより、図1に示されているように、GPよりもかなり多くの観測値にスケールアップすることができます。

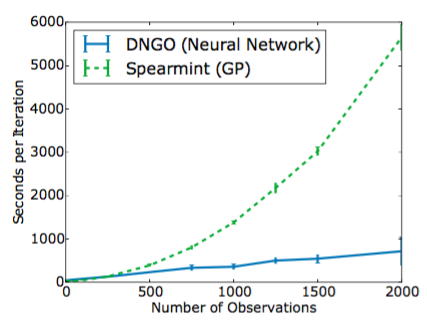
図1. Snoekらによる最先端のGPベースの手法と比較した本発明者らの方法の提案された実験当たりの時間。 （2014年）を6次元ハルトマン関数に適用する。各アルゴリズムを同じ32コアシステムで80GBのRAMで5回実行し、平均と標準偏差をプロットしました。

3.1 モデルの詳細

3.1.1 ネットワークアーキテクチャ

深いネットワークを使用することに対する自然の懸念は、特定の問題を調整して調整するために多大な努力を必要とすることが多いことです。アーキテクチャを調整し、ニューラルネットワークのハイパーパラメータをそれ自体が困難なハイパーパラメータ最適化問題として調整することを考慮することができる。もう一つの課題は、最適化の問題を横断して一般化するアプローチを作成することです。

我々は、使用される活性化関数のタイプなどの設計上の決定が、ベイジアン最適化ルーチンの性能を大幅に変更することを発見した。たとえば、図2では、一般的に使用される整流線形（ReLU）関数は不確実性の推定値が非常に低いため、ベイジアン最適化ルーチンを過度に探索する可能性があります。有界なtanh関数は現実的な分散を伴う滑らかな関数になるので、この作業ではこの非線形性を使用します。しかし、滑らかさの仮定を緩和する必要がある場合、基底を束縛するために最後の層でのみtanh関数を有する整流された線形関数の組み合わせを使用することもできる。
隠れ層の幅や規則化の量など、残りのハイパーパラメータを調整するために、GPベースのベイジアン最適化を使用しました。 1〜4層ごとにベイジアン最適化を実行しました。
Spearmint（Snoek et al。、2014）パッケージを使用して、一連のベンチマークグローバルオプティマイゼーションの問題の平均相対損失を最小限に抑えます。我々は、各レイヤーのウェイトとドロップアウトレート（Hinton et al。、2012）のセットごとにグローバル学習率、モーメントム、レイヤーサイズ、正規化ペナルティを調整した。

興味深いことに、最適な設定ではドロップアウトはなく、非常に適度な12正規化を特長としていました。おおよその補正項があるにもかかわらず、ドロップアウトが予測平均値にノイズを発生させ、結果として精度が低下すると考えられます。オプティマイザは代わりに、少数の隠れたユニットを介して容量を制限することを推奨しました。すなわち、最適なアーキテクチャは、3つの隠れ層と1層あたり約50の隠れた単位を持つ深くて狭いネットワークです。我々は経験的評価を通して同じアーキテクチャを使用し、このアーキテクチャを図2（d）に示します。

3.1.2 マジカル・ライクリッジVS地図推定

適応型ベーシスの回帰に対する標準的な経験的ベイズのアプローチは、ベーシスのパラメータ（式8を参照）に対する限界尤度を最大にすることであり、モデルの不確実性を考慮する。しかし、本手法の文脈では、確率勾配の各更新時にD×D行列を反転する必要がある周辺尤度の勾配を評価する必要がある。これにより、ネットの最適化が大幅に遅くなるため、現実的なアプローチをとり、ポイント推定値を使用して基礎を最適化し、ベイズ線形回帰層を事後的に適用します。両方のアプローチで質的にも経験的にも同様の結果が得られ、実際にはより効率的なものを採用しています。

3.1.3 四次元

ベイジアン最適化の利点の1つは、目的関数と探索空間に関する事前情報を組み込むための自然な手段を提供することです。例えば、探索空間の境界を選択するとき、典型的な仮定は、最適解が入力空間の内部のどこかにあることです。しかし、次元の呪いによって、空間の大半はその境界に非常に近いところにある。

したがって、境界探索領域を中心とする凸二次関数、すなわちcが中心である

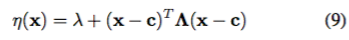
で粗く近似されているという我々の従属する先の信念を反映するために、平均関数η（x）（式4参照）を選択するλはオフセットであり、Λは対角スケーリング行列である。

我々は、対角要素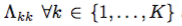上のc、horseshoe（Carvalho et al。、2009）のプリオーターに平均0.5（単位超立方体の中心）のガウス関数を前置し、周縁尤度をスライスサンプリングしてb、λ、cを積分する。

horseshoeは、希薄性を誘導するためのいわゆる1群前のものであり、回帰モデルの重みのための幾分珍しい選択である。これは、1）正の実数のみをサポートして凸関数につながり、2）裾が太くゼロに大きなスパイクを持ち、小さい値の場合には収縮が大きくなり、大きなものを取り入れる。この最後の効果は、2次効果が消えて必要に応じて簡単なオフセットになるため、モデルの誤特定を処理する上で重要です。

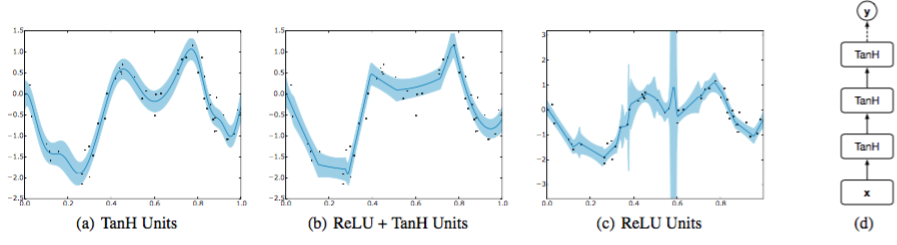
図2（a）のみのtanh、2（c）のみの整流線形（ReLU）活性化関数、または2（b）ReLUを使用したときのモデルによって学習された予測平均と不確かさの比較、最後の隠れた層のtanh 。斜線で示した領域は、平均値周辺の標準偏差エンベロープに対応する。活性化関数の選択は、モデルによって学習された基底関数を大幅に変更する。深いニューラルネットワークの標準であるReLUは非常に柔軟性がありますが、無限の活性化が非常に大きな不確かさの推定につながる可能性があることがわかりました。図2（d）は、DNGOモデルの全体的なアーキテクチャを示しています。破線は、疎外された重みに対応する。

3.2 入力スペースの制約を組み込む

関心のある多くの問題は複雑で、おそらくは未知の境界を持っているか、入力空間の一部の領域で未定義の動作を示しています。これらの領域は、探索空間上の制約として特徴付けることができる。
近年の研究（Gelbart et al。、2014; Snoek、2013; Gramacy＆Lee、2010）で制約分類器を学習し、制約違反の確率で期待される改善を割り引くことにより、GPベースのベイジアン最適化における未知の制約をモデル化する手法を開発した。

より具体的には、cn∈{0,1}を入力xnの妥当性のバイナリインジケータと定義する。また、有効入力と無効入力の組をV = {（xn、yn）| cn = 1}であり、I = {（xn、yn）| cn = 0}となる。 D：= V∪Iであることに留意されたい。最後に、Ψを制約ハイパーパラメータの集合とする。

修正された期待される改善関数は、

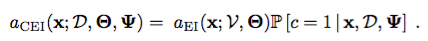
として書くことができる。
この作業では、拘束曲面をモデル化するために、出力層の重みを統合して、ガウス過程を適応基礎モデルに置き換えます。

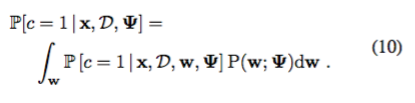
この場合、私たちはpos-teriorにLaplace近似を使用します。

ノイズの多い拘束に対しては、P [c = 1 | 2]のロジスティック尤度関数を使用してベイジアン反復回帰を実行します。 x、D、w、Ψ]である。ノイズのない制約に対しては、ロジスティック関数をステップ関数に置き換えます。

3.3 並列ベイジアン最適化

複数の入力にまたがる共同買収機能のクローズド・フォーム表現を得ることは、一般的に難しい（Ginsbourger＆Riche、2010）。しかし、ベイジアン最適化を並列化するMonte Carlo戦略が成功したのは、Snoek et al。 （2012）。この考えは、新しい実験についての決定を下す際に、現在実行中の実験の可能な結果を​​疎遠にすることである。この戦略に従うと、式4と式5によって与えられる先の予測分布を使用して、実行中の実験ごとに一連の幻想の結果を生成し、それを使って既存のデータセットを補強します。ファンタジーセットを平均化することで、候補点のEIを計算する際に、周縁化を近似することができます。この同じアイデアは、制約ネットワークに作用することに注意してください。制約ネットワークでは、周辺EIを計算する代わりに、制約に違反する可能性がある周縁化された確率を計算します。

そのためには、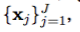で現在実行中のジョブがあれば、周辺獲得関数

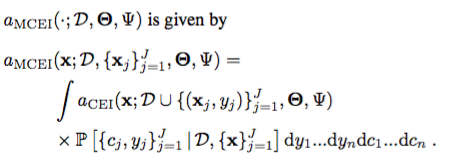
この戦略をGPに適用すると、候補点のEIを計算するコストは、拡張されたデータセットこれは、許容できるランニング実験の回数と、疎外化に使用されるファンタジーセットの数の両方を制限する。 DNGOを使用すると、より高度な並列性に対応するために、これらの両方をスケールアップすることが可能です。

最後に、Snoek et al。 （2012）では、モデルのハイパーパラメータを統合して、最終的な統合取得関数を取得しています。

最適化ルーチンの反復ごとに、次の入力x *を選択して、

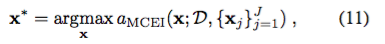
に従って

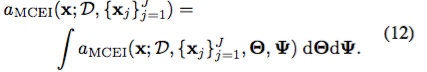
の評価します。

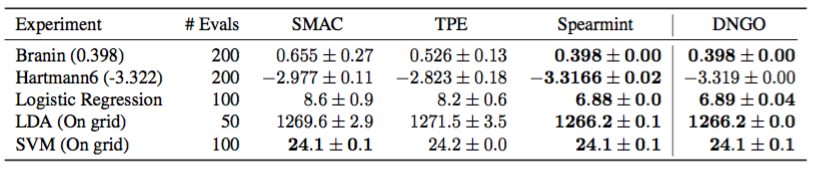
表1.グローバル最適化ベンチマーク問題対スケーラブル（TPE、SMAC）およびスケーラブル（スペアミント）ベイジアン最適化手法に対するDNGOの評価すべての問題は最小化の問題です。問題ごとに、各方法を10回実行してエラーバーを作成しました。

4.実験

4.1 HPOLibベンチマーク

文献には、モデルに基づく最適化のためのいくつかの他の方法が存在する。これらの中で、機械学習における最も一般的な変形は、ランダムな森林ベースのSMAC手順（Hutter et al。、2011）と木のParzen推定子（TPE）である（Bergstra et al。、2011）。これらは、ガウスプロセスよりも速くフィットし、大規模なデータセットではよりうまくスケールされますが、これは不確実性を発見的に処理する代償です。対照的に、DNGOは、スケーラビリティとモデルパラメータとハイパーパラメータのベイジアン周縁化との間のバランスを提供します。

我々のアプローチの有効性を実証するために、Snoekらの入力反りガウスプロセス法と同様に、これらのスケーラブルなモデルベースの最適化バリアントとDNGOを比較する。 HPOLibパッケージ（Eggensperger et al。、2013）の継続的な問題のベンチマークセットについては、表1に示すように、DNGOはSMACとTPEを大きく上回り、ガウスプロセスアプローチと競合しています。これは、スケーラビリティが大幅に向上したにもかかわらず、DNGOはガウスプロセス法の統計効率を最小値を求めるために必要な評価数の点で保持していることを示しています。

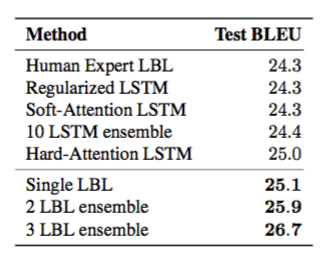
表2 Microsoft COCO 2014テストセットでBLEU-4を使用した画像キャプション生成結果正規化され集められたLSTMの結果はZaremba et al。 （2015）。人間の専門家によって調整されたベースラインのLBLおよびSoft and Hard Attentionモデルは、Xu et al。 （2015）。最適化によって得られたトップモデルのアンサンブルは結果を大幅に改善します。我々は、ハイパーパラメータ空間において明確な複数の局所的最適化が存在することに気づいた。これは、モデルの小さなサブセットを集合させることによる劇的な改善を説明することができる。

4.2 画像キャプションの生成

この実験では、合理的な時間内に進歩させるために非常にパラレルな評価が必要な実用的で高価な問題にDNGOの有効性を調査します。我々は、マルチモーダル神経言語モデルを用いて画像キャプチャ生成のタスクを検討する。具体的には、Kirosらの対数線形モデル（LBL）の超過パラメータを最適化します。最近リリースされたCOCOデータセット（Lin et al。、2014）からの検証セットのBLEUスコアを最大化するために、我々の実験では、このモデルの各評価は平均26.6時間かかった。

図3. COCO 2014データセットのベストLBLモデルからのサンプル画像とキャプションのサンプル。最初の2つのキャプションはそれぞれの画像の内容を賢明に表し、3番目の画像は不正確です。

学習率、運動量、バッチサイズなどの学習パラメータを最適化します。単語や画像表現のドロップアウトやウェイトディケイのような正則化パラメータ、文脈サイズ、加算的または乗法的バージョンの使用の有無、単語埋め込みのサイズ、およびマルチモーダル表現サイズ1のようなアーキテクチャパラメータを含む。最終パラメータは、要素の数であり、乗法モデル。これは、それが過パラメータ空間の半分にのみ関連するので、興味深い課題を追加する。合計11のハイパーパラメータが得られます。この数字は小さく見えますが、この問題は、その最適化を非常に困難にする多くの課題を提供します。例えば、一般性を失わないために、ハイパーパラメータのための広範なボックス制約を選択する。しかし、これはモデル空間の大部分を実行不可能にする。さらに、ハイパーパラメータのかなりの部分がカテゴリに分かれており、客観的な表面に重大な非定常性が導入されています。

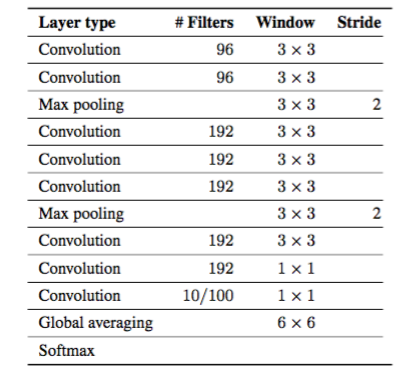
表3.我々の畳み込みニューラルネットワークアーキテクチャ。この選択は、最大限に一般的になるように選択されました。各畳み込み層の後にReLU非線形性が続く。

（クラスタの可用性によって決定される）300〜800回の実験を並行して実行して、我々は1週間未満で約2,500のCPU日に相当する2500回の実験を提案し、評価した。 BLEU-4メトリックを使用して、検証セット性能を最適化し、DNGOによって発見された最良LBLモデルは、LSTMリカレントニューラルネットワークを使用して最近提案されたモデルよりも優れています（Zaremba et al。、2015; Xu et al。、2015）。テストセット。
LBLは比較的単純なアプローチなので、これは注目に値する。この上位モデルを第2位および第3位の（LBLモデルの下で）LBLモデルでアンサンブルすると、LSTMベースのアプローチを大幅に上回るテストセットのBLEUスコア2が26.7になりました。我々は、ハイパーパラメータ空間に明確な複数の局所的な最適化が存在することに気付きました。これは少数のモデルの集合から劇的な改善を説明するかもしれません。我々は、図3のテスト画像上に生成されたキャプションの定性的な例を示している。ベイジアン最適化の反復の関数としてのBLEUスコアを示すさらなる図が補足説明書に記載されている。

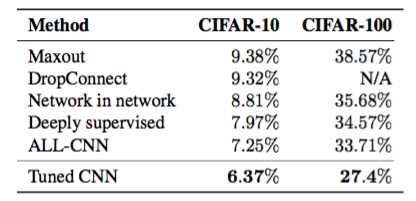
表4.畳み込みニューラルネットワークのさまざまなハイパーパラメータの関数として検証セット誤差を最適化するために我々のアルゴリズムを使用する。現在の最先端の結果と比較して、最適な超過パラメータ構成を備えたモデルの試験誤差を報告する。

4.3 畳み込みニューラルネットワーク

最後に、競争の激しいディープ学習ビジュアルオブジェクト認識ベンチマーク問題のペアに対してDNGOを使用します。 CIFAR-10およびCIFAR-100データセットで、深い畳み込みニューラルネットワークのハイパーパラメータを調整します。私たちのアプローチは、単一のジェネリックアーキテクチャを確立し、それを個別化されたハイパーパラメータチューニングを介してさまざまなタスクに特化させることです。そのため、両方のデータセットで、Springenbergらが提案した構成に基づいた同じ汎用アーキテクチャーを採用しました。 （2014年）、これは強い分類結果を達成することが示された。このアーキテクチャの詳細は表5を参照してください。

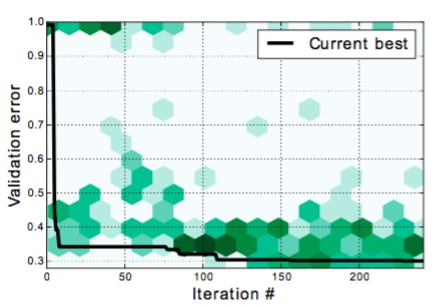
このアーキテクチャでは、運動量、学習速度、体重減衰係数、脱落率、ランダムi.i.dの標準偏差を調整しました。ガウシアン重み初期化、色相、彩度と値のグローバルな摂動、ランダムスケーリング、入力ピクセルのドロップアウト、ランダムな水平反射など、さまざまなデータ補強の破損範囲が含まれます。各ネットワークを200エポックで実行するトレーニングセットから引き出された10,000個の例の検証セットでこれらを最適化しました。ハイパーパラメータチューニング手順の視覚化については、図4を参照してください。
インテル®RECEIVE®Xeon PhiTMコプロセッサーの効率的な計算のために高度に最適化されたカーネル・ライブラリーを使用して、40個のジョブが並行して実行されているインテル®Xeon®Phi™コプロセッサーのクラスターで最適化を実行しました3。最適なハイパーパラメータ構成が見つかるように、トレーニングセット全体で350エポックの最終実験を行い、その結果を報告しました。

CIFAR-10とCIFAR-100の最適モデルはそれぞれ6.37％と27.4％のテスト誤差を達成しました。公表された最先端の結果（Goodfellow et al。、2013; Wan et al。、2013; Lin et al。、2013; Lee et al。、2014; Springenberg et al。、2014）表4に示されています。並列化された自動化されたハイパーパラメータ調整手順では、数段階の手順で最先端技術との競争力の高いモデルが得られます。
補足資料には、セットアップ、アーキテクチャ、チューニング、最適構成の包括的な概要が記載されています。

図4.時間の経過とともに評価された異なるハイパーパラメータ構成に対応するCIFAR-100での検証エラー。これらは平面ヒストグラムとして表され、各ビンの陰影はその中の総カウントを示す。発見された現在の最高の評価エラーは、黒でトレースされています。この投影法は、ベイジアン最適化の探索と搾取のパラダイムを示しています。このアルゴリズムでは、宇宙の未知の部分をトレードオフし、約束を示す部分に焦点を当てます。

5. 結論

本稿では、騒々しい高価なブラックボックス機能の効率的な最適化を可能にするグローバルオプティマイゼーションのためのディープネットワーク、すなわちDNGOを導入した。このモデルは、摂動性や不確実性の原則的な管理など、GPの望ましい特性を維持しますが、観察数の関数として、立方体から線形へのスケーラビリティを大幅に改善します。このモデルでは効率的な計算が可能ですが、ベイジアン最適化のための既存の最先端技術と競合しています。我々は、大規模パラレル最適化に特に適していることを実証している。
ニューラルネットワークを用いた適応基底回帰は、スケーラビリティの向上に対する1つのアプローチを提供しますが、他のモデルもまた有望です。 1つの有望な作業ライン、例えばNickson et al。 （Snelson＆Ghahramani、2005; Titsias、2009; Hensman et al。、2013）と同様の方法論を導入することである（2014）。

6. 謝辞

この研究は、米国エネルギー省DE-AC02-05CH11231の下にあるAdvanced Energy Computing Research、Director of Science、Director of Scienceのディレクターによって支援されました。この研究では、米国エネルギー省科学技術庁の契約番号DE-AC02-05CH11231の下でサポートされている国立エネルギー研究科学計算センターのリソースを使用しました。私たちは、BERBEE XEON PHIのテストベッドへの十分なアクセスを提供してくれたNERSCシステムのスタッフ、特にHelen HeとHarvey Wassermanに感謝したいと思います。
この論文の画像キャプション生成の計算は、ハーバード大学のFAS科学研究部コンピューティンググループによってサポートされているオデッセイクラスターで実行されました。私たちはFASRCのスタッフ、特にオデッセイへの寛大なアクセスを提供してくれたJames Cuffに感謝したいと思います。
Jasper Snoekは、ハーバード・コンピューティング・リサーチセンターの研究員です。 Kevin Swerskyは、オンタリオ大学院奨学金（OGS）の受領者です。この研究の一部は、NSF IIS-1421780、カナダの自然科学およびエンジニアリング研究評議会（NSERC）およびカナダ研究高等研究院（CIFAR）によって資金提供されました。

#補足資料

A. 畳み込みニューラルネットワーク実験仕様

このセクションでは、ネットワークアーキテクチャー、トレーニング、およびメタ最適化の詳細について説明します。以下のサブセクションでは、ハイパーパラメータ化スキームについて詳述する。 2つのデータセットのハイパーパラメータとその最適構成に関するプリオリは表6にあります。

A.1 アーキテクチャ

モデルのアーキテクチャは表5のとおりです。

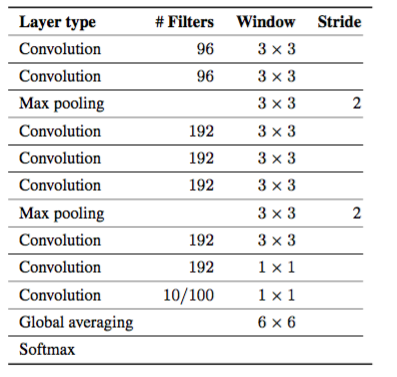
表5.畳み込みニューラルネットワークアーキテクチャこの選択は、最大限に一般的になるように選択されました。各畳み込み層の後にReLU非線形性が続く。

A.2 データ拡張

私たちは、さまざまな方法で各入力を壊しています。以下では、これらの腐敗のパラメータ化について説明します。

HSV

グローバル定数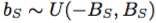、、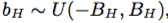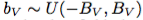によって、各入力の色相、彩度、および値フィールドをシフトします。同様に、我々は全体的に彩度を伸ばす
およびグローバル定数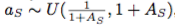、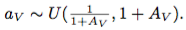による値フィールド。

スケーリング

各入力は、ある係数
によってスケーリングされる。

トランスレーション

我々は、各入力を27×27の大きさに切り抜く。ここでは、ウィンドウはランダムかつ一様に選択される。

水平反射

各入力は水平に反映され、確率は0.5です。

ピクセルドロップアウト

各入力要素は、ランダムに確率D0で独立して同一にドロップされます。

A.3 初期化とトレーニング手順

各畳み込み層mの重みを、標準偏差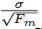
のi.i.dゼロ平均ガウス分布で初期化する。ここで、Fmは
Fmは、そのレイヤのフィルタあたりのパラメータの数です。我々はこれを選んだ
パラメータの次元をフィルタリングするために分散が不変なアクティベーションを生成します。私たちは入力以外のすべてのレイヤーに同じ標準偏差を使用します。これは、ネットワーク内のより深いレイヤーから独自のハイパーパラメータσIを使用します。

標準的な確率勾配降下および運動量最適化を使用してモデルを訓練する。我々は128のミニバッチサイズを使用し、運動量と学習率を調整します。これはそれぞれ1 - $0.1^M$と$0.1^L$としてパラメータ化されます。我々は、エポック130,190で学習率を0.1倍にアニールする。我々は200エポック後にトレーニングを終了する。

すべての層の重みを体重減衰係数Wで正規化する。最大プール層の出力にドロップアウトを適用し、これらのレートD1、D2を別々に調整します。

A.4 試験手順

学習したモデルの性能は、入力破損分布から抽出した100個の標本に対する対数確率予測を平均し、単位ドロップアウト分布からマスクを引き出して評価します。

B. 画像キャプションの生成に関する追加の数字

図5（a）および5（b）では、ベイジアン最適化ルーチンの動作を強調するセクション4.2からの画像キャプション生成実験の結果のいくつかの付加的な視覚化を提供する。両方の図は、最適化手順の反復で評価された異なるハイパーパラメータ構成に対応するMS COCOのBLEU-4スコアの検証を示しています。図5（a）において、これらは平面ヒストグラムとして表され、各ビンの陰影はその中の総数を示す。発見された現在の最高妥当性スコアは黒でトレースされています。図5（b）は、すべての実験の検証スコアの散布図を、終了した順に示しています。検証のスコア0は、制約違反に対応します。これらの図は、Bayesian Optimizationの探査と搾取のパラダイムを示しています。このパラダイムでは、アルゴリズムは空間の未踏の部分をトレードオフし、約束を示す部分に焦点を当てます。

C.マルチモーダル神経言語モデルのハイパーパラメータ

C.1 ハイパーパラメータの説明

我々は、ログ双線形モデル（LBL）の合計11のハイパーパラメータを最適化する。以下では、これらのハイパーパラメータが参照するものについて説明します。

モデル

LBLモデルには、画像特徴が加法的バイアス項を介して組み込まれる加法モデルと、モダリティ間の相互作用を制御するために因子分解された加重テンソルを使用する乗法という2つの変種がある。

コンテキストサイズ

LBLの目標は、一連の単語が与えられたときに次の単語を予測することです。コンテキストサイズは、このシーケンス内の単語の数を指定します。

学習率、運動量、バッチサイズ

これらは、LBLモデルパラメータの確率的勾配学習の際に使用される最適化パラメータです。学習率に対する最適化はログ空間で実行されるが、提案された学習率は訓練手順に渡される前に評価される。

非表示のレイヤーサイズ

これは、単語や画像のジョイント隠し表現のサイズを制御します。

埋め込みサイズ

単語は、ワンホットベクトルではなく、フィーチャー埋め込みによって表現されます。これは埋め込みの次元です。

Dropout

隠しレイヤーに追加するドロップアウトの量を決定する正規化パラメーター。

文脈崩壊、単語崩壊

入力重みと出力重みのL2正規化。学習率と同様に、これらはログの空間で最適化され、数桁の大きさで変化します。

Factors

体重テンソルの階数。乗法モデルにのみ関連します。

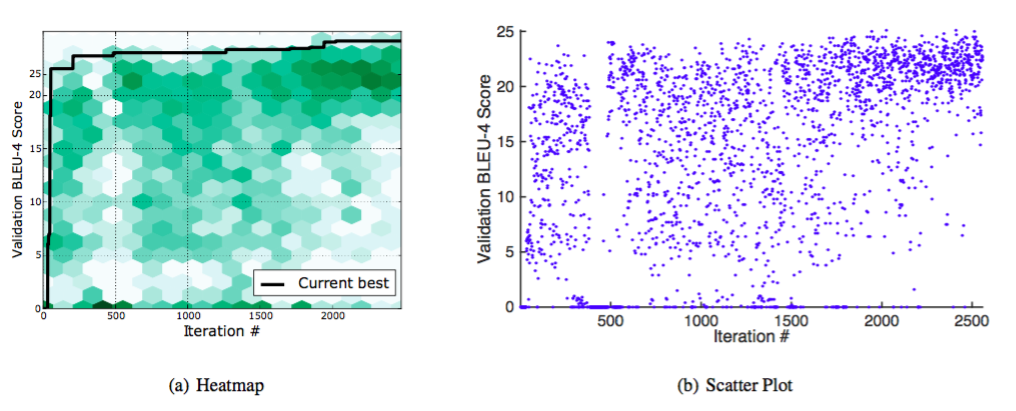
図5.時間の経過とともに評価された異なるハイパーパラメータ構成に対応するMS COCOのBLEU-4スコア。図5（a）において、これらは平面ヒストグラムとして表され、各ビンの陰影はその中の総カウントを示す。発見された現在の最高妥当性スコアは黒でトレースされています。図5（b）は、すべての実験の検証スコアの散布図を、終了した順に示しています。この投影法は、ベイジアン最適化の探査対搾取のパラダイムを示しています。このパラダイムでは、アルゴリズムは空間の未踏の部分をトレードオフし、約束を示す部分に焦点を当てます。

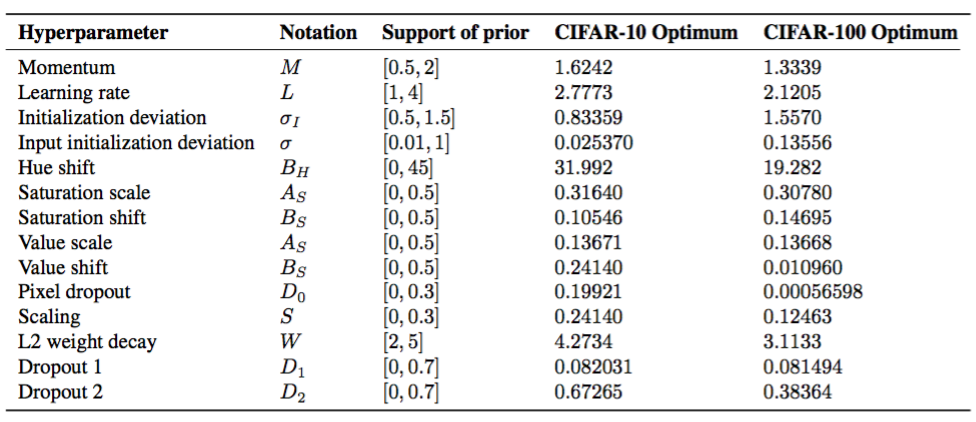
表6.ハイパーパラメータ化スキームの仕様、および最適なハイパーパラメータ構成が見つかりました。

#用語集
過程...過程とは元々時間tに関連した関数 f(t) に関して議論をするための言葉
確率過程...確率変数の集合 D={x,y} に関して議論するための手法群
ガウス分布...正規分布。山なりの分布
ガウスプロセス,ガウス過程...訓練データにガウス分布を与える

#GAでの最適化
ハイパーキューブベースのニューロエボリューショントポロジーの拡張（HyperNEAT）
http://qiita.com/miyamotok0105/items/7b7122908f154882c293