前回に引き続き,WaveNetの出力の確率分布を観察することで何か研究に活かせるようなアイデアが出るのでは、と思ったのでやってみた.
WaveNetから確率分布パラメータの獲得
この行で、WaveNetからのMoLの分布パラメータを出力している.この後のサンプリングで破壊的代入を行なっていたため,この行の出力もデータとして保存しておくことで確率分布のパラメータを獲得した.具体的には以下のようにした.
outputs = []
outputs_probability = []
try:
x = f.incremental_forward(x)
except AttributeError:
x = f(x)
#save output probability
outputs_probability += [x.data]
# T x B x C
outputs = torch.stack(outputs)
outputs_probability = torch.stack(outputs_probability)
# B x C x T
outputs = outputs.transpose(0, 1).transpose(1, 2).contiguous()
outputs_probability = outputs_probability.transpose(0,1).transpose(1,2).contiguous()
self.clear_buffer()
return (outputs, outputs_probability)
そして,synthesis.pyを以下のように修正して,獲得した.WaveNetから得た分布は,処理や可視化を簡単にするため、numpyに変換を行った.
with torch.no_grad():
y_hat, prob = model.incremental_forward(
initial_input, c=c, g=g, T=length, tqdm=tqdm, softmax=True, quantize=True,
log_scale_min=hparams.log_scale_min)
if is_mulaw_quantize(hparams.input_type):
y_hat = y_hat.max(1)[1].view(-1).long().cpu().data.numpy()
y_hat = P.inv_mulaw_quantize(y_hat, hparams.quantize_channels)
elif is_mulaw(hparams.input_type):
y_hat = P.inv_mulaw(y_hat.view(-1).cpu().data.numpy(), hparams.quantize_channels)
else:
y_hat = y_hat.view(-1).cpu().data.numpy()
return (y_hat, prob)
# DO generate
waveform, probability = wavegen(model, length, c=c, g=speaker_id, initial_value=initial_value, fast=True)
# save
librosa.output.write_wav(dst_wav_path, waveform, sr=hparams.sample_rate)
probability = probability.cpu().data.numpy()
dst_prob_path = join(dst_dir, '{}{}.npy'.format(checkpoint_name, file_name_suffix))
np.save(dst_prob_path, probability, allow_pickle=False)
分析内容
WaveNetの合成に時間がかかるため,LJ Speechの以下のセンテンスを読み上げたメルスペクトログラムを用いた合成音声のみで分析を試みた.
Printing, in the only sense with which we are at present concerned, differs from most if not from all the arts and crafts represented in the Exhibition
この音声波形と,各音素とロジスティック分布のパラメータ$s$との関係をヒートマップで可視化した.その後、ある音素の最大及び最小の$s$の時の近似分布をプロットする、ということを行った.
ヒートマップでの可視化
音素とパラメータ$s$の対応関係を可視化しようと考えた理由は,このパラメータがガウス分布での分散に相当するパラメータであることから,音素によってプロットされる確率の不確実さが分かるのではないかと考えた.例えば、濁点のようなノイジーな成分では分散を大きくすることで高周波の再現をする,と言った動的な予測をしているのではと考えた.
コード全体は以下のようになる.
import numpy as np
import pandas as pd
import librosa
import matplotlib.pyplot as plt
import os
import json
import seaborn as sns
# alignの獲得
json_open = open('./align_LJ/align.json', 'r')
json_load = json.load(json_open)
align = json_load['words']
# 16kHzで処理されているので,22.5kHzのサンプル長に修正する
# duration * 22050で長さの変換ができる
wav, fs = librosa.load('LJ001-0001.wav')
frame_align = np.array(['silence' for _ in range(len(wav))])
for word in align:
start = int(word['start'] * fs)
for phone in word['phones']:
duration = int(phone['duration'] * fs)
frame_align[start:start + duration] = phone['phone']
start += duration
# WaveNetの出力分布のパラメータを読み込み
prob = np.load('./20180510_mixture_lj_checkpoint_step000320000_ema.npy')
prob_cut = prob[0,0,:,:] #データが[1, 1, t, 30]となっているため
uni = np.random.uniform(1e-5, 1.0-1e-5, 10)
temp = prob_cut[:,:10] - np.log(-np.log(uni))
argmax = temp.argmax(axis=-1).astype(np.int)
u_arg, s_arg = argmax+10, argmax+20
u = np.array([prob_cut[i,arg] for i, arg in enumerate(u_arg)])
s = np.array([prob_cut[i,arg] for i, arg in enumerate(s_arg)])
e_s = np.exp(s)#WaveNetではパラメータsが対数をとって学習されているため,ここで変換
# それぞれの音素におけるパラメータsの値を獲得
phoneme_count = {}
for i in range(len(frame_align)):
if frame_align[i] not in phoneme_count:
phoneme_count[frame_align[i]] = []
phoneme_count[frame_align[i]].append(e_s[i])
else:
phoneme_count[frame_align[i]].append(e_s[i])
# ヒートマップの作製
phoneme_hist = []
phoneme_key = list(phoneme_count.keys())
phoneme_key = sorted(phoneme_key)
for phoneme in phoneme_key:
hist, bins = np.histogram(np.array(phoneme_count[phoneme]), bins=100, range=(e_s.min(),e_s.max()))
phoneme_hist.append(hist/hist.max())#normalization
phoneme_hist = np.array(phoneme_hist)
bins_str = ['{:.2e}'.format(bi) for bi in bins] #可視化のために,浮動小数点表示に変換
heatmap = pd.DataFrame(phoneme_hist, index=phoneme_key, columns=bins_str[:-1])
sns.heatmap(heatmap, robust=True, xticklabels=5, yticlabels=1)
処理の説明を以下で行う.
音素の獲得
音声−音素解析はgentleを用いて獲得した.しかし,gentleでは音声を16kHzに変換して処理を行っているため,LJSpeechのサンプリング周波数である22.5kHzに音声長を変換する必要がある.その処理を以下のコードで実行している.
# alignの獲得
json_open = open('./align_LJ/align.json', 'r')
json_load = json.load(json_open)
align = json_load['words']
# 16kHzで処理されているので,22.5kHzのサンプル長に修正する
# duration * 22050で長さの変換ができる
wav, fs = librosa.load('LJ001-0001.wav')
frame_align = np.array(['silence' for _ in range(len(wav))])
for word in align:
start = int(word['start'] * fs)
for phone in word['phones']:
duration = int(phone['duration'] * fs)
frame_align[start:start + duration] = phone['phone']
start += duration
分布パラメータの獲得
以下が実行コードである.
prob = np.load('./20180510_mixture_lj_checkpoint_step000320000_ema.npy') #WaveNetの出力分布のパラメータ
prob_cut = prob[0,0,:,:] #データが[1, 1, t, 30]となっているため
uni = np.random.uniform(1e-5, 1.0-1e-5, 10)
temp = prob_cut[:,:10] - np.log(-np.log(uni))
argmax = temp.argmax(axis=-1).astype(np.int)
u_arg, s_arg = argmax+10, argmax+20
u = np.array([prob_cut[i,arg] for i, arg in enumerate(u_arg)])
s = np.array([prob_cut[i,arg] for i, arg in enumerate(s_arg)])
e_s = np.exp(s)#WaveNetではパラメータsが対数をとって学習されているため,ここで変換
パラメータ$\mu,s$の選択は,元の実装と同様にlogit_probからサンプリングを行い値を獲得する.
音素と分布パラメータとの対応付け
最後に,音素と分布パラメータ$s$の対応付けを行い,それぞれの音素ごとにヒストグラムを作成して連結した.
# それぞれの音素におけるパラメータsの値を獲得
phoneme_count = {}
for i in range(len(frame_align)):
if frame_align[i] not in phoneme_count:
phoneme_count[frame_align[i]] = []
phoneme_count[frame_align[i]].append(e_s[i])
else:
phoneme_count[frame_align[i]].append(e_s[i])
# ヒートマップの作製
phoneme_hist = []
phoneme_key = list(phoneme_count.keys())
phoneme_key = sorted(phoneme_key)
for phoneme in phoneme_key:
hist, bins = np.histogram(np.array(phoneme_count[phoneme]), bins=100, range=(e_s.min(),e_s.max()))
phoneme_hist.append(hist/hist.max())#可視化のため正規化
phoneme_hist = np.array(phoneme_hist)
bins_str = ['{:.2e}'.format(bi) for bi in bins] #可視化のために,浮動小数点表示に変換
heatmap = pd.DataFrame(phoneme_hist, index=phoneme_key, columns=bins_str[:-1])
sns.heatmap(heatmap, robust=True, xticklabels=5, yticlabels=1)
分析結果
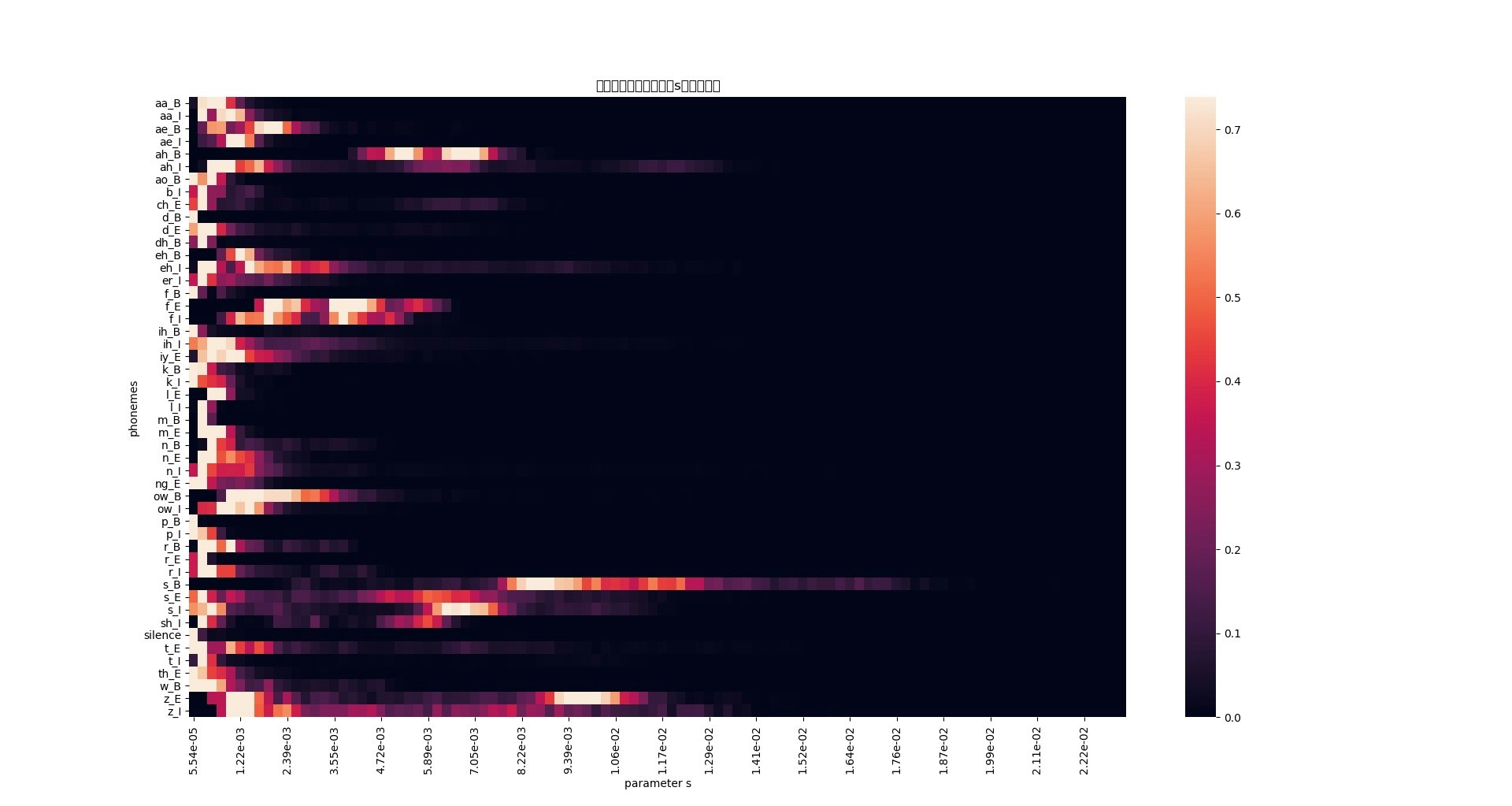
結果は以下のようになった.
横軸はパラメータ$s$で,右にいくほど分散が大きくなる.縦軸は音素で,○_Bは単語の最初にくる音素,○_Eは単語の終わりに読まれる音素,○ _Iは単語の中間に出現する音素である.
データをパッとみた感想
「s_B」(スー、と言った空気の漏れるような発音)や、「z_E」(ズッ、と言いた濁音)等、比較的ノイジーな音素で分散が大きく、また取りうる値の幅も広いことがわかる。しかし、分散が大きい音素の中には「ah_B」(単語「are」の最初の発音)のような一見ノイジーではない音素もある。
一方、「silence」(無音区間)では分散が常に小さく、ほとんど決定的な値を取っていることもわかる。
音素「s_B」の分析
こと音素「s_B」は取りうるパラメータの幅が広いため、この音素の$s$が最大と最小の時の確率分布をプロットして、データの可視化を行なってみた。
分布の可視化
分布の可視化は,以下のコードで行う.
mean_uni = np.random.uniform(1e-5, 1.0-1e-5, (len(u), 500))
px = u[:,np.newaxis] + np.exp(s[:,np.newaxis]) * (np.log(mean_uni) - np.log(1.0 - mean_uni)) #近似分布の獲得
sns.distplot(px[i]) #任意の時刻の分布を可視化
こちらも元の実装と同様に一様分布からのサンプリングで値を獲得する.違いとして,同じ分布パラメータで複数回のサンプリングを行い,ヒストグラムを用いて近似分布として可視化する.
確率密度関数をプロットしない理由
ロジスティックス分布の確率密度関数は以下の式である.
p(x;\mu,s) = \frac{\exp(-\frac{x-\mu}{s})}{s(1+\exp(-\frac{x-\mu}{s}))^2}
今回用いるパラメータ$s$は,およそ$10^{-6}\leq s \leq 10^{-2}$の値を取る.$x = \mu$の時に,確率密度が最小,最大で1000倍近い差が生じてしまい,可読性に欠けるため,サンプリングによる近似分布で比較を行う.
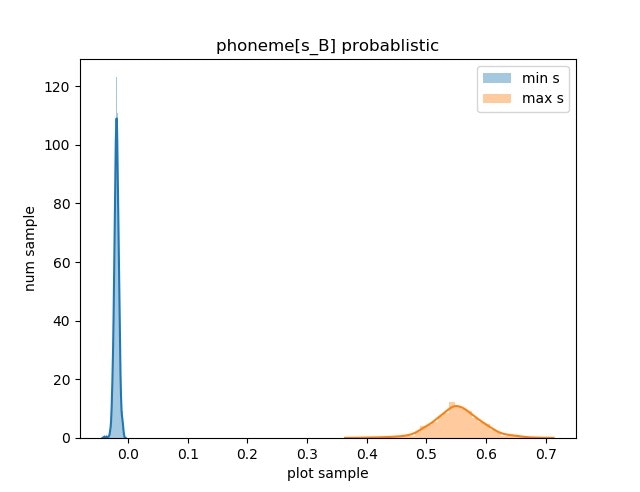
可視化結果
横軸はサンプリングによって得た値で、音声波形の振幅に相当する。WaveNetの出力は-1~1の範囲で出力される。縦軸はサンプリングによって出力された値の頻度である。
可視化した感想
もっと分散が大きく,一様分布のようなランダム性の高い分布になると考えていた.しかし,結果的にはロジスティックス分布の形状を維持していて予測が外れてしまった.
考察
ヒートマップ,及び音素「s_B」の分布の可視化を行った.音素「s_B」の場合,振幅の大きい,つまり平均$\mu$が大きいときに分散が最も大きく,$\mu$の値が小さいときに分散も小さかった.このことから,平均$\mu$の大きさと$s$の値に相関があり,振幅が大きな場合に不確実さをより大きくすることで「スー」っといったノイジーな音声を表現しているのでは,と考えた.この点においてはまだ分析をしていないので今後データの観察を行いたい.
まとめ
音素とWaveNetの出力分布のパラメータとの関係の可視化を行い,分析してみた.まだまだ分析し足りない要素があると感じたことと,音素と音声波形に関する先行研究や知見の調査が不足しているなと感じたため,今後はそちら側の情報も収集しようと考えている.データ分析は難しいが,データをあれこれ操作しているのは楽しいので定期的に行っていきたい.