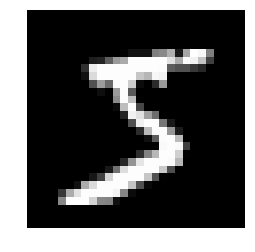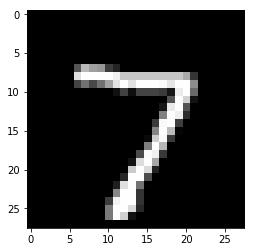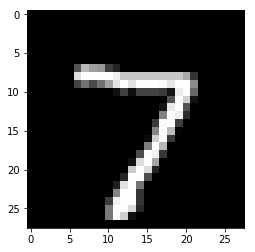Update (2018/04/20): Chainer v4に合わせ内容を更新しました。
注意:
- 今回はニューラルネットワーク自体が何なのかといった説明は省きます。
- この記事はJupyter notebookを使って書かれていますので、コードは上から順番に実行できるようにチェックされています。元のJupyter notebookファイルはGoogle Colabを使ってブラウザから実行することができます。Google Colab上ではGPUを使った学習を実際に実行することができますので、「ドライブにコピー」ボタンをクリックしてご自分のドライブにコピーしてから、ぜひ実行してみてください。:Chainer Beginner's Hands-on.ipynb
Qiitaだとページ内リンクつきの目次が勝手に作成されるので、全体概要はそちらを眺めて把握してください。
インストール
Chainerのインストールはとても簡単です。Chainer本体はすべてPythonコードのみからなるので、インストールも
%%bash
pip install chainer
で完了です。ただ、これだけではGPUは使えません。GPUを使うためには、**別途CuPyをインストールする必要があります。**ただCuPyのインストールもとても簡単です。
%%bash
pip install cupy-cuda90
以上です。筆者の環境がCUDA9.0の環境であったためcupy-cuda90をインストールしていますが、この末尾の2つの数字はCUDAのバージョンを表しています。お使いの環境のCUDAバージョンに合わせて、
-
cupy-cuda80(CUDA 8.0用) -
cupy-cuda90(CUDA9.0用) -
cupy-cuda91(CUDA9.1用)
の3つから適切なものを選択してpip installしてください。CuPy v4.0.0からwheelでのインストールが可能となりましたので、これにより自動的にcuDNNやNCCL2といったライブラリもインストールされ、CuPyから使用可能になります。(cuDNNを独立に取ってくる方法を注に書いておきます1)
また、Chainer v4.0.0からchainer.print_runtime_info()という便利なメソッドが追加されました。以下のコマンドをターミナルで実行し、ChainerやCuPyが正しくインストールされたかを確認してみましょう。
%%bash
python -c 'import chainer; chainer.print_runtime_info()'
Chainer: 4.0.0
NumPy: 1.14.0
CuPy:
CuPy Version : 4.0.0
CUDA Root : /usr/local/cuda
CUDA Build Version : 9000
CUDA Driver Version : 9000
CUDA Runtime Version : 9000
cuDNN Build Version : 7102
cuDNN Version : 7005
NCCL Build Version : 2104
うまくできていますね。以下のチュートリアルでは、matplotlibを可視化に使いますので、これも同時にインストールしておきましょう。
%%bash
pip install matplotlib
また、計算グラフの可視化にGraphvizを使いますので、こちらもインストールしておいてください。
学習ループを書いてみよう
ここでは、有名な手書き数字のデータセットMNISTを使って、画像を10クラスに分類するネットワークを書いて訓練してみます。
1. データセットの準備
教師あり学習の場合、データセットは「入力データ」と「それと対になるラベルデータ」を返すオブジェクトである必要があります。
ChainerにはMNISTやCIFAR10/100のようなよく用いられるデータセットに対して、データをダウンロードしてくるところからそのような機能をもったオブジェクトを作るところまで自動的にやってくれる便利なメソッドがあるので、ここではひとまずこれを用いましょう。
from chainer.datasets import mnist
# データセットがダウンロード済みでなければ、ダウンロードも行う
train_val, test = mnist.get_mnist(withlabel=True, ndim=1)
データセットオブジェクト自体は準備ができました。これは、例えば train_val[i] などとするとi番目の (data, label) というタプルを返すリスト と同様のものになっています(実際ただのPythonリストもChainerのデータセットオブジェクトとして使えます)。では0番目のデータとラベルを取り出して、表示してみましょう。
# matplotlibを使ったグラフ描画結果がnotebook内に表示されるようにします。
%matplotlib inline
import matplotlib.pyplot as plt
# データの例示
x, t = train_val[0] # 0番目の (data, label) を取り出す
plt.imshow(x.reshape(28, 28), cmap='gray')
plt.axis('off')
plt.show()
print('label:', t)
label: 5
1.1 Validation用データセットを作る
次に、上で作成したtrain_valデータセットを、Training用のデータセットとValidation用のデータセットに分割しましょう。これもChainerの便利な関数を使えば簡単にできます。元々60000個のデータが入っているtrainデータセット50000個のデータをTraining用に、残りの10000個をValidation用にしてみます。
from chainer.datasets import split_dataset_random
train, valid = split_dataset_random(train_val, 50000, seed=0)
これだけで元々のtrain_valを、ランダムに選んだ50000個のtrainデータセットとvalidデータセットに分けることができました。何度も実行する際に異なる分け方になってしまわないよう、第3引数のseedを設定しておくことをオススメします。それでは、それぞれのデータセットの中に入っているデータの数を確認してみましょう。
print('Training dataset size:', len(train))
print('Validation dataset size:', len(valid))
Training dataset size: 50000
Validation dataset size: 10000
2. Iteratorの作成
データセットの準備は完了しましたが、このままネットワークの学習に使うのは少し面倒です。なぜなら、ネットワークのパラメータ最適化手法として広く用いられているStochastic Gradient Descent (SGD)という手法では、一般的にいくつかのデータを束ねたミニバッチと呼ばれる単位でネットワークにデータを渡し、それに対する予測を作って、ラベルと比較するということを行います。そのため、バッチサイズ分だけデータとラベルを束ねる作業が必要です。
そこで、データセットから決まった数のデータとラベルを取得し、それらを束ねてミニバッチを作ってくれる機能を持ったIteratorを使いましょう。Iteratorは、先程作ったデータセットオブジェクトを渡して初期化してやったあとは、next()メソッドで新しいミニバッチを返してくれます。内部ではデータセットを何周なめたか(epoch)などの情報がどうように記録されているおり、学習ループを書いていく際に便利です。
データセットオブジェクトからイテレータを作るには、以下のようにします。
from chainer import iterators
batchsize = 128
train_iter = iterators.SerialIterator(train, batchsize)
valid_iter = iterators.SerialIterator(
valid, batchsize, repeat=False, shuffle=False)
test_iter = iterators.SerialIterator(
test, batchsize, repeat=False, shuffle=False)
ここでは、学習に用いるデータセット用のイテレータ(train_iter)と、検証用のデータセット用のイテレータ(valid_iter)、および学習したネットワークの評価に用いるテストデータセット用のイテレータ(test_iter)の計3つを作成しています。ここで、batchsize = 128としているので、作成した3つのIteratorは、例えばtrain_iter.next()などとすると128枚の数字画像データを一括りにして返してくれます。
NOTE: SerialIteratorについて
Chainerがいくつか用意しているIteratorの一種であるSerialIteratorは、データセットの中のデータを順番に取り出してくる最もシンプルなIteratorです。コンストラクタの引数にデータセットオブジェクトと、バッチサイズを取ります。このとき、渡したデータセットオブジェクトから、何周も何周もデータを繰り返し読み出す必要がある場合はrepeat引数をTrueとし、1周が終わったらそれ以上データを取り出したくない場合はこれをFalseとします。これは、主にvalidation用のデータセットに対して使うフラグです。デフォルトでは、Trueになっています。また、shuffle引数にTrueを渡すと、データセットから取り出されてくるデータの順番をエポックごとにランダムに変更します。SerialIteratorの他にも、マルチプロセスで高速にデータを処理できるようにしたMultiprocessIteratorやMultithreadIteratorなど、複数のIteratorが用意されています。詳しくは以下を見てください。
3. ネットワークの定義
では、学習させるネットワークを定義してみましょう。今回は、全結合層のみからなる多層パーセプトロンを作ってみます。中間層のユニット数は適当に100とし、今回は10クラス分類をしたいので、出力ユニット数は10とします。今回用いるMNISTデータセットは0〜9までの数字のいずれかを意味する10種のラベルを持つためです。では、ネットワークを定義するために必要なLink, Function, そしてChainについて、簡単にここで説明を行います。
LinkとFunction
Chainerでは、ニューラルネットワークの各層を、LinkとFunctionに区別します。
Linkは、パラメータを持つ関数です。Functionは、パラメータを持たない関数です。
これらを組み合わせてネットワークを記述します。パラメータを持つ層は、chainer.linksモジュール以下にたくさん用意されています。パラメータを持たない層は、chainer.functionsモジュール以下にたくさん用意されています。これらに簡単にアクセスするために、
import chainer.links as L
import chainer.functions as F
と別名を与えて、L.Convolution2D(...)やF.relu(...)のように用いる慣習がありますが、特にこれが決まった書き方というわけではありません。
Chain
Chainは、パラメータを持つ層(Link)をまとめておくためのクラスです。パラメータを持つということは、基本的にネットワークの学習の際にそれらを更新していく必要があるということです(更新されないパラメータを持たせることもできます)。Chainerでは、モデルのパラメータの更新は、Optimizerという機能が担います。その際、更新すべき全てのパラメータを簡単に発見できるように、Chainで一箇所にまとめておきます。そうすると、Chain.params()メソッドを使って更新されるパラメータ一覧が簡単に取得できます。
Chainを継承してネットワークを定義しよう
Chainerでは、ネットワークはChainクラスを継承したクラスとして定義されることが一般的です。その場合、そのクラスのコンストラクタで、self.init_scope()で作られるwithコンテキストを作り、その中でネットワークに登場するLinkをプロパティとして登録しておきます。こうすると、自動的にOptimizerが最適化対象のパラメータを持つ層だな、と捉えてくれます。
もう一つ、一般的なのは、ネットワークの前進計算(データを渡して、出力を返す)を、__call__メソッドに書いておくという方法です。こうすると、ネットワーククラスをinstantiateして作ったオブジェクトを、関数のようにして使うことができます(例:output = net(data))。
GPUで実行するには
Chainクラスはto_gpuメソッドを持ち、この引数にGPU IDを指定すると、指定したGPU IDのメモリ上にネットワークの全パラメータを転送します。こうしておくと、前進計算も学習の際のパラメータ更新なども全部GPU上で行われるようになります。GPU IDとして-1を使うと、すなわちこれはCPUを意味します。
同じ結果を保証したい
ネットワークを書き始める前に、まずは乱数シードを固定して、本記事とほぼ同様の結果が再現できるようにしておきましょう。(cuDNNが有効になっている環境下でより厳密に計算結果の再現性を保証したい場合は、chainer.config.cudnn_deterministicというConfiguringオプションについて知る必要があります。こちらのドキュメントを参照してください:chainer.config.cudnn_deterministic。
import random
import numpy
import chainer
def reset_seed(seed=0):
random.seed(seed)
numpy.random.seed(seed)
if chainer.cuda.available:
chainer.cuda.cupy.random.seed(seed)
reset_seed(0)
ネットワークを表すコード
いよいよネットワークを書いてみます!
import chainer
import chainer.links as L
import chainer.functions as F
class MLP(chainer.Chain):
def __init__(self, n_mid_units=100, n_out=10):
super(MLP, self).__init__()
# パラメータを持つ層の登録
with self.init_scope():
self.l1 = L.Linear(None, n_mid_units)
self.l2 = L.Linear(n_mid_units, n_mid_units)
self.l3 = L.Linear(n_mid_units, n_out)
def __call__(self, x):
# データを受け取った際のforward計算を書く
h1 = F.relu(self.l1(x))
h2 = F.relu(self.l2(h1))
return self.l3(h2)
gpu_id = 0 # CPUを用いる場合は、この値を-1にしてください
net = MLP()
if gpu_id >= 0:
net.to_gpu(gpu_id)
できました!疑問点はありませんか?ちなみに、Chainerにはたくさんの学習可能なレイヤやパラメータを持たないレイヤが用意されています。ぜひ一度以下の一覧のページを見てみましょう。
Link一覧には、ニューラルネットワークによく用いられる全結合層や畳み込み層、LSTMなどや、ReLUなどの活性化関数などなどだけでなく、有名なネットワーク全体もLinkとして載っています。ResNetや、VGGなどです。また、Function一覧には、画像の大きさをresizeしたり、サイン・コサインのような関数を始め、いろいろなネットワークの要素として使える関数が載っています。
NOTE
上のネットワーク定義で、L.Linearは全結合層を意味しますが、最初のLinear層は第一引数にNoneが渡されています。これは、実行時に、つまりデータがその層に入力された瞬間、必要な数の入力側ユニット数を自動的に計算するということを意味します。ネットワークが最初に計算を行う際に、初めて (n_input) $\times$ n_mid_units の大きさの行列を作成し、それを学習対象とするパラメータとして保持します。これは後々、畳み込み層を全結合層の前に配置する際などに便利な機能です。
様々なLinkは、それぞれ学習対象となるパラメータを保持しています。それらの値は、NumPyの配列として簡単に取り出して見ることができます。例えば、上のモデルMLPはl1という名前の全結合層が登録されています。この全結合層は重み行列Wとバイアスbという2つのパラメータを持ちます。これらには外から以下のようにしてアクセスすることができます:
print('1つ目の全結合層のバイアスパラメータの形は、', net.l1.b.shape)
print('初期化直後のその値は、', net.l1.b.array)
1つ目の全結合層のバイアスパラメータの形は、 (100,)
初期化直後のその値は、 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0.]
しかしここで、net.l1.W.arrayの中身を同様に表示してみようとすると、Noneが返されます。
print(net.l1.W.array)
None
なぜでしょうか?我々はl1をネットワークに登録するときに、L.Linearの第一引数にNoneを渡しましたね。そして、まだネットワークに一度もデータを入力していません。そのため、**まだ重み行列Wは作成されていません。**そのため、まだnet.l1.Wは具体的な配列を保持していないのです。
4. 最適化手法の選択
では、上で定義したネットワークをMNISTデータセットを使って訓練してみましょう。学習時に用いる最適化の手法としてはいろいろな種類のものが提案されていますが、Chainerは多くの手法を同一のインターフェースで利用できるよう、Optimizerという機能でそれらを提供しています。chainer.optimizersモジュール以下に色々なものを見つけることができます。一覧はこちらにあります:
ここでは最もシンプルな勾配降下法の手法であるoptimizers.SGDを用います。Optimizerのオブジェクトには、setupメソッドを使ってモデル(Chainオブジェクト)を渡します。こうすることでOptimizerに、何を最適化すればいいか把握させることができます。
他にもいろいろな最適化手法が手軽に試せるので、色々と試してみて結果の変化を見てみてください。例えば、下のchainer.optimizers.SGDのうちSGDの部分をMomentumSGD, RMSprop, Adamなどに変えるだけで、最適化手法の違いがどのような学習曲線(ロスカーブ)の違いを生むかなどを簡単に調べることができます。
from chainer import optimizers
optimizer = optimizers.SGD(lr=0.01).setup(net)
NOTE
今回はSGDのコンストラクタのlrという引数に $0.01$ を与えました。この値は学習率として知られ、モデルをうまく訓練して良いパフォーマンスを発揮させるために調整する必要がある重要なハイパーパラメータとして知られています。
5. 学習する
いよいよ学習をスタートします!今回は分類問題なので、softmax_cross_entropyというロス関数を使って最小化すべきロスの値を計算します。
まず、ネットワークにデータを渡して、出てきた出力と、入力データに対応する正解ラベルを、Functionの一種でありスカラ値を返すロス関数に渡し、ロス(最小化したい値)の計算を行います。ロスは、chainer.Variableのオブジェクトになっています。そして、このVariableは、**今まで自分にどんな計算が施されたかを辿れるようになっています。**この仕組みが、Define-by-Run [Tokui 2015]とよばれる発明の中心的な役割を果たしています。
ここでは誤差逆伝播法自体の説明は割愛しますが、計算したロスに対する勾配をネットワークに逆向きに流していく処理は、Chainerではネットワークが吐き出したVariableが持つbackward()メソッドを呼ぶだけでできます。これを呼ぶと、前述のようにこれまでの計算過程を逆向きに遡って誤差逆伝播用の計算グラフを構築し、途中のパラメータの勾配を連鎖率を使って計算してくれます。(詳しくは筆者が日本ソフトウェア科学会で行ったチュートリアルの資料をご覧ください。)
こうして計算された各パラメータに対する勾配を使って、先程Optimizerを作成する際に指定したアルゴリズムを使ってネットワークパラメータの更新(=学習)が行われるわけです。
まとめると、今回1回の更新処理の中で行うのは、以下の4項目です。
- ネットワークにデータを渡して出力
yを得る - 出力
yと正解ラベルtを使って、最小化すべきロスの値をsoftmax_cross_entropy関数で計算する -
softmax_cross_entropy関数の出力(Variable)のbackward()メソッドを呼んで、ネットワークの全てのパラメータの勾配を誤差逆伝播法で計算する - Optimizerの
updateメソッドを呼び、3.で計算した勾配を使って全パラメータを更新する
パラメータの更新は、何度も何度も繰り返し行います。一度の更新に用いられるデータは、ネットワークに入力されたバッチサイズ分だけ束ねられたデータのみです。そのため、データセット全体のデータを使うために、次のミニバッチを入力して再度更新、その次のミニバッチを使ってまた更新、ということを繰り返すわけです。そのため、この過程を学習ループと呼んでいます。
NOTE: ロス関数
ちなみに、ロス関数は、例えば分類問題ではなく簡単な回帰問題を解きたいような場合、F.softmax_cross_entropyの代わりにF.mean_squared_errorなどを用いることもできます。他にも、いろいろな問題設定に対応するために様々なロス関数がChainerには用意されています。こちらからその一覧を見ることができます:
学習ループのコード
import numpy as np
from chainer.dataset import concat_examples
from chainer.cuda import to_cpu
max_epoch = 10
while train_iter.epoch < max_epoch:
# ---------- 学習の1イテレーション ----------
train_batch = train_iter.next()
x, t = concat_examples(train_batch, gpu_id)
# 予測値の計算
y = net(x)
# ロスの計算
loss = F.softmax_cross_entropy(y, t)
# 勾配の計算
net.cleargrads()
loss.backward()
# パラメータの更新
optimizer.update()
# --------------- ここまで ----------------
# 1エポック終了ごとにValidationデータに対する予測精度を測って、
# モデルの汎化性能が向上していることをチェックしよう
if train_iter.is_new_epoch: # 1 epochが終わったら
# ロスの表示
print('epoch:{:02d} train_loss:{:.04f} '.format(
train_iter.epoch, float(to_cpu(loss.data))), end='')
valid_losses = []
valid_accuracies = []
while True:
valid_batch = valid_iter.next()
x_valid, t_valid = concat_examples(valid_batch, gpu_id)
# Validationデータをforward
with chainer.using_config('train', False), \
chainer.using_config('enable_backprop', False):
y_valid = net(x_valid)
# ロスを計算
loss_valid = F.softmax_cross_entropy(y_valid, t_valid)
valid_losses.append(to_cpu(loss_valid.array))
# 精度を計算
accuracy = F.accuracy(y_valid, t_valid)
accuracy.to_cpu()
valid_accuracies.append(accuracy.array)
if valid_iter.is_new_epoch:
valid_iter.reset()
break
print('val_loss:{:.04f} val_accuracy:{:.04f}'.format(
np.mean(valid_losses), np.mean(valid_accuracies)))
# テストデータでの評価
test_accuracies = []
while True:
test_batch = test_iter.next()
x_test, t_test = concat_examples(test_batch, gpu_id)
# テストデータをforward
with chainer.using_config('train', False), \
chainer.using_config('enable_backprop', False):
y_test = net(x_test)
# 精度を計算
accuracy = F.accuracy(y_test, t_test)
accuracy.to_cpu()
test_accuracies.append(accuracy.array)
if test_iter.is_new_epoch:
test_iter.reset()
break
print('test_accuracy:{:.04f}'.format(np.mean(test_accuracies)))
epoch:01 train_loss:0.9393 val_loss:0.9708 val_accuracy:0.8019
epoch:02 train_loss:0.6163 val_loss:0.5335 val_accuracy:0.8650
epoch:03 train_loss:0.4596 val_loss:0.4236 val_accuracy:0.8835
epoch:04 train_loss:0.5109 val_loss:0.3750 val_accuracy:0.8931
epoch:05 train_loss:0.3167 val_loss:0.3449 val_accuracy:0.9017
epoch:06 train_loss:0.4418 val_loss:0.3263 val_accuracy:0.9074
epoch:07 train_loss:0.2389 val_loss:0.3103 val_accuracy:0.9122
epoch:08 train_loss:0.4076 val_loss:0.2977 val_accuracy:0.9149
epoch:09 train_loss:0.3687 val_loss:0.2930 val_accuracy:0.9151
epoch:10 train_loss:0.3271 val_loss:0.2800 val_accuracy:0.9190
test_accuracy:0.9375
val_accuracyに着目してみると、最終的におおよそ92%程度の精度で手書きの数字が分類できるようになりました。学習終了後に、ループの中でValidationデータセットを使ってモデルの汎化性能をおおまかにチェックしているのと同様にして、**テスト用のデータセットを用いて学習が終了したネットワークの評価を行っています。**テストデータでの評価結果は、およそ93.75%の正解率となりました。
5.1 ValidationやTestを行う際の注意点
ここで、ValidationにせよTestにせよ、「評価」を行う際には注意すべき点があります。学習は行わない、評価のためだけのデータをネットワークに渡して出力を計算している部分(例えば、y_test = net(x_test))では、それらの行を2つのコンテキストでくくっています。
chainer.using_config('train', False)
まず、今回は学習時と推論時で動作が異なる関数は含まれていないため、実際の効力は持ちませんが、Validationやテストのために推論を行うときはchainer.config.train = Falseとします。以下のように、chainer.using_config('train', False)をwith構文と共に使えば、その中ではchainer.config.train = Falseとなります。
with chainer.using_config('train', False):
--- 何か推論処理 ---
これは、以下のようにするのと同じことです。
chainer.config.train = False
--- 何か推論処理 ---
ただし、Pythonのコンテキストを利用しない場合は、一度このようにどこかで書くと、それ以降この設定はグローバルにずっと有効になることに注意してください。(推論したあと再び学習を行うという場合は、再度chainer.config.train = Trueなどのようにすることが必要になります。chainer.config以下の規定の値に何かを代入することはグローバルに作用しますので、次に説明するenable_backpropについても同様です。)
chainer.using_config('enable_backprop', False)
次に、今回は評価に用いる出力の計算後にロス関数の各パラメータについての勾配は必要ないので、内部に計算グラフを保持しておく必要もないため、chainer.using_config('enable_backprop', False)として無駄な計算グラフの構築を行わないようにし、メモリ消費量を節約しています。
NOTE: ChainerのConfig
Chainerにはこの他にも、いくつかのグローバルなConfigがプリセットとして用意されています。また、chainer.config以下にユーザが自由な設定値を置くこともできます。詳しくはこちらを一読してください:Configuring Chainer
6. 学習済みモデルを保存する
学習が終わったら、その結果を保存します。Chainerには、2種類のフォーマットで学習済みネットワークをシリアライズする機能が用意されています。一つはHDF5形式で、もう一つはNumPyのNPZ形式でネットワークを保存するものです。今回は、追加ライブラリのインストールが必要なHDF5ではなく、NumPy標準機能で提供されているシリアライズ機能(numpy.savez())を利用したNPZ形式でのモデルの保存を行います。
from chainer import serializers
serializers.save_npz('my_mnist.model', net)
# ちゃんと保存されていることを確認
%ls -la my_mnist.model
-rw-rw-r-- 1 shunta shunta 333944 Apr 22 00:52 my_mnist.model
7. 保存したモデルを読み込んで推論する
学習したネットワークを、それを使って数字の分類がしたい誰かに渡して、使ってもらうにはどうしたら良いでしょうか。もっともシンプルな方法は、ネットワークの定義がかかれたPythonファイルと、今しがた保存したNPZファイルを渡して、以下のように使うことです。以下のコードの前に、渡したネットワーク定義のファイルからネットワークのクラス(ここではMLP)が読み込まれていることを前提とします。
# まず同じネットワークのオブジェクトを作る
infer_net = MLP()
# そのオブジェクトに保存済みパラメータをロードする
serializers.load_npz('my_mnist.model', infer_net)
以上で準備が整いました。それでは、試しにテストデータの中から一つ目の画像を取ってきて、それに対する分類を行ってみましょう。
gpu_id = 0 # CPUで計算をしたい場合は、-1を指定してください
if gpu_id >= 0:
infer_net.to_gpu(gpu_id)
# 1つ目のテストデータを取り出します
x, t = test[0] # tは使わない
# どんな画像か表示してみます
plt.imshow(x.reshape(28, 28), cmap='gray')
plt.show()
# ミニバッチの形にする(複数の画像をまとめて推論に使いたい場合は、サイズnのミニバッチにしてまとめればよい)
print('元の形:', x.shape, end=' -> ')
x = x[None, ...]
print('ミニバッチの形にしたあと:', x.shape)
# ネットワークと同じデバイス上にデータを送る
x = infer_net.xp.asarray(x)
# モデルのforward関数に渡す
with chainer.using_config('train', False), chainer.using_config('enable_backprop', False):
y = infer_net(x)
# Variable形式で出てくるので中身を取り出す
y = y.array
# 結果をCPUに送る
y = to_cpu(y)
# 予測確率の最大値のインデックスを見る
pred_label = y.argmax(axis=1)
print('ネットワークの予測:', pred_label[0])
元の形: (784,) -> ミニバッチの形にしたあと: (1, 784)
ネットワークの予測: 7
ネットワークの予測は7でした。画像を見る限り、当たっていそうですね!
Trainerを使ってみよう
Chainerは、これまで書いてきたような学習ループを隠蔽するTrainerという機能を提供しています。これを使うと、学習ループを陽に書く必要がなくなり、またいろいろな便利なExtentionを使うことで、学習過程でのロスカーブの可視化や、ログの保存などが楽になります。
1. データセット・Iterator・ネットワークの準備
これらはループを自分で書く場合と同じなので、まとめてしまいます。
reset_seed(0)
train_val, test = mnist.get_mnist()
train, valid = split_dataset_random(train_val, 50000, seed=0)
batchsize = 128
train_iter = iterators.SerialIterator(train, batchsize)
valid_iter = iterators.SerialIterator(valid, batchsize, False, False)
test_iter = iterators.SerialIterator(test, batchsize, False, False)
gpu_id = 0 # CPUを用いたい場合は、-1を指定してください
net = MLP()
if gpu_id >= 0:
net.to_gpu(gpu_id)
2. Updaterの準備
ここからが学習ループを自分で書く場合と異なる部分です。ループを自分で書く場合には、データセットからバッチサイズ分のデータをとってきてミニバッチに束ねて、それをネットワークに入力して予測を作り、それを正解と比較し、ロスを計算してバックワード(誤差逆伝播)をして、Optimizerによってパラメータを更新する、というところまでを、以下のように書いていました。
# ---------- 学習の1イテレーション ----------
train_batch = train_iter.next()
x, t = concat_examples(train_batch, gpu_id)
# 予測値の計算
y = net(x)
# ロスの計算
loss = F.softmax_cross_entropy(y, t)
# 勾配の計算
net.cleargrads()
loss.backward()
# パラメータの更新
optimizer.update()
これらの処理を、まるっとUpdaterはまとめてくれます。これを行うために、UpdaterにはIteratorとOptimizerを渡してやります。 Iteratorはデータセットオブジェクトを持っていて、そこからミニバッチを作り、Optimizerは最適化対象のネットワークを持っていて、それを使って前進計算とロスの計算・パラメータのアップデートをすることができます。そのため、この2つを渡しておけば、上記の処理をUpdater内で全部行ってもらえるというわけです。では、Updaterオブジェクトを作成してみましょう。
from chainer import training
gpu_id = 0 # CPUを使いたい場合は-1を指定してください
# ネットワークをClassifierで包んで、ロスの計算などをモデルに含める
net = L.Classifier(net)
# 最適化手法の選択
optimizer = optimizers.SGD(lr=0.01).setup(net)
# UpdaterにIteratorとOptimizerを渡す
updater = training.StandardUpdater(train_iter, optimizer, device=gpu_id)
NOTE
ここでは、ネットワークをL.Classifierで包んでいます。L.Classifierは一種のChainになっていて、渡されたネットワーク自体をpredictorというattributeに持ち、**ロス計算を行う機能を追加してくれます。こうすると、net()はデータxだけでなくラベルtも取るようになり、まず渡されたデータをpredictorに通して予測を作り、それをtと比較してロスのVariableを返すようになります。**ロス関数として何を用いるかはデフォルトではF.softmax_cross_entropyとなっていますが、L.Classifierの引数lossfuncにロス計算を行う関数を渡してやれば変更することができるため、Classifierという名前ながら回帰問題などのロス計算機能の追加にも使うことができます。(L.Classifier(net, lossfun=F.mean_squared_error, compute_accuracy=False)のようにする)
StandardUpdaterは前述のようなUpdaterの担当する処理を遂行するための最もシンプルなクラスです。この他にも複数のGPUを用いるためのParallelUpdaterなどが用意されています。
3. Trainerの準備
実際に学習ループ部分を隠蔽しているのはUpdaterなので、これがあればもう学習を始められそうですが、TrainerはさらにUpdaterを受け取って学習全体の管理を行う機能を提供しています。例えば、データセットを何周したら学習を終了するか(stop_trigger) や、途中のロスの値をどのファイルに保存したいか、ロスカーブを可視化した画像ファイルを保存するかどうかなど、学習全体の設定として必須・もしくはあると便利な色々な機能を提供しています。
必須なものとしては学習終了のタイミングを指定するstop_triggerがありますが、これはTrainerオブジェクトを作成するときのコンストラクタで指定します。指定の方法は単純で、(長さ, 単位)という形のタプルを与えればよいだけです。「長さ」には数字を、「単位」には'iteration'もしくは'epoch'のいずれかの文字列を指定します。こうすると、たとえば100 epoch(データセット100周)で学習を終了してください、とか、1000 iteration(1000回更新)で学習を終了してください、といったことが指定できます。Trainerを作るときに、stop_triggerを指定しないと、学習は自動的には止まりません。
では、実際にTrainerオブジェクトを作ってみましょう。
max_epoch = 10
# TrainerにUpdaterを渡す
trainer = training.Trainer(
updater, (max_epoch, 'epoch'), out='mnist_result')
out引数では、この次に説明するExtensionを使って、ログファイルやロスの変化の過程を描画したグラフの画像ファイルなどを保存するディレクトリを指定しています。
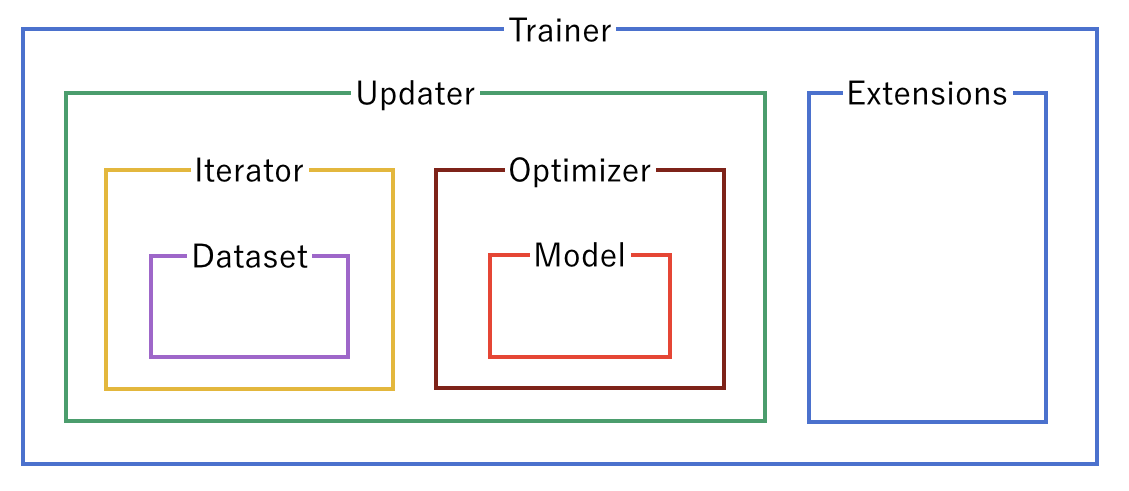
Trainerと、その内側にあるいろいろなオブジェクトの関係は、図にまとめると以下のようになっています。このイメージを持っておくと自分で部分的に改造したりする際に便利だと思います。
4. TrainerにExtensionを追加する
Trainerを使う利点として、
- ログを自動的にファイルに保存(
LogReport) - ターミナルに定期的にロスなどの情報を表示(
PrintReport) - ロスを定期的にグラフで可視化して画像として保存(
PlotReport) - 定期的にモデルやOptimizerの状態を自動シリアライズ(
snapshot) - 学習の進捗を示すプログレスバーを表示(
ProgressBar) - ネットワークの構造をGraphvizのdot形式で保存(
dump_graph) - ネットワークのパラメータの平均や分散などの統計情報を出力(
ParameterStatistics)
などなどの様々な便利な機能を簡単に利用することができる点があります。これらの機能を利用するには、Trainerオブジェクトに対してextendメソッドを使って追加したいExtensionのオブジェクトを渡してやるだけです。では実際に幾つかのExtensionを追加してみましょう。
from chainer.training import extensions
trainer.extend(extensions.LogReport())
trainer.extend(extensions.snapshot(filename='snapshot_epoch-{.updater.epoch}'))
trainer.extend(extensions.Evaluator(valid_iter, net, device=gpu_id), name='val')
trainer.extend(extensions.PrintReport(['epoch', 'main/loss', 'main/accuracy', 'val/main/loss', 'val/main/accuracy', 'l1/W/data/std', 'elapsed_time']))
trainer.extend(extensions.ParameterStatistics(net.predictor.l1, {'std': np.std}))
trainer.extend(extensions.PlotReport(['l1/W/data/std'], x_key='epoch', file_name='std.png'))
trainer.extend(extensions.PlotReport(['main/loss', 'val/main/loss'], x_key='epoch', file_name='loss.png'))
trainer.extend(extensions.PlotReport(['main/accuracy', 'val/main/accuracy'], x_key='epoch', file_name='accuracy.png'))
trainer.extend(extensions.dump_graph('main/loss'))
LogReport
epochやiterationごとのloss, accuracyなどを自動的に集計し、Trainerのout引数で指定した出力ディレクトリにlogというファイル名で保存します。
snapshot
Trainerのout引数で指定した出力ディレクトリにTrainerオブジェクトを指定されたタイミング(デフォルトでは1エポックごと)に保存します。Trainerオブジェクトは上述のようにUpdaterを持っており、この中にOptimizerとモデルが保持されているため、このExtensionでスナップショットをとっておけば、学習の復帰や学習済みモデルを使った推論などが学習終了後にも可能になります。
dump_graph
指定されたVariableオブジェクトから辿れる計算グラフをGraphvizのdot形式で保存します。保存先はTrainerのout引数で指定した出力ディレクトリです。
Evaluator
評価用のデータセットのIteratorと、学習に使うモデルのオブジェクトを渡しておくことで、学習中のモデルを指定されたタイミングで評価用データセットを用いて評価します。内部では、chainer.config.using_config('train', False)が自動的に行われます。backprop_enableをFalseにすることは行われないため、メモリ使用効率はデフォルトでは最適ではありませんが、基本的にはEvaluatorを使えば評価を行うという点において問題はありません。
PrintReport
Reporterによって集計された値を標準出力に出力します。このときどの値を出力するかを、リストの形で与えます。
PlotReport
引数のリストで指定された値の変遷をmatplotlibライブラリを使ってグラフに描画し、出力ディレクトリにfile_name引数で指定されたファイル名で画像として保存します。
ParameterStatistics
指定したレイヤ(Link)が持つパラメータの平均・分散・最小値・最大値などなどの統計情報を計算して、ログに保存します。パラメータが発散していないかなどをチェックするのに便利です。
これらのExtensionは、ここで紹介した以外にも、例えばtriggerによって個別に作動するタイミングを指定できるなどのいくつかのオプションを持っており、より柔軟に組み合わせることができます。詳しくは公式のドキュメントを見てください
5. 学習を開始する
学習を開始するには、Trainerオブジェクトのメソッドrunを呼ぶだけです!
trainer.run()
epoch main/loss main/accuracy val/main/loss val/main/accuracy l1/W/data/std elapsed_time
1 1.6691 0.599884 0.93909 0.805182 0.0359232 2.04951
2 0.672972 0.843211 0.518216 0.866891 0.0366046 4.94805
3 0.459943 0.878826 0.415205 0.88657 0.0370376 7.98442
4 0.389622 0.893163 0.368696 0.896756 0.0372996 10.9229
5 0.353016 0.900895 0.341141 0.904173 0.0374883 13.7746
6 0.329993 0.907171 0.324052 0.907733 0.0376418 16.5909
7 0.31232 0.911065 0.307601 0.912876 0.037766 20.3998
8 0.298098 0.914383 0.294673 0.917128 0.0378814 24.4631
9 0.28597 0.918059 0.283434 0.918414 0.0379859 27.2953
10 0.275202 0.920836 0.273564 0.921479 0.038085 30.1442
初めに取り組んだ学習ループを自分で書いた場合よりもより短いコードで、リッチなログ情報とともに、下記で表示してみるようなグラフなども作りつつ、同様の結果を得ることができました。1層目の全結合層の重み行列の値の標準偏差が、学習の進行とともに徐々に大きくなっていっているのも見て取れて、面白いですね。
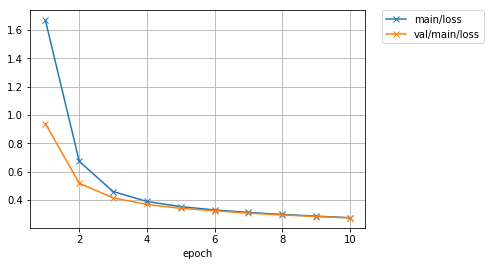
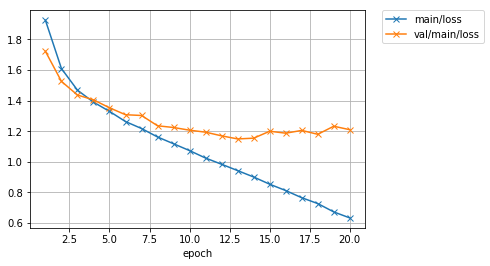
では、保存されているロスのグラフを確認してみましょう。
from IPython.display import Image
Image(filename='mnist_result/loss.png')
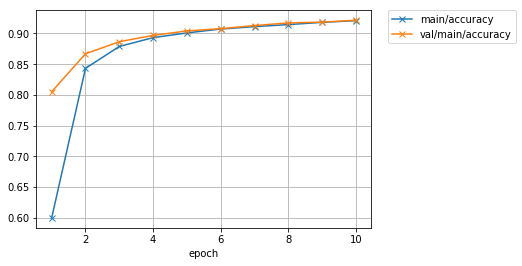
精度のグラフも見てみましょう。
Image(filename='mnist_result/accuracy.png')
もう少し学習を続ければ、まだ多少精度の向上が図れそうな雰囲気がありますね。
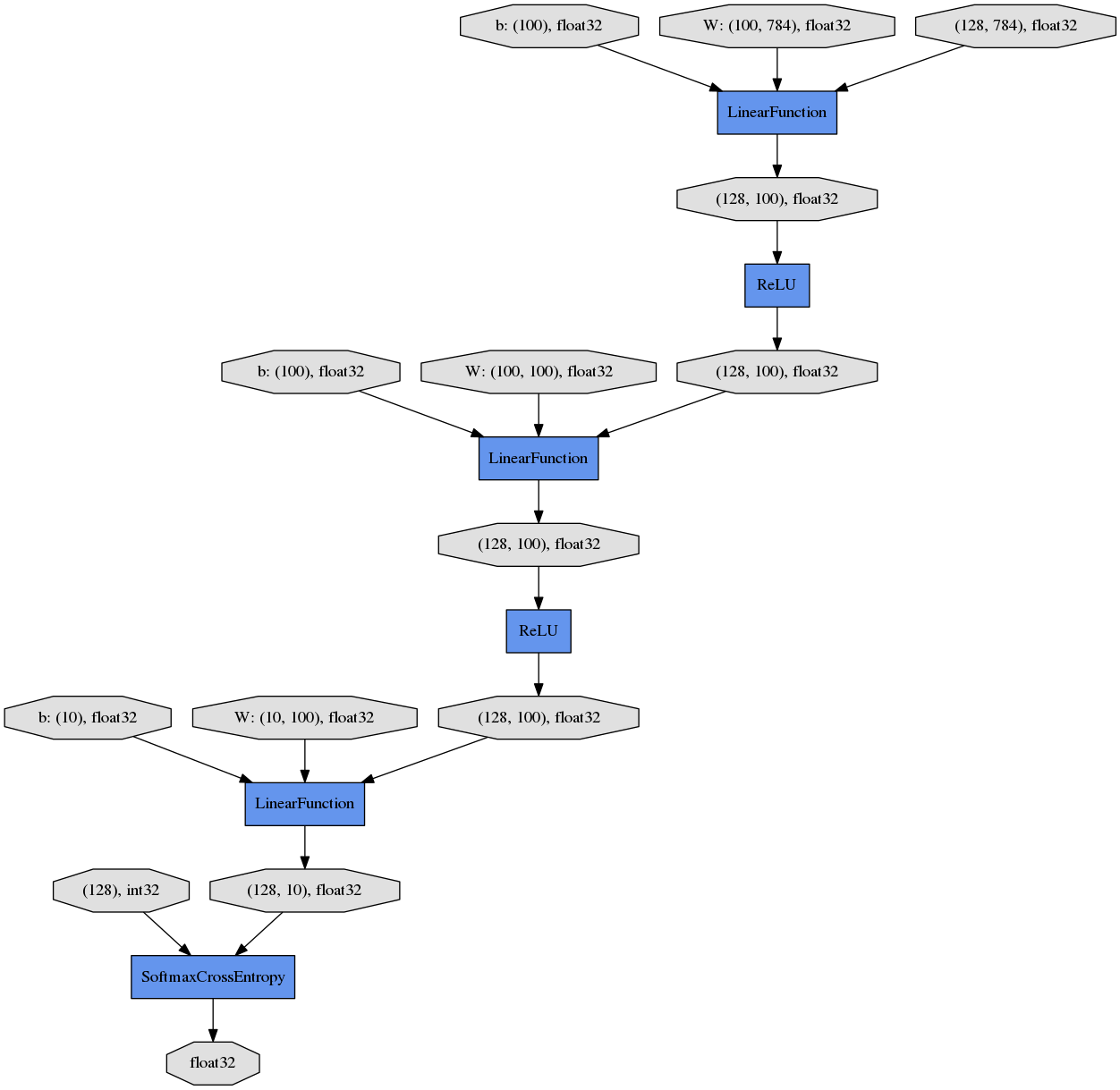
ついでに、dump_graphというExtensionが出力した計算グラフを、Graphvizを使って画像化して見てみましょう。
%%bash
dot -Tpng mnist_result/cg.dot -o mnist_result/cg.png
Image(filename='mnist_result/cg.png')
上から下へ向かって、データやパラメータがどのようなFunctionに渡されて計算が行われ、ロスを表すVariableが出力されたかが分かります。
6. テストデータで評価する
上でもValidationデータに対しての評価を学習中に行うために使用されているTrainer Extensionの一つであるEvaluatorは、Trainerと関係なく独立して使うこともできます。以下のようにしてIteratorとネットワークのオブジェクト(net)、使用するデバイスIDを渡してEvaluatorオブジェクトを作成し、これを関数として実行するだけです。
test_evaluator = extensions.Evaluator(test_iter, net, device=gpu_id)
results = test_evaluator()
print('Test accuracy:', results['main/accuracy'])
Test accuracy: 0.9257318
7. 学習済みモデルで推論する
それでは、Trainer Extensionのsnapshotが自動的に保存したネットワークのスナップショットから学習済みパラメータを読み込んで、学習ループを書いて学習したときと同様に1番目のテストデータで推論を行ってみましょう。
ここで注意すべきは、snapshotが保存するnpzファイルはTrainer全体のスナップショットであるため、extensionの内部のパラメータなども一緒に保存されています。これは、学習自体を再開するために必要だからです。しかし、今回はネットワークのパラメータだけを読み込めば良いので、serializers.load_npz()のpath引数にネットワーク部分までのパス(updater/model:main/predictor/)を指定しています。こうすることで、ネットワークのオブジェクトにパラメータだけを読み込むことができます。
reset_seed(0)
infer_net = MLP()
serializers.load_npz(
'mnist_result/snapshot_epoch-10',
infer_net, path='updater/model:main/predictor/')
if gpu_id >= 0:
infer_net.to_gpu(gpu_id)
x, t = test[0]
plt.imshow(x.reshape(28, 28), cmap='gray')
plt.show()
x = infer_net.xp.asarray(x[None, ...])
with chainer.using_config('train', False), chainer.using_config('enable_backprop', False):
y = infer_net(x)
y = to_cpu(y.array)
print('予測ラベル:', y.argmax(axis=1)[0])
予測ラベル: 7
無事正解できていますね。
新しいネットワークを書いてみよう
ここでは、MNISTデータセットではなくCIFAR10という32x32サイズの小さなカラー画像に10クラスのいずれかのラベルがついたデータセットを用いて、いろいろなモデルを自分で書いて試行錯誤する流れを体験してみます。
| airplane | automobile | bird | cat | deer | dog | frog | horse | ship | truck |
|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
1. ネットワークの定義
ここでは、さきほど試した全結合層だけからなるネットワークではなく、畳込み層を持つネットワークを定義してみます。3つの畳み込み層を持ち、2つの全結合層がそのあとに続いています。
class MyNet(chainer.Chain):
def __init__(self, n_out):
super(MyNet, self).__init__()
with self.init_scope():
self.conv1 = L.Convolution2D(None, 32, 3, 3, 1)
self.conv2 = L.Convolution2D(32, 64, 3, 3, 1)
self.conv3 = L.Convolution2D(64, 128, 3, 3, 1)
self.fc4 = L.Linear(None, 1000)
self.fc5 = L.Linear(1000, n_out)
def __call__(self, x):
h = F.relu(self.conv1(x))
h = F.relu(self.conv2(h))
h = F.relu(self.conv3(h))
h = F.relu(self.fc4(h))
h = self.fc5(h)
return h
2. 学習
ここで、あとから別のネットワークも簡単に同じ設定で訓練できるよう、train関数を作っておきます。これは、
- ネットワークのオブジェクト
- バッチサイズ
- 使用するGPU ID
- 学習を終了するエポック数
- データセットオブジェクト
- 学習率の初期値
- 学習率減衰のタイミング
などを渡すと、内部でTrainerを用いて渡されたデータセットを使ってネットワークを訓練し、学習が終了した状態のネットワークを返してくれる関数です。Trainer.run()が終了した後に、テストデータセットを使って評価まで行ってくれます。先程のMNISTでの例と違い、最適化手法にはMomentumSGDを用い、ExponentialShiftというExtentionを使って、指定したタイミングごとに学習率を減衰させるようにしてみます。
また、ここではcifar.get_cifar10()が返す学習用データセットのうち9割のデータをtrain、残りの1割をvalidとして使うようにしています。
このtrain関数を用いて、上で定義したMyModelモデルを訓練してみます。
from chainer.datasets import cifar
def train(network_object, batchsize=128, gpu_id=0, max_epoch=20, train_dataset=None, valid_dataset=None, test_dataset=None, postfix='', base_lr=0.01, lr_decay=None):
# 1. Dataset
if train_dataset is None and valid_dataset is None and test_dataset is None:
train_val, test = cifar.get_cifar10()
train_size = int(len(train_val) * 0.9)
train, valid = split_dataset_random(train_val, train_size, seed=0)
else:
train, valid, test = train_dataset, valid_dataset, test_dataset
# 2. Iterator
train_iter = iterators.MultiprocessIterator(train, batchsize)
valid_iter = iterators.MultiprocessIterator(valid, batchsize, False, False)
# 3. Model
net = L.Classifier(network_object)
# 4. Optimizer
optimizer = optimizers.MomentumSGD(lr=base_lr).setup(net)
optimizer.add_hook(chainer.optimizer.WeightDecay(0.0005))
# 5. Updater
updater = training.StandardUpdater(train_iter, optimizer, device=gpu_id)
# 6. Trainer
trainer = training.Trainer(updater, (max_epoch, 'epoch'), out='{}_cifar10_{}result'.format(network_object.__class__.__name__, postfix))
# 7. Trainer extensions
trainer.extend(extensions.LogReport())
trainer.extend(extensions.observe_lr())
trainer.extend(extensions.Evaluator(valid_iter, net, device=gpu_id), name='val')
trainer.extend(extensions.PrintReport(['epoch', 'main/loss', 'main/accuracy', 'val/main/loss', 'val/main/accuracy', 'elapsed_time', 'lr']))
trainer.extend(extensions.PlotReport(['main/loss', 'val/main/loss'], x_key='epoch', file_name='loss.png'))
trainer.extend(extensions.PlotReport(['main/accuracy', 'val/main/accuracy'], x_key='epoch', file_name='accuracy.png'))
if lr_decay is not None:
trainer.extend(extensions.ExponentialShift('lr', 0.1), trigger=lr_decay)
trainer.run()
del trainer
# 8. Evaluation
test_iter = iterators.MultiprocessIterator(test, batchsize, False, False)
test_evaluator = extensions.Evaluator(test_iter, net, device=gpu_id)
results = test_evaluator()
print('Test accuracy:', results['main/accuracy'])
return net
net = train(MyNet(10), gpu_id=0)
epoch main/loss main/accuracy val/main/loss val/main/accuracy elapsed_time lr
1 1.92566 0.304976 1.72248 0.388672 9.64744 0.01
2 1.60993 0.423584 1.52611 0.470703 17.999 0.01
3 1.46872 0.474114 1.43699 0.495898 26.0586 0.01
4 1.39049 0.502264 1.40534 0.49707 33.2387 0.01
5 1.33 0.524261 1.35359 0.515039 41.7211 0.01
6 1.26348 0.547718 1.30809 0.533594 50.5788 0.01
7 1.2179 0.566618 1.30321 0.541211 59.2517 0.01
8 1.16269 0.587447 1.23584 0.566406 69.3356 0.01
9 1.11824 0.603738 1.22467 0.564258 78.8699 0.01
10 1.07353 0.62017 1.20699 0.572852 89.5009 0.01
11 1.02482 0.636586 1.19412 0.577734 97.487 0.01
12 0.984335 0.652355 1.17003 0.591406 108.51 0.01
13 0.942885 0.666171 1.14992 0.595898 117.591 0.01
14 0.9011 0.681646 1.15492 0.598828 126.562 0.01
15 0.853943 0.698531 1.20026 0.5875 135.419 0.01
16 0.812528 0.713319 1.18745 0.597656 145.828 0.01
17 0.765726 0.73149 1.20555 0.594922 154.648 0.01
18 0.727469 0.74343 1.18027 0.603125 165.423 0.01
19 0.672888 0.764423 1.23294 0.596484 176.338 0.01
20 0.633698 0.776855 1.21022 0.598633 186.021 0.01
Test accuracy: 0.605716
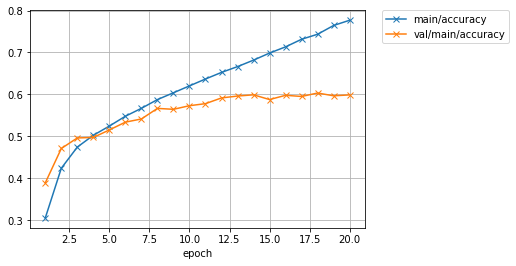
学習が20エポックまで終わりました。ロスと精度のプロットを見てみましょう。
Image(filename='MyNet_cifar10_result/loss.png')
Image(filename='MyNet_cifar10_result/accuracy.png')
学習データでの精度(main/accuracy)は77%程度まで到達していますが、テストデータでのロス(val/main/loss)は途中から下げ止まり、精度(val/main/accuracy)も60%前後で頭打ちになってしまっています。表示されたログの最後の行を見ると、テストデータでの精度も同様に60%程度だったようです。学習データでは良い精度が出ているが、 テストデータでは精度が良くないということなので、モデルが学習データにオーバーフィッティングしていると思われます。
3. 学習済みネットワークを使った予測
テスト精度は60%程度でしたが、試しにこの学習済みネットワークを使っていくつかのテスト画像を分類させてみましょう。あとで使いまわせるようにpredict関数を作っておきます。
cls_names = ['airplane', 'automobile', 'bird', 'cat', 'deer',
'dog', 'frog', 'horse', 'ship', 'truck']
def predict(net, image_id):
_, test = cifar.get_cifar10()
x, t = test[image_id]
net.to_cpu()
with chainer.using_config('train', False), chainer.using_config('enable_backprop', False):
y = net.predictor(x[None, ...]).data.argmax(axis=1)[0]
print('predicted_label:', cls_names[y])
print('answer:', cls_names[t])
plt.imshow(x.transpose(1, 2, 0))
plt.show()
for i in range(10, 15):
predict(net, i)
predicted_label: airplane
answer: airplane
predicted_label: automobile
answer: truck
predicted_label: dog
answer: dog
predicted_label: horse
answer: horse
predicted_label: truck
answer: truck
うまく分類できているものもあれば、そうでないものもありました。ネットワークの学習に使用したデータセット上ではほぼ百発百中で正解できるとしても、未知のデータ、すなわちテストデータセットにある画像に対して高精度な予測ができなければ、意味がありません2。テストデータでの精度は、モデルの汎化性能に関係していると言われます。
どうすれば高い汎化性能を持つネットワークを設計し、学習することができるでしょうか?(そんなことが簡単に分かったら苦労しない。)
4. もっと深いネットワークを定義してみよう
では、上のネットワークよりもよりたくさんの層を持つネットワークを定義してみましょう。ここでは、1層の畳み込みネットワークをConvBlock、1層の全結合ネットワークをLinearBlockとして定義し、これをたくさんシーケンシャルに積み重ねる方法で大きなネットワークを定義してみます。
構成要素を定義する
まず、今目指している大きなネットワークの構成要素となるConvBlockとLinearBlockを定義してみましょう。
class ConvBlock(chainer.Chain):
def __init__(self, n_ch, pool_drop=False):
w = chainer.initializers.HeNormal()
super(ConvBlock, self).__init__()
with self.init_scope():
self.conv = L.Convolution2D(None, n_ch, 3, 1, 1, nobias=True, initialW=w)
self.bn = L.BatchNormalization(n_ch)
self.pool_drop = pool_drop
def __call__(self, x):
h = F.relu(self.bn(self.conv(x)))
if self.pool_drop:
h = F.max_pooling_2d(h, 2, 2)
h = F.dropout(h, ratio=0.25)
return h
class LinearBlock(chainer.Chain):
def __init__(self, drop=False):
w = chainer.initializers.HeNormal()
super(LinearBlock, self).__init__()
with self.init_scope():
self.fc = L.Linear(None, 1024, initialW=w)
self.drop = drop
def __call__(self, x):
h = F.relu(self.fc(x))
if self.drop:
h = F.dropout(h)
return h
ConvBlockはChainを継承した小さなネットワークとして定義されています。これは一つの畳み込み層とBatch Normalization層をパラメータありで持っているので、コンストラクタ内でこれらの登録を行っています。__call__メソッドでは、これらにデータを渡しつつ、活性化関数ReLUを適用して、さらにpool_dropがコンストラクタにTrueで渡されているときはMax PoolingとDropoutという関数を適用するようになっています。
Chainerでは、Pythonを使って書いたforward計算のコード自体がネットワークの構造を表します。すなわち、実行時にデータがどのような層をくぐっていったか、ということがネットワークそのものを定義します。これによって、上記のような分岐などを含むネットワークも簡単に書け、柔軟かつシンプルで可読性の高いネットワーク定義が可能になります。これがDefine-by-Runと呼ばれる特徴です。
大きなネットワークの定義
次に、これらの小さなネットワークを構成要素として積み重ねて、大きなネットワークを定義してみましょう。
class DeepCNN(chainer.ChainList):
def __init__(self, n_output):
super(DeepCNN, self).__init__(
ConvBlock(64),
ConvBlock(64, True),
ConvBlock(128),
ConvBlock(128, True),
ConvBlock(256),
ConvBlock(256),
ConvBlock(256),
ConvBlock(256, True),
LinearBlock(),
LinearBlock(),
L.Linear(None, n_output)
)
def __call__(self, x):
for f in self:
x = f(x)
return x
ここで利用しているのが、ChainListというクラスです。このクラスはChainを継承したクラスで、いくつものLinkやChainを順次呼び出していくようなネットワークを定義するときに便利です。ChainListを継承して定義されるモデルは、親クラスのコンストラクタを呼び出す際にキーワード引数ではなく普通の引数としてLinkもしくはChainオブジェクトを渡すことができます。そしてこれらは、self.children()メソッドによって登録した順番に取り出すことができます。ChainList自体もPythonのイテレータとして機能するので、例えばChainListを継承したクラスの中でfor f in self:...といったことも可能です。
この特徴を使うと、forward計算の記述が簡単になります。self.children()が返す構成要素のリストから、for文で構成要素を順番に取り出していき、そもそもの入力であるxに取り出してきた部分ネットワークの計算を適用して、この出力でxを置き換えるということを順番に行っていけば、一連のLinkまたはChainを、コンストラクタで親クラスに登録した順番と同じ順番で適用していくことができます。そのため、シーケンシャルな部分ネットワークの適用によって表される大きなネットワークを定義するのに重宝します。
それでは、学習を回してみます。今回はパラメータ数も多いので、学習を停止するエポック数を100に設定します。また、学習率を0.1から始めて、30エポックごとに10分の1にするように設定してみます。
TIPS
今回は多くの畳込み層を使う大きなネットワークを使うので、Chainerが用意してくれているcuDNNのautotune機能を有効可してみます。やり方は簡単で、以下の二行を事前に実行しておくだけです。
chainer.cuda.set_max_workspace_size(512 * 1024 * 1024)
chainer.config.autotune = True
それでは、今度こそ学習を開始してみましょう。
reset_seed(0)
model = train(DeepCNN(10), max_epoch=100, base_lr=0.1, lr_decay=(30, 'epoch'))
epoch main/loss main/accuracy val/main/loss val/main/accuracy elapsed_time lr
1 2.66805 0.163374 2.14499 0.189648 19.3804 0.1
2 2.0508 0.237837 2.03172 0.23125 33.5836 0.1
3 1.90109 0.285345 1.81864 0.307617 48.0566 0.1
4 1.74244 0.34608 2.01173 0.273633 64.1632 0.1
5 1.6333 0.389111 1.629 0.397266 79.1679 0.1
6 1.50544 0.4466 1.61811 0.431445 92.7088 0.1
7 1.35314 0.505876 1.606 0.423242 104.438 0.1
8 1.19823 0.567893 1.19526 0.575195 116.22 0.1
9 1.0728 0.618208 1.31838 0.549023 129.618 0.1
10 0.974313 0.655938 1.00564 0.647266 140.631 0.1
11 0.897739 0.686523 0.845641 0.702734 152.881 0.1
12 0.837259 0.709046 0.964008 0.673437 164.286 0.1
13 0.780534 0.732888 1.1975 0.609375 176.39 0.1
14 0.743671 0.745259 0.736362 0.741602 188.494 0.1
15 0.717165 0.757191 0.739799 0.743555 201.239 0.1
16 0.684576 0.76814 0.796289 0.72207 212.544 0.1
17 0.661639 0.778032 0.83021 0.719922 224.69 0.1
18 0.633936 0.785423 1.17993 0.651758 237.316 0.1
19 0.624017 0.790264 0.981198 0.69043 249.088 0.1
20 0.608494 0.794966 0.837451 0.725781 261.854 0.1
21 0.585992 0.803864 1.01166 0.696484 274.849 0.1
22 0.568304 0.810369 0.861089 0.70625 288.799 0.1
23 0.570798 0.810564 1.01788 0.688281 301.476 0.1
24 0.559657 0.811901 0.841228 0.728711 313.685 0.1
25 0.542451 0.819713 0.851603 0.723047 326.528 0.1
26 0.536695 0.823161 0.793133 0.753516 340.287 0.1
27 0.525463 0.824774 0.821281 0.742383 352.561 0.1
28 0.527928 0.824475 0.629371 0.796094 363.692 0.1
29 0.51218 0.830211 0.64138 0.794922 375.972 0.1
30 0.513306 0.830373 0.648403 0.7875 387.832 0.1
31 0.320646 0.891246 0.394016 0.870898 399.874 0.01
32 0.246237 0.916088 0.3797 0.880469 411.885 0.01
33 0.223746 0.924006 0.382387 0.883008 424.689 0.01
34 0.201898 0.930908 0.378948 0.882422 438.225 0.01
35 0.186824 0.93563 0.370399 0.883594 451.346 0.01
36 0.173529 0.940541 0.375686 0.886328 463.98 0.01
37 0.154772 0.946559 0.413009 0.882812 474.836 0.01
38 0.150695 0.947177 0.399807 0.880078 487.226 0.01
39 0.139391 0.951011 0.417676 0.884766 498.364 0.01
40 0.131167 0.954568 0.405573 0.886719 511.015 0.01
41 0.121253 0.958097 0.423057 0.885156 523.911 0.01
42 0.120638 0.957866 0.410141 0.883594 536.018 0.01
43 0.109189 0.961448 0.441353 0.879297 548.274 0.01
44 0.107569 0.961961 0.432192 0.884766 559.796 0.01
45 0.102009 0.964378 0.432181 0.886328 572.656 0.01
46 0.0996161 0.964988 0.443999 0.87793 585.535 0.01
47 0.0932453 0.967041 0.452139 0.881445 597.528 0.01
48 0.0879048 0.969262 0.450908 0.884766 609.156 0.01
49 0.0933322 0.967352 0.452228 0.883008 621.725 0.01
50 0.0883782 0.96895 0.46483 0.880078 634.555 0.01
51 0.0873798 0.969729 0.471411 0.875195 646.78 0.01
52 0.0899555 0.968683 0.464493 0.882617 658.161 0.01
53 0.0848383 0.971221 0.455103 0.882422 669.137 0.01
54 0.0794684 0.972701 0.454608 0.879883 680.626 0.01
55 0.082094 0.971577 0.491964 0.875 693.268 0.01
56 0.0799809 0.972523 0.526578 0.868359 705.112 0.01
57 0.0795879 0.972856 0.538439 0.864844 717.415 0.01
58 0.0773325 0.973357 0.478144 0.871875 730.885 0.01
59 0.075146 0.972945 0.520115 0.872656 743.595 0.01
60 0.0758757 0.973892 0.549528 0.869336 756.815 0.01
61 0.0472821 0.98422 0.440967 0.886133 768.614 0.001
62 0.0299252 0.990362 0.438435 0.890234 779.477 0.001
63 0.0247615 0.99221 0.435327 0.895703 790.3 0.001
64 0.0221926 0.993345 0.441702 0.896875 803.134 0.001
65 0.0204117 0.993586 0.448859 0.895703 815.305 0.001
66 0.0188024 0.994695 0.453645 0.895703 825.476 0.001
67 0.0156325 0.99566 0.462118 0.896289 837.684 0.001
68 0.0161309 0.994984 0.462184 0.897461 850.523 0.001
69 0.0151435 0.995237 0.467102 0.89707 861.725 0.001
70 0.0136216 0.995983 0.469565 0.896875 872.419 0.001
71 0.0140849 0.995682 0.469501 0.897852 883.692 0.001
72 0.0139553 0.995783 0.474553 0.89668 896.62 0.001
73 0.0131952 0.996138 0.481529 0.896094 909.393 0.001
74 0.0142982 0.995526 0.480778 0.898242 922.065 0.001
75 0.0121332 0.996138 0.478623 0.899805 933.689 0.001
76 0.0111401 0.996728 0.482796 0.899805 947.017 0.001
77 0.0105382 0.99676 0.484633 0.894922 960.926 0.001
78 0.00964496 0.997329 0.485977 0.897266 974.333 0.001
79 0.00995056 0.996826 0.497885 0.897852 988.168 0.001
80 0.0108769 0.996661 0.498564 0.898047 1000.01 0.001
81 0.0108558 0.996982 0.495446 0.896094 1011.5 0.001
82 0.0102108 0.996871 0.494618 0.896484 1024.42 0.001
83 0.0106756 0.996617 0.497753 0.89707 1037.54 0.001
84 0.0100215 0.996893 0.501453 0.897461 1049.84 0.001
85 0.00844761 0.997529 0.493311 0.898438 1065.14 0.001
86 0.00905977 0.997448 0.499073 0.895117 1078.29 0.001
87 0.00930665 0.997062 0.508955 0.894727 1090.16 0.001
88 0.00867714 0.997559 0.504844 0.899219 1102.02 0.001
89 0.00861321 0.99727 0.502856 0.898047 1113.88 0.001
90 0.00728278 0.997952 0.506968 0.898633 1125.68 0.001
91 0.00845109 0.997603 0.503209 0.89707 1138.37 0.0001
92 0.00766607 0.997952 0.507215 0.896875 1151.05 0.0001
93 0.00709555 0.997936 0.508333 0.89707 1164.28 0.0001
94 0.00712828 0.997863 0.501388 0.896094 1175.9 0.0001
95 0.00740915 0.998224 0.507065 0.896094 1188.58 0.0001
96 0.00704248 0.997975 0.502469 0.896875 1199.79 0.0001
97 0.00837506 0.997559 0.50369 0.897461 1212.92 0.0001
98 0.00636488 0.998091 0.501123 0.898633 1225.74 0.0001
99 0.00658172 0.99813 0.496533 0.89707 1239.14 0.0001
100 0.00759665 0.997891 0.50088 0.897656 1251.94 0.0001
Test accuracy: 0.9019976
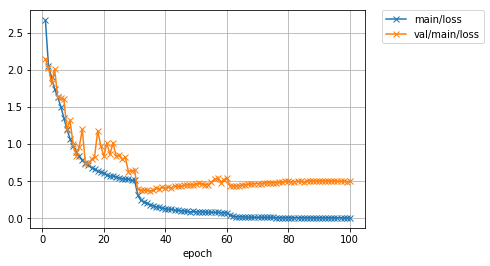
学習が終了しました。ロスカーブと精度のグラフを見てみましょう。
Image(filename='DeepCNN_cifar10_result/loss.png')
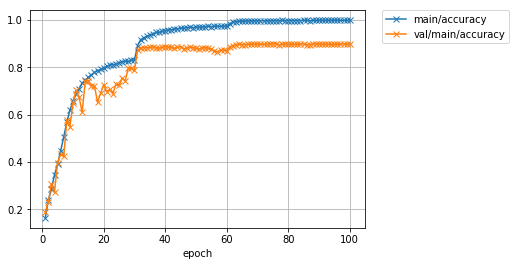
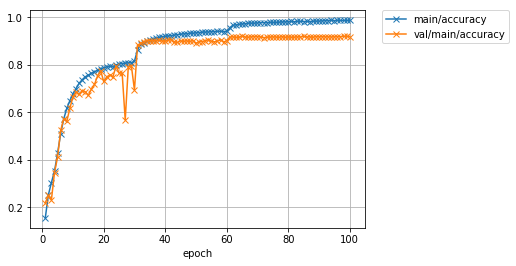
Image(filename='DeepCNN_cifar10_result/accuracy.png')
先程よりも大幅にValidationデータに対する精度が向上したことが分かります。学習率を10分の1に下げるタイミングでロスががくっと減り、精度がガクッと上がっているのが分かります。最終的に、先程60%前後だったValidationデータでの精度が、90%程度まで上がりました。また、テストデータを用いた精度も、およそ90%程度となっています。しかし最新の研究成果では97%以上まで達成されています。さらに精度を上げるには、今回行ったようなネットワークの構造自体の改良ももちろんのこと、学習データを擬似的に増やす操作(Data augmentation)や、複数のモデルの出力を一つの出力に統合する操作(Ensemble)などなど、いろいろな工夫が考えられます。
データセットクラスを書いてみよう
ここでは、Chainerにすでに用意されているCIFAR10のデータを取得する機能を使って、データセットクラスを自分で書いてみます。Chainerでは、データセットを表すクラスは以下の機能を持っていることが必要とされます。
- データセット内のデータ数を返す
__len__メソッド - 引数として渡される
iに対応したデータもしくはデータとラベルの組を返すget_exampleメソッド
その他のデータセットに必要な機能は、chainer.dataset.DatasetMixinクラスを継承することで用意できます。ここでは、DatasetMixinクラスを継承し、Data augmentation機能のついたデータセットクラスを作成してみましょう。
NOTE
自前で用意した、もしくはどこからから調達したラベル付き画像データセットを使う場合は、LabeledImageDatasetというクラスが非常に便利です。詳細はドキュメントを参照してください:LabeledImageDataset。こちらでも使っています:Chainerでアニメキャラクターの顔画像を分類する
1. CIFAR10データセットクラスを書く
class CIFAR10Augmented(chainer.dataset.DatasetMixin):
def __init__(self, split='train', train_ratio=0.9):
train_val, test_data = cifar.get_cifar10()
train_size = int(len(train_val) * train_ratio)
train_data, valid_data = split_dataset_random(train_val, train_size, seed=0)
if split == 'train':
self.data = train_data
elif split == 'valid':
self.data = valid_data
elif split == 'test':
self.data = test_data
else:
raise ValueError("'split' argument should be either 'train', 'valid', or 'test'. But {} was given.".format(split))
self.split = split
self.random_crop = 4
def __len__(self):
return len(self.data)
def get_example(self, i):
x, t = self.data[i]
if self.split == 'train':
x = x.transpose(1, 2, 0)
h, w, _ = x.shape
x_offset = np.random.randint(self.random_crop)
y_offset = np.random.randint(self.random_crop)
x = x[y_offset:y_offset + h - self.random_crop,
x_offset:x_offset + w - self.random_crop]
if np.random.rand() > 0.5:
x = np.fliplr(x)
x = x.transpose(2, 0, 1)
return x, t
このクラスは、CIFAR10のデータのそれぞれに対し、
- 32x32の大きさの中からランダムに28x28の領域をクロップ
- 1/2の確率で左右を反転させる
という加工を行っています。こういった操作を加えることで擬似的に学習データのバリエーションを増やすと、オーバーフィッティングを抑制することに役に立つということが知られています。これらの操作以外にも、画像の色味を変化させるような変換やランダムな回転、アフィン変換など、さまざまな加工によって学習データ数を擬似的に増やす方法が提案されています。
自分でデータの取得部分も書く場合は、コンストラクタに画像フォルダのパスとファイル名に対応したラベルの書かれたテキストファイルへのパスなどを渡してプロパティとして保持しておき、get_exampleメソッド内でそれぞれの画像を読み込んで対応するラベルとともに返す、という風にすれば良いことが分かります。
2. 作成したデータセットクラスを使って学習を行う
それではさっそくこのCIFAR10クラスを使って学習を行ってみましょう。先程使ったのと同じ大きなネットワークを使うことで、Data augmentationの効果がどの程度あるのかを調べてみましょう。train関数も含め、データセットクラス以外は先程とすべて同様です。
reset_seed(0)
model = train(DeepCNN(10), max_epoch=100, train_dataset=CIFAR10Augmented(), valid_dataset=CIFAR10Augmented('valid'), test_dataset=CIFAR10Augmented('test'), postfix='augmented_', base_lr=0.1, lr_decay=(30, 'epoch'))
epoch main/loss main/accuracy val/main/loss val/main/accuracy elapsed_time lr
1 2.66932 0.155096 2.07969 0.218945 17.7946 0.1
2 1.95089 0.252242 2.16529 0.249609 33.6332 0.1
3 1.80029 0.304087 2.41118 0.232617 48.9252 0.1
4 1.68941 0.352428 1.74426 0.346289 64.1672 0.1
5 1.51953 0.427662 1.64889 0.411523 80.7169 0.1
6 1.33687 0.510121 1.33771 0.523438 96.9036 0.1
7 1.19523 0.572338 1.24248 0.573242 113.866 0.1
8 1.08409 0.616544 1.24074 0.562109 129.411 0.1
9 1.0027 0.64917 1.1433 0.617969 146.937 0.1
10 0.929279 0.677974 0.990748 0.664648 163.91 0.1
11 0.872005 0.699929 0.968499 0.68418 181.605 0.1
12 0.8138 0.722111 0.978409 0.675781 199.057 0.1
13 0.778692 0.73746 0.941924 0.691602 215.46 0.1
14 0.748357 0.749332 0.954998 0.686523 233 0.1
15 0.723875 0.757147 1.03263 0.671484 248.429 0.1
16 0.70128 0.763844 0.922967 0.697852 264.35 0.1
17 0.686641 0.770774 0.932868 0.717188 281.515 0.1
18 0.667459 0.777033 0.761607 0.753125 296.919 0.1
19 0.657883 0.783787 0.696336 0.775586 314.209 0.1
20 0.643969 0.787509 0.788956 0.729883 330.866 0.1
21 0.62682 0.791867 0.747854 0.749414 348.447 0.1
22 0.617861 0.793413 0.724289 0.757422 366.256 0.1
23 0.615907 0.792824 0.760725 0.749609 383.692 0.1
24 0.608608 0.799316 0.626627 0.794141 399.339 0.1
25 0.581148 0.804532 0.724842 0.766016 415.612 0.1
26 0.586145 0.805578 0.758912 0.765039 432.683 0.1
27 0.580653 0.806974 1.53115 0.567773 449.495 0.1
28 0.58332 0.808249 0.638048 0.792773 465.692 0.1
29 0.575656 0.809171 0.597601 0.795898 482.273 0.1
30 0.554497 0.815193 0.92648 0.694141 499.854 0.1
31 0.412056 0.862948 0.353921 0.882812 516.331 0.01
32 0.330784 0.886841 0.323626 0.890625 532.822 0.01
33 0.309464 0.893932 0.314378 0.897461 549.781 0.01
34 0.292333 0.900613 0.298411 0.902148 566.772 0.01
35 0.276572 0.904848 0.294187 0.901758 584.074 0.01
36 0.264323 0.909113 0.306759 0.900781 601.223 0.01
37 0.253866 0.913996 0.300004 0.901172 618.957 0.01
38 0.244404 0.915461 0.289046 0.904883 636.233 0.01
39 0.235541 0.918581 0.302103 0.900781 654.649 0.01
40 0.231642 0.919545 0.309698 0.899219 670.247 0.01
41 0.228038 0.921964 0.294209 0.904102 687.482 0.01
42 0.225327 0.923233 0.300517 0.905273 705.459 0.01
43 0.21667 0.925471 0.323513 0.896875 722.654 0.01
44 0.211944 0.927017 0.323403 0.894141 740.125 0.01
45 0.203643 0.92911 0.306549 0.901367 757.691 0.01
46 0.201874 0.930622 0.316553 0.898633 774.53 0.01
47 0.197785 0.93093 0.321795 0.901172 790.748 0.01
48 0.19062 0.933872 0.326009 0.898438 807.37 0.01
49 0.189966 0.932994 0.302136 0.902148 823.616 0.01
50 0.188014 0.934792 0.351239 0.89082 841.241 0.01
51 0.182187 0.935764 0.330658 0.897461 859.206 0.01
52 0.180877 0.937744 0.331513 0.898242 875.571 0.01
53 0.177914 0.937967 0.315606 0.900977 892.888 0.01
54 0.177183 0.938565 0.30771 0.906055 909.576 0.01
55 0.172863 0.939815 0.310448 0.899414 926.626 0.01
56 0.171187 0.940252 0.334125 0.896875 943.697 0.01
57 0.17084 0.941251 0.321309 0.900586 960.606 0.01
58 0.166495 0.941462 0.313928 0.905078 977.788 0.01
59 0.170402 0.94043 0.336456 0.896094 994.226 0.01
60 0.165143 0.941306 0.333355 0.901758 1011.56 0.01
61 0.125434 0.95641 0.277837 0.916797 1028.05 0.001
62 0.0972963 0.967036 0.279862 0.918164 1044.82 0.001
63 0.0909571 0.968373 0.281997 0.915625 1063.31 0.001
64 0.0854286 0.970197 0.279891 0.916406 1078.31 0.001
65 0.0803817 0.972368 0.283583 0.921484 1094.7 0.001
66 0.078539 0.972945 0.277332 0.917383 1111.61 0.001
67 0.0718806 0.975539 0.289384 0.916406 1128.09 0.001
68 0.0706877 0.975608 0.289274 0.917969 1145.55 0.001
69 0.0701198 0.975405 0.287858 0.91875 1161.81 0.001
70 0.0672646 0.976562 0.289723 0.918555 1178.87 0.001
71 0.0635346 0.978009 0.293459 0.917773 1196.21 0.001
72 0.0641605 0.977583 0.296556 0.914258 1213.21 0.001
73 0.0624464 0.978094 0.297749 0.916406 1229.1 0.001
74 0.0622282 0.978543 0.29798 0.916797 1245.15 0.001
75 0.0624434 0.978538 0.302791 0.917578 1261.09 0.001
76 0.062236 0.978655 0.303235 0.917383 1278.4 0.001
77 0.0583369 0.979759 0.294987 0.91582 1295.95 0.001
78 0.0563044 0.980725 0.30498 0.91875 1310.97 0.001
79 0.0551139 0.980846 0.304319 0.91582 1327.2 0.001
80 0.0538306 0.981548 0.301928 0.917578 1343.2 0.001
81 0.0498568 0.982599 0.303399 0.916406 1359.95 0.001
82 0.0522237 0.981845 0.306208 0.916602 1377.32 0.001
83 0.0487175 0.983284 0.307845 0.917773 1392.65 0.001
84 0.0507888 0.982622 0.305499 0.917383 1409.53 0.001
85 0.0502483 0.982394 0.309835 0.919727 1425.66 0.001
86 0.0495274 0.983043 0.313392 0.917578 1441.89 0.001
87 0.0492812 0.982594 0.308399 0.917969 1458.86 0.001
88 0.0467606 0.983643 0.317299 0.916211 1476.23 0.001
89 0.0451622 0.984042 0.320555 0.918945 1493.84 0.001
90 0.0457013 0.984197 0.313627 0.917773 1510.37 0.001
91 0.0436299 0.984952 0.311594 0.91875 1527.8 0.0001
92 0.0405673 0.986178 0.311017 0.917773 1545.44 0.0001
93 0.0399707 0.986306 0.313432 0.917969 1562.86 0.0001
94 0.0375223 0.987892 0.313193 0.917578 1580.18 0.0001
95 0.0403957 0.986461 0.3141 0.917969 1594.47 0.0001
96 0.0385853 0.987024 0.311208 0.918555 1610.3 0.0001
97 0.0380802 0.986972 0.309954 0.918359 1628.06 0.0001
98 0.0383922 0.986994 0.311925 0.920117 1644.28 0.0001
99 0.0389155 0.986979 0.309176 0.919727 1660.87 0.0001
100 0.0371039 0.98766 0.311089 0.919141 1676.64 0.0001
Test accuracy: 0.9186115
先程のData augmentationなしの場合は90%程度だったテスト精度が、学習データにaugmentationを施すことで92%程度まで向上させられることが分かりました。およそ2%の改善です。
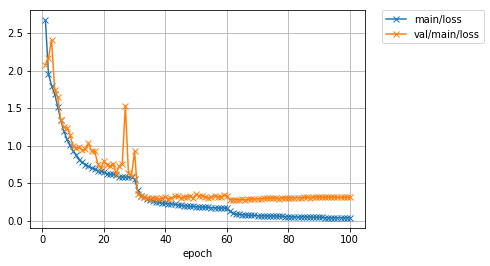
ロスと精度のグラフを見てみましょう。
Image(filename='DeepCNN_cifar10_augmented_result/loss.png')
Image(filename='DeepCNN_cifar10_augmented_result/accuracy.png')
もっと簡単にData Augmentationしよう
前述のようにデータセット内の各画像についていろいろな変換を行って擬似的にデータを増やすような操作をData Augmentationといいます。上では、オリジナルのデータセットクラスを作る方法を示すために変換の操作もget_example()内に書くという実装を行いましたが、実はもっと簡単にいろいろな変換をデータに対して行う方法があります。
それは、TransformDatasetクラスを使う方法です。TransformDatasetは、元になるデータセットオブジェクトと、そこからサンプルしてきた各データ点に対して行いたい変換を関数の形で与えると、変換済みのデータを返してくれるようなデータセットオブジェクトに加工してくれる便利なクラスです。かんたんな使い方は以下です。
from chainer.datasets import TransformDataset
train_val, test_dataset = cifar.get_cifar10()
train_size = int(len(train_val) * 0.9)
train_dataset, valid_dataset = split_dataset_random(train_val, train_size, seed=0)
# 行いたい変換を関数の形で書く
def transform(inputs):
x, t = inputs
x = x.transpose(1, 2, 0)
h, w, _ = x.shape
x_offset = np.random.randint(4)
y_offset = np.random.randint(4)
x = x[y_offset:y_offset + h - 4,
x_offset:x_offset + w - 4]
if np.random.rand() > 0.5:
x = np.fliplr(x)
x = x.transpose(2, 0, 1)
return x, t
# 各データをtransformにくぐらせたものを返すデータセットオブジェクト
train_dataset = TransformDataset(train_dataset, transform)
このようにすると、この新しいtrain_datasetは、上で自分でデータセットクラスごと書いたときと同じような変換を行った上でデータを返してくれるデータセットオブジェクトになります。
ChainerCVでいろいろな変換を簡単に行おう
さて、上では画像に対してランダムクロップと、ランダムに左右反転というのをやりました。もっと色々な変換を行いたい場合、上記のtransform関数に色々な処理を追加していけばよいことになりますが、毎回使いまわすような変換処理をそのたびに書くのは面倒です。何かいいライブラリとか無いのかな、となります。そこでChainerCV[Niitani 2017]です!今年のACM MultimediaのOpen Source Software CompetitionにWebDNN[Hidaka 2017]とともに出場していたChainerにComputer Vision向けの便利な機能を色々追加する補助パッケージ的なオープンソース・ソフトウェアです。
%%bash
pip install chainercv
Requirement already satisfied: chainercv in /home/shunta/.pyenv/versions/anaconda3-5.0.0/lib/python3.6/site-packages
Requirement already satisfied: chainer>=4.0 in /home/shunta/.pyenv/versions/anaconda3-5.0.0/lib/python3.6/site-packages (from chainercv)
Requirement already satisfied: Pillow in /home/shunta/.pyenv/versions/anaconda3-5.0.0/lib/python3.6/site-packages (from chainercv)
Requirement already satisfied: six>=1.9.0 in /home/shunta/.pyenv/versions/anaconda3-5.0.0/lib/python3.6/site-packages (from chainer>=4.0->chainercv)
Requirement already satisfied: numpy>=1.9.0 in /home/shunta/.pyenv/versions/anaconda3-5.0.0/lib/python3.6/site-packages (from chainer>=4.0->chainercv)
Requirement already satisfied: filelock in /home/shunta/.pyenv/versions/anaconda3-5.0.0/lib/python3.6/site-packages (from chainer>=4.0->chainercv)
Requirement already satisfied: protobuf>=3.0.0 in /home/shunta/.pyenv/versions/anaconda3-5.0.0/lib/python3.6/site-packages (from chainer>=4.0->chainercv)
Requirement already satisfied: setuptools in /home/shunta/.pyenv/versions/anaconda3-5.0.0/lib/python3.6/site-packages (from protobuf>=3.0.0->chainer>=4.0->chainercv)
You are using pip version 9.0.1, however version 10.0.1 is available.
You should consider upgrading via the 'pip install --upgrade pip' command.
ChainerCVには、画像に対する様々な変換があらかじめ用意されています。
そのため、上でNumPyを使ってごにょごにょ書いていたランダムクロップやランダム左右反転は、chainercv.transformsモジュールを使うと、それぞれ以下のように1行で書くことができます:
x = transforms.random_crop(x, (28, 28)) # ランダムクロップ
x = chainercv.transforms.random_flip(x) # ランダム左右反転
chainercv.transformsモジュールを使って、transform関数をアップデートしてみましょう。ちなみに、get_cifar10()で得られるデータセットでは、デフォルトで画像の画素値の範囲が[0, 1]にスケールされています。しかし、get_cifar10()にscale=255.を渡しておくと、値の範囲をもともとの[0, 255]のままにできます。今回transformの中で行う処理は、以下の5つです:
- PCA lighting: これは大雑把に言えば、少しだけ色味を変えるような変換です
- Standardization: 訓練用データセット全体からチャンネルごとの画素値の平均・標準偏差を求めて標準化をします
- Random flip: ランダムに画像の左右を反転します
- Random expand:
[1, 1.5]からランダムに決めた大きさの黒いキャンバスを作り、その中のランダムな位置へ画像を配置します - Random crop:
(28, 28)の大きさの領域をランダムにクロップします
from functools import partial
from chainercv import transforms
train_val, test_dataset = cifar.get_cifar10(scale=255.)
train_size = int(len(train_val) * 0.9)
train_dataset, valid_dataset = split_dataset_random(train_val, train_size, seed=0)
mean = np.mean([x for x, _ in train_dataset], axis=(0, 2, 3))
std = np.std([x for x, _ in train_dataset], axis=(0, 2, 3))
def transform(inputs, train=True):
img, label = inputs
img = img.copy()
# Color augmentation
if train:
img = transforms.pca_lighting(img, 76.5)
# Standardization
img -= mean[:, None, None]
img /= std[:, None, None]
# Random flip & crop
if train:
img = transforms.random_flip(img, x_random=True)
img = transforms.random_expand(img, max_ratio=1.5)
img = transforms.random_crop(img, (28, 28))
return img, label
train_dataset = TransformDataset(train_dataset, partial(transform, train=True))
valid_dataset = TransformDataset(valid_dataset, partial(transform, train=False))
test_dataset = TransformDataset(test_dataset, partial(transform, train=False))
ちなみに、pca_lightingは、大雑把にいうと色味を微妙に変えた画像を作ってくれる関数です。
では、standardizationとChainerCVによるPCA Lightingを追加したTransformDatasetを使って学習をしてみましょう。
reset_seed(0)
model = train(DeepCNN(10), max_epoch=100, train_dataset=train_dataset, valid_dataset=valid_dataset, test_dataset=test_dataset, postfix='augmented2_', base_lr=0.1, lr_decay=(30, 'epoch'))
epoch main/loss main/accuracy val/main/loss val/main/accuracy elapsed_time lr
1 2.96298 0.108887 2.28773 0.116992 18.6204 0.1
2 2.28375 0.123069 2.26054 0.145508 35.9189 0.1
3 2.16893 0.173255 1.97104 0.232617 54.1333 0.1
4 1.95599 0.234308 1.96269 0.239453 71.4199 0.1
5 1.84762 0.287482 1.74268 0.316016 89.6395 0.1
6 1.71918 0.344682 1.48986 0.427539 107.843 0.1
7 1.5616 0.420028 1.33444 0.494531 126.049 0.1
8 1.41343 0.48635 1.34962 0.502539 144.103 0.1
9 1.29375 0.542591 1.27011 0.565039 161.386 0.1
10 1.20855 0.577858 1.09895 0.621289 179.561 0.1
11 1.13542 0.603427 1.12695 0.600391 197.048 0.1
12 1.08715 0.626625 0.967723 0.666797 215.84 0.1
13 1.03912 0.645552 1.09458 0.655078 232.916 0.1
14 0.992342 0.661659 0.813403 0.712305 251.279 0.1
15 0.962952 0.676736 0.89199 0.704492 269.464 0.1
16 0.935602 0.687433 0.871531 0.711133 287.93 0.1
17 0.907586 0.694935 0.826585 0.737695 305.05 0.1
18 0.897032 0.699907 0.759569 0.751758 322.843 0.1
19 0.872711 0.70958 0.747807 0.752148 341.134 0.1
20 0.860642 0.710849 0.897129 0.714648 359.493 0.1
21 0.837644 0.720998 0.877011 0.71582 377.873 0.1
22 0.83491 0.719682 0.811209 0.740625 395.061 0.1
23 0.812516 0.730591 0.991357 0.69668 411.923 0.1
24 0.814586 0.728493 0.870199 0.740625 428.436 0.1
25 0.809576 0.730358 0.851287 0.744336 444.849 0.1
26 0.797749 0.73413 1.0621 0.686523 462.494 0.1
27 0.792886 0.737416 0.765583 0.745703 479.124 0.1
28 0.773611 0.74123 0.59921 0.805273 497.053 0.1
29 0.767626 0.742587 1.15419 0.685938 514.952 0.1
30 0.753782 0.749355 0.937311 0.715234 533.238 0.1
31 0.604251 0.797053 0.399113 0.869727 550.994 0.01
32 0.512318 0.827613 0.375138 0.877344 569.219 0.01
33 0.484475 0.834229 0.353442 0.883984 587.753 0.01
34 0.467319 0.841242 0.364244 0.884375 606.206 0.01
35 0.450393 0.846911 0.341441 0.888086 624.712 0.01
36 0.43828 0.848855 0.342883 0.8875 644.334 0.01
37 0.435329 0.851206 0.34381 0.888867 662.547 0.01
38 0.429289 0.852561 0.334433 0.889258 681.356 0.01
39 0.416126 0.857639 0.335736 0.891602 699.445 0.01
40 0.414865 0.857333 0.340546 0.888867 717.644 0.01
41 0.406426 0.85993 0.331028 0.890039 736.169 0.01
42 0.400299 0.864984 0.325277 0.894531 754.238 0.01
43 0.390969 0.863414 0.31114 0.89668 773.074 0.01
44 0.385966 0.867032 0.315048 0.898047 791.369 0.01
45 0.386317 0.868342 0.311667 0.901758 809.057 0.01
46 0.379431 0.869881 0.326095 0.895508 826.949 0.01
47 0.371893 0.871693 0.30523 0.900195 845.462 0.01
48 0.375175 0.869257 0.313753 0.899414 863.334 0.01
49 0.368864 0.872203 0.335674 0.892969 881.266 0.01
50 0.364174 0.874911 0.329148 0.895703 898.805 0.01
51 0.361013 0.876113 0.325556 0.894531 917.536 0.01
52 0.355882 0.876309 0.312672 0.898633 935.827 0.01
53 0.355655 0.877315 0.314614 0.904492 953.22 0.01
54 0.350558 0.878507 0.335558 0.89375 971.412 0.01
55 0.35336 0.879808 0.309912 0.897461 989.554 0.01
56 0.349074 0.878307 0.315572 0.897656 1007.9 0.01
57 0.344636 0.881792 0.315235 0.898633 1026.21 0.01
58 0.351751 0.878361 0.308908 0.90625 1044.43 0.01
59 0.335435 0.885143 0.325415 0.895898 1062.98 0.01
60 0.342543 0.881366 0.307564 0.904492 1081.12 0.01
61 0.296395 0.897061 0.26379 0.914844 1099.85 0.001
62 0.273945 0.905404 0.255291 0.918945 1118 0.001
63 0.256059 0.911111 0.259149 0.918359 1136.27 0.001
64 0.250382 0.913039 0.26012 0.919922 1153.98 0.001
65 0.251402 0.911066 0.252121 0.919922 1172.19 0.001
66 0.246617 0.914795 0.254615 0.917188 1190.44 0.001
67 0.242367 0.916622 0.260114 0.916602 1208.65 0.001
68 0.237993 0.916815 0.251317 0.918359 1227.71 0.001
69 0.233611 0.919627 0.255463 0.92168 1246.66 0.001
70 0.229861 0.920543 0.251819 0.921289 1264.57 0.001
71 0.231212 0.919916 0.256449 0.918359 1282.98 0.001
72 0.230945 0.920388 0.251938 0.922852 1300.6 0.001
73 0.231567 0.918879 0.25467 0.922656 1319.03 0.001
74 0.228168 0.919649 0.25099 0.922266 1336.64 0.001
75 0.223481 0.922452 0.252225 0.921289 1354.76 0.001
76 0.217657 0.923834 0.2558 0.920898 1373.26 0.001
77 0.217563 0.924383 0.247747 0.923828 1392.33 0.001
78 0.216533 0.923722 0.244587 0.923242 1410.24 0.001
79 0.217534 0.924383 0.248184 0.922852 1428.02 0.001
80 0.217936 0.924435 0.245536 0.923828 1446.1 0.001
81 0.213818 0.925448 0.250882 0.921094 1465.16 0.001
82 0.216617 0.924028 0.245679 0.925586 1483.26 0.001
83 0.211348 0.924991 0.252102 0.923242 1502.12 0.001
84 0.21004 0.92658 0.254647 0.919922 1519.85 0.001
85 0.212658 0.926482 0.252338 0.924219 1539.01 0.001
86 0.210038 0.926824 0.256114 0.921094 1556.43 0.001
87 0.209864 0.927885 0.251901 0.921875 1575.17 0.001
88 0.210507 0.926314 0.253217 0.924414 1593.11 0.001
89 0.201081 0.928911 0.254178 0.925195 1610.7 0.001
90 0.207075 0.92873 0.249093 0.922656 1628.39 0.001
91 0.199509 0.929798 0.248616 0.925 1645.72 0.0001
92 0.199114 0.930467 0.250459 0.922266 1664.97 0.0001
93 0.194366 0.932773 0.250289 0.925781 1682.84 0.0001
94 0.192413 0.933605 0.250086 0.921875 1700.81 0.0001
95 0.195286 0.931374 0.25102 0.925977 1719.84 0.0001
96 0.191748 0.932826 0.247356 0.925391 1738.38 0.0001
97 0.188767 0.935258 0.25027 0.924219 1756.14 0.0001
98 0.190619 0.93517 0.249067 0.925 1774.45 0.0001
99 0.190362 0.934206 0.246483 0.925586 1792.49 0.0001
100 0.193294 0.93295 0.247981 0.926172 1810 0.0001
Test accuracy: 0.92108387
わずかに精度が向上しました。他にもネットワークにResNetと呼ばれる有名なアーキテクチャを採用するなど、簡単に試せる改善方法がいくつかあります。ぜひご自分で色々と試してみてください。
おわりに
**Chainerの開発にコミットしてくれる方を歓迎します!**Chainerはオープンソースソフトウェアですので、皆さんが自身で欲しい機能などを提案し、Pull requestを送ることで進化していきます。興味のある方は、こちらのContoribution Guideをお読みになった後、ぜひIssueを立てたりPRを送ったりしてみてください。お待ちしております。
chainer/chainer
https://github.com/chainer/chainer
参考文献
[Tokui 2015] Tokui, S., Oono, K., Hido, S. and Clayton, J., Chainer: a Next-Generation Open Source Framework for Deep Learning, Proceedings of Workshop on Machine Learning Systems(LearningSys) in The Twenty-ninth Annual Conference on Neural Information Processing Systems (NIPS), (2015)
[Niitani 2017] Yusuke Niitani, Toru Ogawa, Shunta Saito, Masaki Saito, "ChainerCV: a Library for Deep Learning in Computer Vision", ACM Multimedia (ACMMM), Open Source Software Competition, 2017
[Hidaka 2017] Masatoshi Hidaka, Yuichiro Kikura, Yoshitaka Ushiku, Tatsuya Harada. WebDNN: Fastest DNN Execution Framework on Web Browser. ACM International Conference on Multimedia (ACMMM), Open Source Software Competition, pp.1213-1216, 2017.