あまり深く考えたくない性格なもので、出来ればざっくりと感覚的に理解したいと常々思っています。
そこで、この損失関数についても、直観的に理解できるように、ちょっと調べてみます。
損失関数ってなによ?
そもそも損失関数ってなんでしょう?
いろいろ調べるとやたら難しい説明が出てきますが、ようは2つの値の差が小さくなるような関数のことのようです。
Deep Learningの識別等では、学習時に、いかに答えに近い値になるように重みパラメータを調整するのかがメインとなるのですが、この「答えに近い値になるように」の部分を担うのが、この「損失関数」というわけです。
「値=損失」ということで、この損失をいかに少なくするのかということで「損失関数」となります。
損失関数の種類
では、損失関数にはどういった種類のものがあるのでしょうか。
ざっと調べてみても、結構な種類があります。
- ヒンジ損失関数
- ε許容誤差関数
- Huber関数
- 指数損失関数
Deep Learningではこういった難しそうなやつではなく、「交差エントロピー誤差」や「二乗誤差」を使用したりします。
重要なのは、この後の処理である「誤差逆伝播」ができる関数であることのようです。
何でなのか、とか、ではどうするのか、などは難しいことが書かれているサイトとかを見ていただくとして、ここではもう上記2つと決めてしまいます。もし勉強するうちに他の関数が出てきたら、こっそり追加します(爆)
交差エントロピー誤差
どう説明しても難しいお話になってしまうので式を載せちゃいますが、一般的にはこんな感じです。
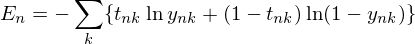
これをTensorFlowで記述するとこうなります。
cross_entropy = tensorflow.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y)
「y_」は正解のラベルで、「y」は学習した結果。この差が小さくなるような処理になります。
なお、比較するにも正規化されてないとまずいということで、「softmax_cross_entropy_with_logits()」の場合は、この中でsoftmaxしているようです。
すでに「y」がsoftmaxで正規化されていれば、こんな感じに書くようです。
cross_entropy = -tensorflow.reduce_sum(y_ * tf.log(y), reduction_indices=[1])
「reduce_sum()」は足し算で、「log()」はそのものズバリで自然対数を求める関数です。
二乗誤差
最小二乗法ってやつも、これのことのようです。
こちらは単純で、差の二乗を求め、それを全クラスで足すだけです。
(その結果が最小になるように調整するイメージ)
TensorFlowでの書き方はいっぱいあるようですが、差の二乗を「tensorflow.nn.reduce_sum()」で加算したり、そもそも「tensorflow.nn.l2_loss()」という関数があったり、二乗も「tensorflow.square()」を使ったり、などなどなど。
まとめ
で、なんか知らないですけど、求めた結果は平均を取るみたいです。
交差エントロピー誤差の場合は、こんな風に書くようです。
cross_entropy = tensorflow.reduce_mean(tensorflow.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
あぁ、次は誤差逆伝播を理解しないと...
