三角関数の加法定理は、
\begin{eqnarray*}
\sin (\alpha + \beta) &=& \sin\alpha\cos\beta + \cos\alpha\sin\beta \\
\cos (\alpha + \beta) &=& \cos\alpha\cos\beta - \sin\alpha\sin\beta
\end{eqnarray*}
などの恒等式である。
$\sin(\alpha - \beta)$ や $\cos(\alpha - \beta)$ に関する公式は、
$\sin (-\beta) = -\sin\beta$ および $\cos(-\beta) = \cos\beta$ から導くことができる。
$\tan$ に関する公式は、この記事では扱わない。
今回は、PDFで用いる座標変換を用いて、この加法定理の式を導いてみる。
PDFで用いる座標変換
PDFに貼る画像の表現方法 #PDF出力 - Qiita
でも紹介したように、PDFでは、以下のような 6 個の数値を引数に取る cm コマンドで座標変換を行うことができる。
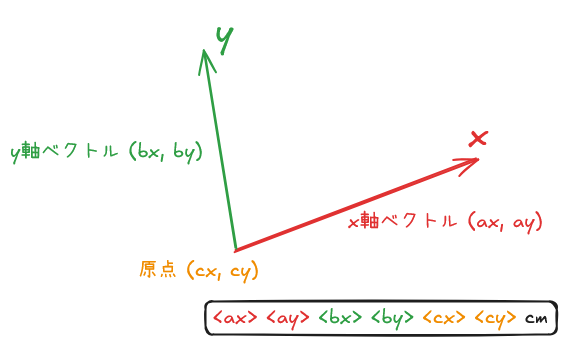
<ax> <ay> <bx> <by> <cx> <cy> cm
これは、
- 新しい座標系で x 軸方向に 1 進むと、現在の座標系で (ax, ay) 進む
- 新しい座標系で y 軸方向に 1 進むと、現在の座標系で (bx, by) 進む
- 新しい座標系の原点は、現在の座標系の (cx, cy)
であることを表している。
三角関数と座標の関係
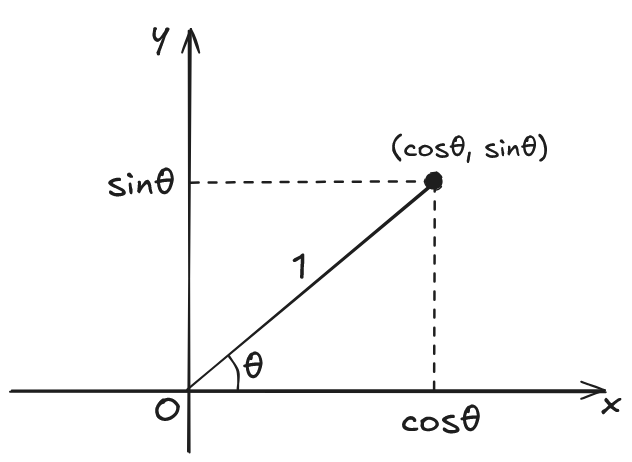
x 軸の正の方向から反時計回りに θ 回した方向に、長さ 1 行った場所の点の座標は、$(\cos \theta, \sin \theta)$ である。
PDFで使う座標変換で、三角関数の加法定理を導く
まず、x 軸と y 軸をそれぞれ原点を中心に $\alpha$ 回転させた座標系を考える。
すると、これは
cosα sinα -sinα cosα 0 0 cm
のように表せるものとなる。
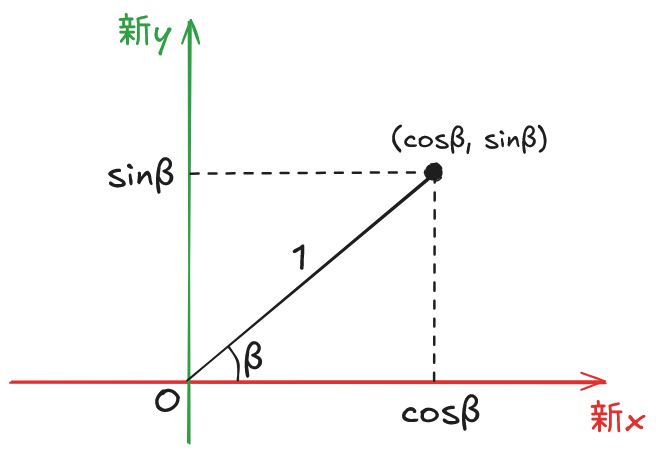
次に、この新しい座標系で、x 軸の正の方向から反時計回りに β 回した方向に、長さ 1 行った場所の点の座標を考えると、これは $(\cos \beta, \sin \beta)$ である。
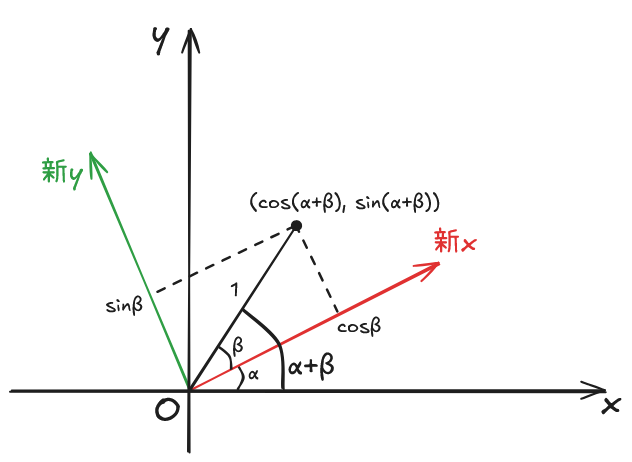
さて、新しい座標系の軸はもとの座標系の軸を $\alpha$ 回転させたものだったので、新しい座標系での点 $(\cos \beta, \sin \beta)$ はもとの座標系では $(\cos (\alpha+\beta), \sin (\alpha+\beta))$ となる。
ここで、今回行った座標変換では
- 新しい座標系の x 軸方向に 1 進むと、もとの座標系では $(\cos \alpha, \sin \alpha)$ 進む
- 新しい座標系の y 軸方向に 1 進むと、もとの座標系では $(-\sin \alpha, \cos \alpha)$ 進む
ことがわかっている。
原点から今考えている点に行くとき、新しい座標系の x 軸方向には $\cos \beta$ 進み、y 軸方向には $\sin \beta$ 進むので、それぞれもとの座標系では
- 新しい座標系の x 軸方向に進んだ分で $(\cos \alpha \cos \beta, \sin \alpha \cos \beta)$ 進む
- 新しい座標系の y 軸方向に進んだ分で $(-\sin \alpha \sin \beta, \cos \alpha \sin \beta)$ 進む
ので、合わせて $(\cos \alpha \cos \beta -\sin \alpha \sin \beta, \sin \alpha \cos \beta + \cos \alpha \sin \beta)$ となる。
一方、この点は $(\cos (\alpha+\beta), \sin (\alpha+\beta))$ だったので、各成分を比較すると
\begin{eqnarray*}
\cos (\alpha+\beta) &=& \cos \alpha \cos \beta -\sin \alpha \sin \beta \\
\sin (\alpha+\beta) &=& \sin \alpha \cos \beta + \cos \alpha \sin \beta
\end{eqnarray*}
だとわかる。
これは、この記事の冒頭で紹介した三角関数の加法定理の式である。
まとめ
PDF で使う座標変換の考え方を用いて、点 $(\cos (\alpha+\beta), \sin (\alpha+\beta))$ の座標を他の表し方で表すことにより、三角関数の加法定理の式を導出することができた。