ベイズ推論を用いた予測では、パラメータの事後分布や予測分布を求める必要があります。尤度関数に対する共役事前分布を用いた線形回帰などのシンプルなモデルでは、事後分布や予測分布を解析的に求めることができます。しかし、ニューラルネットワークなどの複雑な確立モデルでは解析的な推論は困難になります。
観測データを$\mathbf{X}$、パラメータなどの非観測変数の集合を$\mathbf{Z}$としたとき、推論で求めたいのは事後分布$P(\mathbf{Z}|\mathbf{X})$です。今回紹介するサンプリングアルゴリズムは$P(\mathbf{Z}|\mathbf{X})$を明示的に求める代わりに、$P(\mathbf{Z}|\mathbf{X})$からサンプルを採取することで分布の特性を求めます。
この記事では、マルコフ連鎖モンテカルロ法(Markov chain Monte Carlo methods)を用いたいくつかのサンプリングアルゴリズムを解説し、紹介していきます。
※注意
この記事は筆者が勉強したことをまとめて、理解を深めるために執筆しています。内容に誤り等があった場合は、コメント等でご指摘いただけると幸いです。
マルコフ連鎖モンテカルロ法(Markov chain Monte Carlo methods)
一般的なベイズの定理は以下の式で表されます。$\theta$が推定したいパラメータで、$D$が推定に用いることができるデータです。
\begin{aligned}
p\left(\theta | D\right) &=\frac{p\left(D| \theta\right)p(\theta)}{\int p\left(D| \theta\right)p(\theta) d \theta}
\end{aligned}
この計算では、右辺の分母のようにパラメータの積分計算が必要となりますが、しばしばこの積分計算自体が困難な場合があります。右辺の分母を正規化定数と呼びます。
正規化定数を解析的に求めずに事後分布からサンプリングしたい場合に、 マルコフ連鎖モンテカルロ法(Markov chain Monte Carlo methods,以下MCMC法) は有効な手段となります。
MCMC法は、「マルコフ連鎖」と「モンテカルロ法」の組み合わせです。「マルコフ連鎖」や「モンテカルロ法」の理解が怪しい方は、こちらの記事などを参照してください。
確率変数の系列$\mathbf{z}^{(1)},\mathbf{z}^{(2)},\dots$に対して
p(\mathbf{z}^{(t)}|\mathbf{z}^{(1)},\mathbf{z}^{(2)},\dots,\mathbf{z}^{(t-1)})=p(\mathbf{z}^{(t)}|\mathbf{z}^{(t-1)})
が成り立つとき、系列$\mathbf{z}^{(1)},\mathbf{z}^{(2)},\dots$を 一次マルコフ連鎖(first-order Markov Chain) と呼び、$p(\mathbf{z}^{(t)}|\mathbf{z}^{(t-1)})$を 遷移確率 と呼びます。
次式が成り立つとき、分布$p_{*}(\mathbf{z})$は 定常分布 であるといいます。数式の直感的な意味としては、遷移確率に従って事後分布の更新を十分に繰り返したあとに、もう一度遷移確率に従って事後分布を更新しても、分布の様子は変わらない(定常状態)という感じです。
p_{*}(\mathbf{z}) = \int p(\mathbf{z}'|\mathbf{z}) p_{*}(\mathbf{z}') d\mathbf{z}'
定常分布$p_{*}(\mathbf{z})$がサンプルを取り出したい事後分布であるとして、$p(\mathbf{z})$に分布収束するような遷移確率$p(\mathbf{z}^{(t)}|\mathbf{z}^{(t-1)})$を設計するのがMCMC法のアイデアです。
$p_{*}(\mathbf{z})$が定常分布となるための十分条件として、 詳細釣り合い条件(detailed balance condition) があります。
p(\mathbf{z}'|\mathbf{z})p_{*}(\mathbf{z}) = p(\mathbf{z}|\mathbf{z}')p_{*}(\mathbf{z}')
MCMC法が効果を発揮するための数学的な条件としては、詳細釣り合い条件に加えて、サンプルサイズを大きくしたときに遷移確率$p(\mathbf{z}^{(t)}|\mathbf{z}^{(t-1)})$によって任意の初期状態から定常状態$p_{*}(\mathbf{z})$に収束することも必要です。この特性を エルゴード性(ergodicity) と呼びます。
エルゴード性(ergodicity)
- 規約性(irreducible)
- 任意の状態から任意の状態へ有限回数で遷移できること
- 非周期性(aperiodic)
- 全ての状態が周期性を持たないこと
- 正再帰性(positive )
- 全ての状態に有限回で戻ることができること
自己相関係数
相関係数は2つの異なる変数xとyについての相関を見ていますが、自己相関係数は現在の自分と過去の自分でどれだけ相関があるかという係数です。(参考)
\begin{align}
r &= \frac{{cov}(R_{t},R_{t-k})}{\sqrt{V(R_{t})・V(R_{t-k})}} \\
&= \frac{\frac{1}{n}\sum_{n=k+1}^{n}(R_{t}-\bar{R}_{t})(R_{t-k}-\bar{R}_{t})}{\frac{1}{n}\sum_{n=1}^{n}(R_{t}-\bar{R}_t)^2}
\end{align}
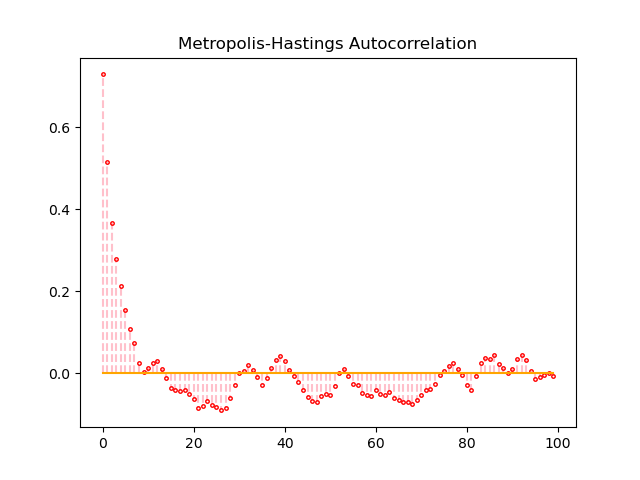
MCMCによるサンプリングが収束しているとき, サンプル列は互いに独立になっています。サンプル列の 自己相関係数 (autocorrelation coefficients) の列をプロットして確認することでMCMCの性能を確認することができます。
良いMCMCでは、自己相関係数が低いため、ラグ=1以降, ラグ次数の増加に伴って自己相関係数の絶対値(現実的にはモンテカルロ法で自己相関係数が完全にゼロになることは少ない)が急速に減少し、ゼロに近い値になるようなサンプルが好ましとされています。
import numpy as np
def autocorrelation(z, k):
z_avg = np.mean(z)
sum_of_covariance = 0
for i in range(k + 1, len(z)):
covariance = (z[i] - z_avg) * (z[i - (k + 1)] - z_avg)
sum_of_covariance += covariance
sum_of_denominator = 0
for u in range(len(z)):
denominator = (z[u] - z_avg)**2
sum_of_denominator += denominator
return sum_of_covariance / sum_of_denominator
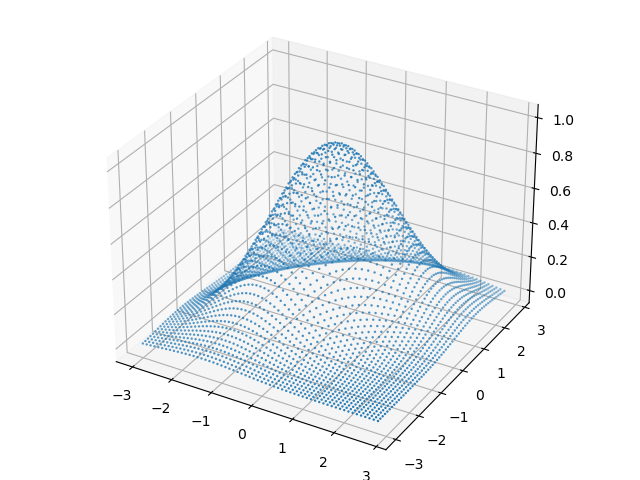
2次元ガウス分布
今回の実験では、得たい目標分布$p(z_1,z_2)$を簡単のため2次元ガウス分布とします。今回の場合では、得たい事後分布から直接サンプリングすることが可能ですが、紹介する3つのアルゴリズムは事後分布が解析的に計算できないときに用いられる手法です。
\mathbf{N}(\boldsymbol{x} | \mu, \Sigma)=\frac{1}{\sqrt{(2 \pi)^{D}|\Sigma|}} \exp \left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}} \Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right\}
$D=2$として平均と分散は次のように設定します。
u=0
\begin{aligned}
\Sigma^{-1}=\left(\begin{array}{cc}
{1} & {-a} \\
{-a} & {1}
\end{array}\right)
\end{aligned}
2次元ガウス分布を3Dプロットすると次図が得られます。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D
a = 0.5
"""
Target distributaion is 2D Gaussian Distribution,
where mu is 0, Sigma^-1 is [1, -a][-a, 1]
P(z1, z2) is target distribution without regulization term.
"""
def P(z1, z2):
return np.exp(-1 / 2 * (z1**2 - 2 * a * z1 * z2 + z2**2))
xs = []
ys = []
zs = []
def range_ex(start, end, step):
while start + step < end:
yield start
start += step
for i in range_ex(-3, 3, 0.1):
for j in range_ex(-3, 3, 0.1):
xs.append(i)
ys.append(j)
zs.append(P(i, j))
ax = Axes3D(plt.figure())
ax.scatter3D(xs, ys, zs, s=3, edgecolor='None')
plt.savefig('gaussian_dist_3d.png')
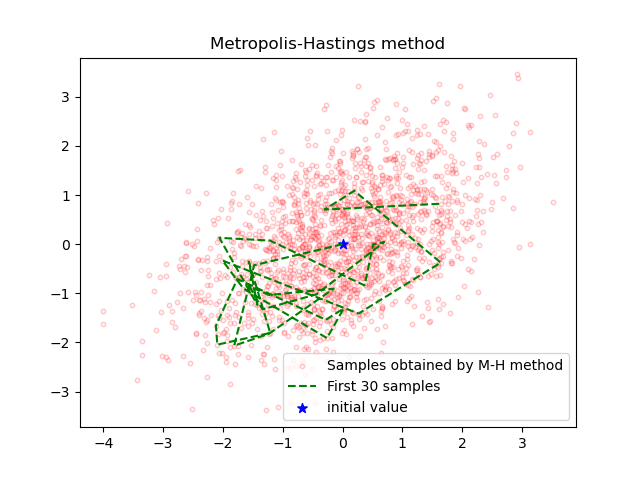
メトロポリス・ヘイスティング法(Metropolis-Hastings method)
MCMC法の最も基本的な手法として、 メトロポリス・ヘイスティングス法(Metropolis-Hastings method,以下M-H法) があります。ベイズの定理において、$\int p\left(D| \theta\right)p(\theta) d \theta$が計算できず、$p\left(D| \theta\right)p(\theta)$が計算可能な場合を想定し、事後分布$p\left(\theta | D\right)$を求めていきます。
\begin{aligned}
p\left(\theta | D\right) &=\frac{p\left(D| \theta\right)p(\theta)}{\int p\left(D| \theta\right)p(\theta) d \theta}
\end{aligned}
MCMC法において、定常分布に収束させるための遷移確率が必要となりますが、遷移確率を直接設計せずに遷移の提案分布$q(\mathbf{z}|\mathbf{z}')$を用います。
重要なのは、サンプリングを試みたい定常分布から直接サンプリングは難しいけれども、提案分布からなら容易にサンプリングが可能という点です。ここで、提案分布により得られた$q(\mathbf{z}|\mathbf{z}')$をの確率で採択することで、詳細つり合い条件を満たすように 棄却サンプリング(rejection sampling) を行おうというのがM-H法のアイデアです。
M-H法を実行してみます。
import copy
import numpy as np
import matplotlib.pyplot as plt
from autocorr import autocorrelation
a = 0.5
# P(z1, z2) is target distribution without regulization term.
def P(z1, z2):
return np.exp(-0.5 * (z1**2 - 2 * a * z1 * z2 + z2**2))
# Q(x) : Proposal distribution
def Q(c, mu1, mu2, sigma):
return (
c[0] +
np.random.normal(
mu1,
sigma),
c[1] +
np.random.normal(
mu2,
sigma))
def metropolis(N, mu1, mu2, sigma):
z = (0, 0)
sample = []
sample.append(z)
accept = []
for i in range(N):
z_new = Q(z, mu1, mu2, sigma)
T_prev = P(z[0], z[1])
T_next = P(z_new[0], z_new[1])
r = T_next / T_prev
if r > 1 or r > np.random.uniform(0, 1):
z = copy.copy(z_new)
sample.append(z)
accept.append(0)
else:
accept.append(1)
rate = np.mean(accept)
print(f'acceptance rate : {rate}')
return np.array(sample)
mu1 = 0
mu2 = 0
sigma = 1
N = 3000
samples = metropolis(N, mu1, mu2, sigma)
# plot scatter
plt.figure()
plt.scatter(samples[:, 0], samples[:, 1], s=10, c='pink', alpha=0.2,
edgecolor='red', label='Samples obtained by M-H method')
plt.plot(samples[0:30, 0], samples[0:30, 1], color='green',
linestyle='dashed', label='First 30 samples')
plt.scatter(samples[0, 0], samples[0, 1], s=50,
c='b', marker='*', label='initial value')
plt.legend(loc=4, prop={'size': 10})
plt.title('Metropolis-Hastings method')
plt.savefig('metropolis.png')
# plot autocorreration graph
acorr_data = []
for i in range(100):
acorr_data.append(autocorrelation(samples, i))
acorr_data = np.asarray(acorr_data)
plt.figure()
markerline, stemlines, baseline = plt.stem(np.arange(
100), acorr_data[0:100, 0], linefmt="--", use_line_collection=True)
markerline.set_color("red")
markerline.set_markerfacecolor("none")
markerline.set_markersize(2.5)
stemlines.set_color("pink")
baseline.set_color("orange")
plt.title('Metropolis-Hastings Autocorrelation')
plt.savefig('metropolis_autocorr.png')
# plot distribution
fig = plt.figure(figsize=(15, 6))
ax = fig.add_subplot(121)
plt.hist(samples[30:, 0], bins=30)
plt.title('x')
ax = fig.add_subplot(122)
plt.hist(samples[30:, 1], bins=30, color="g")
plt.title('y')
plt.savefig('metropolis_dist.png')
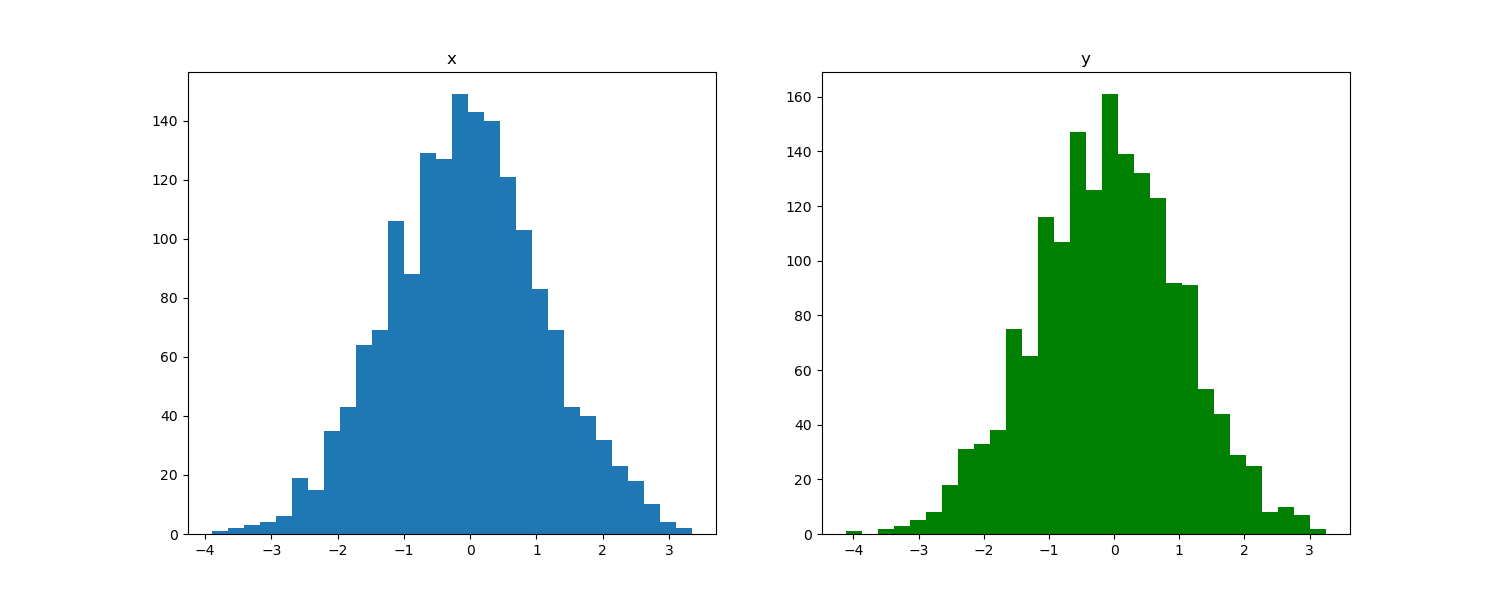
サンプルしたそれぞれの変数の分布は次の図のようになっていました。ガウス分布からサンプリングしてくることに成功しているとみて良いでしょう。
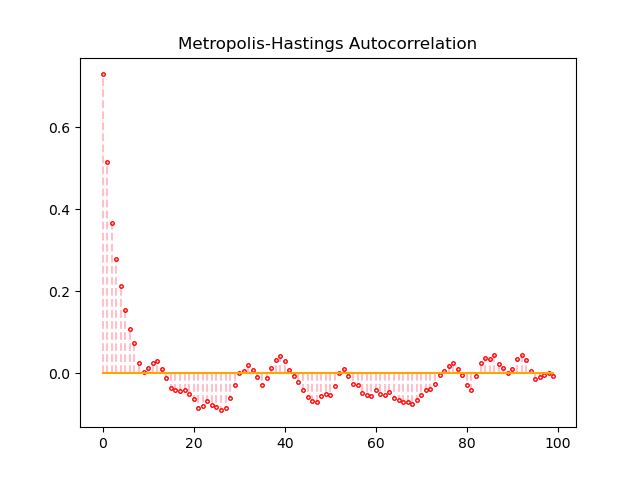
自己相関係数の値は、80回目くらいから0に近い値になっていることが見て取れます。今回の例の場合は、最初の80回のサンプリングはburn-in(慣らし)として破棄するのが好ましいでしょう。
M-H法の受容率(acceptance rate)は0.428でした。
M-H法において、サンプリングしたい事後分布$p(\mathbf{z})$は、問題設定により既に分かっています。提案分布により得られた$q(\mathbf{z}'|\mathbf{z})$は、詳細釣り合い条件を満たすような遷移確率であるとは限りませんので、
q(\mathbf{z}'|\mathbf{z})p(\mathbf{z}) > q(\mathbf{z}|\mathbf{z}')p(\mathbf{z}')
のように等号が成立しているとは限りません。
逆説的に、詳細釣り合い条件を満たすように遷移確率を設定できれば、事後分布$p(\mathbf{z})$からサンプリングできるので、
q(\mathbf{z}'|\mathbf{z})p(\mathbf{z})r = q(\mathbf{z}|\mathbf{z}')p(\mathbf{z}')
のようにある確率$r$で補正を行います。つまり、$\mathbf{z}$から$\mathbf{z}'$へ遷移したとき、それを確率rで採択すれば詳細釣り合い条件が満たされ、$p(\mathbf{z})$からサンプリングができます。
r = \frac{q(\mathbf{z}|\mathbf{z}')p(\mathbf{z}')}{q(\mathbf{z}'|\mathbf{z})p(\mathbf{z})}
$\mathbf{z}$から$\mathbf{z}'$へ遷移したとき、$r>1$となることもありますが、確率が大きく補正されることを意味するので無条件で採択することができます。
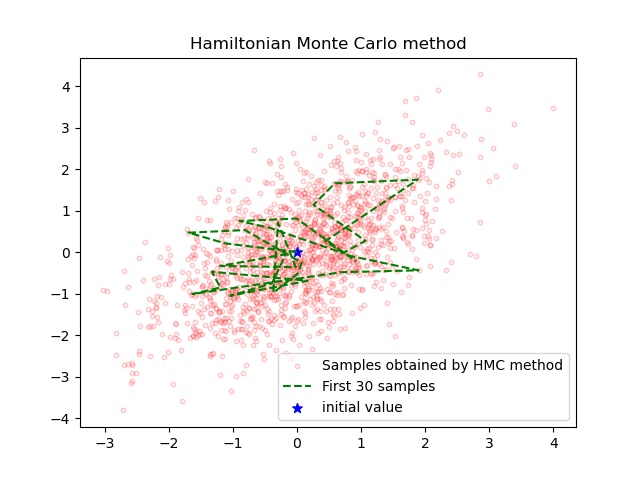
ハミルトニアンモンテカルロ法(Hamiltonian Monte Carlo method)
M-H法には、受容率が低く事後確率に従うサンプルを十分に得られないという課題や前後のサンプルの相関が高く、パラメータ空間を網羅できないといった課題が存在します。そこで、事後分布の微分情報を利用することで、より効率的に事後分布の空間を探索するのが ハミルトニアンモンテカルロ法(Hamiltonian Monte Carlo method,以下HMC法) です。
ハミルトニアン(Hamiltonian)
ハミルトニアン$H(\mathbf{z},\mathbf{p})$は、運動量$\mathbf{p}$を変数に持つ運動エネルギー$K(\mathbf{p})$と位置 $\mathbf{h}$を変数に持つ位置エネルギー$U(\mathbf{z})$を足した物理量です。
H(\mathbf{z},\mathbf{p}) = U(\mathbf{z}) + K(\mathbf{p})
時間$t$によって変化する位置$\mathbf{z}(t)$と、運動量$\mathbf{p}$で表された空間を位相空間と呼びます。簡単のため物体の質量は$1$とし、$K(\mathbf{p})=\frac{1}{2}\mathbf{p}^{T}\mathbf{p}$とします。
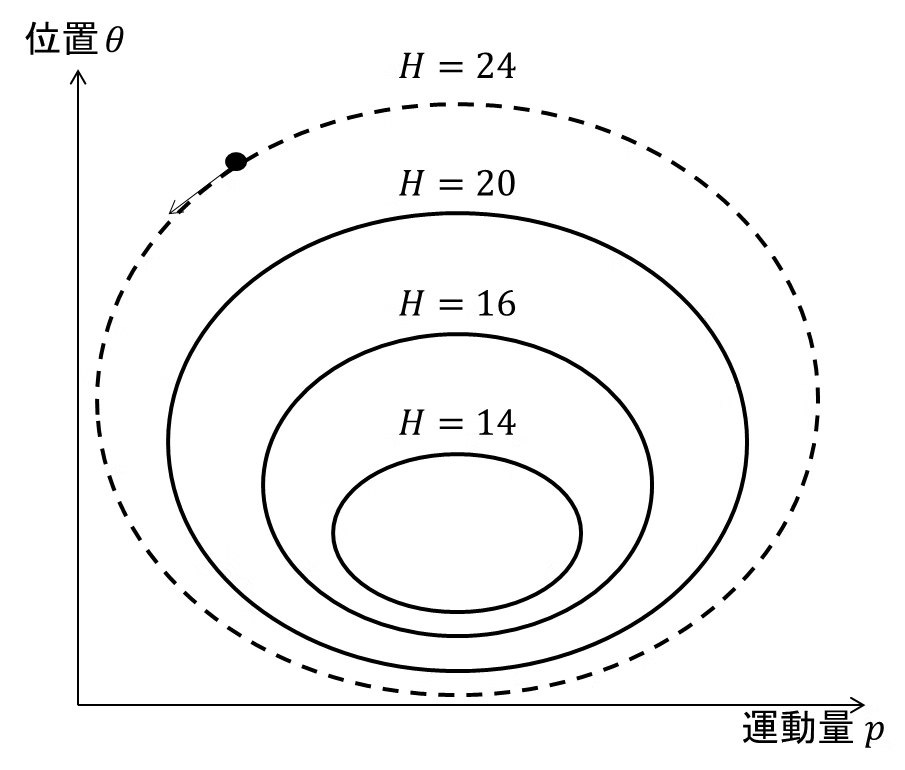
物体はハミルトニアンが一定となるように動き、位相空間で等高線を描くという性質があります。
物体の運動を決めるパラメータである加速度$a(t)$と速度$\mathbf{v}(t)$は、
a(t)=\frac{d\mathbf{p}(t)}{dt} \quad \mathbf{v}(t)=\frac{d\mathbf{z}(t)}{dt}
で表されます。ハミルトニアンが一定であることから、ハミルトニアンを時間$t$で微分すると
\begin{align}
0 &= \frac{dU(\mathbf{z})}{dt} + \frac{K(\mathbf{p})}{dt} \\
&-\frac{dU(\mathbf{z})}{dt} = \frac{K(\mathbf{p})}{dt} \\
&-\frac{dU(\mathbf{z})}{d\mathbf{z}} \frac{d\mathbf{z}}{dt} = \frac{K(\mathbf{p})}{d\mathbf{p}}\frac{d\mathbf{p}}{dt}
\end{align}
従って、ハミルトンの運動方程式は次のように導出できます。
\frac{d\mathbf{p}(t)}{dt}=-\frac{dU(\mathbf{z})}{d\mathbf{z}} \quad \frac{d\mathbf{z}(t)}{dt}=\frac{K(\mathbf{p})}{d\mathbf{p}}
リープフロッグ法(leapfrog method)
ハミルトンの運動方程式から物体の軌道を計算する方法として、 オイラー法(Euler's method) があります。しかしながら、オイラー法で演算誤差が大きいことが知られています。
そこで、運動量$\mathbf{p}(t)$の変化量を$\frac{1}{2}$ステップにして、位置$\mathbf{z}$を高精度に得る リープフロッグ法 が用いられます。
\mathbf{p}(t+\frac{1}{2}) = \mathbf{p}(t) - \frac{dU(\mathbf{z})}{d\mathbf{z}} \frac{1}{2}dt
{\mathbf{z}}(t+1) = {\mathbf{z}}(t) + \mathbf{p}(t+\frac{1}{2}) dt
MHC法によるサンプリング
物体をはじき運動量を与えることを考えると、位相空間において横軸$p$方向に物体は遷移します。このとき、物体をはじくための運動量は標準正規分布でランダムに決定することとすると、物体を弾いたあとの事後確率において運動量$\mathbf{p}$と位置$\mathbf{z}$は独立になります。
サンプルを得たい確率分布$p(\mathbf{z}) \propto p'(\mathbf{z})$と正規化されていない$p'(\mathbf{z})$を考えると、$p(\mathbf{p})=N(\mathbf{p}|\mathbf{0},\mathbf{I})$であり、さらに$\ln{(p'(\mathbf{z}))}=-U(\mathbf{z})$とおくと
\begin{align}
p(\mathbf{z},\mathbf{p})&=p(\mathbf{p})p(\mathbf{z})\\
&=\exp(\ln{(p(\mathbf{z})}+\ln{(p(\mathbf{p})})\\
&\propto\exp(\ln{(p'(\mathbf{z}))}-\frac{1}{2}\mathbf{p}^{T}\mathbf{I}\mathbf{p})\\
&=\exp(-U(\mathbf{z}) - K(\mathbf{p})) \\
&=\exp(-H(\mathbf{z},\mathbf{p}))
\end{align}
となり、ハミルトニアンが得られます。
運動量$\mathbf{p}$をガウス分布に従ってサンプリングしたあと、リープフロッグ法で次の探索点を見つければサンプル点の候補を見つけることができ、このときハミルトニアンは一定に保たれるため
r=\frac{p(\mathbf{z}',\mathbf{p}')}{p(\mathbf{z},\mathbf{p})}=\exp({-H(\mathbf{z}',\mathbf{p}')+H(\mathbf{z},\mathbf{p})})
は常に1に近い値を取ります。実際はリープフロッグ法の誤差の関係で正確な1にはなりませんが、M-H法に比べて高い受託率となります。
import numpy as np
import matplotlib.pyplot as plt
from autocorr import autocorrelation
# Potential energy for the object
def U(z):
return 0.5 * (z[0]**2 - 2 * a * z[0] * z[1] + z[1]**2)
def dU_dz(z):
return (z[0] - a * z[1], z[0] - a * z[1])
# Kinetic energy for the object
def K(p):
return 0.5 * (p[0]**2 + p[1]**2)
def hamiltonian(p, z):
return U(z) + K(p)
def leapfrog_half_p(p, z, eps):
diff = dU_dz(z)
return (p[0] - 0.5 * eps * diff[0], p[1] - 0.5 * eps * diff[1])
def leapfrog_z(p, z, eps):
return (z[0] + eps * p[0], z[1] + eps * p[1])
def hmc_sampler(N, L=100, eps=0.01):
samples = []
accept = []
z = (0, 0)
p = (np.random.normal(0, 1), np.random.normal(0, 1))
prev_H = hamiltonian(p, z)
samples.append(z)
for t in range(N):
z_prev = z
prev_H = hamiltonian(p, z)
for i in range(L):
p = leapfrog_half_p(p, z, eps)
z = leapfrog_z(p, z, eps)
p = leapfrog_half_p(p, z, eps)
H = hamiltonian(p, z)
r = np.exp(prev_H - H)
if r > 1:
samples.append(z)
accept.append(1)
elif r > 0 and np.random.uniform(0, 1) < r:
samples.append(z)
accept.append(1)
else:
z = z_prev
accept.append(0)
p = (np.random.normal(0, 1), np.random.normal(0, 1))
rate = np.mean(accept)
print(f'acceptance rate : {rate}')
return samples
N = 3000
a = 0.5
samples = np.array(hmc_sampler(N))
# plot scatter
plt.figure()
plt.scatter(samples[:, 0], samples[:, 1], s=10, c='pink', alpha=0.2,
edgecolor='red', label='Samples obtained by HMC method')
plt.plot(samples[0:30, 0], samples[0:30, 1], color='green',
linestyle='dashed', label='First 30 samples')
plt.scatter(samples[0, 0], samples[0, 1], s=50,
c='b', marker='*', label='initial value')
plt.legend(loc=4, prop={'size': 10})
plt.title('Hamiltonian Monte Carlo method')
plt.savefig('hmc_sampler.png')
# plot autocorreration graph
acorr_data = []
for i in range(100):
acorr_data.append(autocorrelation(samples, i))
acorr_data = np.asarray(acorr_data)
plt.figure()
markerline, stemlines, baseline = plt.stem(np.arange(
100), acorr_data[0:100, 0], linefmt="--", use_line_collection=True)
markerline.set_color("red")
markerline.set_markerfacecolor("none")
markerline.set_markersize(2.5)
stemlines.set_color("pink")
baseline.set_color("orange")
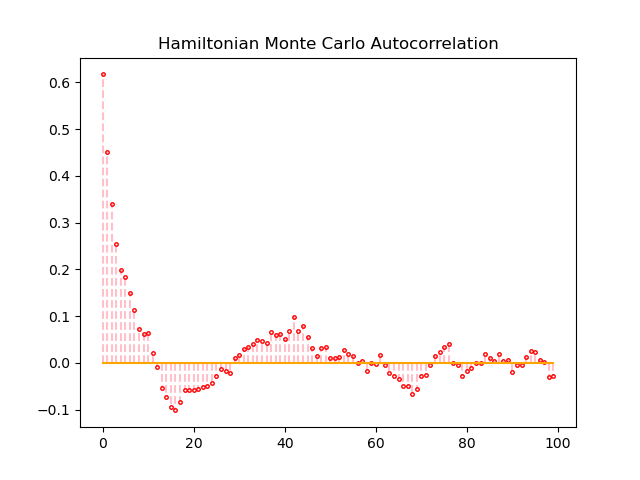
plt.title('Hamiltonian Monte Carlo Autocorrelation')
plt.savefig('hmc_autocorr.png')
# plot distribution
fig = plt.figure(figsize=(15, 6))
ax = fig.add_subplot(121)
plt.hist(samples[30:, 0], bins=30)
plt.title('x')
ax = fig.add_subplot(122)
plt.hist(samples[30:, 1], bins=30, color="g")
plt.title('y')
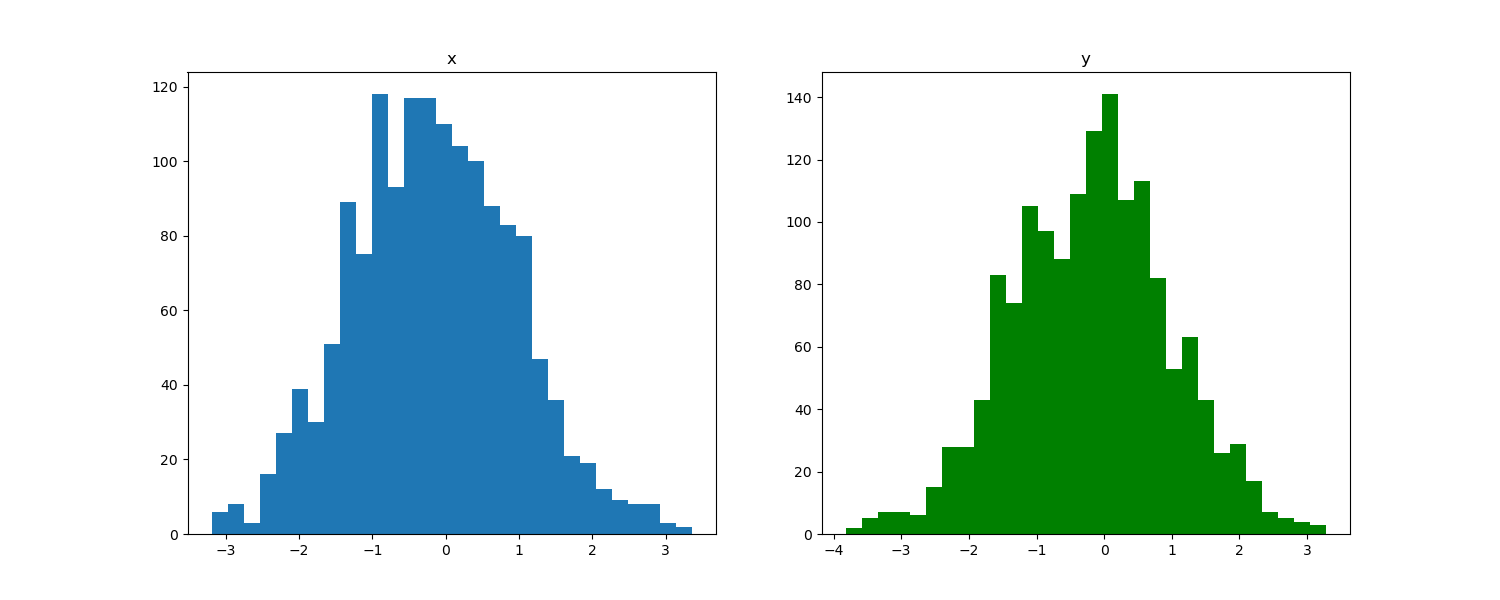
plt.savefig('hmc_dist.png')
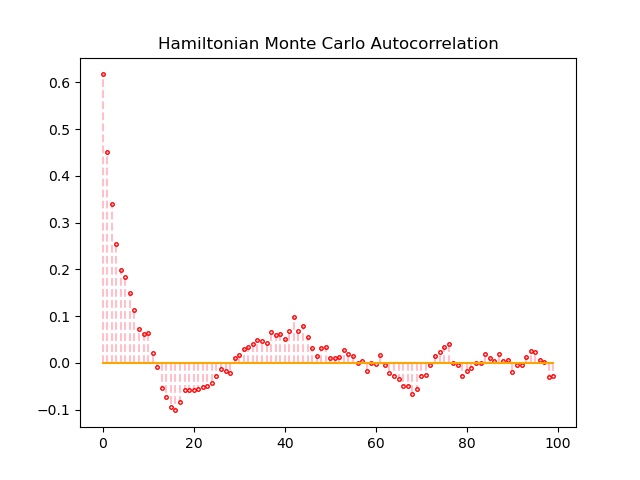
自己相関係数を確認すると、サンプリング回数が50回を超えたあたりから自己相関係数が0に近い値となっていました。
HMC法の受容率は0.529ほどでした。
サンプルしたそれぞれの変数の分布は次の図のようになっていました。こちらも問題なくガウス分布からサンプリングしてくることに成功しています。
ギブスサンプリング(Gibbs Sampling)
確率分布$P(\mathbf{Z})$から直接$\mathbf{Z}$全体をサンプリングすることが難しい場合、$\mathbf{Z}=(\mathbf{Z}_1,\mathbf{Z}_2, \dots ,\mathbf{Z}_M)$のようにM個の部分集合に分けることによって逐次的にサンプリングを行います。
この方法を ギブスサンプリング(Gibbs Sampling) と呼びます。
\mathbf{Z}_1 \sim p(\mathbf{Z}_1|\mathbf{Z}_2,\mathbf{Z}_3, \dots ,\mathbf{Z}_{M-1}, \mathbf{Z}_M) \\
\mathbf{Z}_2 \sim p(\mathbf{Z}_2|\mathbf{Z}_1,\mathbf{Z}_3, \dots ,\mathbf{Z}_{M-1}, \mathbf{Z}_M) \\
\vdots \\
\mathbf{Z}_M \sim p(\mathbf{Z}_M|\mathbf{Z}_1,\mathbf{Z}_2, \dots ,\mathbf{Z}_{M-2}, \mathbf{Z}_{M-1})
ギブスサンプリングはサンプルを得たい変数の数が膨大である場合や、複数の確率分布が組み合わさった巨大な確率モデル化からサンプルを得たい場合に用いられます。
上式の各条件付き分布が解析的に計算できるように共役事前分布をうまく用いてモデルを構築できれば非常に効率的に動作します。
2次元ガウス分布からサンプリング
今回の実験では、得たい目標分布$p(z_1,z_2)$を簡単のため2次元ガウス分布としていました。
\mathbf{N}(\boldsymbol{x} | \mu, \Sigma)=\frac{1}{\sqrt{(2 \pi)^{D}|\Sigma|}} \exp \left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}} \Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right\}
$D=2$として平均と分散は次のように設定しています。
u=0
\begin{aligned}
\Sigma^{-1}=\left(\begin{array}{cc}
{1} & {-a} \\
{-a} & {1}
\end{array}\right)
\end{aligned}
このとき逆行列と行列式は次のように計算できます。
\begin{aligned}
\Sigma = \frac{1}{\left(1-a^{2}\right)}\left(\begin{array}{cc}
{1} & {a} \\
{a} & {1}
\end{array}\right) \\
\end{aligned}
\begin{aligned}
|\Sigma| = \frac{1}{1-a^{2}}
\end{aligned}
従って、目標分布$p(z_1,z_2)$は
\begin{aligned}
&p\left(z_{1}, z_{2}\right) \\
&=\frac{1}{\sqrt{(2 \pi)^{2}|\Sigma|}} \exp \left\{-\frac{1}{2}\left(z_{1}, z_{2}\right) \Sigma^{-1}\left(\begin{array}{c}
{z_{1}} \\
{z_{2}}
\end{array}\right)\right\} \\
&=\frac{\sqrt{1-a^{2}}}{2 \pi} \exp \left\{-\frac{1}{2}\left(z_{1}, z_{2}\right)\left(\begin{array}{cc}
{1} & {-a} \\
{-a} & {1}
\end{array}\right)\left(\begin{array}{c}
{z_{1}} \\
{z_{2}}
\end{array}\right)\right\} \\
&=\frac{\sqrt{1-a^{2}}}{2 \pi} \exp \left\{-\frac{1}{2}\left(z_{1}^{2}-a z_{1} z_{2}-a z_{1} z_{2}+z_{2}^{2}\right)\right\} \\
&=\frac{\sqrt{1-a^{2}}}{2 \pi} \exp \left\{-\frac{1}{2}\left(z_{1}^{2}-2 a z_{1} z_{2}+z_{2}^{2}\right)\right\} \\
&\left.=\frac{\sqrt{1-a^{2}}}{2 \pi} \exp \left\{-\frac{1}{2}\left(1-a^{2}\right) z_{2}^{2}\right\} \exp \left\{-\frac{1}{2}\left(z_{1}-a z_{2}\right)^{2}\right)\right\}
\end{aligned}
と計算できます。最後の行では平方完成を行いました。
今回は簡単な目標分布を設定しているため、$p(z_1,z_2)$からのサンプリングを行うことができますが、ギブスサンプリングを使う場面では$p(\mathbf{Z})$を解析的に計算できないことが多いです。
次に、条件付き確率を導出したいのでベイズの定理を持ちます。
\begin{aligned}
p\left(z_{1} | z_{2}\right) &=\frac{p\left(z_{1}, z_{2}\right)}{p\left(z_{2}\right)} \\
&=\frac{p\left(z_{1}, z_{2}\right)}{\int p\left(z_{1}, z_{2}\right) d z_{1}}
\end{aligned}
ガウス積分の公式を用いて
\begin{aligned}
&\int p\left(z_{1}, z_{2}\right) d x_{1} \\
&\left.=\frac{\sqrt{1-a^{2}}}{2 \pi} \exp \left\{-\frac{1}{2}\left(1-a^{2}\right) z_{2}^{2}\right\} \int \exp \left\{-\frac{1}{2}\left(z_{1}-a z_{2}\right)^{2}\right)\right\} d x_{1} \\
&=\frac{\sqrt{1-a^{2}}}{2 \pi} \exp \left\{-\frac{1}{2}\left(1-a^{2}\right) z_{2}^{2}\right\} \sqrt{2 \pi} \\
&=\sqrt{\frac{1-a^{2}}{2 \pi}} \exp \left\{-\frac{1}{2}\left(1-a^{2}\right) z_{2}^{2}\right\}
\end{aligned}
周辺化ができたので、条件付き確率を求めると
\begin{aligned}
p\left(z_{1} | z_{2}\right) &=\frac{p\left(z_{1}, z_{2}\right)}{\int p\left(z_{1}, z_{2}\right) d z_{1}} \\
&=\frac{\left.\frac{\sqrt{1-a^{2}}}{2 \pi} \exp \left\{-\frac{1}{2}\left(1-a^{2}\right) z_{2}^{2}\right\} \exp \left\{-\frac{1}{2}\left(z_{1}-a z_{2}\right)^{2}\right)\right\}}{\sqrt{\frac{1-a^{2}}{2 \pi}} \exp \left\{-\frac{1}{2}\left(1-a^{2}\right) z_{2}^{2}\right\}} \\
&\left.=\frac{1}{\sqrt{2 \pi}} \exp \left\{-\frac{1}{2}\left(z_{1}-a z_{2}\right)^{2}\right)\right\}
\end{aligned}
となり、条件付き確率は$\mu=az_1$、$\sigma=1$の1次元ガウス分布となりました。
ギブスサンプリングを実行してみます。
import numpy as np
import matplotlib.pyplot as plt
def gibbs_sampler(a, step):
z = np.zeros(2)
samples = z
for i in range(step):
z[0] = np.random.normal(a * z[1], 1)
samples = np.append(samples, (z))
z[1] = np.random.normal(a * z[0], 1)
samples = np.append(samples, (z))
samples = samples.reshape((2 * step + 1, z.shape[0]))
return samples
step = 3000
a = 0.5
samples = gibbs_sampler(a, step)
plt.figure()
plt.scatter(samples[:, 0], samples[:, 1], s=10, c='pink', alpha=0.2,
edgecolor='red', label='Samples obtained by Gibbs Sampling')
plt.plot(samples[0:30, 0], samples[0:30, 1], color='green',
linestyle='dashed', label='First 30 samples')
plt.scatter(samples[0, 0], samples[0, 1], s=50,
c='b', marker='*', label='initial value')
plt.legend(loc=4, prop={'size': 10})
plt.title('Gibbs sampler')
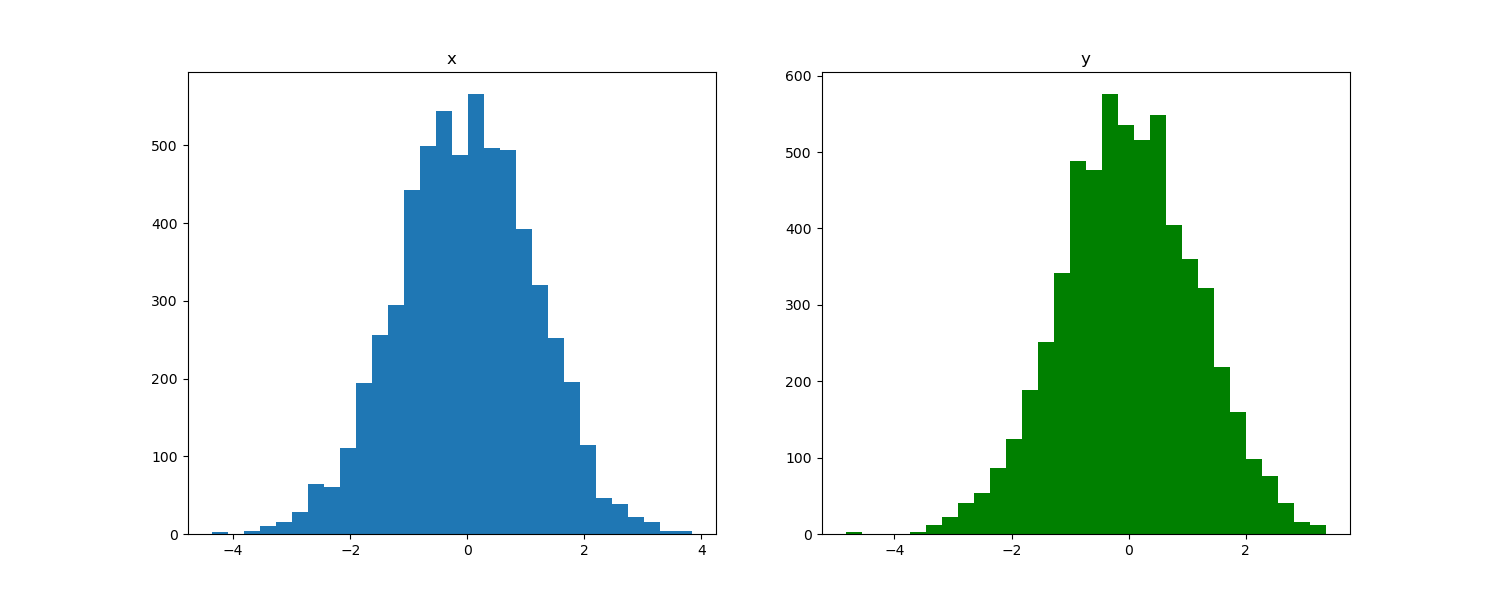
plt.savefig('gibbs_sampler.png')
ギブスサンプリングにおいては、それぞれの変数に対する条件付き分布$p(z_1|z_2)$および$p(z_2|z_1)$を利用してサンプリングを行っているため、得られた軌跡(青い線)は軸に沿った垂直なものになります。
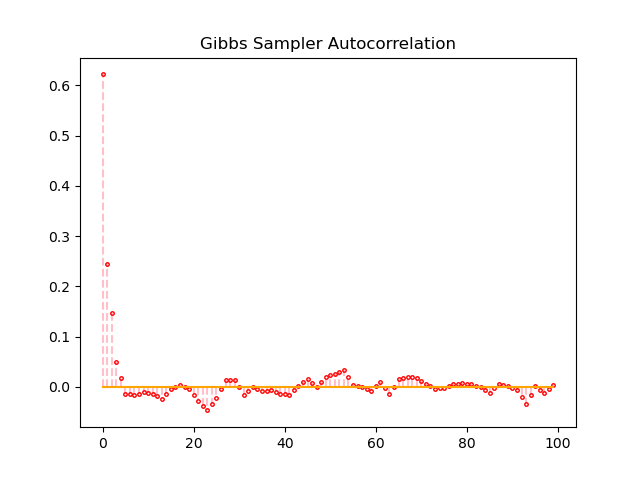
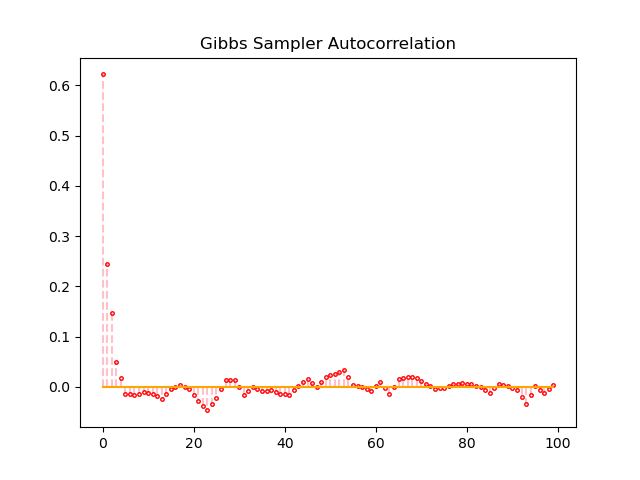
ギブスサンプリングにおける自己相関係数は、サンプリングを開始してすぐに0に近い値に収束しています。
ギブスサンプリングはアルゴリズムの性質上、受容率は100パーセントです。
サンプルしたそれぞれの変数の分布は下図のようになっていました。こちらはガウス分布の形状になっています。
3つのアルゴリズムの比較
M-H法では、提案分布にガウス分布$N(z^t,1)$を用いているため、挙動がランダムウォーク的になって他の二つのアルゴリズムよりも中心に向かっていません。HMC法では、リープフロッグ法の効果によってM-H法よりも積極的に中心に向かっていっているのが図の比較から見て取れます。
| M-H法 | HMC法 | ギブスサンプリング |
|---|---|---|
 |
 |
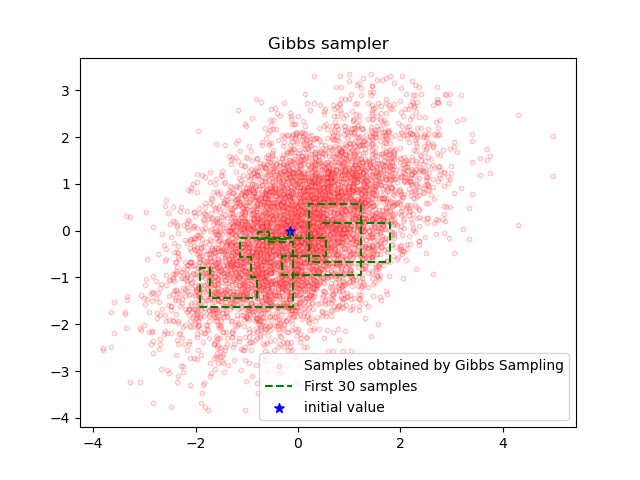 |
また、サンプルの受容率は理論上はM-H法<HMC法<ギブスサンプリングです。今回の実験ではすべて$N=3000$回のサンプルを行っています。少し分かりにくいかもしれませんが、上図ではM-H法よりもHMC法の方が受容されたサンプル点が多いです。実際にM-H法の受容率0.428で、HMC法の受容率は0.529でした。また、ギブスサンプリングでは必ず受容されるので、HMC法よりもギブスサンプリングの方が受容されたサンプル点が多いのは明らかです。
自己相関係数の値に注目すると、ギブスサンプリングにおいて自己相関係数が0へ収束するスピードは、M-H法とHMC-法よりも圧倒的に速いです。MCMCによるサンプリングが収束しているとき, サンプル列は互いに独立になっているため、良いMCMCでは自己相関係数は0に近い値となります。H-M法とHMC法の間では、明確な差は確認できませんでした。
| M-H法 | HMC法 | ギブスサンプリング |
|---|---|---|
 |
 |
 |
まとめ
MCMC法の中でも代表的なM-H法、HMC法、ギブスサンプリングについて調査、比較してみました。個人的に物理学を絡めたMHC法が興味深かったです。
最近はベイズ統計学が流行っている感じがする(?)ので、MCMC法の基礎的な原理やその応用アルゴリズムはしっかりと理解しておきたいです。
今回の実験コードはGitHub上にあります。適宜ご参照ください。
参考
ベイズ深層学習
MCMC入門
【統計学】ハミルトニアンモンテカルロ法をアニメーションで可視化して理解する。
「基礎からのベイズ統計学 -ハミルトニアンモンテカルロ法による実践的入門-」
【MCMC法シリーズその1】MCMC法の概要とメトロポリス法