ハミルトニアンモンテカルロ法(HMC)の動作原理をアニメーションを用いて理解してみようという記事です。
先日の記事、「【統計学】マルコフ連鎖モンテカルロ法(MCMC)によるサンプリングをアニメーションで解説してみる。」の続編にあたります。
豊田先生の書籍「基礎からのベイズ統計学」の例題を使わせていただき、サンプリング対象の分布は今回ガンマ分布とします。本記事ではアニメーションに使った部分の理論的な解説しかしませんので、HMCの詳細な解説はこちらの書籍をご参照いただければと思います。
はじめに
推定する対象は$\theta$を変数としたガンマ分布です。ベイズ推定で推定したいパラメーターを$\theta$で表すので、$\theta$の分布として表されます。1
ガンマ分布はこちらです。
$$ f(\theta|\alpha, \lambda) = {\lambda^{\alpha} \over \Gamma(\alpha)} \theta^{\alpha-1}e^{-\lambda \theta}
\quad \quad 0 \le x,\quad 0 < \lambda,\quad 0 < \alpha $$
このガンマ分布のうち、正規化定数を除いたカーネル部分だけに着目すると、
$$ f(\theta|x) \propto e^{-\lambda \theta} \theta ^{\alpha -1} $$
となります。
HMCではこれにログを取ってマイナスをかけたもの、つまり
$$h(\theta) = -\log (f(\theta|x)) = \lambda \theta - (\alpha -1) \log(\theta) $$
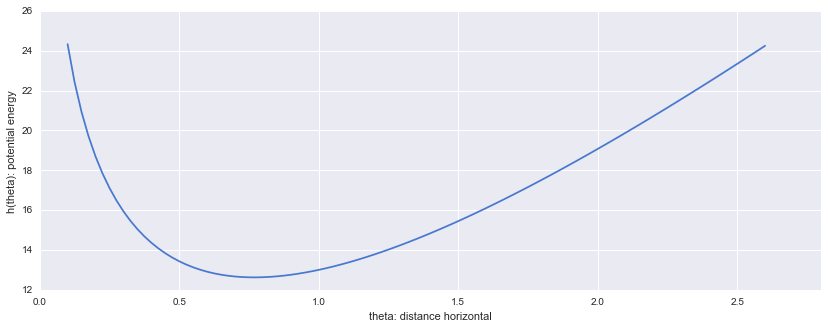
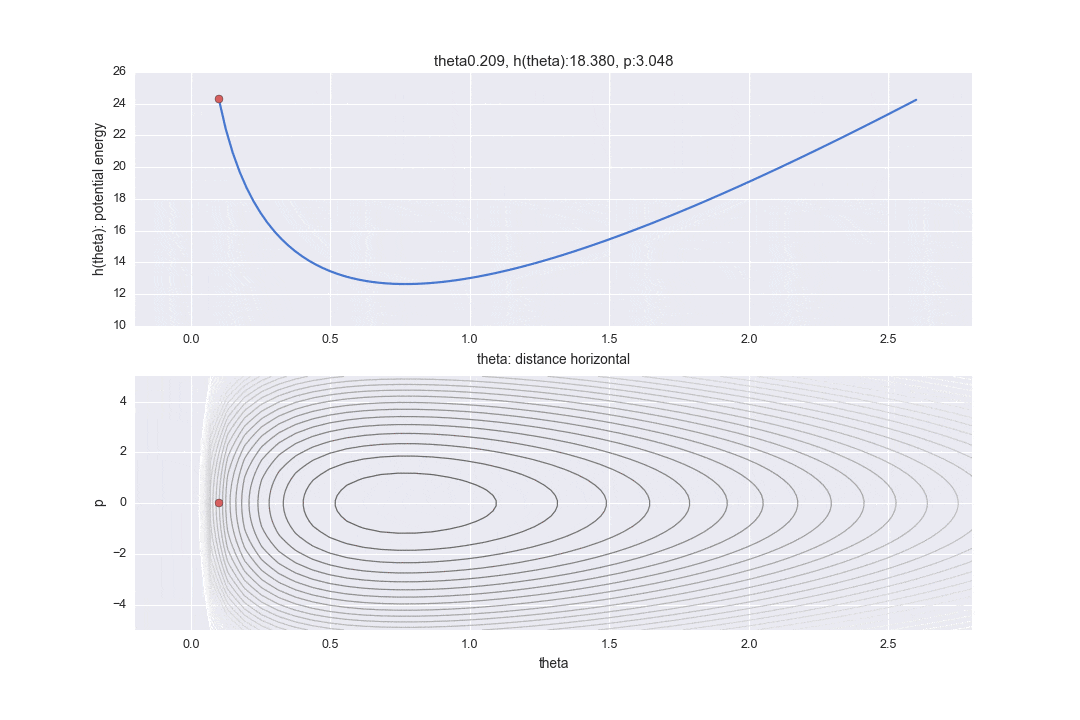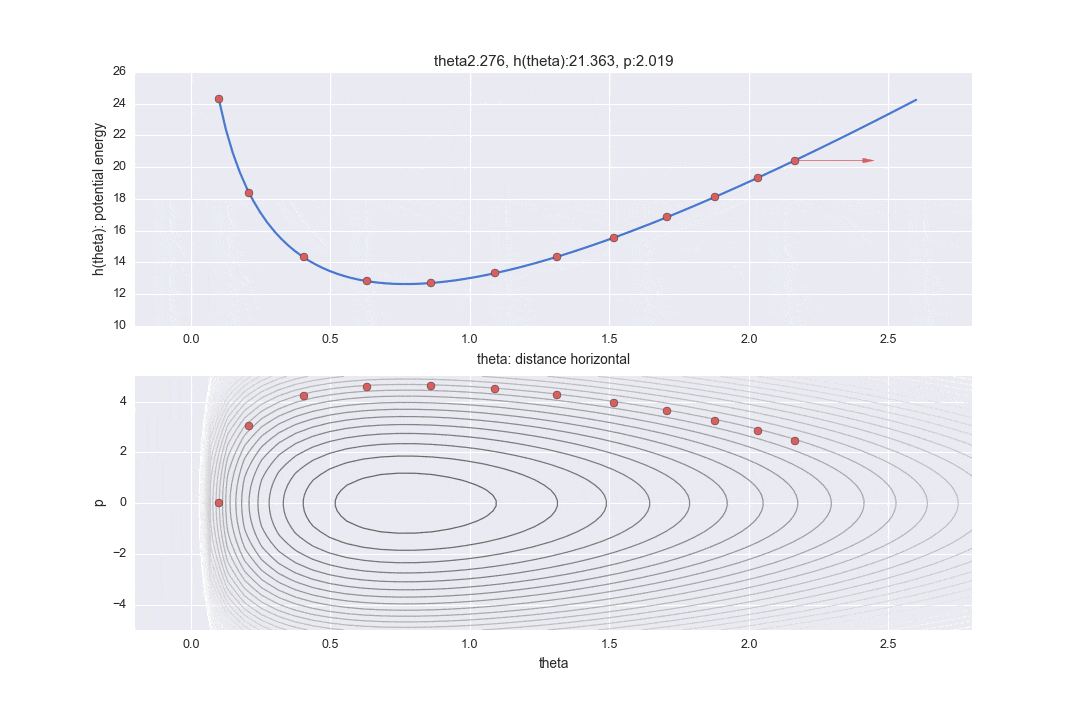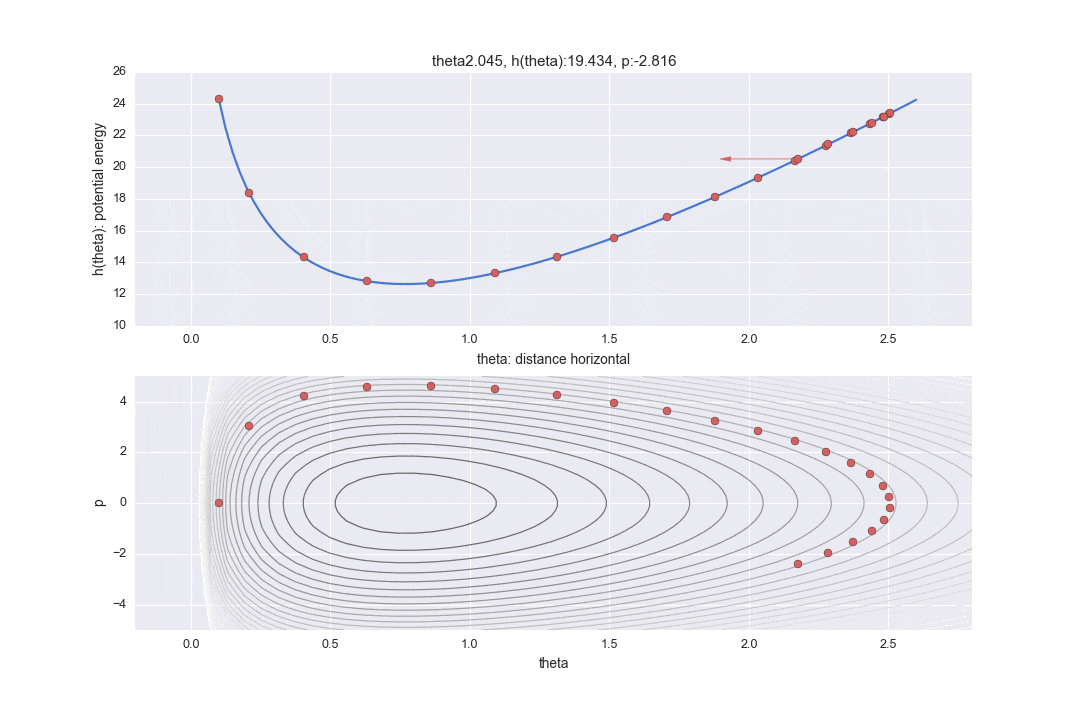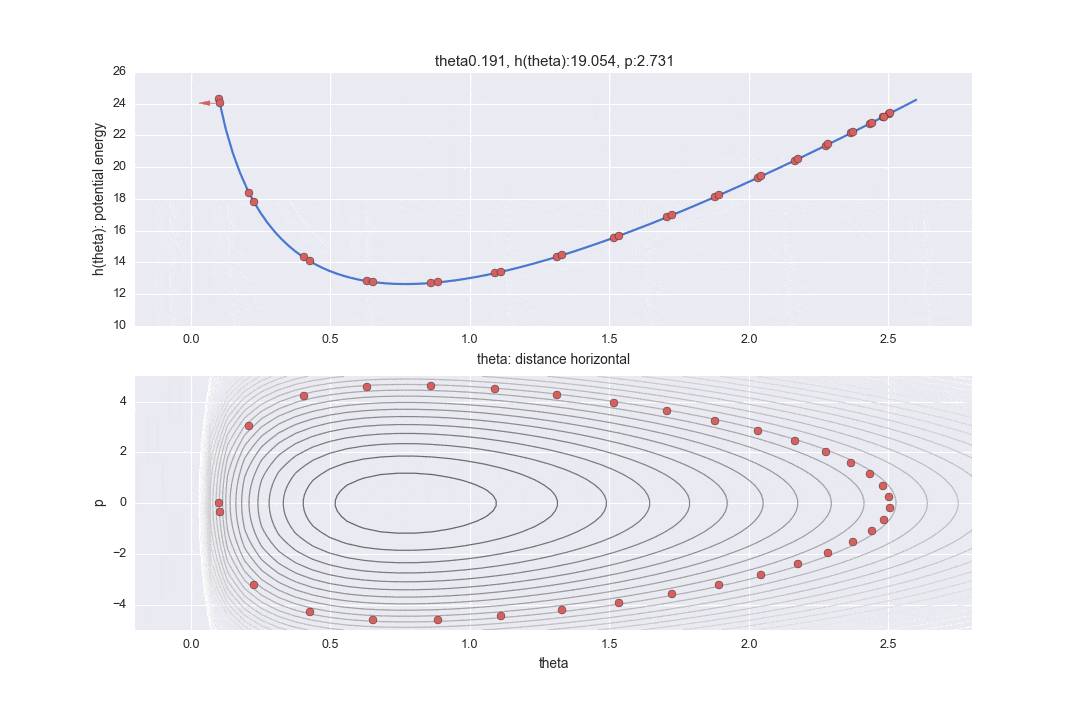
が物理で言う位置エネルギーに相当すると考えます。今回パラメーターには$\alpha=11, \lambda=13$を使います。グラフにすると下記のようなものになります。
位置エネルギー$h(\theta)$と運動エネルギー$p$の関係性から導かれれるハミルトニアン
$$H(\theta, p) = h(\theta) + {1 \over 2} p^2$$
が外部からの力が加わらなければ一定となると言う性質を考えると、位置エネルギーが下がれば運動エネルギーが上昇する関係にあります。この様子をアニメーションにしたものが下記の上の図になります。赤い矢印の長さで運動エネルギー$p$の大きさを表しています。
また、下の部分のグラフは横軸を水平距離$\theta$、縦軸を運動エネルギー$p$で表したもので、位相空間といわれるもののグラフです。(教科書と違い、上のグラフと横軸を合わせるために縦横逆にした図になっています。)等高線はハミルトニアンが一定になっている部分を表します。なので、ハミルトニアン一定である前提で、対応している水平位置と運動エネルギーが違う見方の2つの表示方法で示されています。
リープフロッグ法
上記の図のように、うまくハミルトニアン一定のところを動くように数値計算する手法としてリープフロッグ法が使われます。理論の詳細は書籍を参考にいただくとして、ここではpythonのコードを掲載します。$p$の次の位置を半分ずつ計算することで数値計算による誤差を少なくする手法です。
# function definitions
def h(theta):
global lam, alpha
return lam * theta - (alpha-1)*np.log(theta)
def dh_dtheta(theta):
global lam, alpha
return lam - (alpha - 1)/theta
def hamiltonian(p, theta):
return h(theta) + 0.5*p**2
vhamiltonian = np.vectorize(hamiltonian) # vectorize
def leapfrog_nexthalf_p(p, theta, eps=0.01):
"""
1/2ステップ後のpを計算
"""
return p - 0.5 * eps* dh_dtheta(theta)
def leapfrog_next_theta(p, theta, eps=0.01):
"""
1ステップ後のθを計算
"""
return theta + eps*p
def move_one_step(theta, p, eps=0.01, L=100, stlide=1):
"""
リープフロッグ法でL回移動した1ステップを実行
"""
ret = []
ret.append([1, p, theta, hamiltonian(p,theta)])
for _ in range(L):
p = leapfrog_nexthalf_p(p, theta, eps)
theta = leapfrog_next_theta(p, theta, eps)
p = leapfrog_nexthalf_p(p, theta, eps)
ret.append([1, p, theta, hamiltonian(p,theta)])
return ret[::stlide]
# リープフロッグ法の実行
# initial param
theta = 0.1
p = 0
eps = 0.05
L = 96
result = move_one_step(theta, p, eps=eps, L=100, stlide=1)
リープフロッグ法による遷移と、標準正規分布による運動量pの変更
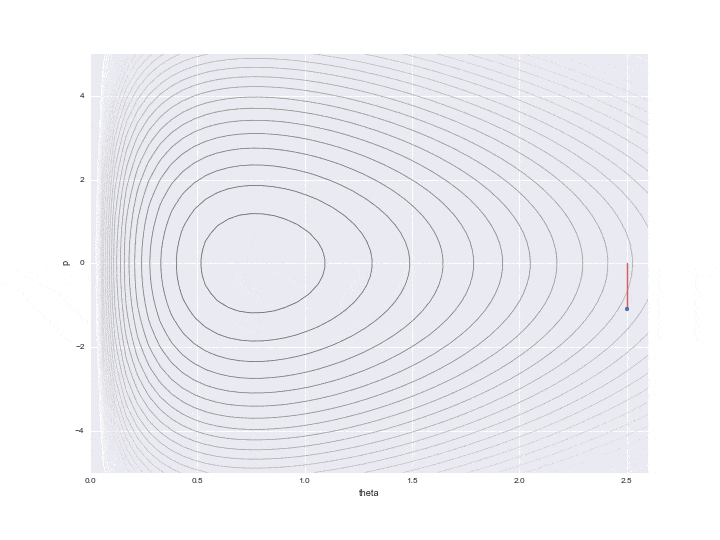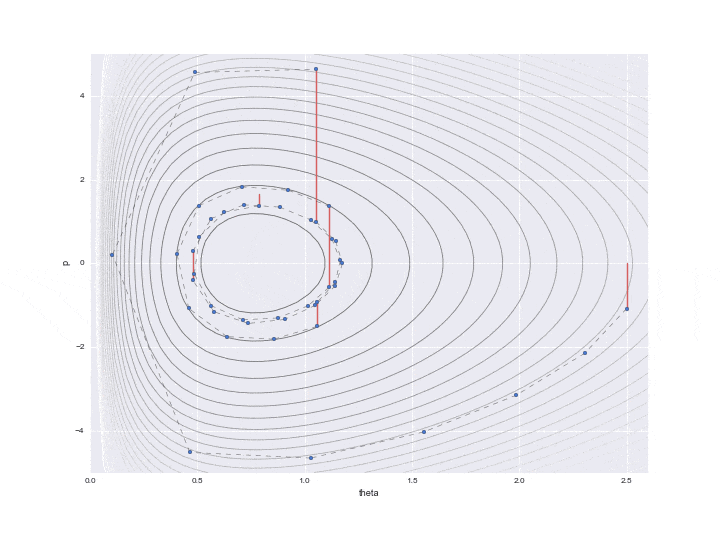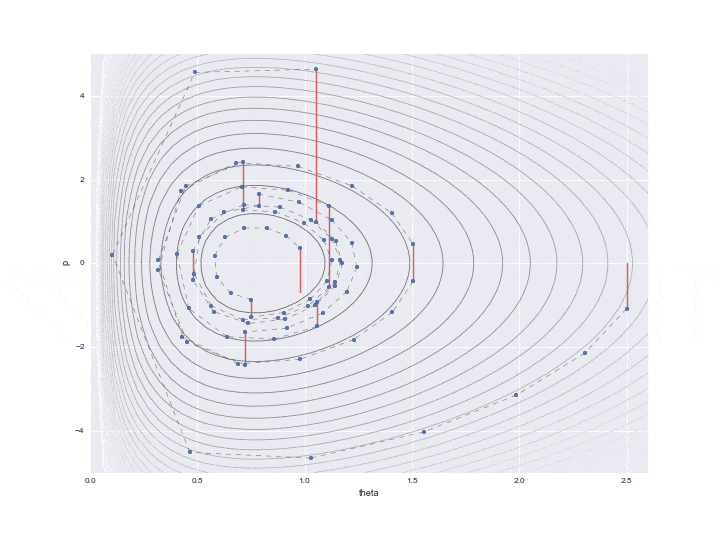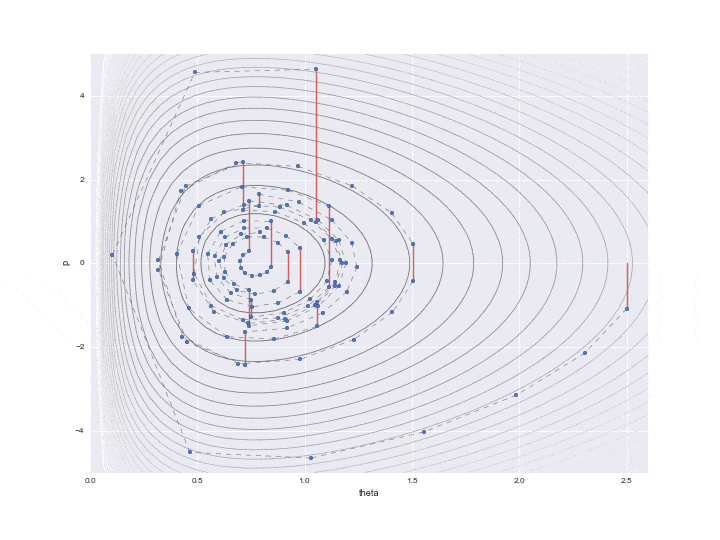
この$L$で指定した1回の遷移を下記のグラフの点線で表しています。L個の軌跡をすべて書くと大変だったので、12個飛ばしで記載しています。なので本当はもっと細かく点が移動しています。
また、途中途中で赤い線が表示されていますが、これはL回遷移したのち、一度位置エネルギーをランダムに変更したことを表しています。具体的には
p = rd.normal(loc=0,scale=scale_p) # ------(*)
というコードで表されるように標準正規分布に従う乱数で$p$を更新しています。(ここでなぜ**「標準」**正規分布を使うのか、理解できていません。分散をパラメーターとして調節できても悪くないような・・・。ご存知の方がいたら教えてください・・・。)ここでハミルトニアンの保存が崩れ、異なるハミルトニアンの値の等高線をまたL回分移動することになるのです。実際にサンプリングに使うのはこの赤い線が描かれる直前の点1つになり、残りの値は単なる計算途中の経過の値として捨ててしまいます。
rd.seed(123)
theta = 2.5
eps = 0.01
T = 15
step = []
prev_p = 0
for tau in range(T):
p = rd.normal(loc=0,scale=scale_p) # ------(*)
step.append([2, p, prev_p, 0])
one_step = move_one_step(theta, p, eps=eps, L=96, stlide=12)
theta = one_step[-1][2]
step.extend(one_step)
prev_p = one_step[-1][1]
print len(step)
def animate(nframe):
global num_frame, n
sys.stdout.write("{}, ".format(nframe))
if step[n][0] == 1:
plt.scatter(step[n][2], step[n][1], s=20, zorder=100)
if step[n-1][0] == 1:
plt.plot([step[n-1][2], step[n][2]],[step[n-1][1], step[n][1]], c="k", ls="--", lw=.8, alpha=0.5)
else:
theta = step[n+1][2]
plt.plot([theta, theta], [step[n][2], step[n][1]], c="r")
n += 1
num_frame = len(step)-1
n = 0
scale_p = 1
fig = plt.figure(figsize=(12,9))
xx = np.linspace(0.01, 2.6)
yy = np.linspace(-5,5)
X, Y = np.meshgrid(xx, yy)
Z = vhamiltonian(Y, X)
plt.contour(X, Y, Z, linewidths=1, cm=cm.rainbow, levels=np.linspace(0,40,40))
plt.ylabel("p")
plt.xlabel("theta")
plt.xlim(0,2.6)
plt.ylim(-5,5)
anim = ani.FuncAnimation(fig, animate, frames=int(num_frame), blit=True)
anim.save('hmc_sampling_detail.gif', writer='imagemagick', fps=5, dpi=60)
サンプリング
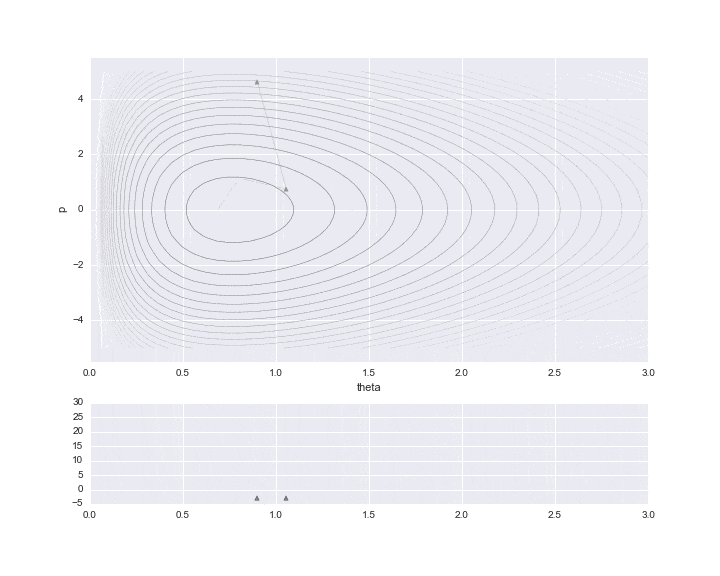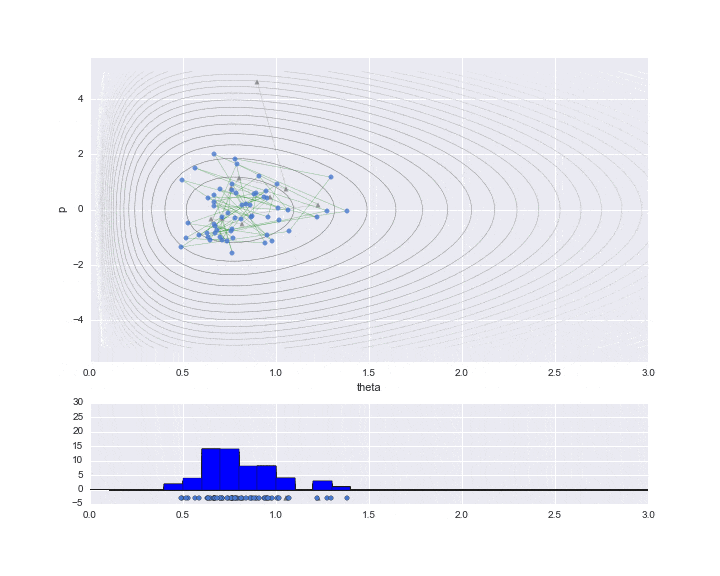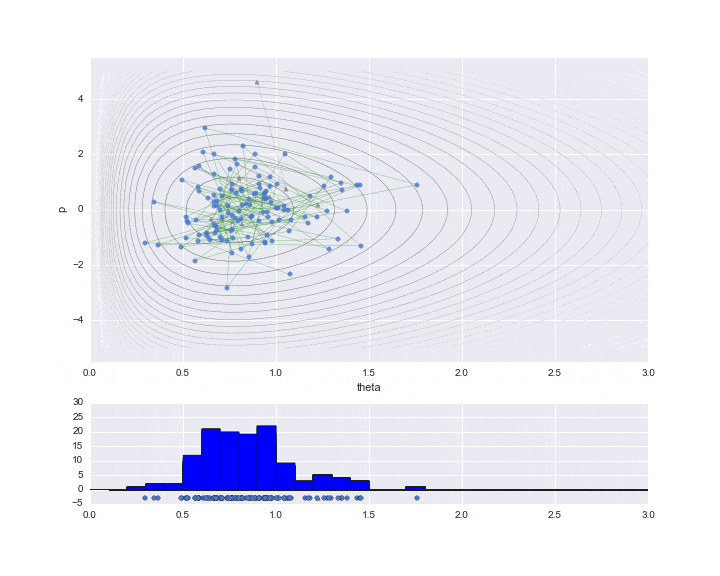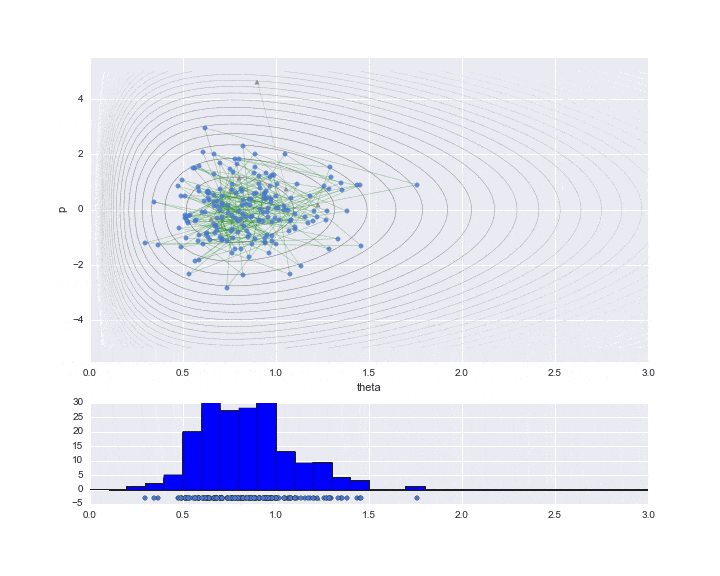
実際に必要なデータだけをプロットした結果が下記です。
また、
$$ r= \exp \left( H(\theta^{(t)}, p^{(t)}) - H(\theta^{(a)}, p^{(a)})\right) $$
という値を$\min(1, r)$として受容率とするため、
r = np.exp(prev_hamiltonian-H) # -----(**)
とrd.uniform()を比較して受容、非受容を決定しています。ですが、この例の場合、一度も棄却されなかったのですべて受容されています。
burn-in期間を10と設定しており、その間はサンプリングされた値を▲で示しています。
下段のグラフが推定対象となる$\theta$の値のヒストグラムです。まだ200弱しかサンプリングしていませんが、右に歪んだガンマ分布のような分布形状のヒストグラムになっていることが見て取れます。
# HMC simulation
rd.seed(71)
scale_p = 1
# initial param
theta = 2.5
p = rd.normal(loc=0,scale=scale_p)
eps = 0.01
L = 100
T = 10000
sim_result = []
prev_hamiltonian = hamiltonian(p,theta)
sim_result.append([ p, theta, prev_hamiltonian, True])
for t in range(T):
prev_p = p
prev_theta = theta
prev_hamiltonian = hamiltonian(p,theta)
for i in range(L):
p = leapfrog_nexthalf_p(p, theta, eps=eps)
theta = leapfrog_next_theta(p, theta, eps=eps)
p = leapfrog_nexthalf_p(p, theta, eps=eps)
H = hamiltonian(p,theta)
r = np.exp(prev_hamiltonian-H) # -----(**)
if r > 1:
sim_result.append([ p, theta, hamiltonian(p,theta), True])
elif r > 0 and rd.uniform() < r:
sim_result.append([ p, theta, hamiltonian(p,theta), True])
else:
sim_result.append([ p, theta, hamiltonian(p,theta), False])
theta = prev_theta
p = rd.normal(loc=0,scale=scale_p)
sim_result = np.array(sim_result)
df = pd.DataFrame(sim_result, columns="p,theta,hamiltonian,accept".split(","))
# df
print "accept ratio: ", np.sum([df.accept == 1])/len(df)
受容率はほぼ100%に近くなりました ![]()
accept ratio: 0.999900009999
この様子をT=200までのアニメーションを生成したコードがこちらです。
def animate(nframe):
global num_frame, n
sys.stdout.write("{}, ".format(nframe))
#### 上段 #####
if n < burn_in:
marker = "^"
color = "gray"
lc = "gray"
else:
marker = "o"
color = "b"
lc = "green"
if sim_result[i,3] == 0:
marker = "x"
color = "r"
lc = "gray"
axs[0].scatter(sim_result[n,1], sim_result[n,0], s=20, marker=marker,
zorder=100, alpha=0.8, color=color) #,
if n > 1:
axs[0].plot([sim_result[n-1,1], sim_result[n,1]],
[sim_result[n-1,0], sim_result[n,0]], c=lc, lw=0.5, alpha=0.4)
#### 下段 #####
axs[1].scatter(sim_result[n,1], -3, alpha=1, marker=marker, c=color)
if n > burn_in:
hist_data = pd.DataFrame(sim_result[burn_in:n], columns="p,theta,hamiltonian,accept".split(","))
hist_data = hist_data[hist_data.accept ==1]
hist_data.theta.hist(bins=np.linspace(0,3,31),ax=axs[1], color="blue",)
### ========================
n += 1
burn_in = 10
num_frame = 200
n = 1
n_col = 1
n_row = 2
fig, _ = plt.subplots(n_row, n_col, sharex=False, figsize=(10,8))
gs = gridspec.GridSpec(n_row, n_col, height_ratios=[3,1])
axs = [plt.subplot(gs[i]) for i in range(n_row*n_col)]
xx = np.linspace(0.01, 3)
yy = np.linspace(-5,5)
X, Y = np.meshgrid(xx, yy)
Z = vhamiltonian(Y, X)
axs[0].contour(X, Y, Z, linewidths=0.5, cm=cm.rainbow, levels=np.linspace(0,40,40))
axs[0].set_ylabel("p")
axs[0].set_xlabel("theta")
axs[0].set_xlim(0,3)
axs[1].set_xlim(0,3)
axs[1].set_ylim(-5,30)
anim = ani.FuncAnimation(fig, animate, frames=int(num_frame), blit=True)
anim.save('hmc_simulation2.gif', writer='imagemagick', fps=4, dpi=72)
本格的なサンプリング
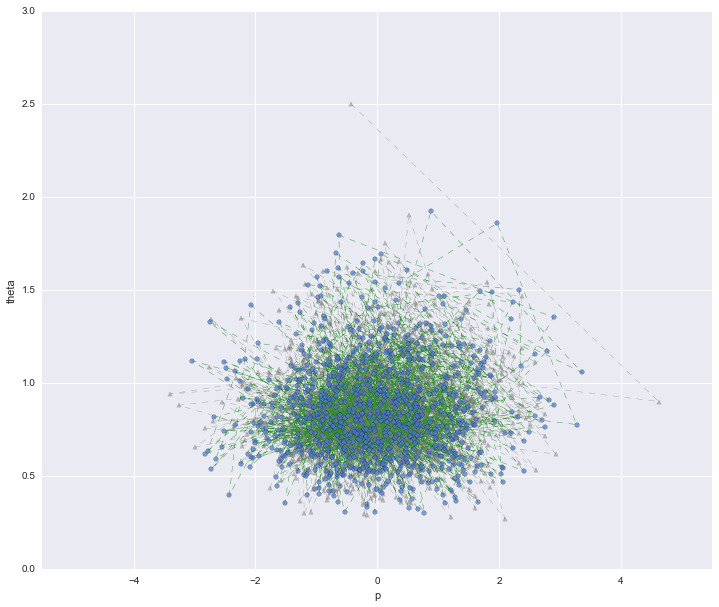
上記まではアニメーションのためにTを200と少なめにしていましたが、T=10000すべてをプロットした図がこちらです。burn-inは1000に指定しています。
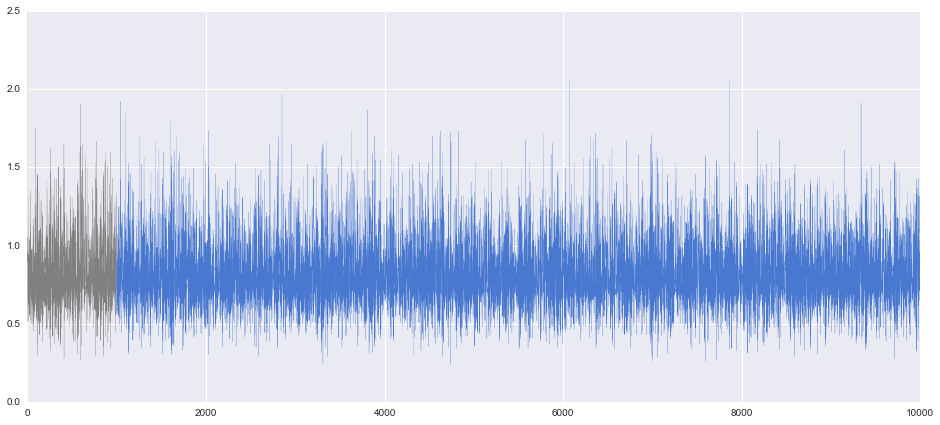
$\theta$のトレースプロットです。前半のグレーの部分がburn-in部分です。
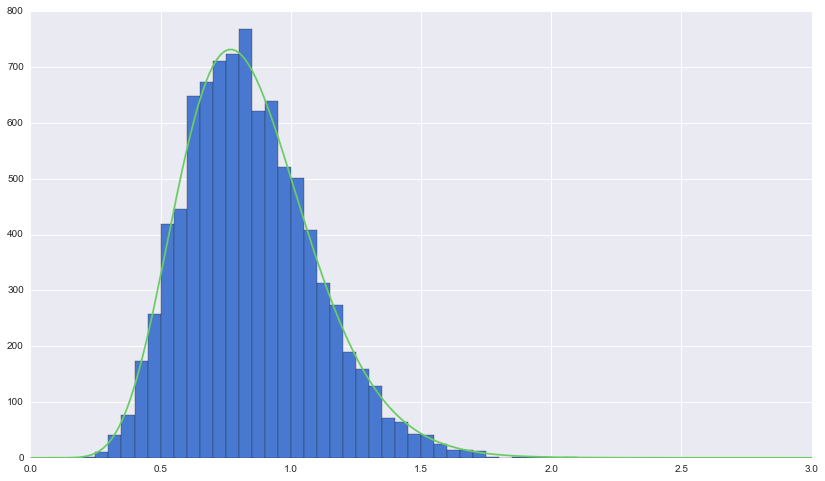
結果をヒストグラムにしてみたものがこちらです。$\alpha=11, \lambda=13$のガンマ分布と比較してみると、ほぼ一致していることが見て取れます ![]()
おわりに
ハミルトニアンモンテカルロ法を使うことで、サンプリングの受容率が上がるということでしたが、確かに高い受容率(今回はほぼ100%)となっていることがわかりました ![]()
参考
「基礎からのベイズ統計学 -ハミルトニアンモンテカルロ法による実践的入門-」 (豊田秀樹 編著)
https://www.asakura.co.jp/books/isbn/978-4-254-12212-1/
本記事のコード全文
https://github.com/matsuken92/Qiita_Contents/blob/master/Bayes_chap_05/HMC_Gamma-for_Publish.ipynb
(PCでの閲覧推奨、スマホではデスクトップモードで閲覧してください。)
MacでPythonからアニメーションGIFを生成する環境設定
http://qiita.com/kenmatsu4/items/573ca0733b192d919d0e
基礎からのベイズ統計学入門 輪読会
http://stats-study.connpass.com/event/27129/
→ 僭越ながら、私が主催しているこの本の勉強会です。
-
ガンマ分布はそのままでも十分情報が取れる比較的簡単な分布ですが、ここではこれが難しい事後分布であったと仮定して進めます。この事後分布からHMCを用いて乱数を発生させて、得られた乱数列から事後分布の情報を探り出そうということになります。 ↩