Go to Qiita Advent Calendar 2024 Top
LoginSignup
3
6

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@matsukura04583(善浩 松倉)

<科目> 深層学習: Day2 CNN

Last updated at Posted at 2020-01-07

#<科目> 深層学習　

目次
[深層学習: Day1 NN ]
(https://qiita.com/matsukura04583/items/6317c57bc21de646da8e)
[深層学習: Day2 CNN ]
(https://qiita.com/matsukura04583/items/29f0dcc3ddeca4bf69a2)
[深層学習: Day3 RNN]
(https://qiita.com/matsukura04583/items/9b77a238da4441e0f973)
[深層学習: Day4 強化学習・Tensor Flow]
(https://qiita.com/matsukura04583/items/50806b750c8d77f2305d)

##深層学習: Day2 CNN (講義の要約)

深層学習全体像の復習–学習概念

  1. 入力層に値を入力
  2. 重み、バイアス、活性化関数で計算しながら値が伝わる
  3. 出力層から値が伝わる
  4. 出力層から出た値と正解値から、誤差関数を使って誤差を求める
  5. 誤差を小さくするために重みやバイアスを更新する.(特に重要である)
  6. 1〜5の操作を繰り返すことにより、出力値を正解値に近づけていく
<img width="397" alt="スクリーンショット 2020-01-02 10.07.45.png" src="https://qiita-image-store.s3.ap-northeast-1.amazonaws.com/0/357717/f060b503-960a-b313-dd41-71c4c255f6fb.png">

誤差逆伝播のイメージ図
スクリーンショット 2020-01-02 10.12.55.png
スクリーンショット 2020-01-02 10.36.12.png
スクリーンショット 2020-01-02 10.38.48.png
スクリーンショット 2020-01-02 10.39.04.png

メリットとして、誤差の計算結果から微分を逆算することで、不要な再帰的計算を避けて微分を算出できる。計算コストの削減。

深層モデルのための学習テクニック

  • Section1) 勾配消失問題について全体像

    （前回の流れと課題全体像のビジョン）
    　　　勾配消失問題
    　　　誤差逆伝播法が下位層に進んでいくに連れて、勾配がどんどん緩やかになっていく。そのため、勾配降下法による、更新では下位層のパラメータはほとんど変わらず、訓練は最適値に収束しなくなる。シグモイド関数→（問題）大きな値では出力の変化が微小なため、勾配消失問題を引き起こす事があった。

    • 1-1活性化関数

      ReLU関数

      　　　　勾配消失問題の回避とスパース化に貢献することで良い成果をもたらしている。

      　　　　※勾配消失問題・スパース化については確率的勾配降下法の解説後に詳しく触れる予定

    • 1-2初期値の設定方法

      重みの初期値設定-Xavier

      Xavierの初期値を設定する際の活性化関数
      ReLU関数
      シグモイド（ロジスティック）関数
      双曲線正接関数

スクリーンショット 2020-01-02 11.01.51.png 
           **重みの初期値設定-He**

Heの初期値を設定する際の活性化関数
Relu関数
スクリーンショット 2020-01-02 11.04.56.png
初期値の設定方法
重みの要素を、前の層のノード数の平方根で除算した値に対し、ルート２を掛け合わせた値。

 + 1-3バッチ正規化

        バッチ正規化とは$\Rightarrow$ミニバッチ単位で、入力値のデータの偏りを抑制する手法

バッチ正規化の使い所とは︖$\Rightarrow$活性化関数に値を渡す前後に、バッチ正規化の処理を孕んだ層を加える

u^{(l)}=w^{(l)}z^{(l)}+b^{(l)}  または　z
スクリーンショット 2020-01-02 11.52.05.png スクリーンショット 2020-01-02 11.52.18.png スクリーンショット 2020-01-02 11.52.54.png
  • Section2)学習率最適化手法について全体像

    （前回の流れと課題全体像のビジョン）

　　　　+ 勾配降下法の復習
スクリーンショット 2020-01-02 12.01.44.png

  • 学習率の復習学
    習率の値が大きい場合・最適値にいつまでもたどり着かず発散してしまう。学習率の値が小さい場合・発散することはないが、小さすぎると収束するまでに時間がかかってしまう。
    ・大域局所最適値に収束しづらくなる。

    • Section2)続き(図が入るとインデントが崩れてしまう？)

      • 2-1モメンタム

      • スクリーンショット 2020-01-02 12.14.11.png
      • スクリーンショット 2020-01-02 12.15.29.png

      • 2-2AdaGrad

      • スクリーンショット 2020-01-02 12.16.20.png
スクリーンショット 2020-01-02 12.16.36.png 
 + 2-3 RMSProp
 + <img width="665" alt="スクリーンショット 2020-01-02 12.17.21.png" src="https://qiita-image-store.s3.ap-northeast-1.amazonaws.com/0/357717/0ab21139-f6ed-7bcf-27f6-b7ae5d9631c5.png">
スクリーンショット 2020-01-02 12.17.42.png 
 + 2-4Adam
  + Adamとは︖$\Rightarrow$モメンタムの、過去の勾配の指数関数的減衰平均・RMSPropの、過去の勾配の2乗の指数関数的減衰平均上記をそれぞれ孕んだ最適化アルゴリズムである。
  + Adamのメリットとは︖$\Rightarrow$モメンタムおよびRMSPropのメリットを孕んだアルゴリズムである。

  • Section3)過学習について全体像
    （前回の流れと課題全体像のビジョン）
    テスト誤差と訓練誤差とで学習曲線が乖離すること。︖$\Rightarrow$特定の訓練サンプルに対して、特化して学習する。
    原因は、パラメータの数が多い、パラメータの値が適切でない、ノードが多いetc...
    $\Rightarrow$ネットワークの自由度(層数、ノード数、パラメータの値etc...)が高い

    • 3-1 L1正則化、L2正則化

      正則化とは︖︖$\Rightarrow$ネットワークの自由度(層数、ノード数、パラメータ値etc...)を制約すること。
      ︖$\Rightarrow$正則化手法を利用して過学習を抑制する

      • Weight decay(荷重減衰)
        • 過学習の原因
        • 重みが大きい値をとることで、過学習が発生することがある。
        • 重みが大きい値は、学習において重要な値であり、重みが大きいと過学習が起こる。
        • 過学習の解決策
        • 誤差に対して、正則化項を加算することで、重みを抑制する学習させていくと、重みにばらつきが発生する。
        • 過学習がおこりそうな重みの大きさ以下で重みをコントロールし、かつ重みの大きさにばらつきを出す必要がある。

    • 3-2ドロップアウト

    • 過学習の課題・ノードの数が多いドロップアウトとは︖$\Rightarrow$ランダムにノードを削除して学習させること。メリットとして、データ量を変化させずに、異なるモデルを学習させていると解釈できる。

    • スクリーンショット 2020-01-02 13.59.09.png

###畳み込みニューラルネットワークについて

  • 畳み込みニューラルネットワークについて
    • Section4)畳み込みニューラルネットワークの概念

      CNNの構造図

      スクリーンショット 2020-01-02 14.09.10.png

      LeNetの構造図
スクリーンショット 2020-01-02 14.11.19.png 
 + 4-1畳み込み層
    + 4-1-1バイアス
    + 畳み込み層演算概念(バイアス)
    + <img width="729" alt="スクリーンショット 2020-01-02 14.16.56.png" src="https://qiita-image-store.s3.ap-northeast-1.amazonaws.com/0/357717/34ae6181-ed41-f49a-4718-60616cf503c9.png">

    + 4-1-2パディング
    + 畳み込み層演算概念(パディング)
    + <img width="691" alt="スクリーンショット 2020-01-02 14.18.01.png" src="https://qiita-image-store.s3.ap-northeast-1.amazonaws.com/0/357717/1164306c-03bc-3d2b-98a3-73a357f0e2e7.png">

    + 4-1-3ストライド
    + 畳み込み層演算概念(パディング)
    + <img width="600" alt="スクリーンショット 2020-01-02 14.20.18.png" src="https://qiita-image-store.s3.ap-northeast-1.amazonaws.com/0/357717/f611fe81-e3ad-e051-aa7c-21ef7c49639c.png">

    + 4-1-4チャンネル
    + 畳み込み層演算概念(チャンネル)
    + <img width="565" alt="スクリーンショット 2020-01-02 14.21.03.png" src="https://qiita-image-store.s3.ap-northeast-1.amazonaws.com/0/357717/fb680b77-8cb3-d945-b2ca-c8f05bcb4143.png">
    + 全結合で画像を学習した際の課題　全結合層のデメリット$\Rightarrow$画像の場合、縦、横、チャンネルの3次元データだが、1次元のデータとして処理される。$\Rightarrow$RGBの各チャンネル間の関連性が、学習に反映されないということ。

    + 4-2プーリング層
    + プーリング層の概念図
    + <img width="712" alt="スクリーンショット 2020-01-02 14.25.11.png" src="https://qiita-image-store.s3.ap-northeast-1.amazonaws.com/0/357717/90ecc24a-8ceb-1ec9-542f-19e1ea9b6141.png">

+ Section5)最新のCNN
    + 5-1 AlexNet
    + AlexNetのモデル説明
    + モデルの構造
        + 5層の畳み込み層およびプーリング層など、それに続く3層の全結合層から構成される。
        
    + 過学習を防ぐ施策
        + サイズ4096の全結合層の出力にドロップアウトを使用している。
        + <img width="519" alt="スクリーンショット 2020-01-02 14.50.59.png" src="https://qiita-image-store.s3.ap-northeast-1.amazonaws.com/0/357717/dc18e002-9a0a-4e72-79d0-7cc2f1d7a958.png">

#演習

DN06_Jupyter演習

##確認テストの考察

【P12】連鎖律の原理を使い、dz/dxを求めよ。

     z = t^2,t=x+y

⇒【考察】
次のような計算にて求める事ができる。

 \frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}

,t=x+y

z = t^2なのでtで微分すると \frac{dz}{dt}=2t


t=x+yなのでxで微分すると \frac{dt}{dx}=1


\frac{dz}{dx}=2t・1=2t=2(x+y)

【P20】シグモイド関数を微分した時、入力値が0の時に最大値をとる。その値として正しいものを選択肢から選べ。（1）0.15（2）0.25（3）0.35（4）0.45

⇒【考察】
sigumoidの微分

     (sigmoid)'=(1-sigmoid)(sigmoid)

sigmoid関数は0.5で最大となるので、

     (sigmoid)'=(1-0.5)(0.5)=0.25  となる

【P28】重みの初期値に0を設定すると、どのような問題が発生するか。簡潔に説明せよ。
⇒【考察】
勾配が得られない場合がある。前述で重みの初期値の公式が挙げられたので活用してゆく。

【P31】一般的に考えられるバッチ正規化の効果を2点挙げよ。
⇒【考察】
　　中間層のパラメータの分布が適切になる。
　　中間層の学習が安定化する
この手法は2015年に提案された新しい手法であるにもかかわらず現在広く使われてる。．

【P36】例題チャレンジ
スクリーンショット 2020-01-02 11.54.43.png

正解：data_x[i:i_end], data_t[i:i_end
•【解説】バッチサイズだけデータを取り出す処理である。
⇒【考察】記載が似通って、間違いやすいので気をつけよう。

【P63】確認テスト

スクリーンショット 2020-01-02 12.38.45.png

⇒【考察】
答えは「a」
スクリーンショット 2020-01-02 12.50.27.png
図と一緒に覚えると良い。

【P68】L1正則化を表しているグラフはどちらか答えよ。
⇒【考察】
答えは右
スクリーンショット 2020-01-02 12.37.49.png

図と一緒に覚えると良い。Lassoは菱形が特徴的な図である。（Ridgeは円形）

【P69】例題チャレンジ

スクリーンショット 2020-01-02 13.31.21.png

⇒【考察】
答えは(4)param
スクリーンショット 2020-01-02 13.40.33.png
計算式と一緒に憶えると良い。L1 ,L2を正しく理解する。

【P71】例題チャレンジ

スクリーンショット 2020-01-02 13.44.02.png

⇒【考察】
答えは『sign(param)』
【解説】L1ノルムは、|param|なのでその勾配が誤差の勾配に加えられる。つまり、sign(param)である。signは符号関数である。
初めて出る、sign符号関数についても理解が必要。

【P78】例題チャレンジ
スクリーンショット 2020-01-02 13.53.49.png
⇒【考察】
　正解：image[top:bottom, left:right, :]
【解説】imageの形式が(縦幅, 横幅, チャンネル)であるのも考慮する。

【P100】確認テスト
サイズ6×6の入力画像を、サイズ2×2のフィルタで畳み込んだ時の出力画像のサイズを答えよ。なおストライドとパディングは1とする。
⇒【考察】
答え　７✖️７
入力サイズ高さ(H),入力サイズ幅(W)
Output Hight（OH）
Output Width（OW）
Filler Hight（FH）
Filler Width（FW）
ストライド(S)
パンディング(P)

   OH =\frac{H+2P-FH}{S}+1 =\frac{6+2・1-２}{1}+1=7

   OW =\frac{W+2P-FW}{S}+1 =\frac{6+2・1-２}{1}+1=7

決まった計算方法なので、公式として覚えておくと便利。

#演習
##DN23_Jupyter演習

スクリーンショット 2020-01-02 15.46.59.png

ReLU-Xavierの組み合わせに変更した結果
スクリーンショット 2020-01-02 15.36.15.png
Sigmoid-HEの組み合わせに変更した結果
スクリーンショット 2020-01-02 15.43.35.png

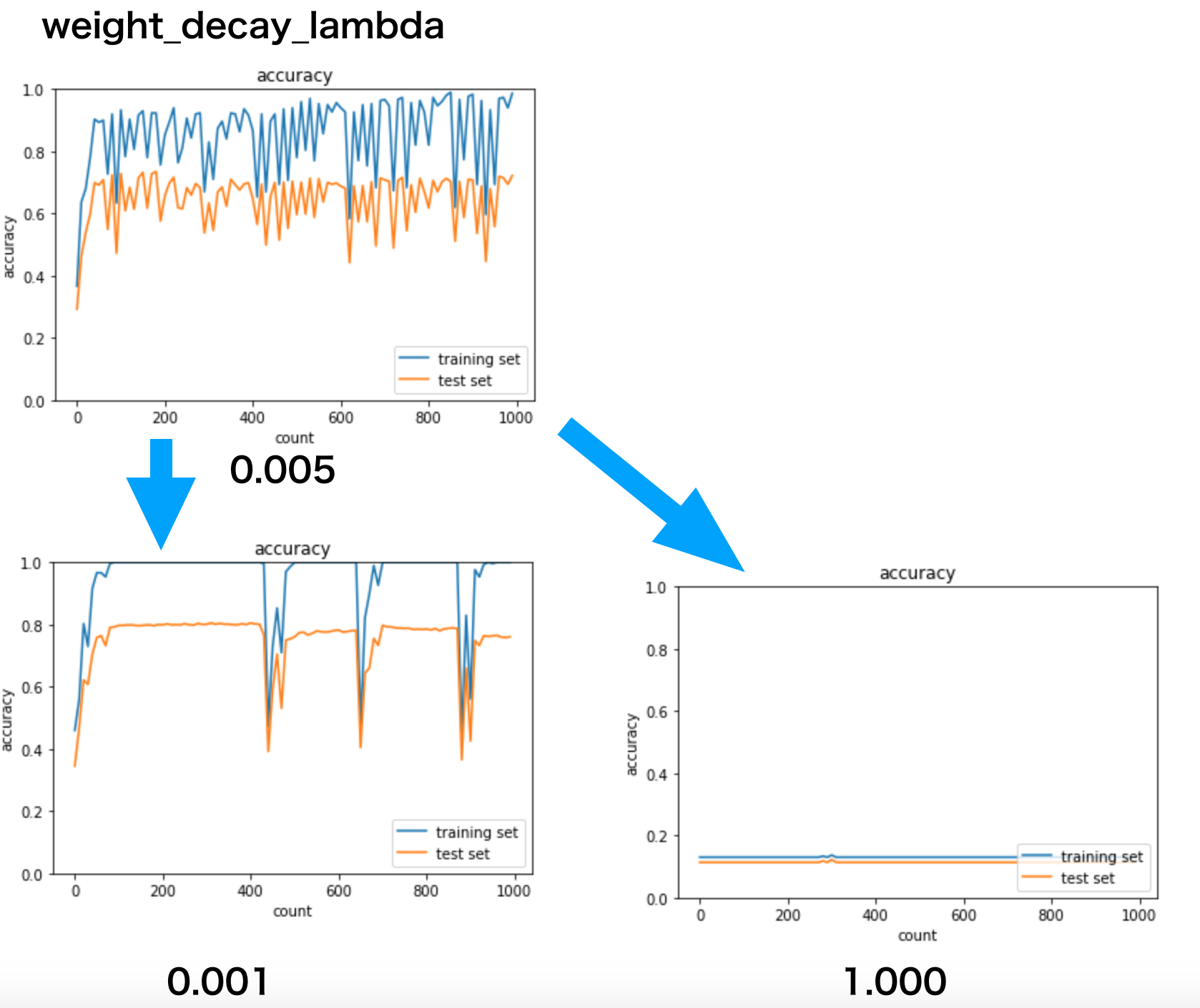
##DN32_Jupyter演習(Dropout)
スクリーンショット 2020-01-03 2.28.29.png
スクリーンショット 2020-01-03 2.31.55.png

##DN35_Jupyter演習(im2col)
[try] im2colの処理を確認しよう
・関数内でtransposeの処理をしている行をコメントアウトして下のコードを実行してみよう
・input_dataの各次元のサイズやフィルターサイズ・ストライド・パディングを変えてみよう

⇒【考察】
演習結果は次のとうり。

python
# im2colの処理確認
input_data = np.random.rand(2, 1, 4, 4)*100//1 # number, channel, height, widthを表す
print('========== input_data ===========\n', input_data)
print('==============================')
filter_h = 3
filter_w = 3
stride = 1
pad = 0
col = im2col(input_data, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad)
print('============= col ==============\n', col)
print('==============================')
スクリーンショット 2020-01-03 3.05.36.png

以下のようにinput_dataの各次元のサイズやフィルターサイズ・ストライド・パディングを変えてみる。

python
filter_h = 6
filter_w = 6
stride = 2
pad = 1
スクリーンショット 2020-01-03 3.11.05.png

・im2colとcol2imでは全く同じように戻る訳ではないことを理解した上で利用する必要がある。
・そもそも使うシーンが違う。im2colは畳み込み時に利用するが、col2imは最終的な出力に利用される。

[try] col2imの処理を確認しよう
・im2colの確認で出力したcolをimageに変換して確認しよう
⇒【考察】

python
# col2imの処理を追加
img = col2im(col, input_shape=input_data.shape, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad)
print(img)
スクリーンショット 2020-01-03 3.23.19.png ##DN37_Jupyter演習(3) スクリーンショット 2020-01-03 3.30.52.png

・畳み込み処理は学習するのに時間がかかるので注意が必要。ストレスなく処理するには、PCスペックを上げたり、GPU搭載した機器を用意するのをお勧めします。

3
6
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
6

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?