さてさて ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装 を絶賛学習中です。。
書籍を真ん中くらいまで読み進めて、キホンに立ち返って知識を整理している最中なのですが、その際の覚え書きです。
書籍前半の、パーセプトロンによるXORゲートの作成からはじめて、ニューラルネットワークの定義までを復習してみます。
前提や対象のかた
- ニューラルネットワークって何?というかた。
- 書籍の2章パーセプトロンから、3章ニューラルネットワーク の復習という位置づけですが、書籍の知識は前提としていません。
- 書籍が「ゼロから作る〜」なので、内容は初歩的ですが多少数学的です(平面・空間図形、行列の一次変換(線形代数)を使います) 。
TL;DR
- AND/NAND/ORは単純パーセプトロンで実装出来る
- XOR(排他的論理和)は、OR/NAND をかけてからANDにかけることで実装出来るが、それは隠れ層を持ったニューラルネットワークと同じ意味
- 「行列によるアフィン変換と、活性化関数$h$を合成する」を繰り返す(層を重ねる)ことでニューラルネットワークを構築できる
- 一つの層では不可能であるが、層を重ねることで複雑な出力を行えるようになる。
- ネットワークによる出力値(予測値)を活性化関数で確率に変換することで、多項への「分類」が出来る
- ネットワークによる出力値(予測値)をそのまま用いることで「回帰」をおこなう事が出来る
単純な分類問題
ニューラルネットワークは「この画像データは、0〜9に分類するなら、たぶん'3'です」などと、データを分類するのにつかったりします。
なのでまず、下記のような単純な「分類」問題を考えます。
$x,y$ 平面において、$(x,y)= (0,0),(1,0),(0,1),(1,1)$を
(0,0) → 0\\
(1,0) → 1\\
(0,1) → 1\\
(1,1) → 1
と分類してください。
やってみる
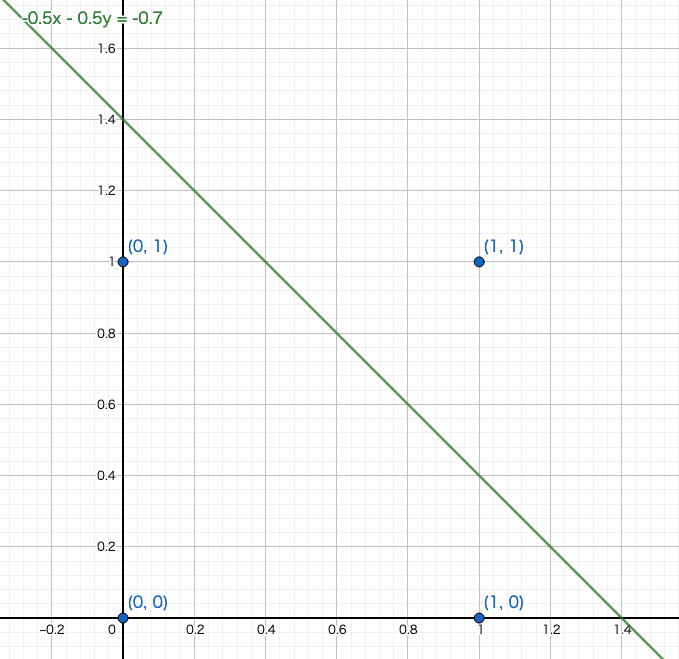
$x,y$平面上で図示してみると、
こんな感じに分割できればよさそうです。
また、$x,y,z$空間上で、三次元で考えてみると、
\begin{align}
z = f(x,y) &=0.5x + 0.5y -0.2 \\
h(z) &=
\left\{
\begin{array}
&1&(if \ z > 0)\\
0 &(if \ z \leq 0)
\end{array}
\right.
\end{align}
という空間上の平面 $f$ を定義し、それが$x,y$平面より上にあれば1,なければ0という定義をすればよさそう。
ようするに $(x,y) → f(x,y) → h(z)$ と合成すれば、先ほどの出力を得られそうです。
図示するとこんな感じ。
ちなみに、この「$z = 0.5x + 0.5y -0.2$」は行列を用いて、
z = (x,y)
\begin{pmatrix}
0.5 \\
0.5
\end{pmatrix}
-0.2
と書けることに注意しておきましょう。
これってORだ
じつは上記の
(0,0) → 0\\
(1,0) → 1\\
(0,1) → 1\\
(1,1) → 1
は、どちらかが1だったら1ということで OR を実装したことになります。
NANDやAND
同様に、NAND(ANDの反対)つまり
(0,0) → 1\\
(1,0) → 1\\
(0,1) → 1\\
(1,1) → 0
を作ってみると、
\begin{align}
z &= -0.5x - 0.5y +0.7 \\
&= (x,y)
\begin{pmatrix}
-0.5 \\
-0.5
\end{pmatrix}
+0.7\\
h(z) &=
\left\{
\begin{array}
&1&(if \ z > 0)\\
0 &(if \ z \leq 0)
\end{array}
\right.
\end{align}
とかで分割すればよさそうです。
平面や空間に図示するとそれぞれこんな感じ。。
$(1,1)$以外の3点の$z$の値が、$x,y$平面より上にある図になってますね。。
ついでにANDをみたす平面は、
\begin{align}
z &= 0.5x + 0.5y -0.7 \\
&= (x,y)
\begin{pmatrix}
0.5 \\
0.5
\end{pmatrix}
-0.7
\end{align}
などでいけそうです。
$(1,1)$だけ、$x,y$平面の上にある図。
行列で一網打尽に表記
さて、これらを行列を用いてもうすこし整理してみると
\begin{align}
(z_1,z_2,z_3) &=( -0.5x - 0.5y +0.7,\ \ \ 0.5x + 0.5y -0.2,\ \ 0.5x + 0.5y -0.7) \\
&= (x,y)
\begin{pmatrix}
-0.5 & 0.5 & 0.5\\
-0.5 & 0.5 & 0.5
\end{pmatrix}
+(0.7,-0.2,-0.7)\\
h(\cdot) &=
\left\{
\begin{array}
&1&(if \ \cdot > 0)\\
0 &(if \ \cdot \leq 0)
\end{array}
\right.
\end{align}
と一網打尽に記載することも可能です。($z_1$はNAND、$z_2$はOR、$z_3$はANDに対応)
パーセプトロンとは
また関数 $h$:
h(\cdot)=
\left\{
\begin{array}
&1&(if \ \cdot > 0)\\
0 &(if \ \cdot \leq 0)
\end{array}
\right.
は階段関数(Step Function)と呼ばれ、下記のような関数となっています。
またここまで見てきたように「複数の値(ここでは$(x,y)$の二値)を受け取って、0か1を出力する機構」をパーセプトロンと呼びます。とくにここまでは、パーセプトロンを一つだけ使った単純パーセプトロンを使用してきました。。
すこし複雑な分類問題
XORはどうする
さて、XOR(排他的論理和)はどうでしょうか。
(0,0) → 0\\
(1,0) → 1\\
(0,1) → 1\\
(1,1) → 0
です。これは下記の図でも分かるとおり、直線では分割することが出来ません。
となっているからですね。つまり単純パーセプトロンではXORを表現出来ないというわけで、このように分割する線を導出するために上記の演算$h(\cdot)とf(\cdot)$を何度か繰り返してみます。1
突然ですが、ココからは $(x,y)$ を$(x_1,x_2)$とかきます。。
まず$(x_1,x_2)$を
\begin{align}
(a_1^{(1)},a_2^{(1)}) &=( -0.5x_1 - 0.5x_2 +0.7,\ \ \ 0.5x_1 + 0.5x_2 -0.2) \\
&= (x_1,x_2)
\begin{pmatrix}
-0.5 & 0.5\\
-0.5 & 0.5
\end{pmatrix}
+(0.7,-0.2)\\
\end{align}
って NANDとORにくぐらせて$a_1^{(1)},a_2^{(1)}$を生成し、さらに既出の
\begin{align}
h(\cdot) &=
\left\{
\begin{array}
&1&(if \ \cdot > 0)\\
0 &(if \ \cdot \leq 0)
\end{array}
\right.
\end{align}
をつかって
(z_1^{(1)},z_2^{(1)}) =(h(a_1^{(1)}),h(a_2^{(1)}))
とします。さらにこの$z_1^{(1)},z_2^{(1)}$たちをもう一度、
\begin{align}
a_1^{(2)} &= 0.5z_1^{(1)} + 0.5z_2^{(1)} -0.7\\
&= (z_1^{(1)} ,z_2^{(1)})
\begin{pmatrix}
0.5\\
0.5
\end{pmatrix}
-0.7\\
z_1^{(2)}&=h(a_1^{(2)})
\end{align}
ってANDと$h$にかけて、「$z_1^{(2)}$」を得ることができます。
図にしてみると
わかりにくいので、処理の流れを図にしてみると下記のようになります。
さてさて、じつはこの 「$(x_1,x_2)→z_1^{(2)}$」 への演算がXORとなっています。
$(0,0),(1,1)$が$0$で、それ以外が$1$になってますね!
上記を描画するPythonのコードはこちら。
今回の図示は$h(\cdot)$ 演算も加味しているため階段状になっています(逆にいままでのNAND/OR/ANDは$h(\cdot)$ 演算前を図示していたので、平面 $f$ と$x,y$平面の上下関係で説明する図になってました。) が、たしかにXORを表現する演算になっていそうですね。。
Pythonで実際に確認
グラフ的にもただしくXORを出力できていそうですが、ホントにXOR演算になってるかな?ってことで、Pythonで計算します。書籍なかごろに出てくるニューラルネットワークのサンプルを応用します。
# !/usr/bin/env python
# -*- coding: utf-8 -*-
import sys
from abc import ABCMeta, abstractmethod
import numpy as np
def main(args):
x_test = np.array([
[0, 0],
[1, 0],
[0, 1],
[1, 1]
])
# network = AND()
# print(network.predict(x_test))
# print('---')
#
# network = OR()
# print(network.predict(x_test))
# print('---')
network = XOR()
print(network.predict(x_test))
print('---')
# print(network.network['W1'])
# print(network.network['b1'])
# print(network.network['W2'])
# print(network.network['b2'])
class Gate(metaclass=ABCMeta):
def h(self, x):
return step_function(x)
@abstractmethod
def predict(self, x):
pass
class AND(Gate):
def __init__(self):
self.network = {}
self.network['W1'] = np.array([[0.5], [0.5]])
self.network['b1'] = np.array([-0.7])
def predict(self, x):
W1 = self.network['W1']
b1 = self.network['b1']
a1 = np.dot(x, W1) + b1
z1 = super().h(a1)
return z1
class OR(Gate):
def __init__(self):
self.network = {}
self.network['W1'] = np.array([[0.5], [0.5]])
self.network['b1'] = np.array([-0.2])
def predict(self, x):
W1 = self.network['W1']
b1 = self.network['b1']
a1 = np.dot(x, W1) + b1
z1 = super().h(a1)
return z1
class NAND(Gate):
def __init__(self):
self.network = {}
self.network['W1'] = np.array([[-0.5], [-0.5]])
self.network['b1'] = np.array([0.7])
def predict(self, x):
W1 = self.network['W1']
b1 = self.network['b1']
a1 = np.dot(x, W1) + b1
z1 = super().h(a1)
return z1
class XOR(Gate):
def __init__(self):
self.network = {}
self.network['W1'] = np.array([[-0.5, 0.5], [-0.5, 0.5]])
self.network['b1'] = np.array([0.7, -0.2])
self.network['W2'] = np.array([[0.5], [0.5]])
self.network['b2'] = np.array([-0.7])
def predict(self, x):
W1 = self.network['W1']
W2 = self.network['W2']
b1 = self.network['b1']
b2 = self.network['b2']
a1 = np.dot(x, W1) + b1
z1 = super().h(a1)
a2 = np.dot(z1, W2) + b2
z2 = super().h(a2)
return z2
def step_function(x):
"""
やってることは
if x <= 0:
return 0
elif x > 0:
return 1
だけど、np.arrayを引数に取れるバージョン
:param x:
:return:
"""
return np.array(x > 0, dtype=np.int)
if __name__ == "__main__":
main(sys.argv)
さて実行する前に、Pythonの分離環境の作成と使用するライブラリを入れます。
$ sw_vers
ProductName: Mac OS X
ProductVersion: 10.14.4
BuildVersion: 18E226
$
$ python --version
Python 3.7.1
$ python -m venv ./venv
$ source ./venv/bin/activate
(venv) $
(venv) $ pip install numpy
(venv) $
さてさて、先のコードを実行してみます。
(venv) $ python perceptron_reg.py
[[0]
[1]
[1]
[0]]
---
(venv) $
おお、入力値:
x_test = np.array([
[0, 0],
[1, 0],
[0, 1],
[1, 1]
])
に対して、出力値: [0],[1],[1],[0] が得られたので、よさそうですね!
コードの説明
主要な部分だけコードを見てみます。まずXORクラスのコンストラクタで
def __init__(self):
self.network = {}
self.network['W1'] = np.array([[-0.5, 0.5], [-0.5, 0.5]])
self.network['b1'] = np.array([0.7, -0.2])
self.network['W2'] = np.array([[0.5], [0.5]])
self.network['b2'] = np.array([-0.7])
とやって、二次元配列を初期化しています。数式的には、
NANDとORに対応
\begin{align}
W1&=
\begin{pmatrix}
-0.5 & 0.5\\
-0.5 & 0.5
\end{pmatrix}\\
b1&= (0.7,-0.2)
\end{align}
ANDに対応
\begin{align}
W2&=
\begin{pmatrix}
0.5 \\
0.5
\end{pmatrix}\\
b2&= (-0.7)
\end{align}
となっていますね。
つづいて、値を計算して出力するメソッドはdef predict(self, x) です。
def predict(self, x):
W1 = self.network['W1']
W2 = self.network['W2']
b1 = self.network['b1']
b2 = self.network['b2']
a1 = np.dot(x, W1) + b1
z1 = super().h(a1)
a2 = np.dot(z1, W2) + b2
z2 = super().h(a2)
return z2
インスタンス変数に格納しておいたW1,W2,b1,b2を使って、
- NumPyを利用して行列の積と平行移動:
a1 = np.dot(x, W1) + b1を行う。 - その結果を関数
super().h(a1)にかける。(super().h(a1)は親クラスで、中でstep_function(a1)を呼んでいます)
を(計2回)繰り返して、結果を返しています。
メインの処理では
x_test = np.array([
[0, 0],
[1, 0],
[0, 1],
[1, 1]
])
network = XOR()
print(network.predict(x_test))
とやって、4つのインプットデータを一度に処理しています。python(というかNumPy)は、この行列処理が数学的でとても便利ですね。
以上で、行列の計算と関数$h$にかける処理の説明は以上です。
このコードから分かるとおり、入力や出力の次元を変えたければ、W1,W2などの行列の形をその通りに拡張すればよさそうです。また、今回は2回(NAND/OR → AND)だけの処理でしたが、繰り返したければW3,W4,..と定義していけばよさそうですね。
行列による一般化。
さてさて、先ほどでてきた
\begin{align}
(a_1^{(1)},a_2^{(1)}) &=( -0.5x_1 - 0.5x_2 +0.7,\ \ \ 0.5x_1 + 0.5x_2 -0.2) \\
&= (x_1,x_2)
\begin{pmatrix}
-0.5 & 0.5\\
-0.5 & 0.5
\end{pmatrix}
+(0.7,-0.2)
\end{align}
ですが、 Pythonのソースコードにもあらわれていましたが、
\begin{align}
\boldsymbol{x}&:=(x_1,x_2)\\
\boldsymbol{a^{(1)}}&:=(a_1^{(1)},a_2^{(1)})\\
W^{(1)} &:=
\begin{pmatrix}
-0.5 & 0.5\\
-0.5 & 0.5
\end{pmatrix}\\
\boldsymbol{b^{(1)}} &:=(0.7,-0.2)\\
\end{align}
と定義することで、
\boldsymbol{a^{(1)}} = \boldsymbol{x}\cdot W^{(1)} + \boldsymbol{b^{(1)}}
と、いわゆる一次変換(平行移動 $\boldsymbol{b^{(1)}}$ があるのでただしくはアフィン変換)で記述することが可能です。そして、成分表示がきえて $\boldsymbol{x}$ というベクトル表記になったことで、入力の$(x_1,x_2)$という2次元の入力が、$n$次元の入力へ容易に拡張可能になりました。
ようやくニューラルネットワークの話
いったん整理
さて、いままでの演算とくにXORの空間図形を見れば分かるとおり、$(x_1,x_2)$に対して、
- 空間上の平面 $z = w_1\cdot x_1+w_2\cdot x_2+ b$ 上のデータを生成
- それらに対して、上記の階段関数 $h(\cdot)$を合成する
- これらの演算を、複数回(XORは、NAND/OR で1回、そのあとAND で計2回) 繰り返す
とやることで、
という、直線では実現できない(これを線形分離が不可というみたい)分類が可能となりました。
さきほどの言い方をつかうと、XORは「2次元の入力に対して一次変換で2次元を出力して階段関数$h$にかけ、その出力された2次元を入力にさらに一次変換で1次元を出力して階段関数$h$にかける」ってことになります。
ニューラルネットワークとは
これを一般化すると「$n$次元の入力から、一次変換(アフィン変換)で$m$次元を出力して関数$h$にかけ、それをさらに入力に... と繰り返して、最終的に$l$次元の出力を得る」 事が出来ますね。
このように「行列の一次変換」と「ある関数$h$にくぐらせる」を繰り返すことで出力を得る機構の事をニューラルネットワークと呼びます。
さてニューラルネットワークを使った例としては、
- 手書きの画像データ 784次元の入力情報から(784→50→100→10と経て)最終的に 10次元のデータを出力して、0,1..,9の数字として「分類」する(MNISTの手書き認識)
- $x,y$平面上の$x$のデータ1次元を入力に(1→1と経て)1次元のデータを出力。出力した数値を予測値として「回帰」する(線形回帰)
- $x,y$平面上の$x$のデータ1次元を入力に(1→30→1と経て)1次元のデータを出力。出力した数値を予測値として「回帰」する(非線形回帰)
- $x,y,z$空間上の$(x,y)$のデータ2次元を入力に(2→1と経て)1次元のデータを出力。出力した数値を予測値として「回帰」する(重回帰)
などがあります。ニューラルネットワークが分類や回帰につかえるよ、ってのはこういうことですね。
また、入力・出力のレイヤーを**「入力層」「出力層」といい、計算過程の途中の50,100,30次元のレイヤーのことを「隠れ層」**と呼びます。
活性化関数
ある関数$h$、ってさきほど階段関数って書いてあったところをボヤかしてるのは、それを別の関数に変えることで、別の出力を得たりするからです。この$h$のことを「活性化関数」と呼びます。
この活性化関数ですが、XORで用いたように$0$ or $1$ を階段上に出力するのではなく、なだらかなデータを出力するためとか、いろいろな理由で別の関数を適用したりします。
例1:シグモイド関数
なだらかなデータを出力するために下記のシグモイド関数を用いることがあります。
h(x):=\frac{1}{1 + \exp(-x)}
シグモイド関数を$x,y$平面上で図示すると、
なるほど「階段関数($x=0$を境に$y=0 or 1$)をなだらかにした」ってイメージが伝わるかもしれません。
ちなみに、さきほどのXORの階段関数だった$h$をシグモイドにかえてみると、、、
こんな、なだらかな出力を得ることが出来ました。XORをシグモイドに替える幾何的な意味はあんまなさそうですが、さきほどの例で出したMNISTの画像認識や、非線形回帰などで線形でない出力を得たいときなどにシグモイドを用いたりするようです。
例2:ソフトマックス関数
分類を行うときの出力層における活性化関数に、下記のソフトマックス関数などを用いたりします。
y_k := \frac{\exp(a_k)}{\sum_{i=1}^{n}\exp(a_k)}
($y_k$ とは出力層が$n$次元データだとして、$k$番目の出力のこと)
$y_1,\cdots,y_n$ を全て足すと1になるので、出力値を確率としてあつかうときに適用します。
ようは活性化関数を何にするかは、分類か回帰か、隠れ層か出力層かなど、適材適所で使い分けるようです。
ニューラルネットワークの行列の値を決める方法、教師データの学習について
さてOR〜XORまでやってみて、
\boldsymbol{a^{(1)}} = \boldsymbol{x}\cdot W^{(1)} + \boldsymbol{b^{(1)}}
コレと活性化関数をなんども合成したものがニューラルネットワークだとしました。この
\begin{align}
W^{(l)} &:=
\begin{pmatrix}
w_{11}^{(l)} & w_{21}^{(l)} &\cdots &w_{m1}^{(l)}\\
w_{12}^{(l)} & w_{22}^{(l)} &\cdots &w_{m2}^{(l)}\\
\vdots & \ddots & w_{jk}^{(l)} & \vdots \\
w_{1n}^{(l)} &\cdots &\cdots &w_{mn}^{(l)}
\end{pmatrix}\\
\boldsymbol{b^{(l)}} &:=(b_1^{(l)},b_2^{(l)},\cdots,b_j^{(l)},\cdots,b_m^{(l)})\\
\end{align}
($l$は、$l$層目の隠れ層って意味)
これら$W^{(l)}$と$\boldsymbol{b^{(l)}}$ をそれぞれ重みとバイアス といいます。はじめにORをプロットしたときに突然
0.5x + 0.5y -0.2
つまり$w_1=0.5,w_2=0.5,b=-0.2$がエイヤって出てきましたが、実際は膨大なデータを処理させて、それらがよい出力を得られるように重みとバイアスの値を微調整していく必要があり、その調整のことを**「教師ありデータによるニューラルネットワークの学習」**といいます。
この辺は、正解とネットワークの出力値(予測値)の誤差を計測する**「損失関数」**(線形回帰の最小二乗法における「平均二乗誤差」みたいなモン) を定義して、それを最小化する問題に帰着させるのですが、今回は記事の長さの都合上、省略します。
参考: 「機械学習にでてくる勾配降下法/勾配ベクトルなどの整理。ついでにPythonで試してみた。」 に、「勾配降下法/勾配ベクトル」などについてちょっとだけ記事にしました。。
活性化関数 までふくめて定式化
もうすこし頑張ってみます。つづいて活性化関数まで含めてニューラルネットワークを定式化します。
\begin{align}
W^{(l)} &:=
\begin{pmatrix}
w_{11}^{(l)} & w_{21}^{(l)} &\cdots &w_{m1}^{(l)}\\
w_{12}^{(l)} & w_{22}^{(l)} &\cdots &w_{m2}^{(l)}\\
\vdots & \ddots & w_{jk}^{(l)} & \vdots \\
w_{1n}^{(l)} &\cdots &\cdots &w_{mn}^{(l)}
\end{pmatrix}\\
\boldsymbol{b^{(l)}} &:=(b_1^{(l)},b_2^{(l)},\cdots,b_j^{(l)},\cdots,b_m^{(l)})\\
\end{align}
($l$は、$l$層目の隠れ層って意味) とおいて、そして活性化関数を $h(\cdot)$ としたとき、
\begin{align}
\boldsymbol{z^{(l-1)}} &:=(z_1^{(l-1)},z_2^{(l-1)},\cdots,z_k^{(l-1)},\cdots,z_n^{(l-1)}) \\
\boldsymbol{z^{(l)}} &:=(z_1^{(l)},z_2^{(l)},\cdots,z_j^{(l)},\cdots,z_m^{(l)})
\end{align}
について
\boldsymbol{z^{(l)}} = h \biggl( \boldsymbol{z^{(l-1)}}\cdot W^{(l)} + \boldsymbol{b^{(l)}} \biggr)
と記述することができます。(いちおうですが、$l=1$のときの$n$が入力データの次元、さいごの$l$のときの$m$が出力データの次元、となるわけですね。)
ある $j$ 番目の要素を真剣に記述すると $(j=1,2,\cdots,m)$
z_j^{(l)} = h \biggl( \sum_{k=1}^{n} w_{jk}^{(l)}z_k^{(l-1)} + b_j^{(l)} \biggr)
うーん、もはやなんのこっちゃですが、、ようするにこうなります :-)
添え字が逆じゃないのかな?について
上記に記述したニューラルネットの重み行列の定義:
\begin{align}
W^{(l)} &:=
\begin{pmatrix}
w_{11}^{(l)} & w_{21}^{(l)} &\cdots &w_{m1}^{(l)}\\
w_{12}^{(l)} & w_{22}^{(l)} &\cdots &w_{m2}^{(l)}\\
\vdots & \ddots & w_{jk}^{(l)} & \vdots \\
w_{1n}^{(l)} &\cdots &\cdots &w_{mn}^{(l)}
\end{pmatrix}\\
\end{align}
ですが、$W^{(l)}$の添え字($ij$)が、普通の数学と逆なんですよね。なんでかなって思ってたんですが「ニューラルネットワークの出力の行列を用いた高速な計算(ページ内を「奇妙」で検索)」をみることでわかりました。
既出の**$j$ 番目の要素を記述している数式:**
z_j^{(l)} = h \biggl( \sum_{k=1}^{n} w_{jk}^{(l)}z_k^{(l-1)} + b_j^{(l)} \biggr)
**は、$\boldsymbol{z^{(l)}}$ や$\boldsymbol{b^{(l)}}$ を縦ベクトルで記述する流派(?)からすると 、$W^{(l)}$を転置した行列をあらためて$W^{(l)}$**と記述することで、
\boldsymbol{z^{(l)}} = h \biggl( W^{(l)} \boldsymbol{z^{(l-1)}} + \boldsymbol{b^{(l)}} \biggr)
と書くことができます。ここで、
\begin{align}
W^{(l)} :=
\begin{pmatrix}
w_{11}^{(l)} & w_{12}^{(l)} &\cdots &w_{1n}^{(l)}\\
w_{21}^{(l)} & w_{22}^{(l)} &\cdots &w_{2n}^{(l)}\\
\vdots & \ddots & w_{jk}^{(l)} & \vdots \\
w_{m1}^{(l)} &\cdots &\cdots &w_{mn}^{(l)}
\end{pmatrix}
, \
\boldsymbol{b^{(l)}} :=\left(
\begin{array}{c}
b_1^{(l)}\\
b_2^{(l)}\\
\vdots\\
b_j^{(l)}\\
\vdots\\
b_m^{(l)}
\end{array}
\right)
\end{align}
\begin{align}
\boldsymbol{z^{(l)}} =
\left(
\begin{array}{c}
z_1^{(l)}\\ z_2^{(l)}\\ \vdots\\z_j^{(l)}\\ \vdots\\ z_m^{(l)}
\end{array}
\right)
\end{align}
, \ \
\boldsymbol{z^{(l-1)}} =
\left(
\begin{array}{c}
z_1^{(l-1)}\\z_2^{(l-1)}\\ \vdots\\ z_k^{(l-1)}\\ \vdots \\ z_n^{(l-1)}
\end{array}
\right)
です。添え字が逆の理由はたぶんコレではないかと。。成分表示をしている時の計算では、$W$の添え字がどっちなのかな?ベクトルが縦か横かどっちなのかな?なんてのを気にする必要がありそうです。
ニューラルネットワークを用いたサンプル
ニューラルネットワークを用いてどんな事が出来るかについて、具体的なサンプルを紹介したいと思います。たとえば、$x,y$平面におけるプロットの線形回帰や非線形回帰、またMNISTの手書き数字を$0〜9$いずれかに分類するなど、をコードとともにQiitaに記事にしようと思いますが、でき次第リンクをつけようと思います。いったん、とりあえずキャプチャだけのせます。
線形回帰
$x,y$平面におけるプロットについて、入力層が1次元、出力層が1次元、隠れ層なしのニューラルネットワークを用いて回帰を行っています。ニューラルネットワークの出力をそのまま予測値として使用するため、出力層の活性化関数は恒等関数(ようするに何もしない)にしています。
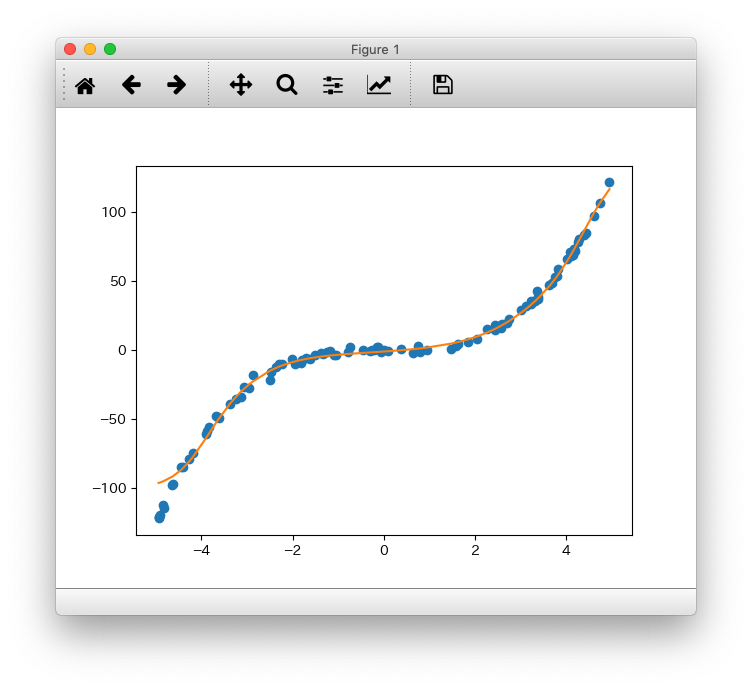
非線形回帰
$x,y$平面におけるプロットについて、入力層が1次元、出力層が1次元、隠れ層が3次元のニューラルネットワークを用いて回帰を行っています。ニューラルネットワークの出力をそのまま予測値として使用するため、出力層の活性化関数は恒等関数(ようするに何もしない)にしています。隠れ層の活性化関数はシグモイドを用いています。
MNISTの手書き認識
MNISTにて配布されている手書きデータを分類する有名なヤツです。
書籍のほぼそのままなのですが、MNISTに公開されている手書き数字を、入力層が、784次元、出力層が10次元、隠れ層が、50次元、100次元のニューラルネットワークを用いて分類しています。隠れ層の活性化にはシグモイドを用いていますが、出力層は「結果が、各分類0から9である確率(1x10の行列)」を出力するために、ソフトマックス関数を用いています。
参考:MNISTの手書き数字の画像セットを、視覚的に見てみる
長かったですね。。おつかれさまでした。
補足。XORの図をPythonで表示してみる
さきほどXORの図を図示しましたが、そのPythonのコードを貼っておきます。
描画にはmatplotlibを用いています。環境構築は下記の通りです。
$ sw_vers
ProductName: Mac OS X
ProductVersion: 10.14.4
BuildVersion: 18E226
$
$ python --version
Python 3.7.1
$ python -m venv ./venv
$ source ./venv/bin/activate
(venv) $
(venv) $ pip install numpy matplotlib PyQt5
(venv) $
参考: MacでMatplotlib がエラーが出たりプロットが表示されないときの対応
さてコード。
# !/usr/bin/env python
# -*- coding: utf-8 -*-
import sys
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
# def sigmoid(x):
# return 1 / (1 + np.exp(-x))
def step_function(x):
"""
やってることは
if x <= 0:
return 0
elif x > 0:
return 1
だけど、np.arrayを引数に取れるバージョン
:param x:
:return:
"""
return np.array(x > 0, dtype=np.int)
def h(x):
return step_function(x)
# return sigmoid(x)
def XOR_3d(X, Y):
n = NAND(X, Y)
n = h(n)
o = OR(X, Y)
o = h(o)
a = AND(n, o)
a = h(a)
return a
def perceptron(x1, x2, w1, w2, b):
return w1 * x1 + w2 * x2 + b
def AND(x1, x2):
# (1,1)(x1,x2) - 1.4 = 0 な直線
return perceptron(x1, x2, w1=0.5, w2=0.5, b=-0.7)
def NAND(x1, x2):
# (1,1)(x1,x2) - 1.4 = 0 な直線
return perceptron(x1, x2, w1=-0.5, w2=-0.5, b=0.7)
def OR(x1, x2):
# (1,1)(x1,x2) - 1.4 = 0 な直線
return perceptron(x1, x2, w1=0.5, w2=0.5, b=-0.2)
def main(args):
x = np.arange(-0.1, 1.1, 0.01)
y = np.arange(-0.1, 1.1, 0.01)
X, Y = np.meshgrid(x, y)
Z = XOR_3d(X, Y)
fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("f(x, y)")
# ax.plot_surface(X, Y, Z, alpha=0.3)
ax.plot_wireframe(X, Y, Z)
plt.show()
if __name__ == "__main__":
main(sys.argv)
関連リンク
-
MNISTの手書き数字の画像セットを、視覚的に見てみる
書籍のコードをすこしだけ解説。手書き認識(分類)にシグモイドとソフトマックス関数で確率を出力しています。 -
GeoGebra 数学アプリ
グラフを作成するツールを探している過程で、なんだかとんでもなく便利なアプリを見つけてしまいました。。。陰関数まで解釈して図示してくれてすごいっす。今回Python以外での描画はすべてこのアプリを使用しました。
-
あ、ちなみにXORを実装するにはNANDとORとANDを駆使すればよいっていう回路の知識を前提としています。 ↩