最近話題のED法、色々見ても理解できなかったのでRustで再実装してみました。
かなりED法のコンセンプトをわかりやすく実装に落とし込めた気がします。
そしてやはり静的型付け言語はいい…読みやすい…
試しに二乗誤差以外の損失関数も使えるか試したところ、BCELossでも(BCEWithLogitsLossでも)学習がうまく行ったので共有します。
実行結果
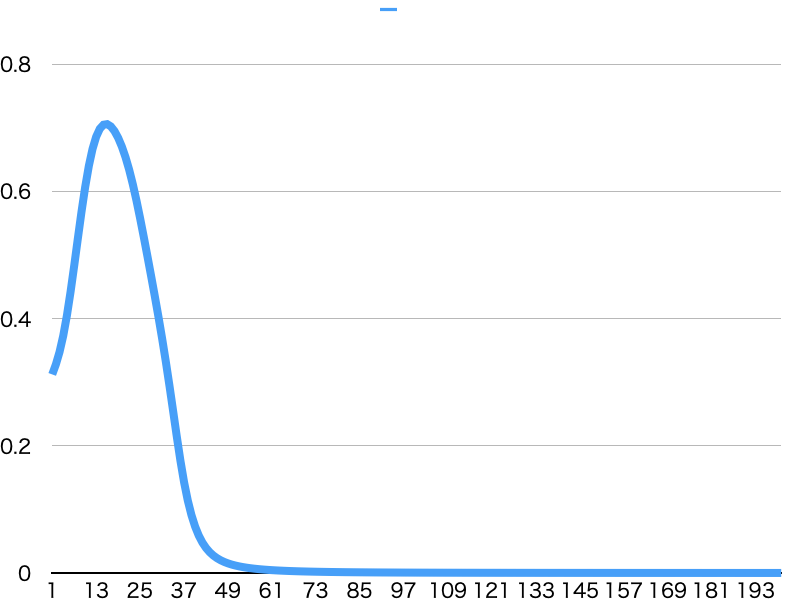
MSELoss
いい感じに学習ができています。
省略
loss: 0.00007618
loss: 0.00007514
loss: 0.00007413
loss: 0.00007313
loss: 0.00007216
0, 0 -> 0.01357774, 0
0, 1 -> 0.99463046, 1
1, 0 -> 0.99464429, 1
1, 1 -> 0.00611493, 0
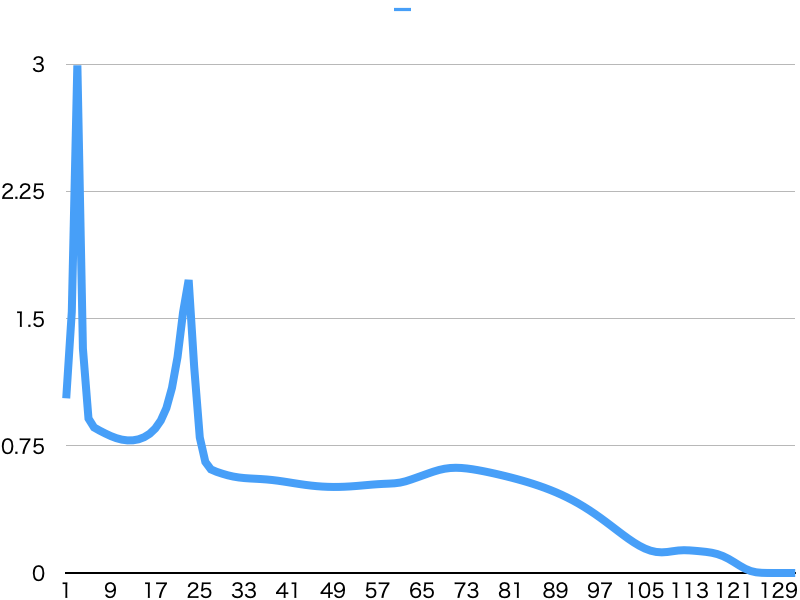
BCELoss
下降が安定はしないものの、100回程度の学習で損失値がほぼ0になりました。
省略
loss: 0.00002283
loss: 0.00000227
loss: 0.00000019
loss: 0.00000001
loss: 0.00000000
0, 0 -> 0.00000000, 0
0, 1 -> 1.00000000, 1
1, 0 -> 1.00000000, 1
1, 1 -> 0.00000000, 0
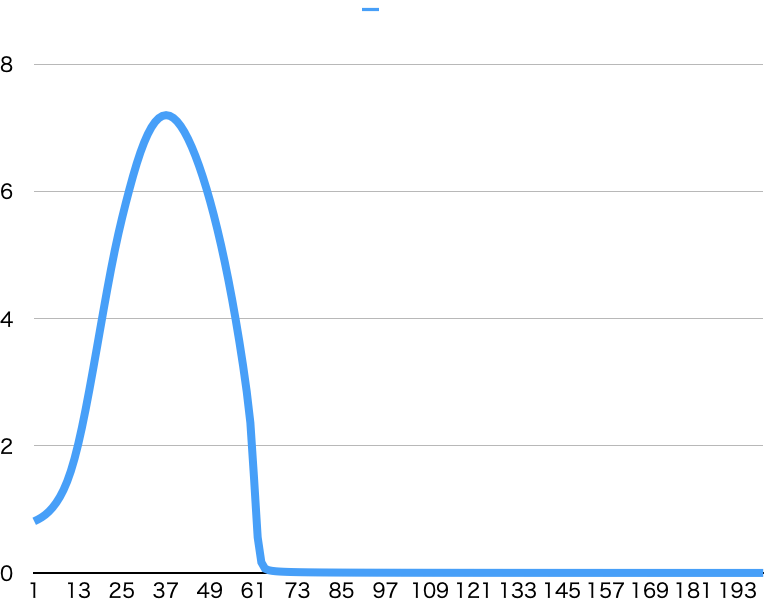
BCEWithLogitsLoss
やはりBCELossより安定しています。
MSELossと同じ回数の学習で精度が良くなっています。
学習率とか最適化していないので偶然かもしれませんが。
省略
loss: 0.00117913
loss: 0.00117034
loss: 0.00116168
loss: 0.00115314
loss: 0.00114473
loss: 0.00113644
0, 0 -> 0.00362398, 0
0, 1 -> 0.99954242, 1
1, 0 -> 0.99958153, 1
1, 1 -> 0.00000000, 0
実装解説
Neuron
興奮性ニューロンか抑制性ニューロンのいずれかを表します。
1つの値を受け取り1つの値を出力します。
SingleOutputLayer
N個のニューロンを持ちます。N個の値を受け取り、1個の値を出力します。
興奮性ニューロンと抑制性ニューロンを互い違いに持っています。
逆伝播(って言ったら怒られるか)の実装が特徴的で、自分自身への入力と最終アウトプットの勾配のみから学習を行うことができています。
fn backward(&mut self, delta: f64, last_inputs: &Vec<f64>) {
let delta = ActivationFunc::derivative(self.last_output) * delta;
for (i, neuron) in self.neurons.iter_mut().enumerate() {
if delta < 0. {
if i % 2 == 0 {
neuron.append_weight(delta * last_inputs[i]);
}
} else {
if i % 2 == 1 {
neuron.append_weight(-delta * last_inputs[i]);
}
}
}
}
Layer
M個のSingleOutputLayerを持ちます。全てのSingleOutputLayerは同一のN個のニューロンを持っています。
N個の値を受け取り、M個の値を出力します。
SingleOutputLayer同士のニューロンも互い違いになっています。
学習は、保存しておいた自分自身への入力と勾配をSingleOutputLayerにぶん投げているだけです。
pub fn backward(&mut self, delta: f64) {
for layer in self.inner_layers.iter_mut() {
layer.backward(delta, &self.last_inputs);
}
}
Gate
2つの値を受け取り1つの値を返すゲートを学習するモデルです。
慣れ親しんだpytorch風に実装しました。
なんといってもわかりやすく名前をつけたbackwardが全然backwardじゃないのが気に入っています。
pub struct Gate<LastActivation>
where
LastActivation: DifferentiableFn<Args = f64>,
{
layer0: Layer<Sigmoid>,
layer1: Layer<Sigmoid>,
layer2: Layer<LastActivation>,
}
impl<LastActivation> Gate<LastActivation>
where
LastActivation: DifferentiableFn<Args = f64>,
{
pub fn new() -> Self {
let mut rng = StdRng::seed_from_u64(42);
Gate {
layer0: Layer::new(&mut rng, 4, 8),
layer1: Layer::new(&mut rng, 8, 8),
layer2: Layer::new(&mut rng, 8, 1),
}
}
pub fn forward(&mut self, inputs: &[f64]) -> f64 {
let x = vec![inputs[0], inputs[0], inputs[1], inputs[1]];
let x = self.layer0.forward(x);
let x = self.layer1.forward(x);
self.layer2.forward(x)[0]
}
pub fn backward(&mut self, delta: f64) {
self.layer0.backward(delta);
self.layer1.backward(delta);
self.layer2.backward(delta);
}
}
今回の再実装での学び
- ED法では層を遡らなくても重みを更新できる
- 重みの更新に必要な引数は以下の3つ
- 自分自身の引数
- 活性化関数の微分関数
- 損失値
- 重みの更新方法以外は通常の全結合層と変わらない
- 元実装にあるbetaはなくても学習できる
- 元実装のsigmoidはちょっと変だけど、普通のsigmoidで問題ない
- Cの元実装を追うのはC言語読み慣れないのもあってとてもしんどい
所感
自分自身への入力値と損失値だけあれば重みを更新できるというのはSNNを知らなかった自分からすると革命的でした。
複数の値の出力を持つモデルの学習は厳しいという考察があり、自分もそのような所感を持っていますが、金子さんはNekoFightをED法で学習していたわけで、なにか方法がありそうな気がしています。
そこさえクリアできれば、単純に全結合層をつなげただけのモデルであらゆる入出力に対して超多層学習が可能になり、夢が広がります。
ただ、色々試してもバッチでの学習がうまくいかず、そこも課題になりそうです。
まだ数学的な理解が追いついていませんが、一過性の盛り上がりで終わらずに研究が進むことを期待しています。
参考
元実装
旅の始まり
発見者