金子勇さんのED法の解説と弱点、行列積を使用した効率的な実装

はじめに

先日以下の記事が話題となり、とてもワクワクしたので自分も実装して色々実験してみました。

実装するうちに理解が深まったので一度、

• 誤差拡散法の元ネタ紹介から
• 数式の解説、
• ED法の弱点、
• 行列計算を使用した実装と簡単なテスト結果、
• 実装上の工夫

までまとめてみたいと思います。

誤差拡散（Error Diffusion）法

もともとは画像の2値化において失われる情報を周囲のピクセルで補うことで、遠目に元の画像の濃淡が残っているように見せる技術（ハーフトーン処理の一種）です。
Error diffusion -Wikipedia（英語版）

左の画像をちょうど半分の明るさをしきい値として2値化すると中央の画像のようになりますが、誤差拡散法を適用すると2値化後も右の画像のようにある程度濃淡を保存・表現できます。

誤差拡散法（画像処理）のサンプルコード

コメントアウト箇所はFloyd, Steinbergらのカーネル、非コメントアウト状態（そのまま）のものはJF Jarvis, CN Judice, WH Ninkeらのカーネル

import matplotlib.pyplot as plt
from io import BytesIO
from requiests import get

url = "https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg2dvuvi_VSVGkzORLeRYSzJid_WnW87vr8evE0R3UsfUvf-Mp5A9Ck5A6z5Nf8MwklomuG4s8lBtqE0EMieboxTAhyphenhyphenXzN8OGY_DfnFhsA_adweiu-CyYNWHRPrEf9rQ2C2-FAl6h2cTJfB/s800/ai_study_kikaigakusyu.png"
im = plt.imread(BytesIO(get(url).content))[..., 1]
if im.dtype == np.uint8:
    im = im.astype(float) / 255

h, w = im.shape
# karnel = np.array([[0, 0, 7], [3, 5, 1]]) / 16
karnel = np.array([[0, 0, 0, 7, 5], [3, 5, 7, 5, 3], [1, 3, 5, 3, 1]]) / 48
bi = (im > .5) * 1.
error = im - bi
edim = np.zeros(im.shape)
for i in range(h):
    for j in range(w):
        edim[i, j] = (bi[i, j]+error[i, j]) > .5
        e = (im[i, j] - (bi[i, j]+error[i, j] > .5)) * karnel
#         for di, dj in [[0, 1], [1, -1], [1, 0], [1, 1]]:
        for di, dj in [[0, 1], [0, 2], [1, -2], [1, -1], [1, 0], [1, 1], [1, 2], [2, -2], [2, -1], [2, 0], [2, 1], [2, 2]]:
            if 0<=i+di<h and 0<=j+dj<w:
#                 error[i+di, j+dj] += e[di, dj+1]
                error[i+di, j+dj] += e[di, dj+2]

plt.imshow(edim, cmap="gray")
plt.show()

誤差をあらかじめ決まった割合で周りのピクセルに伝搬させるイメージが共通することからED法？

NN更新手法としてのED法

生物学的・脳科学的な解釈は一旦置いておいて、ED法を簡単に説明すると、
出力を増加させる部分と低下させる部分とを分担することで、出力層から遡っての勾配計算（誤差逆伝播）を省略してパラメータを更新することを可能にするというものです。
出力が正解より大きければ出力を低下させる部分を更新して、
出力が正解より小さければ出力を増加させる部分を更新する。
それだけです。
誤差逆伝播（バックプロパゲーション／BP）を必要としないので、前の層を待たずに値を更新できることから、並列処理と相性が良さそうです。

上記の説明で勘の良い方はお気づきかもしれませんが、金子勇さんのED法ではパラメータの絶対値は常に増加するように更新します。

数式を使った説明

金子勇さんのHPに倣うと、

誤差逆伝播法と共通部分

各細胞（ノード）の入出力を以下のように表します。添字$k$は層の番号です。

\begin{align}
i^k_j=\sum_{i}{w^k_{ij}o^{k-1}_i}\tag{1}\\
o^k_i=f(i^k_i)\tag{2}
\end{align}

$f$は活性化関数で、ここではシグモイド関数を使用しています。
$$
f(x) = \frac{1}{1+\exp{(-2x/u_0)}}\tag{3}
$$

モデルの出力を１つとすると、2乗誤差は
$$
r=\frac{1}{2}\left(y-o^m\right)^2 \tag{4}
$$
となります（？）（画像が消えているため後の偏微分からの推測）。
$k-1$層の$i$番目の細胞から$k$層の$j$番目の細胞への入力の重みパラメータを$w^k_{ij}$のように書き表すと、誤差$r$を減らすには学習率$\alpha$を用いて、

$$
\Delta w^k_{ij} = -\alpha \frac{\partial r}{\partial w^k_{ij}} \tag{5}
$$

のように更新すればよいです。

\begin{align}
\begin{split}
-\frac{\partial r}{\partial w^k_{ij}} &= -\frac{\partial r}{\partial o^k_j}\frac{\partial o^k_j}{\partial i^k_j}\frac{\partial i^k_j}{\partial w^k_{ij}}\\ 
&=-\frac{\partial r}{\partial o^k_j}f'\left(o^k_j\right)o^{k-1}_i
\end{split}\tag{6}
\end{align}

であるので、 ¹

$$
\Delta w^k_{ij} = -\alpha \frac{\partial r}{\partial w^k_{ij}}=\alpha \frac{\partial r}{\partial o^k_j}f'\left(o^k_j\right)o^{k-1}_i\tag{7}
$$

ここで、$f'$は活性化関数の微分で、シグモイド関数の場合

$$f'(x)=f(x)\left(1-f(x)\right)$$

です。

残る偏微分ですが特に出力層（$k=m$）層において式(4)より、
$$\frac{\partial r}{\partial o^m}=\frac{\partial}{\partial o^m}\left[\frac{1}{2}\left(y-o^m\right)^2\right]=o^m-y\tag{8}$$
となります。
これの符号を反転したもの
$$d^m=-\frac{\partial r}{\partial o^m}=y-o^m\tag{9}$$
を$d^m$と置いておきます。

ここまでは、誤差逆伝播法と共通です。

ED法独自のアプローチ

ED法では、先ほど定義した$d^m$をアミン（神経伝達物質）の分泌濃度と解釈し、すべての細胞（ノード）間の重みはこのアミン濃度$d^m$に比例して更新（＝結合の強化）されます。

前節では、出力を増加させる部分と低下させる部分が独立して存在していると説明しました。
これを金子勇さんはこれらを神経細胞になぞらえて、興奮性細胞・抑制性細胞と呼んでいます。
そして、興奮性細胞からの接続の強化を促進するアミンを$d^{m+}$、
抑制性細胞からの接続の強化を促進するアミンを$d^{m-}$としています。

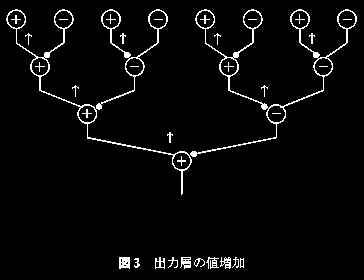
出典：https://web.archive.org/web/20000306212433/http://village.infoweb.ne.jp:80/~fwhz9346/ed.htm

金子勇さんのモデルでは出力層は興奮性細胞と設定しています。
興奮性細胞は出力を増加させるため、出力が正解より小さい場合、すなわち$y-o^m>0$のときには、より他の興奮性細胞との結合を強めるように値を更新します。
つまり、$d^{m+}$を分泌すればよいため、

\begin{align}
\begin{split}
d^{m+}&=y-o^m\\
d^{m-}&=0
\end{split}\tag{10}
\end{align}

逆に出力が正解より大きい$y-o^m<0$のときには、より抑制性細胞との結合を強めるように値を更新します。

\begin{align}
\begin{split}
d^{m+}&=0\\
d^{m-}&=o^m-y
\end{split}\tag{11}
\end{align}

このとき、結合を強める＝常に重みの絶対値は増加する方向にのみ更新されます。

次に出力層以外の$d^k$ですが、アミンが拡散し空間を伝って（ネットワークを逆行してではなく）直接各細胞に伝わる様子を表現して、すべての層において単に$d^m$に減衰率$u_1$をかけた、

\begin{align}
\begin{split}
d^{k+}&=u_1d^{m+}\\
d^{k-}&=u_1d^{m-}
\end{split}\tag{12}
\end{align}

とします。

以上をまとめると最終的に学習則は式(7)よりそれぞれ、
興奮性細胞からの結合の場合、

\Delta w^k_{ij}=\alpha d^{k+}_jf'\left(o^k_j\right)o^{k-1}_isign\left(w^k_{ij}\right) \tag{13}

抑制性細胞からの結合の場合、

\Delta w^k_{ij}=\alpha d^{k-}_jf'\left(o^k_j\right)o^{k-1}_isign\left(w^k_{ij}\right) \tag{14}

となります。
ただし、興奮性細胞は出力の増加に寄与、抑制性細胞はその逆という関係を満たすために、
k-1 層 i 番目の細胞と k 層 j 番目の細胞が同種の場合
$$w^k_{ij}\ge0\tag{15}$$
k-1 層 i 番目の細胞と k 層 j 番目の細胞が異種の場合
$$w^k_{ij}\le0\tag{16}$$
の関係を満たす必要があります。

式(13)(14)より、ED法では誤差を逆伝播しなくとも最終的な出力と各細胞のローカルな勾配のみで値を更新することができるため、勾配消失などの問題が発生せず幾らでも層を重ねることが可能となります。

ED法の弱点

複数出力ができない問題

ED法では、出力の増減とに応じてすべての細胞が画一的に更新されるため、出力が1つの場合には学習が早いのですが、複数値の出力になった途端に学習ができなくなる感触です。
というのも、誤差逆伝播法ではどの出力にどのパラメータがどの程度寄与しているのか知ることができますが、ED法では出力層の重み以外は、”どの重みがどの出力への寄与が大きい”などの情報は一切存在しないため当然といえば当然です。

対応策としては、1つの出力に1つのネットワークを用意するというのが一番シンプルですが、無駄が多いですし、他の出力との相互的な作用が考慮できません。

活性化関数が限定的

後ほどシグモイド関数以外も使用できる形の実装例を示しますが、シグモイド以外の活性化関数ではほとんどの場合うまく学習できません。

すべての細胞を画一的に更新するという大雑把さから繊細な調整が効かないことが原因として大きいと感じます。
指数が含まれる式は容易に発散しますし、ReLUは興奮性細胞では恒等関数、抑制性細胞ではただの0です。

また、同じ理由で連続値の出力も苦手そうです。

これらの問題を上手く回避してやらないと、一時のネタ以上の発展は難しそうです。

実装例

金子勇さんのホームページに本家サンプルコードがありますし、本家に忠実なPythonでの実装例も既に@pocokhc(ちぃがぅ)さんがあげてられているので、
私は層単位でまとめた、PyTorchのnn.Linearに近い実装をしてみようと思います。
層の入力計算はまとめて行列として行うので、幾らか（70倍程度）実行速度もマシなはずです。

いくつかの活性化関数たち

import numpy as np

def sigmoid(x, u0=.4):
    x *= 2 / u0
    return np.exp(np.minimum(x, 0)) / (1 + np.exp(- np.abs(x)))

def dsigmoid(x):
    return x * (1 - x)

sigmoid.d = dsigmoid

def relu(x):
    return np.maximum(0, x)

def drelu(x):
    return (x > 0) * 1

relu.d = drelu

def elu(x, a=1):
    y = x.copy()
    y[x<0] = a*(np.exp(x[x<0]) - 1)
    return y
    
def delu(x, a=1):
    return np.maximum(x + a, 1)

elu.d = delu

def softplus(x, u0=5):
    x = x / u0
    return (np.log1p(np.exp(-np.abs(x))) + np.maximum(x, 0)) / u0

def dsoftplus(x, u0=5):
    return 1 - np.exp(-abs(u0*x))

softplus.d = dsoftplus

バッチ学習と、一応複数出力にも対応しています。

import numpy as np

class Linear:
    def __init__(self, in_, out_):
        self.weight = np.random.rand(in_, out_)
        
    def __call__(self, x):
        return self.forward(x)
        
    def forward(self, x):
        self.input = x.copy()
        self.output = x @ self.weight
        return self.output

class ED_Layer:
    def __init__(self, in_, out_, alpha=.8, f=sigmoid):
        self.in_ = in_
        self.out_ = out_
        self.alpha = alpha
        self.f = f
        self.pp = Linear(in_, out_)
        self.np = Linear(in_, out_)
        self.pn = Linear(in_, out_)
        self.nn = Linear(in_, out_)
    
    def __call__(self, p, n):
        return self.forward(p, n) 
        
    def forward(self, p, n):
        self.op = self.f(self.pp(p) - self.np(n))
        self.on = self.f(self.nn(n) - self.pn(p))
        return self.op, self.on
    
    def update(self, d):
        for ope, l, o in ((1, self.pp, self.op), (-1, self.np, self.op), (1, self.pn, self.on), (-1, self.nn, self.on)):
            dw = np.einsum("b,bo,bi->bio", d.mean(1), self.f.d(o), l.input)
            l.weight += ope * self.alpha * dw.mean(0)
                
class ED_OutputLayer(ED_Layer):
    def __init__(self, in_, out_, alpha=.8, f=sigmoid):
        super().__init__(in_, out_, alpha, f)
        
    def update(self, d):
        for ope, l, o in ((1, self.pp, self.op), (-1, self.np, self.op), (1, self.pn, self.on), (-1, self.nn, self.on)):
            dw = np.einsum("bo,bo,bi->bio", d, self.f.d(o), l.input)
            l.weight += ope * self.alpha * dw.mean(0)
            
        
class ED:
    def __init__(self, in_, out_, hidden_width, hidden_depth=1, alpha=.8):
        self.layers = [
            ED_Layer(in_, hidden_width, alpha, sigmoid),
            *[ED_Layer(hidden_width, hidden_width, alpha, sigmoid) for _ in range(hidden_depth)],
            ED_OutputLayer(hidden_width, out_, f=sigmoid)
        ]
    
    def __call__(self, x):
        return self.forward(x)
    
    def forward(self, x):
        p, n = x.copy(), x.copy()
        for layer in self.layers:
            p, n = layer(p, n)
        return p
    
    def update(self, d):
        for layer in self.layers:
            layer.update(d)
            

定番XORテスト

中間層： 一層あたり 8*2（興奮/抑制）細胞、5層

np.random.seed(seed=1)
ed = ED(3, 1, 8, 5)

data = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
beta = .1
input_ = np.array([[beta, *a] for a in data])
y = data[:, 0] ^ data[:, 1]
for i in range(100):
    output = ed(input_)
    d = (y[:, None]-output)
    ed.update(d)
    
for i, j in [[0, 0], [0, 1], [1, 0], [1, 1]]:
    print(i^j, ed(np.array([[beta, i, j]])))

out

0 [[2.40317068e-08]]
1 [[1.]]
1 [[1.]]
0 [[2.40316328e-08]]

MNIST 0/1判定

データセット準備

import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms

train_dataset = torchvision.datasets.MNIST(root='./MNIST',
                                           train=True,
                                           transform=transforms.ToTensor(),
                                           download = True)
                                           
test_dataset = torchvision.datasets.MNIST(root='./MNIST',
                                           train=False,
                                           transform=transforms.ToTensor(),
                                           download = True)

class CustomMNISTDataset(torch.utils.data.Dataset):
    def __init__(self, data):
        self.data = data

    def __len__(self):
        return len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]
        
sub_train_dataset = [(img, label) for img, label in train_dataset if label in [0, 1]]
sub_test_dataset = [(img, label) for img, label in test_dataset if label in [0, 1]]

custom_dataset = CustomMNISTDataset(sub_train_dataset)
custom_dataset_v = CustomMNISTDataset(sub_test_dataset)

batch_size = 128

train_loader = torch.utils.data.DataLoader(dataset=custom_dataset,
                                           batch_size=batch_size,
                                           shuffle=True)

test_loader = torch.utils.data.DataLoader(dataset=custom_dataset_v,
                                           batch_size=batch_size,
                                           shuffle=True)

1層あたり 2*2 細胞、512層

学習

from tqdm import tqdm

ed = ED(28*28, 1, 2, 512, alpha=.2)
for _ in range(10):
    for i, (images, labels) in enumerate(tqdm(train_loader)):
        images = images.view(-1, 28*28).numpy()
        output = ed(images)[:, 0]
        err = labels.numpy() - output
        d = err[..., None]
        ed.update(d)

テスト

nims = 0
correct = 0
for images, labels in tqdm(test_loader):
    images = images.view(-1, 28*28).numpy()
    output = ed(images)[:, 0]
    nims += len(labels)
    correct += (output.round()==labels.numpy()).sum()
print(f"{(correct/nims)*100:.02f}%")

# 99.53%

そこそこ高い精度です。テスト時にはテストデータで100%出たこともありました。
ED法、2値分類には強そうです。
学習速度は1エポックあたり6秒程度でした（12665枚/ミニバッチサイズ128枚、Ryzen7 5700X）。
注目すべきは512層もの超深層学習が平然と行われている点です。
BP法では考えられない事態です。

余談ですが、モデルを10個並列して0~9の分類問題を行った結果は正答率93%程度でした。

実装上の工夫点の解説

層ごとに行列計算を行うために加えた工夫を簡単に解説します。

層を表現するクラス（ED_Layerクラス）

ある細胞への入力$i^k_j$は式(1)より次のように与えられるのでした。

\begin{align}
i^k_j=\sum_{i}{w^k_{ij}o^{k-1}_i}\tag{1}
\end{align}

結合の重み$w^k_{ij}$や前層の出力$o^{k-1}_{i}$を出力の細胞のタイプ（興奮/抑制）を明記して分けると上記の式は、

\begin{align}
i^k_j&=\sum_{i}{w^k_{ij}o^{k-1}_i}\tag{1}\\
&=\sum_{i+}{w^{k+}_{ij}o^{k-1+}_i}+\sum_{i-}{w^{k-}_{ij}o^{k-1-}_i}\tag{17}\\
&=i^{k+}_j+i^{k-}_j\tag{18}
\end{align}

と展開できます。
つまり、更新タイミングの異なる2つの重みを個別に管理することが可能です。

各層に必ず興奮性細胞と抑制性細胞が同数存在し、層間の細胞が全結合しているとすれば、
出入力の組み合わせは興奮-興奮、興奮-抑制、抑制-興奮、抑制-抑制の4通りあり、それぞれ同数ずつであることになります。
なので、ある1層を表現するクラスを作成するためには、

• これら4つの重み行列を保持して、
• 各々適切なタイミングで更新して、
• 入力値との行列計算結果を興奮出力/抑制出力でそれぞれ足し合わせて、
• 活性化関数を通して出力

できれば良さそうです。

重み更新の符号

上記で重みを個別に管理することにしたので、式(13)(14)の重みの更新方向を制限する符号部分$sign(w^k_{ij})$は式(18)の足し合わせの符号に押し付ける事ができます。
つまり、

\begin{align}
i^k_j&=i^{k+}_j+i^{k-}_j\tag{19}\\
&=sign(w^{k+}_{ij})\sum_{i+}{w^{k+}_{ij}o^{k-1+}_i}+sign(w^{k-}_{ij})\sum_{i-}{w^{k-}_{ij}o^{k-1-}_i}\tag{20}\\
&=\left\{
\begin{array}{ll}
\sum_{i+}{w^{k+}_{ij}o^{k-1+}_i}-\sum_{i-}{w^{k-}_{ij}o^{k-1-}_i} & (興奮性細胞)\\
\sum_{i-}{w^{k-}_{ij}o^{k-1-}_i}-\sum_{i+}{w^{k+}_{ij}o^{k-1+}_i} & (抑制性細胞)
\end{array}\tag{21}
\right.
\end{align}

\Delta w^k_{ij}=
\left\{
\begin{array}{ll}
\alpha d^{k+}_jf'\left(i^k_j\right)o^{k-1}_i & (興奮性細胞)\\
\alpha d^{k-}_jf'\left(i^k_j\right)o^{k-1}_i  & (抑制性細胞)
\end{array}\tag{22}
\right.

です。

重みの更新タイミング

出力を増やしたいときに抑制性細胞の結合を弱める方向の学習を行っても（その逆も然り）機能上問題なく、逆に重みの発散を抑制する効果が期待できるため、本実装では双方向に値更新を行っています。
そのため、$d^{m+}, d^{m-}$の区別も不要となり、
$$d^{m}=y-o^m$$
のみを使用しています。

（減衰率 u1の行方）

層ごとに分けて実装していることから、学習率$\alpha$と一緒くたに表現できるため省略しています。

更なる実装の簡易化・高速化（4/29追記）

ED法独自の更新方向の符号周りを限界までシンプルにまとめました（ED_Linearの初期化部分でほぼ完結）。
ここまでくれば既存のライブラリの使用等、応用もしやすそうです。
後で解説も足すかも。

↓その他の変更点

• 初期層以外にもバイアス項の追加
• 複数出力機能は結局学習できないでカット

import numpy as np

class ED_Linear:
    def __init__(self, in_, out_):
        self.weight = abs(np.random.randn(2, 2, in_, out_))
        self.bias = np.random.rand(2, 1, out_)
        self.weight[:, 1] *= -1
        self.ope = np.array([[[1]], [[-1]]])
        
    def __call__(self, x):
        return self.forward(x)
        
    def forward(self, x):
        return ((x @ self.weight).sum(1) + self.bias) * self.ope

class ED_Layer:
    def __init__(self, in_, out_, alpha=1., f=sigmoid):
        self.alpha = alpha
        self.f = f
        self.cells= ED_Linear(in_, out_)
    
    def __call__(self, x):
        return self.forward(x) 
        
    def forward(self, x):
        self.x = x
        self.y = self.f(self.cells(self.x))
        return self.y

    def update(self, d):
        db = np.einsum("b,pbo->pbo", d,  self.f.d(self.y))
        dw = np.einsum("pbo,qbi->pqbio", db, self.x)
        self.cells.weight += self.alpha * dw.mean(2)
        self.cells.bias += self.alpha * db.mean(1, keepdims=True)
   
class ED:
    def __init__(self, in_, hidden_width, hidden_depth=1, alpha=.8):
        self.layers = [
            ED_Layer(in_, hidden_width, alpha, sigmoid),
            *[ED_Layer(hidden_width, hidden_width, alpha, sigmoid) for _ in range(hidden_depth)],
            ED_Layer(hidden_width, 1, f=sigmoid)
        ]
    
    def __call__(self, x):
        return self.forward(x)
    
    def forward(self, x):
        x = x[None].repeat(2, 0)
        for layer in self.layers:
            x = layer(x)
        return x[0, :, 0]
    
    def update(self, d):
        for layer in self.layers:
            layer.update(d)

xor

np.random.seed(seed=1)
ed = ED(2, 8, 5)

data = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = data[:, 0] ^ data[:, 1]
for i in range(100):
    output = ed(data)
    d = y - output
    ed.update(d)
    
for i, j in [[0, 0], [0, 1], [1, 0], [1, 1]]:
    print(i^j, ed(np.array([[i, j]])))
    

おわりに

ED法の実装を通していろいろ課題点なども見えてきました。
これらの問題がどのように解決されていくのか、それとも不可避なED法の限界なのか、今後の発展が楽しみです。

ご本家

1. 正しくは$f'(i^k_j)$ですが、計算上出力値を使用することを強調している表記だと思われます。 ↩